El Tetris como mediador visual para el reconocimiento de movimientos rígidos en el plano (rotación y traslación)^*

Tetris as a visual mediator for the recognition of rigid movement on a plane (rotation and traslation)

Jenny Patricia Acevedo Rincón^**
Leonor Camargo Uribe^***

^*Una versión preliminar de este documento fue publicada en Acevedo y Camargo (2011).
^**Programa de Transformación de la Calidad Educativa del Ministerio de Educación Nacional. Bogotá, Colombia. jacevedo@minieducacion.gov.co.
^***Universidad Pedagógica Nacional. Bogotá, Colombia. leonor.camargo@gmail.com.

Recibido: 15/01/12, aprobado: 15/11/12

Resumen

El videojuego forma parte de la realidad de los jóvenes de la actualidad. En procura de aprovechar algunos beneficios del entorno visual del videojuego en el aula de matemáticas tales como: dinamizar la reflexión, desarrollar competencia de resolución de problemas y estimular capacidad deductiva, se desarrolló un proyecto de investigación que hace uso del videojuego en tareas de acercamiento a los conceptos geométricos de rotación y traslación. En este artículo presentamos un marco analítico para identificar procesos y habilidades de visualización que se desarrollan al aprovechar el videojuego como mediador visual y damos cuenta de un estudio investigativo a partir del cual ilustramos los efectos del uso del Tetris en la resolución de tareas desarrolladas por tres estudiantes con necesidades particulares de aprendizaje del Gimnasio Los Robles (Bogotá).

Palabras Clave Videojuego, rotación, traslación, necesidades educativas.

Abstract

The game is part of the reality of today's youth. In seeking to leverage some of the benefits of the visual environment of the game in the mathematics classroom such as dynamic reflections, develop problem-solving competition, stimulate deductive powers, developed a research project that uses video game to approach tasks geometric concepts of rotation and translation. In this lecture we present an analytical framework to identify processes and visualization skills are developed to exploit the game as visual mediator and realize a research study from which illustrate the effects of the use of Tetris in solving tasks performed by three students with particular learning needs of Gimnasio Los Robles (Bogotá).

Keywords Video game, rotation, translation, educational requirements.

Introducción

El Gimnasio Los Robles considera el modelo pedagógico de la modificabilidad estructural cognitiva (MEC) que impulsa el desarrollo de un conjunto de funciones intelectuales que sirven de soporte a ciertas acciones u operaciones con las que se resuelven situaciones problema. Las funciones y operaciones son de carácter general, por lo que no se discriminan acciones específicas asociadas a la comprensión y uso de conceptos y procedimientos matemáticos, hecho que dificulta poner en funcionamiento el modelo sugerido por el colegio, en esta asignatura. Este hecho nos condujo a desarrollar un proyecto de investigación tendiente a seleccionar, redefinir y caracterizar, a partir del análisis de las actuaciones de estudiantes, algunas funciones y operaciones del modelo que consideramos propias de la actividad geométrica y, particularmente, aquellas asociadas a habilidades y procesos de visualización.

En este artículo damos cuenta de un marco analítico para argumentar sobre los procesos y habilidades de visualización que se estimulan con el uso del videojuego Tetris. Este marco fue construido a partir de la selección de algunas categorías de visualización sugeridas en la literatura de referencia. Además, presentamos algunos resultados de una investigación que buscaba aprovechar dichos procesos y habilidades de visualización en una aproximación metodológica que pretende acercar intuitivamente a estudiantes, con necesidades particulares de aprendizaje, a los conceptos de rotación y traslación. Ilustramos, con ejemplos, el análisis realizado a algunos extractos de interacciones entre la profesora y un estudiante de quinto grado de primaria. Por último, presentamos unas reflexiones frente al trabajo investigativo desarrollado.

Procesos y habilidades de visualización

Partimos de la definición de visualización sugerida por Gal y Linchevski (2010) quienes la conciben como el conjunto de habilidades y procesos necesarios para representar, transformar, generalizar, comunicar y documentar información visual o reflexionar sobre ella. Según estos autores, la visualización interviene en tres momentos del proceso cognitivo: en la organización, o momento inicial de captura de información por medio de los sentidos; en el reconocimiento, o momento de aprovechamiento de la información visual en el trabajo cognitivo propiamente dicho; y de representación de información, o momento de comunicar los resultados del funcionamiento mental. A partir de estos momentos organizamos procesos y habilidades de visualización sugeridos por Presmeg (1986), Duval (1995), Bishop (1983) y Del Grande (1990), los cuales se constituyeron en categorías de análisis del estudio investigativo que adelantamos.

En el momento de organización ubicamos las siguientes habilidades sugeridas por Del Grande (1990), las cuales definimos y ejemplificamos con datos obtenidos en nuestro estudio.

Coordinación óculo-manual

Es la habilidad para seguir con los ojos el movimiento de los objetos de forma ágil y eficaz. Por ejemplo, en el uso del videojuego Tetris, esta habilidad se ve cuando los estudiantes logran coordinar los controles del juego (representados por flechas) y los movimientos propios del mismo; por ejemplo, ↑: giro de 90º, →: desplazamiento a la derecha.

Identificación visual

Es la habilidad para reconocer una figura aislándola de su contexto. El estudiante centra la atención en la figura, sin distraerse con estímulos irrelevantes. Por ejemplo, al jugar Tetris, los estudiantes centran la atención en la ficha que va bajando por el tablero del juego para poder ubicarla adecuadamente en el tablero, y olvidan por un momento la ficha siguiente o los elementos distractores del entorno.

Conservación de la percepción

Es la habilidad para reconocer que un objeto tiene propiedades invariables como forma y tamaño, a pesar de la variabilidad dada por el movimiento. Por ejemplo, al jugar Tetris, los estudiantes reconocen que las fichas están compuestas por configuraciones iguales de cuatro cuadros de igual tamaño, y que el movimiento de giro o desplazamiento no cambia ni la forma ni el tamaño.

Reconocimiento de posiciones espaciales

Es la habilidad para relacionar la posición de un objeto con uno mismo, es decir el observador. Por ejemplo, decimos que un estudiante tiene esta habilidad cuando logra identificar que una ficha se ha desplazado hacia la derecha o izquierda de la pantalla, según la posición del jugador.

Reconocimiento de relaciones espaciales

Es la habilidad que permite identificar correctamente las características de relaciones entre diversos objetos situados en el espacio. Por ejemplo, en Tetris, el estudiante es capaz de identificar los giros y desplazamientos necesarios para hacer encajar la ficha en un determinado espacio del tablero, e incluso, es capaz de predecir que la ficha que va bajando en el tablero y la futura ficha, pueden unirse para encajar en una determinada posición del tablero.

Discriminación visual

Es la habilidad que permite comparar dos o más objetos identificando sus semejanzas y diferencias. Por ejemplo, esta habilidad es evidente cuando los estudiantes son capaces de comparar un espacio del tablero con la configuración de una ficha en particular, estableciendo si la configuración es igual o no.

Memoria visual

Es la habilidad para recordar las características visuales y de posición que tenía un conjunto de objetos que estaba a la vista, pero que ya no se ve o que ha sido cambiado de posición. Por ejemplo, cuando los estudiantes son capaces de proponer fichas que podrían llenar un espacio en particular, a partir de su configuración, en caso de no tenerlas presentes y puede recordar la dirección de los giros de las fichas.

En el momento de reconocimiento, ubicamos dos tipos de aprehensiones definidas por Duval (1995) y los procesos de visualización señalados por Bishop (1983). Duval (1995) hace mención a la identificación visual de las figuras a partir de leyes de organización perceptiva, y que, a su vez, se pueden usar para representar objetos reales u objetos matemáticos. Plantea tres tipos de funciones cognitivas, que denomina como aprehensiones de las cuales solo hacemos referencia a la aprehensión operativa y la aprehensión discursiva, pues son las que usamos en los análisis.

Aprehensión operativa

Se produce cuando el sujeto lleva a cabo alguna modificación a la configuración inicial para resolver un problema geométrico y recuerda propiedades, movimientos y estrategias para llevar a cabo una tarea propuesta. Por ejemplo, en el caso particular del videojuego Tetris, los estudiantes son capaces de organizar un conjunto de estrategias para ponerlas en práctica a la hora de completar líneas del juego.

Aprehensión discursiva

Se produce cuando hay una asociación de una configuración con afirmaciones matemáticas (definiciones, teoremas, axiomas). Por ejemplo, cuando un estudiante es capaz de codificar y decodificar el lenguaje que le plantea el videojuego haciendo asociaciones geométricas con los controles. Además, el estudiante es capaz de expresar y argumentar sus propias ideas para resolver la situación planteada.

Por su parte, Bishop (1983) se refiere a dos procesos: interpretación de la información figural (IFI) y procesamiento visual (VP), ambos se incluyen en el momento de reconocimiento.

Interpretación de la información figural (IFI)

Es el proceso de interpretación de representaciones visuales para extraer información de ellas. Para que haya IFI debe existir un referente físico, de esta forma el individuo puede empezar a hacer el respectivo análisis. Por ejemplo cuando los estudiantes se enfrentan al problema de escoger el camino más óptimo para llegar a un espacio señalado en el tablero, son capaces de interpretar y argumentar sobre la información que extraen para decidir cómo hacer líneas y ganar más puntos en el juego.

Procesamiento visual (VP)

Es el proceso de conversión de la información no figurativa en imágenes visuales o transformación de unas imágenes visuales ya formadas en otras. Por ejemplo, cuando un estudiante es capaz de interpretar si una ficha que está bajando en el tablero, encaja en un espacio señalado el tablero.

En el momento de representación, ubicamos los tipos de imágenes men-tales sugeridos por Presmeg (1986), entendidas como las escenas mentales que describen información visual o espacial de un objeto sin requerir su presencia u otra representación externa. Presmeg diferencia tipos de imágenes con las que un individuo puede interactuar en una situación, de las cuales nosotros solo presentamos dos: cinéticas y dinámicas.

Imágenes cinéticas

Son imágenes en parte físicas y en parte mentales, ya que en ellas tiene un papel muy importante el movimiento de manos, cabeza, etcétera. En nuestro estudio, estas imágenes se hacen evidentes cuando los estudiantes quieren expresar el giro de un objeto que tienen en su mente y señalan con sus manos, u otra parte de su cuerpo o con un objeto externo a su cuerpo, como la ficha del Tetris, la dirección de esta rotación.

Imágenes dinámicas

Son imágenes mentales en las que los objetos o algunos de sus elementos se desplazan. Estas imágenes se aprecian cuando un estudiante está interactuando con imágenes del videojuego Tetris y predice los movimientos; estas predicciones corresponden a imágenes de su mente que están en movimiento.

Un acercamiento intuitivo a la rotación y la traslación

En la investigación consideramos un acercamiento intuitivo a la rotación y la traslación. Por eso resaltamos el potencial de las habilidades y procesos de visualización en el reconocimiento de algunas propiedades matemáticas de dichas isometrías. Nuestro acercamiento tiene las siguientes características:

Aproximación visual

A partir de figuras geométricas que muestran el giro o desplazamiento de una figura referenciada, las posiciones que ocupa en un plano (tablero de Tetris), las posiciones relativas al observador (o jugador), y las relaciones de las figuras entre sí, con el objeto de cumplir una tarea (ganar el juego).

Acercamiento por invariantes

En el caso de la rotación, los estudiantes deben reconocer giros de 90º en un mismo sentido y deben asociar los giros a efectos producidos por el control ↑del juego. En las traslaciones, los estudiantes deben reconocer los desplazamientos en tres direcciones: derecha (→), izquierda (←) y abajo (↓). Deben poder reconocer que, en el caso de experimentar una rotación, las figuras mantienen la forma y el tamaño pero cambian de orientación; en cambio, en el caso de experimentar una traslación, las figuras mantienen la forma, el tamaño y la orientación, pero su posición varía.

Uso de vocabulario informal

Asociamos la palabra girar con el movimiento de rotación y las palabras correr, bajar o mover con el movimiento de traslación.

Además, cuando los estudiantes mencionan "cambio", aceptamos que se están refiriendo, en general, al uso de uno de los movimientos rígidos en el plano, o a la combinación de ellos.

Metodología investigativa

A continuación se describen las variables que influyeron en el análisis de las categorías descritas en el estudio.

Contexto del estudio

El estudio fue realizado en el Gimnasio Los Robles, que atiende a niños con dificultades de aprendizaje o emocionales, y otros que no las tienen. Al ingresar al Gimnasio, los estudiantes adelantan sus estudios en una enseñanza regular, mientras van superando o compensando sus dificultades, si las tienen, gracias al acompañamiento interdisciplinar constante que les brinda el Gimnasio. Los estudiantes partícipes del presente estudio tienen dificultades de aprendizaje y/o emocionales. El modelo de enseñanza y aprendizaje utilizado en dicha institución corresponde a la modificabilidad estructural cognitiva (MEC). En este modelo se parte del diagnóstico de las disfunciones de los estudiantes para darle a cada uno el tratamiento adecuado, y brindarle el apoyo para que las disfunciones sean superadas durante su estadía en el Gimnasio. Las disfunciones diagnosticadas al ingresar al colegio se agrupan de acuerdo con cada una de las fases de enseñanza del modelo:

Entrada: percepción borrosa, comportamiento asistemático, vocabulario reducido, desorientación espacial, desorientación temporal, problemas para establecer lo esencial, recopilación de datos imprecisa, consideración de menos de dos fuentes de información.

Elaboración: no percibe el problema, no distingue datos, no tiene conducta comparativa, escasa amplitud del campo mental, percepción episódica, no hay razonamiento lógico, no hay interiorización del propio comportamiento, dificultad para proponer hipótesis lógicas, incapacidad de verificación de hipótesis, conducta por ensayo y error, dificultad para elaborar categorías cognitivas, reducción de la conducta sumativa, dificultad para establecer relaciones.

Salida: conducta egocéntrica, no establece relaciones virtuales, bloqueo en la comunicación, respuestas por ensayo y error, uso de instrumentos verbales inadecuadas, poca exactitud en la comunicación de repuestas, deficiencia en el transporte visual, conducta impulsiva.

Después de hacer el diagnóstico de las disfunciones cognitivas, se prevé lograr una modificabilidad de tipo cognitivo, en la medida en que la mediación hecha por los docentes sea favorable para el aprendizaje de los estudiantes. Dentro del aula de clases, la modificabilidad se logra a partir de proyectos que contemplan potenciar operaciones mentales durante el desarrollo del mismo en cada una de las áreas. Generalmente, dichos proyectos son semestrales para los grados de preescolar a quinto, y anuales para los grados de sexto a undécimo. Aunque la gran mayoría de las operaciones men-tales son trabajadas por medio de la interacción en el aula, solo se propone potenciar una o dos de ellas a lo largo de un proyecto de aula desarrollado en un contexto específico.

Las operaciones son activadas a través de funciones que se trabajan de acuerdo con las especificidades de las áreas. El desarrollo de cada proyecto de aula contempla por lo menos dos situaciones problemas semestrales, que llevan a proponer pequeñas situaciones que conllevan al desarrollo de funciones específicas del área. Al finalizar cada bimestre, se evalúan los conceptos trabajados teniendo en cuenta el proyecto de aula de cada grado. Y al finalizar cada semestre, los estudiantes dan muestras de sus aprendizajes por medio de la exposición de los productos realizados a lo largo del proyecto.

Los estudiantes

El estudio investigativo se llevó a cabo con nueve niños con edades entre 9 y 12 años, quienes cursaban quinto primaria durante el año 2010. Para efectos del análisis de las manifestaciones, se tomó en cuenta solo la tercera parte de la población. Para escoger los tres niños se tuvieron en cuenta las historias individuales (concepto diagnóstico), en donde se recogió el desempeño que tenía cada estudiante al ingresar al Gimnasio Los Robles. Los estudiantes eran: Juan David, Miguel Ángel y José Daniel. A continuación, para ilustrar el perfil de los niños, mostramos una breve descripción del diagnóstico realizado a Juan David, hecho por los terapeutas de la institución:

Juan David ingresa al colegio a los 9 años. Se caracteriza por su comportamiento hiperactivo, con dificultades para: fijar, mantener y distribuir la atención, clasificar elementos de acuerdo con atributos comunes, comprender y resolver situaciones problema sencillas, así como analizar y sintetizar información. Se observa buen desempeño en control oculomotor, fijación y seguimiento visual, respeto de límites, uniformidad y direccionalidad, además de buenas habilidades de percepción visual (figura-fondo, constancia perceptual, relaciones espaciales y análisis y síntesis visual). Se observa aceptable memoria y buena motivación. Al momento de participar en el presente estudio, Juan David tenía 13 años.

Etapas de la investigación

Etapa 1: Selección del videojuego Tetris

Escogimos el videojuego Tetris, tipo puzzle, que con sencillos movimientos y fácil uso de los controles, permite un acercamiento a los movimientos rígidos en el plano: rotación y traslación. Gracias a su entorno visual, fortalece el acercamiento intuitivo a nociones matemáticas contribuyendo a la construcción del significado de estas. Como lo indica Sedeño (2000), la componente visual de un videojuego favorece el control psicomotriz, la coordinación ojo-mano, el desarrollo de espacialidad; ayuda a dinamizar la reflexión sobre las causas y consecuencias de acciones; estimula la capacidad deductiva, la competencia en resolución de problemas, la imaginación, la memoria y las habilidades de análisis y síntesis.

Etapa 2: Selección de los estudiantes para el estudio de caso

Estudiamos las carpetas diagnósticas, con la debida autorización de la institución. En ellas reconocimos, en cada uno de los estudiantes, las dificultades y fortalezas que daban muestras de un perfil cognitivo de cada estudiante. De esta manera, escogimos al grado quinto B, de la sección primaria, para realizar el estudio de caso. Este curso contaba con nueve estudiantes con necesidades particulares de aprendizaje.

Etapa 3: Diseño de la secuencia didáctica

Hicimos el diseño de una secuencia didáctica para el acercamiento a las nociones de rotación y traslación, a partir de la articulación de operaciones y funciones del modelo de modificabilidad estructural cognitiva (MEC) y los procesos y habilidades de visualización seleccionados. Cada una de las actividades planteadas da cuenta de la activación de funciones a favor del desarrollo de las operaciones mentales.

Etapa 4: Toma de datos investigativos

Después de hacer las debidas adaptaciones de la secuencia didáctica, en cuanto a tiempo de aplicación y disponibilidad horaria, procedimos a la aplicación del mismo teniendo en cuenta el uso del videojuego. Las grabaciones se hicieron por miembros del personal de la institución y de la docente investigadora de este proyecto. Las actividades se desarrollaron en el salón de clases y la sala de informática.

Etapa 5: Transcripción de los videos y selección de los estudiantes para el estudio de caso

Posterior a la toma de datos, se hizo la transcripción de los nueve videos para iniciar su respectiva interpretación. Vale la pena aclarar que aunque se hizo la transcripción de los nueve videos, la interpretación y el análisis minucioso de cada manifestación solo se hizo a tres de los nueve estudiantes grabados, ya que no se contaba con el tiempo disponible para realizar el análisis de los seis estudiantes restantes.

Etapa 6: Selección de los fragmentos para el análisis

Las intervenciones de los estudiantes eran extensas, por lo que se vio conveniente segmentar las intervenciones de cada uno, transcribirlas en orden cronológico y realizar el respectivo análisis, atendiendo a las necesidades del proyecto en cuanto al desempeño frente a las funciones y operaciones del modelo de modificabilidad estructural cognitiva (MEC) que se constituyeron en las categorías específicas de análisis. Por ejemplo, de Juan David se tienen 29 manifestaciones.

Etapa 7: Identificación de manifestaciones exitosas y no exitosas de los estudiantes

La selección que hicimos de las manifestaciones de los estudiantes nos permitió la identificación de aquellas en las que los estudiantes se mostraban exitosos

o no, con el fin de contrastar su desempeño con la información obtenida del diagnóstico que hicieron las terapeutas del colegio y con el comportamiento en clases de matemáticas.

Etapa 8: Síntesis de las manifestaciones y perfil cognitivo de los estudiantes

Procedimos a hacer la respectiva síntesis de cada uno de los estudios de casos, en los que evidenciamos una ruta cognitiva utilizada por los estudiantes para acercarse a las nociones de rotación y traslación.

Secuencia didáctica

En la secuencia didáctica prevista en el estudio, se propusieron actividades organizadas en tres momentos: presentación del juego, interacción con el videojuego y prueba escrita. A continuación, se describen algunas de ellas. La descripción detallada de las actividades puede consultarse en Acevedo (2010).

Momento 1: Presentación del juego

Se presenta el videojuego a los estudiantes, las fichas que se usan, y los posibles movimientos y desplazamientos de éstas sin que ellos interactúen directamente con el videojuego. Se muestra a los estudiantes modelos de cada una de las siete fichas del Tetris, elaborados en foamy¹ de diferentes colores; se invita a los estudiantes a nombrarlas de acuerdo con formas familiares de letras y figuras geométricas (te, ele, jota, zeta, ese, i y cuadrado), y reconocer sus subconfiguraciones de cuadrados de igual tamaño unidos por los lados. Adicionalmente, se establecen semejanzas y diferencias entre las figuras, se comparan aquellas que son imagen bajo una reflexión de otras fichas como la ele con la jota, y la ese con la zeta.

Se muestran otras figuras hechas en foamy de formas y tamaños diferentes a las del Tetris, mostradas inicialmente, para que los estudiantes discriminen cuáles pertenecen al conjunto de las fichas del videojuego. Con modelos de fichas hechas en foamy de color blanco, que pertenecen a Tetris, los estudiantes seleccionan aquella ficha que es igual a una sugerida por la profesora, la ubican en un tablero de corcho fijándola con chinches y hacen rotaciones de 90º para establecer las posibles posiciones diferentes en las que pueden ubicarse.

Es claro que en este momento de la secuencia, no es posible evidenciar comportamientos de estrategia e hipótesis para actuar ante situaciones determinadas porque no hay interacción con el videojuego, por consiguiente se plantea el momento 2.

Momento 2: Interacción con el videojuego

Los estudiantes interactúan con el videojuego y conversan con el profesor. Se hacen preguntas sobre lo que el estudiante ve en un momento determinado. Al hacer las preguntas, los estudiantes deben haber descubierto las herramientas "pausa" y "reinicio" del juego, ya que estas son un apoyo para controlar el movimiento de las fichas. En este momento es preciso verificar la orientación espacial eficiente, conservación de la percepción, aprehensión operativa y tratamiento de estrategias para verificar hipótesis; de igual manera, se considera apropiado evaluar el razonamiento divergente de los estudiantes a partir de errores cometidos intencionalmente.

Momento 3: Prueba escrita

Se diseña una prueba escrita con preguntas sobre algunas situaciones planteadas en el videojuego. Estas permiten observar si el estudiante decodifica los movimientos a realizar en el plano de la hoja de papel. También se pregunta sobre estrategias a usar, cómo evaluar los errores cometidos en ciertas jugadas, describir fichas que tiene y plantear estrategias para cumplir con el objetivo, entre otras.

Análisis

A manera de ilustración de los análisis realizados, presentamos dos extractos de conversaciones con el estudiante Juan David en las fases de entrada y de elaboración de la secuencia.

Ejemplo 1 (fase de entrada)

El siguiente extracto de conversación está sacado de una interacción con el estudiante, en la fase de entrada e ilustra la manera como Juan David, se refiere a las características de la configuración de las fichas que no pertenecen al videojuego Tetris, por medio de interpretación de la información figural.

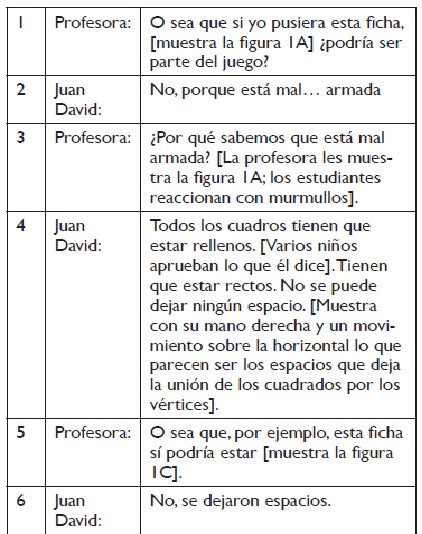
La profesora muestra al grupo de estudiantes la representación de una figura compuesta por cuatro cuadrados de igual tamaño, pero unidos por los vértices, formando una cadena. Su intención es que los estudiantes reconozcan que las fichas del Tetris están formadas por cuatro cuadrados de igual tamaño que están unidos por los lados. Después de mostrar la ilustración, la profesora les pregunta a los estudiantes si la figura puede ser parte del juego. Responden varios estudiante al tiempo, pero la voz de Juan David se diferencia de las demás, a pesar de no ser el directamente interrogado.

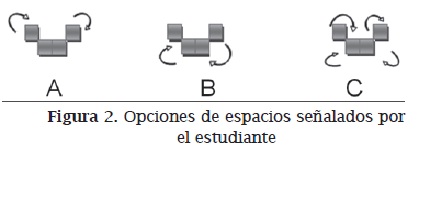
En un primer momento, Juan David reconoce que una figura no tiene la configuración de las fichas del Tetris y se refiere a ella como "mal armada" [2]. Identifica visualmente la diferencia que existe entre las fichas del Tetris y la figura que se muestra. A petición de la profesora, argumenta por qué no es una ficha del Tetris. Para ello se refiere a que no se pueden dejar espacios [6] y explica a qué se refiere con la expresión "los cuadros tienen que estar rellenos" [7]; entonces hace la comparación y posiblemente imagina los cuadros en teselado formando una figura, para diferenciar las figuras del Tetris con la que se le muestra, pero no usa el vocabulario adecuado para hacer la explicación. Para confirmar que el estudiante se refiere a los espacios que dejan los cuadrados cuando se unen por los vértices, la profesora muestra otra figura con una configuración similar. Efectivamente, el estudiante responde que se siguen dejando espacios y lo confirma ante la insistencia de la profesora [8-13]. Finalmente, ella muestra una figura del Tetris que Juan David reconoce como correcta [15]. Andrés, un compañero explica que los cuadrados se unen por los lados, expresando con claridad lo que Juan David estaba tratando de decir, y Juan David asiente.

El desempeño en la tarea confirma que Juan David interpreta la configuración patrón de las fichas del Tetris, pero no hace uso del vocabulario adecuado ya que lo que es más evidente es la dificultad de estudiantes para comunicar lo que está pensando en relación con la operación identificar.

Juan David lleva a cabo la operación de identificación por medio de interpretación de la información figural, aunque no expresa sus ideas de manera adecuada, en la medida en que el estudiante logra extraer características generales de la ficha que no pertenece al Tetris, la compara con las fichas que sí pertenecen desde el referente físico mostrado en el tablero. El hecho de reconocer la configuración de la ficha está muy relacionado con los invariantes; se mantiene la forma y tamaño, en el caso de la rotación, y en traslación se conservan forma, tamaño y orientación.

Frente al uso del videojuego, la manifestación muestra cómo el estudiante hace reflexionar al estudiante y estimula su capacidad deductiva para reconocer las características de la configuración de las fichas que pertenecen o no al videojuego Tetris.

Ejemplo 2 (fase de elaboración)

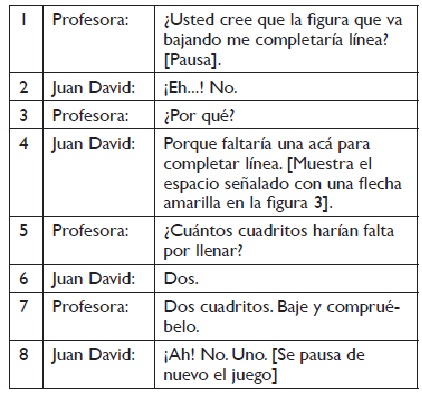
El siguiente fragmento de conversación está sacado de una interacción con el estudiante, en la fase de elaboración de la propuesta de enseñanza para analizar el proceso de aprehensión operativa. Con las fichas en movimiento, la profesora pregunta si las fichas que van bajando por el tablero llenan el espacio que se muestra y si, además, completan alguna línea.

Al realizar una comparación de la ficha que va bajando con el espacio que se debe llenar, Juan David presupone que la ficha no llena el espacio y afirma que se necesitan dos cuadros para llenarlo; sin embargo, al compararlo se da cuenta que hace falta solo un espacio.

La respuesta que da Juan David, a partir de una medición que hace a "ojo", corresponde a una hipótesis errada que plantea para después verificar utilizando los controles [2-8]. Esto nos permite ver que Juan David da muestras de poner en juego la función "tratamiento de estrategias para verificar hipótesis", sin tener éxito en el desarrollo de la tarea. De lo anterior podemos concluir que el estudiante no logra una aprehensión operativa, pues aunque tiene presente la jugada, no logra reunir una o un grupo de estrategias adecuadas para llegar a la solución de la situación.

Aunque el efecto del videojuego en esta situación no sea positivo, dicho ejemplo sirve para ilustrar como el estudiante se apropia de la situación para dar solución a la misma. Esto es, el estudiante logra poner en juego competencia de resolución de problemas, mediante el uso de estrategias o hipótesis planteadas y aunque son erradas, él logra darse cuenta de esto posteriormente con la solución del mismo.

El análisis de las interacciones de Juan David con el videojuego y con la profesora nos permitió identificar un cambio en el perfil cognitivo, por lo menos circunstancial. A diferencia del diagnóstico realizado por los terapeutas de la institución, se pudo observar que mediante el desarrollo de la secuencia didáctica se logró que el estudiante superara algunas de sus dificultades frente a aspectos puntuales como concentración y comunicación. A continuación mostraremos la síntesis de los resultados exitosos y no exitosos de Juan David durante el estudio de caso:

• Frente a la identificación, el estudiante logra reconocer las fichas, relacionarlas con letras y formas geométricas. Encuentra el lado, que es importante al reconocer invariabilidad de la forma por transformación. Recompone una figura a partir de la rotación y traslación de fichas
• Frente a los movimientos rígidos en el plano, hace la rotación de las fichas concretas. Identifica giros y desplazamientos. Relaciona espacios y fichas, a través de rotación y traslación hechas a las mismas. Usa la rotación y la traslación para hacer coincidir una pareja de fichas en un espacio. Percibe el efecto de una transformación en las fichas en movimiento. Relaciona la rotación y traslación con giros y desplazamientos respectivamente, y estos con los controles del juego. Utiliza la composición de rotación y traslación.
• Frente a las estrategias y pensamiento divergente, Juan David anticipa estrategias en términos de las jugadas más rápidas. Además, reconoce el error justificando la posible jugada en términos de composición de movimientos de rotación y traslación

Lo que se puede justificar, en la mayoría de manifestaciones, es que Juan David es un estudiante que se mantiene atento desde la presentación del juego hasta la prueba escrita. Ello manifiesta su falta de control sobre las respuestas que emite. El estudiante necesita frecuentemente de la ayuda de un estímulo externo -como señas, ayuda de los compañeros y de la profesora- para dar respuestas adecuadas; pues, aunque se acerca a las respuestas esperadas, no cuenta con un vocabulario fluido.

Es evidente que Juan David mantuvo una excelente coordinación ojo-mano, durante el momento del juego del Tetris.

Además, el estudiante logró controlar sus movimientos a partir del descubrimiento de la herramienta pausa para poder replantear lo que piensa y poder expresarlo. Su trabajo es constante durante la ejecución de las actividades, por lo que se puede evidenciar que mantuvo una adecuada motivación durante el trabajo con las actividades propuestas.

Por último, podemos ver que las manifestaciones no exitosas de Juan David radicaron en la falta de uso adecuado de vocabulario y en el comportamiento exploratorio sistemático, ya que él logró en el resto de tareas, un desempeño adecuado. Además, tuvo un acercamiento a los conceptos de rotación y traslación con nociones intuitivas y relacionadas con movimientos corporales. Por esto, encontramos posible que el estudiante entienda los efectos de dichos movimientos rígidos en el plano cuando dicho se enfrente a los temas en mención en el grado siguiente al que cursa actualmente.

Algunas reflexiones

Sobre el comportamiento de estudiantes con necesidades particulares de aprendizaje

El videojuego permite que los estudiantes del estudio muestren desempeños exitosos al desarrollar las tareas propuestas en la secuencia didáctica, en tareas que apuntan a la noción de traslación y rotación. La componente visual de la herramienta del Tetris logra centrar la atención y distribuirla para realizar adecuadamente tareas que implican movimientos rígidos en el plano, además de permitir la motivación del estudiante para que las estrategias que plantee le ayuden a ganar el juego. Esto implica que algunas de las dificultades de un estudiante con necesidades particulares de aprendizaje, sean compensadas con otras habilidades desarrolladas por él durante la actividad, al utilizar el recurso tecnológico.

Sobre el videojuego y el aprendizaje en matemáticas

Se puede observar que el videojuego Tetris, acompañado de un diseño pedagógico apropiado, favorece el desempeño en el acercamiento a las nociones matemáticas de niños que tienen necesidades particulares de aprendizaje frente a reflexión, desarrollo de competencias de resolución de problemas, y capacidad deductiva. Vale la pena resaltar que aunque existen diferentes tipos de videojuegos que son llamativos por su entorno visual, y de sumo interés para los estudiantes, no todos ofrecen el entorno necesario para tratar con conceptos matemáticos sencillos.

Sobre el manejo de grupo en la implementación de estas actividades

Es muy probable que el uso de este tipo de actividades en grupos grandes no dé resultados positivos, ya que la preparación y aplicación de las mismas demandan tiempo y atención constante en cada uno de los "videojugadores".

Pie de página

¹También llamado goma Eva, que por su flexibilidad permite la fácil manipulación del juego en concreto.

Referencias

Acevedo, J. (2010). Modificabilidad estructural cognitiva vs. Visualización: un ejercicio de análisis del uso del Tetris en tareas de rotación y traslación. Tesis de maestría. Bogotá: Universidad Pedagógica Nacional.         [ Links ]

Acevedo, J. y Camargo, L. (2011). El Tetris como mediador visual para el reconocimiento de movimientos rígidos en el plano (rotación y traslación). En: Memorias del XX Encuentro de Geometría y sus Aplicaciones (pp. 333-345). Bogotá: Universidad Pedagógica Nacional.         [ Links ]

Bishop, A. (1983). Spatial abilities and mathematical thinking. En: M. Zweng; T. Green; J. Kilpatrick; H. Pollak y M. Suydam (eds.). Proceedings of the Fourth International Congress on Mathematical Education (pp. 176-178). Boston, EE.UU.: Birkhauser.         [ Links ]

Del Grande, J. (1990). Spatial sense. Arithmetic Teacher, 37(6), 14-20.         [ Links ]

Duval, R. (1995). Geometrical pictures: Kinds of representation and specific processings. En: R. Sutherland y J. Mason (eds.). Exploiting mental imagery with computer in mathematics education (pp. 142-158). Berlín, Heidelberg: Springer-Verlag. Consultado el 16 de junio de 2010 en: http://books.google.com/books?id=R6PC8GCt2ACampprintsec=frontcoverdq=Computersas_brr=3cd=90source=gbs_slider_thumb#v=onepageqf=false.         [ Links ]

Gal, H. y Linchevski, L. (2010). To see or not to see: analyzing difficulties in Geometry from the perspective of visual perception. Educational Study of Mathematics, 74, 163-183 DOI 10.1007/s10649-010-9232-y. Online Springer Science+BusinessMedia B.V. 2010.         [ Links ]

Presmeg, N. (1986). Visualization in High School mathematics. For the learning of mathematics, 6(3), 42-46.         [ Links ]

Sedeño, A. (2002). La componente visual del videojuego como herramienta educativa. En: Revista Iberoamericana de Educación (ed.). Recuperado el 10 de octubre de 2011 de www.rieoei.org/deloslectores/308sedeno.pdf        [ Links ]