La relación entre educación matemática, democracia y adolescencia

Comenzamos por parafrasear a Dussel para señalar que es desde la historicidad desde donde podemos comprender la relación entre educación matemática, democracia y adolescencia. Inés ^{Dussel (2006)} señala que en muchos países de la región latinoamericana, más significativamente en los del Cono Sur, la educación para la democracia desempeñó un papel fundamental en la constitución de una sociedad civil. Las etapas de "democratización" de los sistemas escolares latinoamericanos corresponden a la aparición de nuevos discursos con los que la escuela enfrentaría a los "nuevos públicos", especialmente generados por la "cultura joven". ^{Sáenz y Ariza (2012)} relatan que en el contexto colombiano, en la década de los años treinta, la visión sobre la vida de la adolescencia que circuló en los discursos estaba relacionada con el peligro moral y social propio de la adolescencia sustentada en representaciones procedentes de la biología, la pobreza y en conjeturas sobre las características de las poblaciones de las diferentes regiones del país (^{Sáenz, Ariza, 2012}).

La consecuencia para la escolarización de los jóvenes se centró en la necesidad de ampliación e intensificación disciplinaria de prácticas de regulación moral para que el adolescente lograse la cooperación y el encauzamiento de los comportamientos. Para Sáenz y Ariza, la escuela comenzó a constituir un saber para gobernar con formas específicas socializadoras a los adolescentes. ^{Duschatzky (2005)} recalca que históricamente la escuela constituyó este saber "en la imposibilidad de no ser y de no poder no ser: no puede hablarse de cualquier modo, no pueden los chicos desconcentrarse en la clase, no se puede no prestar atención" (2005, p. 2). Desde esta perspectiva, parecería que los problemas escolares de los jóvenes se establecen de antemano, los traen a la escuela lejos de localizarse en la estructura escolar. De aquí que ciertas apreciaciones sobre la cultura juvenil operen como recurso para justificar los comportamientos disruptivos de los estudiantes en el salón de clase.

En Colombia la ley general de educación (Ministerio de Educación Nacional, MEN, 1995) organizó la Educación Básica Secundaria con el propósito de fomentar en la institución educativa prácticas democráticas para el aprendizaje de los principios y valores de la participación y organización ciudadana y estimular la autonomía y la responsabilidad. Demanda una educación matemática acorde a los requerimientos globales relacionados con una educación para todos y con la diversidad. Las instituciones educativas y la escolarización de las matemáticas son cruciales para alcanzar la "globalización de la cultura matemática" asociada con la creciente interconexión entre inclusión cultural y economía mundial. De estos principios se deriva un sistema de integración que, según parece, impone maneras unívocas de racionalidad inclusiva: matemáticas para todos que paradójicamente reitera la inclusión indiscriminada y homogeneizante que garantiza el progreso y la prosperidad de la sociedad en general.

Desde los aportes del giro social y los cambios en investigación en educación matemática se reconoce que los estudiantes llegan a participar en las prácticas del aula de matemáticas a partir de un conjunto individual de experiencias socioculturales (^{Lerman, 2000}) y que el aula se concibe como el espacio de manifestación de múltiples trayectorias individuales, cruzadas por los modos en que los estudiantes se quieren ver desarrollándose "quizá como el loco del aula, quizá como atractivo para alguien del aula, que no es el profesor" (2000, p. 33). ^{Planas (2003)} utiliza la metáfora Sur/Norte para visibilizar las diferencias que son encubiertas por los principios de objetividad del conocimiento matemático y la objetivación de los procesos cognitivos que encauzan la investigación sobre el aprendizaje de las matemáticas. Las diferencias en el estatus de los estudiantes dependen de factores que no son solo de orden cognitivo, sino que dependen de la cultura dominante del aula. Esta fija las normas de actuación en el aula, derivadas de la selección y organización del currículo. Desde estas organizaciones se establece qué es válido como práctica matemática escolar y qué no lo es. Lo que es visible en las tareas matemáticas, los procedimientos y criterios de evaluación. Las selecciones curriculares sobre los contenidos llevan implícita una selección de valores. No es lo mismo dar prioridad a la enseñanza estructural de las matemáticas para avanza hacia los estudios universitarios, que priorizar la resolución de problemas relacionados con la vida cotidiana de los estudiantes (Planas, 2003).

Sin lugar a dudas, Umbiratan D' Ambrossio con la etnomatemática puso en cuestión la idea de una identidad común con un único patrón de la racionalidad de la matemática. Desde la etnomatemática, Knijnik (1996), Knijnik, Wandere y Oliveira (2005) han cuestionado la política del conocimiento dominante practicada en la escuela, marcada por las desigualdades y discriminación de manifestaciones culturales distintas al racionalismo matemático que caracteriza el conocimiento matemático escolar. Estos investigadores llaman la atención para referirse a las matemáticas en plural como "artefactos culturales directamente conectados con instituciones, con las tradiciones, con maneras de vivir, de sentir y de producción de significados de los diferentes grupos sociales" (2012, p. 15).

Valero y ^{Skovsmose (2012)} consideran necesario impulsar una democracia cultural con las matemáticas sobre la cual se pueden sostener las esferas políticas y económicas de la democracia para cerrar el círculo de desigualdad cultural producido por el uso de las competencias matemáticas "como un filtro social para tener acceso al éxito futuro" (2012, p. 30). Sin embargo, lo cultural y su carácter constitutivo en los terrenos social y político son procesos que requieren ser revisados críticamente a la luz de las nuevas formas de generación de conocimientos matemático en distintas actividades humanas y donde se activan múltiples relaciones entre saberes y disciplinas Estos autores proponen que la idea de democracia se constituye en las relaciones sociales entre la personas, es decir, porque comparten valores, acciones como el respeto, la igualdad, la responsabilidad social, el interés y la actuación coordinada con los otros miembros de la comunidad.

Construcción de la diversidad y valoraciones

Comenzaremos por señalar que en las investigaciones¹ realizadas el foco de estudio han sido las transformaciones del dispositivo de escolarización de las matemáticas en las relaciones entre las dimensiones epistemológicas del eje del conocimiento matemático y el eje de constitución de las nuevas subjetividades juveniles. Al estudiar las distintas reformas curriculares en Colombia con las matemáticas, adelantadas desde la década de los noventa, encontramos en los principales postulados que organizan los conocimientos matemáticos el cierre del tamiz de las matemáticas escolares a la circulación de otros saberes. Valero y ^{Skovsmose (2012)} consideran que desde el punto de vista cultural es posible relacionar "las ideas matemáticas con el empoderamiento de la gente en relación a sus condiciones de vida". Puesto que el estudio de situaciones problemáticas en la vida de los estudiantes puede iniciar cambios en su participación, en ellas se encuentran saberes cercanos a la vida social, política y económica de los estudiantes. En estos saberes, las matemáticas se esconden tras estructuras y rutinas sociales que tienen contenidos matemáticos relevantes desde una perspectiva del contenido del aprendizaje, de la importancia sociológica de aprender en la escuela, y de la posición misma de los niños.

Escenarios de aprendizaje de las matemáticas: herramienta teórica y metodológica

Poner de relieve el estudio de las conexiones entre la valoración personal y los procesos de valoración de las prácticas matemáticas en el aula pone en relación dos nociones: cultura y diversidad. ^{AlrØ, Skovmose y Valero (2005)} proponen la noción de escenarios de aprendizaje, como una herramienta teórica y metodológica que configura la complejidad de un escenario donde el aprendizaje y las prácticas matemáticas están representadas en escenarios de diversidad cultural. La noción tiene un doble significado: en primer lugar, representa una interpretación de la educación matemática como una red compleja de práctica social constituida por diferentes dimensiones interrelacionadas. En segundo lugar, como herramienta metodológica, hace posible identificar dimensiones específicas e interdependientes de los diferentes componentes de prácticas de educación matemática que tienen un impacto en la forma en que el aprendizaje y la enseñanza tienen lugar en el aula, donde los procesos de exclusión son evidentes. El montaje de cada escenario relaciona dimensiones relevantes que la investigación reciente ha identificado para una mejor comprensión de la complejidad social y política que constituye las aulas de matemáticas. La interacción entre las dimensiones y los contextos escolares donde se montan los escenarios configuran la cultura de la clase, y el foco de la mirada se desplaza del sujeto a las prácticas educativas con las matemáticas.

La identificación de las dimensiones en cada montaje de un escenario incluye una microetnografía de la cultura de la clase de matemáticas. Mediante la observación participante, el análisis documental de los currículos, de los planes de evaluación y de actividades de los estudiantes comprendimos que la cultura de la clase de matemáticas esta constituida por la estratificación, es decir, el ordenamiento y la clasificación de los estudiantes de acuerdo con sus habilidades matemáticas para obtener el éxito del aprendizaje. Debido a las políticas que buscan facilitar el acceso a la educación secundaria, las aulas se poblaron de adolescentes con distintas experiencias, con distintos conocimientos, valores, intereses, motivaciones, interpretaciones del mundo y con experiencias educativas distintas; "portadores" de ciertas "culturas". Para una gran mayoría de profesores de matemáticas en las aulas de secundaria es preocupante encontrar cada vez con mayor frecuencia en las clases un número considerable de estudiantes/adolescentes que no tiene interés alguno en participar en las actividades de aprendizaje y con actitudes de rechazo que se manifiestan en la indiferencia, en modalidades de resistencia o en el ausentismo. En la mayoría de los casos, las valoraciones de los comportamientos de los jóvenes se privatizan y se mezclan con tesis culturales relacionadas con modos de vida y maneras de ser de lo juvenil. De manera general podemos decir que las microetnografías nos han aportado al reconocimiento del lugar prominente que ocupan los estudiantes como agentes sociales en la clase por la diversidad de valoraciones y legitimidades que circulan en el aula.

El montaje de los escenarios "No le des la espalda a tu espalda" y "Cuánta agua gastamos" ilustra la utilidad de la noción cuando el aprendizaje de las matemáticas se da en contextos de diversidad cultural. La cultura de la clase de matemáticas se asume con un único patrón de racionalidad de las matemáticas que se evidencia en la objetivación de la adquisición de los contenidos matemáticos expresados en habilidades o competencias matemáticas que promueven la homogeneidad y al mismo tiempo la estratificación como un principio establecido por las valoraciones sobre habilidades matemáticas y roles sociales de los estudiantes. Los escenarios buscan generar en las dinámicas de las prácticas educativas interacciones sociales constituidas por el respeto, la igualdad, el interés y la responsabilidad social. Estos principios nos permiten enfocarnos en el arraigo de valores democráticos en la clase, visibilizados en las dimensiones seleccionadas como constitutivas de los escenarios: (1) participación colectiva de los estudiantes, determinada por un sentido de igualdad en las interacciones dialógicas entre estudiantes y estudiantes y profesor, (2) contextualización y tematización del contenido matemático desde la perspectiva cultural de los estudiantes y con el propósito de que estos se vinculen a las actividades propuestas desde diversas habilidades (^{Powell, 2002}), (3) descentralización y desgeometrización del currículo (^{Knijnik, Wanderer, Giongo y Duarte, 2012}), (4) los recursos de que se dispone para el proceso educativo con las matemáticas, (e) la interacción dialógica entre alumnos y entre alumnos y profesor en el aula. De esta manera buscamos que las prácticas educativas que se basan en los escenarios incluyan los motivos para las acciones de los estudiantes y su vinculación a las actividades que componen cada escena. En dichas teorizaciones e interpretaciones ha prevalecido la idea de enfatizar en el papel de la cultura de la clase para crear y dar lugar a la constitución de intersubjetividades dialógicas. Es cierto que en el contexto de la clase de matemáticas se espera que los estudiantes se adhieran a normas y valores definidos en las prácticas escolares con las matemáticas y que se identifiquen con esta cultura. Pero también es cierto que en la clase de matemáticas coexisten diferentes actividades en las que diferentes grupos participan (^{Lerman, 2000}). La formación de diferentes grupos culturales está relacionada con las dinámicas colectivas en esa clase. La pertenencia a un grupo cultural alrededor de habilidades matemáticas o de comportamientos sociales, por ejemplo, demarca procesos de estar dentro o fuera, lo que produce condiciones diferentes para que los estudiantes experimenten situaciones de aprendizaje con las matemáticas (^{Alr0, Skovsmose y Valero, 2005}). El montaje y desarrollo de cada escenario estuvo a cargo de una profesora, estudiante de la maestría en Docencia de la Matemática. Cada escenario está conformado por una serie de escenas caracterizadas por actividades cuya solución requiere de soluciones colectivas mediadas por las interacciones de los participantes asociadas a la modelación matemática. Para seguir el desarrollo de cada escena utilizamos la observación no participante, la grabación en video y los registros escritos de los estudiantes. En la grabación de los videos los registros se enfocaron en las interacciones entre los equipos. Luego procedimos a transcribir las grabaciones. La unidad de análisis correspondió a cada una de las escenas. Siguiendo a Skovmose (1999), en la sistematización utilizamos la modalidad de narrar fotografías, entendida como modo de "leer" cómo las diferentes dimensiones permiten una interpretación interdependiente de las dimensiones en las prácticas educativas como un todo.

No le des la espalda a tu espalda

El curso 903 está localizado en una institución pública que tiene como objetivo formar a los estudiantes para el acceso a la educación superior. El porvenir, para la mayoría de ellos, se relaciona con ir a la universidad y viajar por el mundo. El colegio es reconocido por los niveles obtenidos en las pruebas externas de calidad y porque la mayoría de estudiantes acceden a las universidades. Gran parte de los 36 estudiantes de la clase han construido su biografía escolar en el colegio.

En la clase de matemáticas, los estudiantes trabajan de forma individual, y en los momentos de trabajo en grupos se organizan de acuerdo a sus habilidades matemáticas. La modalidad de evaluación repercute en los ambientes de aprendizaje de las matemáticas y provee una estratificación de los estudiantes; los de mayor prestigio en sus habilidades matemáticas siempre son los que tienen la autoridad. Esto se evidencia en la forma como se organizan para realizar las actividades propuestas por el profesor: los reconocidos por sus altas habilidades matemáticas prefieren trabajar solos.

Los estudiantes continuamente se quejaban por el sobrepeso de sus maletas escolares, que se asociaba al día en que transportaban más textos escolares, y aunque tenían los textos de cada asignatura, muchos preferían traer copias a las clases. La problemática del peso excesivo de la maleta escolar ha demandado investigaciones que han mostrado médicamente que el sobrepeso de la maleta escolar puede generar a corto y largo plazo serios problemas en la salud de la espalda de los estudiantes. Por tal razón, se ha convertido en fuente de campañas de prevención al inicio del año escolar en los medios de comunicación.

Sobre la base de las ideas expuestas montamos el escenario "No le des la espalda a tu espalda", con el objetivo de cambiar la cultura de la clase de matemáticas al integrar una problemática social y culturalmente relevante para los estudiantes (descentralizar el currículo de la materia). Nos propusimos desarrollar acciones centrándonos en los procesos de colectividad (Valero y ^{Skovsmose, 2012}) entendidas como acciones propositivas para analizar/solucionar el problema. Una cuestión importante en el escenario es la integración del cuidado del cuerpo, puesto que buscábamos que los estudiantes comprendieran que lo que le pasa al cuerpo, su malestar, es malestar del sujeto. Las matemáticas escolares involucradas en el escenario están relacionadas con prácticas de medición y relaciones funcionales de dependencia.

¿Cuánta agua gastamos?

El montaje del escenario se llevó a cabo en una institución pública ubicada en la zona urbana del municipio de Cajicá (39 km al norte de Bogotá, la capital de Colombia), zona caracterizada por la siembra y comercialización de flores y de productos agrícolas y derivados de los lácteos. Las fuentes hidrográficas del municipio no son abundantes, por tal motivo debe comprar el agua a las empresas públicas de Bogotá, lo que genera el alto costo en los recibos y su mal servicio. Esta situación estaba convocando a la comunidad para aportar a la solución. Con el escenario "¿Cuánta agua gastamos?" nos propusimos darle sentido educativo a las matemáticas para contribuir a buscar soluciones a esta situación.

En el curso 701, las edades de los estudiantes varía entre los 11 y 17 años; algunos son repitentes.

Escena 2. Calcular cuánta agua gastamos

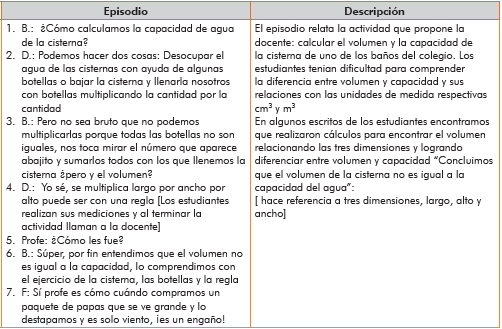
En esta escena, a partir de la pregunta "¿Cuánta agua gastamos?" buscamos que los estudiantes modelaran con los conceptos de volumen y capacidad, los datos recolectados, para estimar la cantidad de agua consumida en la institución educativa y en sus casas. En la escena precedente hacen cálculos y algunos errores conducen a discusiones entre saberes aritméticos relacionados con la multiplicación. El siguiente episodio (tabla 1) identifica un acercamiento a procesos de coflexión en los que se evidencian diálogos entre estudiantes.

Tabla 1 Episodio de interacción de procesos de coflexión y deliberación. 

Fuente: Navarrete (2015).

Podemos mencionar que los procesos de participación colectiva y deliberación no se dan de manera inmediata, requieren de un proceso en el que intervienen múltiples e interrelacionados factores como: el tipo de tareas y las preguntas, de contar con las habilidades matemáticas para participar colectivamente en la solución de actividades matemáticas; del profesor para gestionar la participación de los estudiantes, de los tiempos curriculares fijados para el aprendizaje del uso de herramientas, etc. Aunque en las actividades de aprendizaje que se montaron en los escenarios se buscó relacionar los factores descritos, surgen las tensiones relacionadas con el estatus, la estratificación social en relación con la variable rendimiento académico, los lazos de amistad y las emociones.

Finalmente, también es necesario destacar que la red conceptual asociada al escenario relaciona actividades del pensamiento numérico (uso de números racionales en sus distintas representaciones), la justificación de cálculos en la solución de problemas con el pensamiento espacial (representación y caracterización de objetos tridimensionales) y con el pensamiento métrico (cálculo e interpretación de volumen de sólidos, estimación, relaciones entre distintas unidades, uso de unidades de medida estandarizadas), y el pensamiento variaciones (representación de situaciones de variación, proporcionalidad directa) y pensamiento aleatorio (organización e interpretación de datos, tablas de frecuencias, gráficas estadísticas, medidas de tendencia central).