ARTÍCULO DE INVESTIGACIÓN / RESEARCH ARTICLE

Modelo para la planificación en la cadena de suministro:
Selección y asignación a proveedores en el caso de lotes fijos

A model for supply chain planning:
Supplier selection and quantity allocation in the case of fixed lot size

Alex J. Ruiz Torres*
Universidad de Puerto Rico, Recinto de Río Piedras (Puerto Rico)

Abraham Mendoza**
Universidad Panamericana, Campus Guadalajara (México)

José Humberto Ablanedo Rosas***
University of Texas at El Paso (USA)

* Director Interno alex.ruiztorres@upr.edu

** Director. amendoza@up.edu.mx

*** Profesor Asistente. jablanedorosas2@utep.edu

Correspondencia: José Humberto Ablanedo Rosas, University of Texas at El Paso, Information and Decision Sciences Department, 500 W University Avenue, El Paso, TX 79968 (USA). Tel.: 1 915 747 6041. Fax: 1 915 747 5126. jablanedorosas2@utep.edu.

Resumen

La globalización de los sistemas de producción ha llevado a las organizaciones a considerar la gestión de proveedores como una decisión estratégica. Existen una gran cantidad de investigaciones sobre la toma de decisiones relacionadas con la administración de los sistemas de aprovisionamiento y selección de proveedores. Sin embargo, la investigación en el caso de múltiples proveedores con diferentes características y atributos, que deben satisfacer una demanda con lotes de insumos de tamaño fijo es limitada. La demanda de este tipo es particular en algunos esquemas de producción por procesos, como es el caso de la industria alimentaria y farmacéutica. El objetivo de este artículo es llenar este vacío de investigación en la gestión de proveedores. La metodología empleada se basa en el desarrollo de un modelo de Programación Lineal Entera Mixta que optimiza la decisión de selección y asignación a proveedores en el caso de lotes fijos. La solución de un ejemplo numérico comprueba la aplicabilidad y utilidad del modelo. Además, se presenta un análisis de sensibilidad del modelo, realizando diferentes cambios en algunos de sus parámetros y se demuestra su sensibilidad a los diferentes escenarios. Los resultados muestran que el modelo es práctico y puede ser replicado fácilmente por organizaciones que compran sus insumos en lotes de tamaño predeterminado.

Palabras clave: Asignación a proveedores, gestión de proveedores, modelos de decisión, órdenes por lote de tamaño fijo, planeación de la cadena de suministro, selección de proveedores.

Abstract

The globalization of production systems has led organizations to consider the supplier management function as a strategic decision. There is signifcant research work addressing decision making and supplier management. However, there is a lack of research in the case of multiple suppliers with different characteristics and attributes and able to satisfy a product demand defined by a fixed lot size. This kind of demand arises in production environments organized by processes such as the pharmaceutical and food industry. This research aims at fulfilling this lack of research in supplier management. The proposed methodology is based on the formulation of a Mixed Integer Linear Programming model for optimizing the decisions of supplier selection and order quantity allocation in the case of fixed lot size. A numerical example shows the applicability and usefulness of the proposed model. Furthermore, a sensitivity analysis shows that the model is sensitive to changes in parameters. Finally, the results also show that the model is practical and can be easily adapted by organizations that purchase products in fixed-size lots.

Keywords: Decision making models, order allocation with fixed lot size, supplier management, supplier selection, supply chain planning, supply quantity allocation.

El surgimiento y desarrollo de organizaciones interdependientes y la expansión de la globalización en los sistemas de producción ha llevado a las empresas de una gran variedad de industrias a prestar una mayor atención a la función de aprovisionamiento [1]. En particular, la literatura sobre la toma de decisiones relacionada con proveedores sigue creciendo hoy en día, dada su relevancia para productores y distribuidores que componen las cadenas globales de suministro. Seleccionar proveedores y asignar los requerimientos de insumos entre ellos es un proceso crítico para la mejora de la competitividad empresarial mediante el logro de altos niveles de servicio al cliente en combinación con costos bajos [2], [3].

Para alcanzar los objetivos de servicio al cliente en combinación con costos bajos, las compañías se concentran en el desarrollo de pocos proveedores como socios estratégicos para facilitar la colaboración desde la etapa de diseño hasta la entrega, a fin de reducir los costos del producto y mantener una excelente calidad y servicio al cliente [1], [2]. Aún así, en la mayoría de los casos, para garantizar la confiabilidad del flujo de aprovisionamiento, se utiliza una política de proveedores múltiples. Además, integrar la planeación de órdenes de compra con la selección de proveedores puede generar ahorros significativos, dados los diferentes costos correlacionados en el proceso. Al considerar un horizonte de varios períodos, uno o más proveedores pueden ser seleccionados en cada período y se tiene en cuenta que los inventarios pueden ser acarreados a períodos futuros. La mayoría de los modelos propuestos en la literatura tratan el problema de selección de proveedores sin considerar tales aspectos [1].

Aunque la mayoría de los estudios previos consideran la selección de proveedores para un producto, sólo algunos modelos consideran la compra de un lote de productos simultáneamente [1]. En la práctica, por lo general, los proveedores se utilizan para múltiples productos que pertenecen a una misma familia o tipo de tecnología. Por ejemplo, una organización podría usar el mismo proveedor (o un grupo pequeño de proveedores) para muchos de sus ingredientes químicos, y usar otro proveedor (o un grupo pequeño de proveedores) para la mayoría de sus piezas moldeadas de plástico. Además, con frecuencia se usan varios proveedores de acuerdo al volumen de demanda y tratando de disminuir los riesgos, o al menos estos deben ser considerados durante el proceso de decisión. Así, si uno o más proveedores no pueden proporcionar todas las partes requeridas, el resto de los proveedores pudieran hacerlo, evitando problemas de abastecimiento. De hecho, es muy arriesgado tener un sólo proveedor proporcionando un insumo crítico.

A pesar de la importancia de la selección de proveedores y la cantidad de insumos asignados a cada proveedor, el problema no ha sido suficientemente abordado en la literatura [2], [4]. Es un problema complejo que envuelve factores cuantitativos y cualitativos. Por lo tanto, algunos investigadores han propuesto enfoques híbridos al integrar diferentes métodos de solución del problema (por ejemplo [5]). Además, la mayoría de los estudios previos consideran un solo período de tiempo y no incorporan el tamaño del lote en el modelo de decisión. Las tres decisiones más importantes en la selección y asignación a proveedores son: qué insumos (productos) pedir, las cantidades de insumos por proveedor y en qué período de tiempo.

Esta investigación tiene como objetivo abordar la decisión de compra de insumos considerando la selección de proveedores y la asignación de cantidades de insumos entre proveedores. La organización necesita varios tipos de insumos, que puede obtener de un grupo de proveedores. Se supone que cada proveedor puede producir al menos un subconjunto de los diferentes tipos de insumos requeridos. Los insumos a comprar sólo se entregan en cantidades predeterminadas, y la cantidad es particular para cada uno de los proveedores. Los proveedores venden cada artículo a un precio único y tienen una determinada capacidad para cada período de tiempo. La demanda de la organización que compra varía con el tiempo, por lo que el problema asume un horizonte con múltiples períodos de tiempo. Asimismo, los costos asociados con la gestión de proveedores se consideran en función de un período de tiempo. La organización puede tener material en inventario y puede retrasar la compra de artículos, lo cual podría incurrir en un costo adicional por retrasos en la entrega de pedidos (backorder). Por lo tanto, nuestro modelo considera tanto el costo de mantener inventario como el costo de producción que se pierde por falta de insumos para realizarla.

Este problema se observa en la industria de procesos; en particular, la que produce alimentos y medicinas, que tiene tamaños predefinidos de lote para insumos. Porque la cantidad de insumos a comprar está definida con base en recetas, muchas veces "pre-certificadas" por agencias gubernamentales y no pueden ser fácilmente transformadas para lotes más pequeños o más grandes; o el equipo utilizado está diseñado para manejar determinados tamaños de lote, en este caso el uso de lotes más pequeños daría lugar a bajos rendimientos de producción. Aunque este es un problema de importancia significativa para la industria, hasta ahora no ha sido abordado por la literatura científica.

El artículo se desarrolla de la siguiente manera: Sección 2 Selección y asignación de proveedores en la literatura previa. Sección 3, descripción del problema. Sección 4, ilustra un ejemplo numérico. Y en la Sección 5 se presentan las conclusiones e implicaciones en la gestión de proveedores.

La literatura en el área de selección y asignación a proveedores ha crecido exponencialmente en los últimos cinco años. Esta revisión toma trabajos recientes en el área, incluyendo algunas cuestiones abordadas, características de los problemas y modelos desarrollados. Aissaoui et al. [1] describen investigaciones que analizan la selección de proveedores empleando la investigación operativa y los modelos computacionales, describen las características de los modelos de decisión principales y proponen diferentes clasificaciones de los modelos publicados. Sarache Castro et al. [6] analizan la literatura y establecen que la construcción de una política adecuada de selección de proveedores debe tomar en consideración al menos tres argumentos: (1) el análisis del contexto y las particularidades de la cadena de abastecimiento, (2) la estrategia para la función de aprovisionamiento y los criterios de decisión y (3) los métodos de selección como apoyo a la decisión. El trabajo realizado por Ho et al. [7] revisa la literatura sobre la toma de decisiones que considera criterios múltiples para la evaluación y selección de proveedores.

Los trabajos recientes sobre la selección y asignación a proveedores con frecuencia se enfocan en el desarrollo de modelos que capturan las variables del proceso de toma de decisiones y se orientan a la asignación de pesos e importancia a estas variables. Culverweell et al. [8] investigan un modelo cuantitativo para la evaluación y selección de proveedores en el caso de la industria minera chilena. Sarache et al. [9] aplican técnicas multi-criterio para evaluar proveedores en una empresa colombiana del sector metalmecánico. Amid et al. [10] desarrollan un modelo lineal que pretende superar las disyuntivas relacionadas con los criterios de selección. El modelo utiliza una técnica asimétrica que permite al tomador de decisiones asignar diferentes pesos a varios criterios. Kim et al. [11] asumen la perspectiva de proveedor sobre los criterios de selección y proponen un marco basado en la coincidencia entre la capacidad del proveedor y las necesidades de tercerización (outsourcing), para mantener relaciones sostenibles entre proveedores y compradores. Hasan et al. [12] abordan el diseño y la im-plementación de un procedimiento para evaluar proveedores de organizaciones de manufactura ágil. La investigación se centra en determinar los factores cuantitativos y cualitativos apropiados que se pueden usar para evaluar y seleccionar proveedores que se ajusten y adecuen a las prácticas ágiles de la organización. García Alcaráz et al. [13] presentan un modelo de optimización multi-objetivo que integra costo, servicio, confiabilidad, administración, organización y tecnología, como atributos en el proceso de decisión. Osorio et al. [14] plantean una metodología multi-criterio para la selección de proveedores de una empresa manufacturera colombiana, utilizando el despliegue de la función de calidad difusa como herramienta para la toma de decisiones. El modelo contempla las necesidades y expectativas del comprador y considera como elemento fundamental del proceso el conocimiento que tiene la compañía tanto de los materiales y procesos, como de los proveedores candidatos a ser seleccionados.

Varios autores han usado el Proceso Analítico Jerárquico (PAJ) en modelos que apoyan la selección de proveedores y el proceso de toma de decisiones en la asignación. Herrera Umaña y Osorio Gómez [15] desarrollan un sistema PAJ difuso para resolver el problema de decisión multi-criterio asociado con la gestión de proveedores e implementan el modelo en una empresa colombiana con resultados satisfactorios. Moynihan et al. [16] presentan un modelo PAJ de decisiones para asistir en las funciones de adquisición y selección del proveedor. El modelo evalúa a los proveedores con base en ciertos factores como el costo, tiempo de entrega, ubicación (distancia) del proveedor y un score de desempeño. Rajan et al. [17] combinan el PAJ con un análisis de las utilidades por producto para evaluar y seleccionar un grupo de proveedores para un conjunto de productos con respecto a una priorización de los productos y a las expectativas de los clientes; el resultado es un proveedor con un producto asignado. Levary [18] describe cómo un enfoque basado en el PAJ fue usado para evaluar proveedores extranjeros en un caso industrial real. Osorio Gómez et al. [19] aplican PAJ para evaluar proveedores en una empresa de servicios en Colombia. Ting y Cho [20] combinan el PAJ con un modelo de programación lineal multi-objetivo para asignar cantidades de pedido a los proveedores, mientras que Ozgen et al. [21] combinan un modelo probabilístico lineal multi-objetivo para el mismo problema. Yu y Tsai [22] proponen un modelo que integra el PAJ con programación entera para asignar una calificación y ordenar, en función de esta calificación, a los proveedores. Luego el modelo es usado para asignar compras periódicas a los proveedores. Mendoza y Ventura [23] proponen un método de doble fase que combina el PAJ con un modelo de inventario entero mixto no lineal para seleccionar un conjunto de proveedores.

El Proceso Analítico Sistémico (PAS) es otro método usado recientemente por varios investigadores. En el trabajo de Ustun y Demirtas [24] el PAS se utiliza para determinar la importancia de los criterios asociados con un proveedor, y luego esta información es utilizada en un modelo de programación lineal entera mixta multi-objetivo para generar un conjunto de soluciones eficientes. Los tomadores de decisiones se involucran en este proceso de desarrollo del modelo mediante la selección de sus soluciones preferidas, y esta información se utiliza para ajustar los parámetros del modelo. Razmi y Rafiei [25] utilizan un modelo PAS para calificar proveedores y filtrar los candidatos adecuados entre los disponibles. Lin [26] combina el PAS con programación preferente difusa para generar los pesos de la función objetivo, que luego son utilizados en un programa multi-objetivo lineal para generar asignaciones óptimas.

Múltiples enfoques se han propuesto para resolver el problema de la priorización y captura del proceso de decisión dentro de una organización de compras. Sanayei et al. [5] combinan la teoría de utilidad con múltiples atributos y la programación lineal para resolver el problema de la asignación al proveedor. Rezaei y Davoodi [27] desarrollaron un algoritmo genético para resolver el caso de proveedores con productos de calidad defectuosa, donde los elementos imperfectos se venden a un precio con descuento. Azadeh et al. [28] combinan análisis envolvente y difuso de datos con un programa lineal entero multi-objetivo para asignar una cantidad óptima de pedido a los proveedores. Che y Wang [29] consideran el caso de elementos comunes que se utilizan en los productos finales múltiples, presentan una formulación matemática para ese entorno y un algoritmo genético para resolverla. Ustun y Demirtas [30] y Wu et al. [31] consideran el problema de asignación del proveedor desde un punto de vista múltiple, tomando en cuenta el costo total, la calidad en la forma de una tasa de defectos o tasa de rechazo, valor y servicio al cliente. Estos últimos proponen un modelo basado en programación lineal multi-objetivo difusa, y demuestran en su enfoque la sensibilidad de la solución al riesgo de la entidad que compra.

Varios autores se han ocupado de casos relacionados a descuentos de precio [2], [3], [32], [35]. Stadler [32] considera el problema de un descuento para todas las unidades y el caso de un descuento incremental, presenta un modelo de programación lineal entera mixta para resolver ambos casos. Xia y Wu [3] consideran el caso donde el descuento está basado en el volumen de la compra total asignada al proveedor, y proponen un enfoque compuesto por PAJ mejorado a través de la teoría de conjuntos aproximados y programación lineal entera mixta multi-objetivo. Burke et al. [33] consideran tres esquemas de descuento ofrecidos por los proveedores (por ejemplo, lineal, unidades incrementales y todas las unidades), y proponen una heurística para cada caso. Burke et al. [34] proponen una heurística limitada para el caso de la unidad incremental que eficientemente encuentra la solución óptima. Wang y Yang [35] combinan PAJ y programación lineal comprometida difusa para hacer frente a la naturaleza no heterogénea de la decisión. Sawik [2] considera los descuentos por volumen de compras para la asignación de los pedidos entre proveedores en un ambiente de manufactura que produce por órdenes. El problema también considera tasas de defecto y entregas tardías, los cuales son luego incluidos en las formulaciones individuales y multi-objetivos.

La variabilidad de la demanda y el desempeño de los proveedores también ha sido un tema de interés entre los investigadores. Yang et al. [36] consideran el caso de rendimientos aleatorios de los proveedores y una demanda variable. Xu y Nozick [37] abordan el tema del trastorno de la capacidad de entrega y lo formulan como un problema de ubicación de las instalaciones y de flujo de red con el objetivo de elegir un conjunto de proveedores que minimicen el total de los costos previstos. Los contratos de opción son utilizados para protegerse contra la pérdida de un proveedor, frente a la disyuntiva de los objetivos contrapuestos de minimizar riesgos y costos.

Yu et al. [38] también consideran los riesgos de interrupción de suministro y evalúan la decisión basada en el valor de la ganancia estimada. Shin et al. [39] proponen un modelo probabilístico de costos que toma en cuenta tanto la calidad como el desempeño en las entregas de los proveedores. Los autores prueban su modelo usando un caso industrial y concluyen que la contratación única es una estrategia efectiva en el caso de baja calidad con variabilidad.

Investigaciones recientes sobre selección de proveedores también han considerado la incertidumbre de la demanda, la generación de criterios duales de solución, y la consideración de los costos de transporte. Zhang y Ma [40] y Awasthi et al. [41] consideran el problema de selección de proveedores con incertidumbre en la demanda y donde cada proveedor tiene un precio único y una capacidad limitada. Zhang y Ma [40] presentan una formulación del problema basada en un modelo de programación no-lineal entera mixta, para definir políticas de contratación para uno o varios proveedores. Awasthi et al. [41] describen las características del problema, proponen un algoritmo de solución y evalúan el desempeño del algoritmo. Basnet y Weintraub [42] consideran el problema dual de minimizar el número de proveedores y los costos de adquisición. Ellos modelan el problema como un programa entero mixto en el cual cuestiones como calidad, demanda, capacidad y desempeño en la entrega son incorporados en forma de restricciones. Mendoza y Ventura [43] consideran el impacto del transporte tanto en la selección de proveedores como en las decisiones de reposición de inventarios. Los autores proponen un modelo de programación no lineal entera mixta para asignar correctamente las cantidades a ordenar a un grupo de proveedores seleccionados mientras se toman en cuenta los costos de adquisición, tenencia y transporte.

La revisión de la literatura ha sido clasificada de diferentes formas; desde la metodología utilizada para resolver el modelo propuesto hasta las suposiciones inherentes al modelo. Para el primer caso, identificamos diferentes técnicas tales como asignación de pesos a variables de decisión, programación matemática multi-objetivo, PAJ, PAS, y modelos de matemática difusa, por mencionar algunos de ellos. De manera similar, para el segundo caso se estudian diferentes suposiciones en los modelos propuestos entre las que podemos mencionar como ejemplo: descuentos por volúmenes de compra, incertidumbre y variabilidad de la demanda, variabilidad en el desempeño de proveedores y costos de transporte variables. Sin embargo, hay una falta de investigación para el caso de industrias que compran sus insumos en tamaños de lote predeterminados. Este artículo viene a cubrir este vacío y contribuye a la expansión del conocimiento en el área de administración de proveedores.

La metodología propuesta se basa en el desarrollo de un modelo de Programación Lineal Entera Mixta para optimizar la decisión de selección y asignación a proveedores en el caso de lotes fijos.

Descripción del problema

El modelo asume que s proveedores, S = {1...s}, están disponibles para suministrar los w tipos de artículos requeridos, W = {l...w}. El horizonte de planificación está definido por t períodos, T = {1...t}. Mientras que algunos proveedores pueden ser muy versátiles, es altamente probable que algunos proveedores solo puedan suministrar un subconjunto de W. S_k es el conjunto de proveedores que pueden producir y proporcionar el artículo k. Para que el artículo sea considerado como parte del modelo es necesario |S_k| > 1 o no habrá decisión que tomar (única fuente de opción). Mirando la misma situación del lado del proveedor, W_g es el conjunto de artículos que el proveedor g puede producir/entregar, pero en este caso |W_g| > 1, ya que si incluso el proveedor solo puede ofrecer uno de los artículos relevantes, este debería ser considerado en el proceso de toma de decisión.

Los proveedores producen lotes en cantidades predeterminadas, q_kg es el número de unidades por lote del artículo k del proveedor g. Cada lote de artículo k del proveedor g tiene un costo total de compra de c_kg que incluye el precio de venta del artículo, los costos de transporte y una cantidad de costos por procesamiento. Un proveedor g tiene una capacidad de producción para el período de tiempo z igual a p_gz. Esta descripción permite la variabilidad de la capacidad la cual puede representar la disponibilidad estacional, una causa de interés para los proveedores de alimentos. La capacidad utilizada por lote del artículo k del proveedor g se denomina u_kg, la variable d_kz representa la demanda total del artículo k en el período de tiempo z, la variable i_kz representa el nivel de inventario del artículo

k al final del período z, y la variable b_kz representa el nivel de inventario "negativo" del artículo k al final del período de tiempo z (por ejemplo, pedidos pendientes). El costo de mantener una unidad del artículo k por período de tiempo es h_k, mientras que v_k representa el costo de unidades pendientes por unidad por período para el artículo k. Asumimos que i_k0 y b_kg son el número inicial de unidades en inventario y el número inicial de unidades pendientes para el artículo k. La variable a_gz es una variable binaria que indica si el proveedor g se encuentra activo durante el período z, y m_g representa el costo de administración por tener al proveedor g como un proveedor activo durante un período de tiempo. Para algunos tipos de problemas esto podría ser considerado como un costo establecido. El objetivo del modelo es determinar el número de lotes x_kgz del artículo k a ser requerido de un proveedor g en el período de tiempo z el cual minimizará la retención de inventario, el inventario de pedidos pendientes, la cantidad de pedido, y los costos de gestión de proveedores. Finalmente se considera Φ como un número de magnitud muy grande, esto es Φ > Σ _{kεW z εT} d_kz. El siguiente modelo de programación lineal entera mixta sirve para representar el problema en análisis.

Formulación matemática del modelo

El objetivo de este modelo es minimizar los costos totales. Se definen los elementos de costo asociados a la planificación de proveedores como se indica a continuación:

Costos de inventario por artículo k, 

Costos de órdenes pendientes por artículo k,

Costos de adquisición por proveedor 

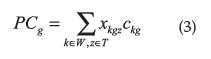
Costos de administración por proveedor g,

El objetivo es minimizar:

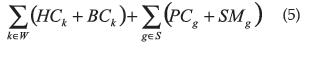
El modelo de selección de proveedor con lotes de tamaño pre-definidos y considerando la demanda variable, es el siguiente:

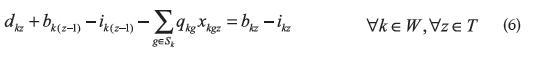
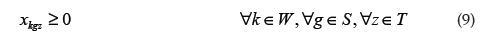
La función objetivo minimiza los costos de: mantener inventario, órdenes pendientes por recibir, compras y administración de proveedores (5). La restricción (6) es una condición de flujo de inventario regular para el artículo g tomando en cuenta todos los lotes recibidos del proveedor que puede producir el artículo k (S_k): la demanda para el período z más las órdenes del período previo se deben declarar en el inventario del período previo más todos los lotes recibidos durante el período z. La restricción (7) determina si un proveedor está activo o no durante el período en estudio. La restricción (8) limita los lotes asignados al proveedor g para todo el producto hasta el período z por la capacidad disponible total incluyendo el período z (e.g., p_gz). La restricción (9), (10) y (11) representan las variables enteras, binarias, y no negativas respectivamente. El modelo tiene w x t x s variables enteras y 2 t x s variables binarias.

La restricción de la capacidad solamente considera la disponibilidad de la capacidad por período de tiempo, no toma en cuenta el tiempo del proceso de producción dentro del horizonte de planificación. Por consiguiente, asume que la producción de un lote puede ocurrir en cualquier momento antes del período en estudio. Así, es posible que la producción ocurra bien antes de la demanda (y por ende la entrega del proveedor). Los costos asociados con la producción temprana (y por consiguiente los costos de inversión por el proveedor hasta el momento de la entrega) no están considerados en el modelo.

Esta sección presenta ejemplos numéricos para ilustrar las posibles aplicaciones del modelo propuesto para apoyar la asignación de proveedores. El ejemplo asume cuatro artículos a ser adquiridos en un horizonte de planificación de seis unidades (por ejemplo, w = 4, t = 6). Se consideran tres proveedores (por ejemplo, s = 3). La información del artículo incluyendo la inversión, las órdenes pendientes, la demanda y el conjunto de proveedores capaces se presenta en la tabla 1. La tabla 2 proporciona la capacidad de producción del proveedor por período de tiempo y los costos de administración. La tabla 3 proporciona toda la información relacionada a los proveedores; las unidades por lote, el costo de procesamiento por lote y la capacidad utilizada por cada lote.

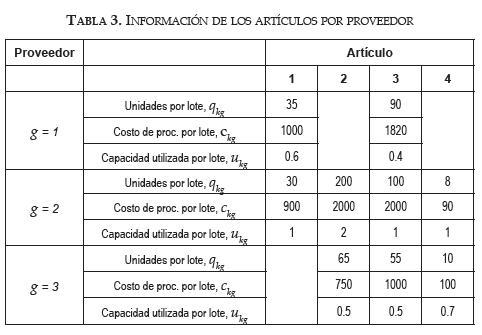
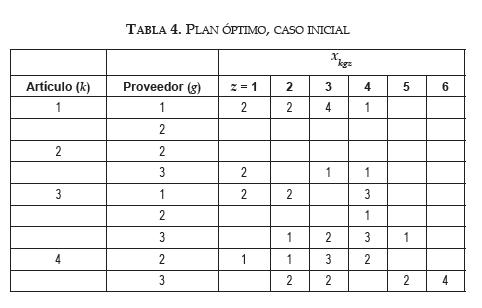
El ejemplo asume que el inventario inicial de artículos y las órdenes pendientes por recibir son 0. El modelo es resuelto usando el solucionador Excel/ Premium. La solución óptima a este ejemplo se presenta en la tabla 4. Los costos totales son $50,385 que se desglosan en $35,370 para compras, $1,025 para mantener inventario, $4,590 para órdenes pendientes por cumplir, y $9,400 para gastos de administración de proveedores. Los resultados presentados en la tabla 4 demuestran la capacidad del modelo para asignar la demanda entre proveedores, en algunos casos asigna toda la demanda de artículos a un solo proveedor (artículo 1 solo puede ser suministrado por el proveedor 1) o a todos los proveedores, o a través de todas las limitaciones de capacidad para determinado proveedor y las demandas de los diferentes artículos (artículo 3 comprado a tres proveedores).

Para ilustrar la sensibilidad del modelo a los cambios en los parámetros, en este estudio se agrega una unidad de capacidad al proveedor 3 en cada período de tiempo. El plan de asignación resultante se encuentra en la tabla 5. El nuevo costo total es $45,656, el cual se desglosa en $35,230 para compra, $976 para inventario, $1,250 para órdenes pendientes, y $8,200 para gastos de administración de proveedores. En esta situación donde la capacidad fue incrementada, algunas órdenes fueron combinadas (como por ejemplo en el artículo 3 donde el número de períodos con órdenes decrecieron en uno), y algunos proveedores fueron completamente eliminados del proceso de compra para algunos artículos (como por ejemplo el artículo 3, donde en el plan original el proveedor 2 recibió órdenes por 1 lote, pero en el plan enmendado no recibió órdenes).

Al comparar los resultados, los costos de inventario y compra están virtualmente invariados, mientras que los costos por órdenes pendientes y de administración de proveedores están reducidos. Este es un resultado esperado como la frecuencia de "ordenar" dada la reducción en los valores de las restricciones, resultando en menos órdenes en espera. Adicionalmente, un pequeño grupo de proveedores es usado, dando capacidad adicional al proveedor 3.

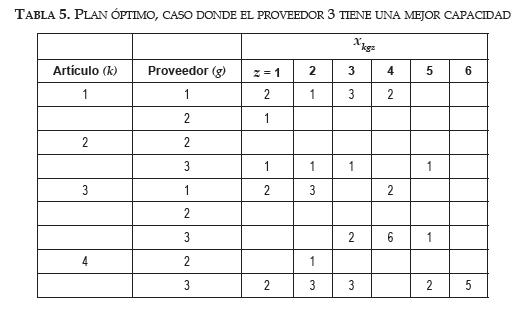
En el caso de mayor capacidad del proveedor 3, para el artículo 3, el proveedor 2 recibió órdenes por 7 lotes en el plan original y disminuyó a 1 lote en el plan enmendado. Las compras del proveedor 2 disminuyeron de $2,630 a $990. Como un segundo análisis de sensibilidad se considera el caso donde el proveedor 2 reduce el costo por lote de artículo 3 a $1700 (una reducción de $300 por lote) y se mantiene la condición de un nivel más alto de capacidad para el proveedor 3. El plan de producción se presenta en la tabla 6.

Como puede observarse, mientras el cambio solo se relaciona a un artículo y a un proveedor, éste tiene un efecto sobre los planes asociados con tres de los artículos, en particular para el proveedor 3 quien ahora no tiene asignado ningún lote de producción para el artículo 3 (todas las órdenes van a los proveedores 1 y 2). En este esquema el proveedor 2 es asociado a compras que totalizan $7,880 y el costo total es $44,773.

Este artículo presenta un modelo de selección y asignación a proveedores donde la producción ocurre en lotes de tamaño fijo. La organización de recursos requiere múltiples tipos de artículos que pueden ser suministrados por un grupo de proveedores, y asume que los proveedores del conjunto evaluado pueden producir una combinación de estos artículos. Los costos y las capacidades son función particular de cada proveedor y la demanda varía en el tiempo. El modelo considera los costos de mantener inventario, de pedidos atrasados, de administración de proveedores y de compra de insumos. La motivación para este modelo viene del proceso industrial en el cual un grupo de proveedores es utilizado para adquirir los insumos necesarios en lotes predeterminados de diferentes tamaños, restringidos por factores como la capacidad del tanque para la mezcla y la "receta" de producción aprobada por agencias gubernamentales.

Un ejemplo numérico es resuelto. El programa lineal mixto resultó ser útil para seleccionar y asignar órdenes a proveedores en diferentes períodos de tiempo. La solución óptima minimiza el costo total y proporciona la siguiente información por período de tiempo: unidades en inventario, órdenes pendientes de ser satisfechas, número de lotes por tipo de artículo a ser solicitados a cada proveedor e identifica los proveedores activos. Se realizó un análisis de sensibilidad al variar los valores de algunos parámetros en el modelo. Específicamente se analizó un incremento en la capacidad del proveedor y una disminución en el costo por lote de uno de los artículos. El modelo mostró ser sólido y altamente sensible a las variaciones en los parámetros al producir variaciones en la solución óptima ante los diferentes escenarios analizados.

El modelo propuesto es de uso general, práctico y sencillo de implementar, por lo que cualquier tipo de organización al enfrentar este tipo de situaciones lo puede incorporar fácilmente a sus procesos de toma de decisiones. Investigación futura incluye la incorporación de parámetros adicionales como pueden ser: tiempo de entrega y de producción de cada uno de los proveedores, descuentos por volúmenes de compra y confiabilidad de cada uno de los proveedores.

[1] N. Aissaoui, M. Haouari, and E. Hassini, "Supplier selection and order lot sizing modeling: A review," Comput. & Operations Research, vol. 34, pp. 3516-3540, 2007.         [ Links ]

[2] T. Sawik, "Single vs. multiple objective supplier selection in a make to order environment," Omega, vol. 38, pp. 203-212, 2010.         [ Links ]

[3] W. Xia and Z. Wu, "Supplier selection with multiple criteria in volume discount environments," Omega, vol. 35, pp. 494-504, 2007.         [ Links ]

[4] J. Razmi, M.J. Songhori, and M.H. Khakbaz, "An integrated fuzzy group decision making/fuzzy linear programming (FGDMLP) framework for supplier evaluation and order allocation," Int. J. of Advanced Manufacturing Technology, vol. 43, pp. 590-607, 2009.         [ Links ]

[5] A. Sanayei, S.F. Mousavi, M.R. Abdi, and A. Mohaghar, "An integrated group decision-making process for supplier selection and order allocation using multi-attribute utility theory and linear programming," J. of Franklin Inst., vol. 345, pp. 731-747, 2008.         [ Links ]

[6] W.A. Sarache Castro, O.D. Castrillón Gómez y L.F. Ortiz Franco, "Selección de proveedores: una aproximación al estado del arte," Cuadernos de Administración, vol. 22, pp. 145-167, 2009.         [ Links ]

[7] W. Ho, X. Xu, and P.K. Dey, "Multi-criteria decision making approaches for supplier evaluation and selection: A literature review," European J. of Operational Research, vol. 202, pp. 16-24, 2010.         [ Links ]

[8] M. Culverwell, M. Lufin Varas y G. Romni Chocce, "Estrategias de gestión de proveedores en la industria minera cuprífera de Chile," Rev. Venezolana de Gerencia, vol. 6, pp. 359-381, 2001.         [ Links ]

[9] W.A. Sarache, C. Hoyos Montoya y J.C. and Burbano J., "Procedimiento para la evaluación de proveedores mediante técnicas multicriterio," Scientia et Technica, vol. 24, pp. 219-224, 2004.         [ Links ]

[10] A. Amid, S.H. Ghodsypour, and C. O'Brien, "Fuzzy multi-objective linear model for supplier selection in a supply chain," Int. J. of Prod. Econ., vol. 104, pp. 394-407, 2006.         [ Links ]

[11] K.I. Kim, A.Y. Syamil, and B.J. Bhatt, "A resource-based theory of supplier strategy," Int. J. of Logistics Syst. and Manage., vol. 3, pp. 20-33, 2007.         [ Links ]

[12] M.A. Hasan, R. Shankar, and J. Sarkis, "Supplier selection in an agile manufacturing environment using Data Envelopment Analysis and Analytical Network Process," Int. J. of Logistics Syst. and Manage., vol. 4, pp. 523-550, 2008.         [ Links ]

[13] J.L. García Alcaráz, J. Romero González e I. Canales Valdivieso, "Selección de proveedores usando el método MOORA," CULCyT, vol. 7, pp. 40-41, 2010.         [ Links ]

[14] J.C. Osorio, D.C. Arango y C.E. Ruales, "Selección de proveedores usando el despliegue de la función de calidad difusa," Revista EIA, vol. 15, pp. 73-83, 2011.         [ Links ]

[15] M.F. Herrera Umaña y J.C. Osorio Gómez, "Modelo para la gestión de proveedores utilizando AHP difuso," Estudios Gerenciales, vol. 22, pp. 69-88, 2006.         [ Links ]

[16] G.P. Moynihan, P. Saxena, and D.J. Fonseca, "Development of a decision support system for procurement operations," Int. J. of Logistics Syst. and Manage., vol. 2, pp. 1-18, 2006        [ Links ]

[17] A.J. Rajan, K.S. Rao, and K. Ganesh, "VEPCE: decision-making model for vendor evaluation with respect to product prioritisation and customer expectation," Int. J. of Logistics Syst. and Manage., vol. 3, pp. 34-55, 2007.         [ Links ]

[18] R.R. Levary, "Using the analytic hierarchy process to rank foreign suppliers based on supply risks," Comput. & Ind. Eng., vol. 55, pp. 535-542, 2008.         [ Links ]

[19] J.C. Osorio Gómez, M.F. Herrera Umaña y M.A. Vinasco, "Modelo para la evaluación del desempeño de los proveedores utilizando AHP," Ingeniería & Desarrollo, vol. 23, pp. 43-58, 2008.         [ Links ]

[20] S-C. Ting and D.I. Cho, "An integrated approach for supplier selection and purchasing decisions," Supply Chain Manage.: An Int. J., vol. 13, pp. 116-127, 2008.         [ Links ]

[21] D. Ozgen, S. Onut, B. Gulsun, U.R. Tuzkaya, and G. Tuzkaya, "A two-phase possibilistic linear programming methodology for multi-objective supplier evaluation and order allocation problems," Inform. Sciences, vol. 178, pp. 485-500, 2008.         [ Links ]

[22] J. Yu and C. Tsai, "A decision framework for supplier rating and purchase allocation: A case in the semiconductor industry," Comput. & Ind. Eng., vol. 55, pp. 634-646, 2008.         [ Links ]

[23] A. Mendoza and J.A. Ventura, "An effective method to supplier selection and order quantity allocation," Int. J. of Bus. and Syst. Research, vol. 2, pp. 1-15, 2008.         [ Links ]

[24] O. Ustun and E.A. Demirtas, "Multi-period lot-sizing with supplier selection using achievement scalarizing functions," Comput. & Ind. Eng., vol. 54, pp. 918-931, 2008.         [ Links ]

[25] J. Razmi and H. Rafiei, "An integrated analytic network process with mixed-integer non-linear programming to supplier selection and order allocation," The Int. J. of Advanced Manufacturing Technology, vol. 49, pp. 1195-1208, 2010.         [ Links ]

[26] R. Lin, "An integrated FANP-MOLP for supplier evaluation and order allocation," Appl. Math. Modelling, vol. 33, pp. 2730-2736, 2009.         [ Links ]

[27] J. Rezaei and M. Davoodi, "A deterministic, multi-item inventory model with supplier selection and imperfect quality," Appl. Math. Modelling, vol. 32, pp. 2106-2116, 2009.         [ Links ]

[28] A. Azadeh, M.H. Khakbaz, and M.J. Songhori, "An Integrated framework for supplier evaluation and order allocation in a non-crisp environment," Int. J. of Logistics Syst. and Manage., vol. 6, pp. 76-98, 2010.         [ Links ]

[29] Z.H. Che and H.S. Wang, "Supplier selection and supply quantity allocation of common and non-common parts with multiple criteria under multiple products," Comput. & Ind. Eng., vol. 55, pp. 110-133, 2008.         [ Links ]

[30] O. Ustun and E.A. Demirtas, "An integrated multi-objective decision-making process for multi-period lot-sizing with Supplier Selection," Omega, vol. 36, pp. 509-521, 2008.         [ Links ]

[31] D.D. Wu, Y. Zhang, D. Wu, and D.L. Olson, "Fuzzy multi-objective programming for supplier selection and risk modeling: A possibility approach," European J. of Operational Research, vol. 200, pp. 774-787, 2010.         [ Links ]

[32] H. Stadtler, "A general quantity discount and supplier selection mixed integer programming model," OR Spectrum, vol. 29, pp. 723-744, 2007.         [ Links ]

[33] G.J. Burke, J. Carrillo, and A.J. Vakharia, "Heuristics for sourcing from multiple suppliers with alternative quantity discounts," European J. of Operational Research, vol. 186, pp. 317-329, 2008.         [ Links ]

[34] G.J. Burke, S.S. Erenguc, and A.J. Vakharia, "Optimal requirement allocation among quantity-discount quoting suppliers," Operations Manage. Research, vol. 1, pp. 53-60, 2008.         [ Links ]

[35] T. Wang and Y. Yang, "A fuzzy model for supplier selection in quantity discount environments," Expert Syst. with Applicat., vol. 36, pp. 12179-12187, 2009.         [ Links ]

[36] S. Yang, J. Yang, and L. Abdel-Malek, "Sourcing with random yields and stochastic demand: A newsvendor approach," Comput. & Operations Research, vol. 34, pp. 3682-3690, 2007.         [ Links ]

[37] N. Xu and L. Nozick, "Modeling supplier selection and the use of option contracts for global supply chain design," Comput. & Operations Research, vol. 36, pp. 2786-2800, 2009.         [ Links ]

[38] H. Yu, A.Z. Zeng, and L. Zhao, "Single or dual sourcing: decision-making in the presence of supply chain disruption risks," Omega, vol. 37, pp. 788-800, 2009.         [ Links ]

[39] H. Shin, W.C. Benton, and M. Jun, "Quantifying suppliers' product quality and delivery performance: A sourcing policy decision model," Comput. & Operations Research, vol. 36, pp. 2462-2471, 2009.         [ Links ]

[40] G. Zhang and L. Ma, "Optimal acquisition policy with quantity discounts and uncertain demands," Int. J. of Prod. Research, vol. 47, pp. 2409-2425, 2009.         [ Links ]

[41] A. Awasthi, S.S. Chauhan, S.K. Goyal, and J. Proth, "Supplier selection problem for a single manufacturing unit under stochastic demand," Int. J. of Prod. Econ., vol. 117, pp. 229-233, 2009.         [ Links ]

[42] C. Basnet and A. Weintraub, "A genetic algorithm for a bicriteria supplier selection problem," Int. Trans. in Operational Research, vol. 16, pp. 173-187, 2009.         [ Links ]

[43] A. Mendoza, and J.A. Ventura, "Estimating freight rates in inventory replenishment and supplier selection decisions," Logistics Research, vol. 1, pp. 185-196, 2009.         [ Links ]