1. Introducción
Las clásicas rutinas de cálculo usadas en equilibrios de fases donde intervienen múltiples componentes suelen presentar problemas de convergencia o altos tiempos computacionales. Una de las más usadas en aplicaciones de equilibrios de tipo ELV, ELL, ESL, ELLV, ESLV (siendo V: vapor, S: sólido y L: líquido) es la Ecuación de Rachford-Rice (ERR); una ecuación resultante del balance de materia de las p fases y c componentes presentes en una mezcla a separar, a condiciones de temperatura (T) y presión (P) constantes 1-3.
La ERR explícitamente es la función base en separadores flash bifásicos y trifásicos, implementados en desalinización industrial de agua para producir agua dulce, en la refinación de petróleo para la reducción de carga de componentes pesados que se alimenta torres de destilación fraccionada 4,5, desparafinado y transporte de crudos o su tratamiento para separar agua, petróleo y arena 2, entre otros. Sin embargo, de manera implícita, esta ecuación al ser un balance de materia de fases (balance total) y componentes, es muy útil para los cálculos de separación en aplicaciones de equilibrio líquido-líquido y líquido-vapor.
La estructura matemática de la Ecuación de Rachford-Rice Generalizada (RR-G) es una función generatriz que permite obtener los balances de masa total (número de fases) y por componentes, como sistemas en estado estable para procesos de separación 1,2,6. Esta naturaleza genera entonces sistemas de ecuaciones algebraicas del tipo Λ×Λ (Λ ecuaciones con Λ incognitas), que se solucionan con métodos iterativos de busqueda lineal (como Wolfe, Goldstein-Price o Armijo)7 o de región factible (superlineal) como los métodos de Newton o cuasi-Newton (Newton-Raphson multivariable, NR-Broyden, NR-Powell-Broyden, NR-Davidon-Fletcher-Powell, Gradiente conjugado, Polak-Ribiere, entre otros)8. Sin embargo, los métodos de convergencia presentan problemas de estabilidad asociado a un efecto fuerte del problema de valor inicial para el arranque de la relación de recurrencia. Es aquí donde la naturaleza del método de Homotopía Diferencial (HD) gana relevancia, debido a que se transforma un sistema de ecuaciones algebraicas no lineales (NL-AE) en un sistema de ecuaciones diferenciales ordinarias no lineales (NL-ODE) que se puede resolver usando métodos multivariables de integración como el caso de Runge-Kutta de 4º orden (RK-4), acoplado al esquema de duplicación para el cálculo del error local de integración9.
Aunque actualmente los paquetes computacionales comerciales reconocidos como Aspen®, COMSOL®, ChemCad® u otros basados en Matlab®, entre otros, poseen estructuras matemáticas y numéricas poderosas (que minimizan los tiempos computacionales, con alta estabilidad y eficiencia en la búsqueda de soluciones), no son de fácil acceso debido a sus altos costos de licencias (incluso académicas). La búsqueda de métodos matemáticos (no necesariamente nuevas propuestas, sino el uso de métodos tradicionales como en esta investigación) que admitan su programación en lenguajes de acceso libre (como Python® o Scilab®, por ejemplo) y que cumplan a cabalidad su función en procesos de separación con múltiples fases y componentes, garantizando alta efectividad en las predicciones, tolerancia numéricas inferiores a τ=10-7 y bajos tiempos de cómputo, se convierte en un objetivo relevante para las matemáticas aplicadas.
En este trabajo se presenta una estructura matemático-numérica para la solución de las ecuaciones de balance multivariables (p fases y c componentes) generadas por la Ecuación de RR-G, usando el método de Homotopía Diferencial y su validación en la predicción de equilibrios trifásicos multicomponentes.
2. Metodología
2.1 Modelado de la Ecuación de Rachford-Rice Generalizada
Cuando una mezcla de N c componentes se divide en N fases, el balance para un componente i está dado por la ecuación de Rachford Rice - generalizada1. La Ec. 1 corresponde al componente i y viene dada por:
En la que 𝑧 𝑖 representa la composición del componente i en la alimentación, X j,i es la fracción molar en la fase j y 𝜓j corresponde a la fracción de fase. Teniendo en cuenta la termodinámica de equilibrio de fases, la Ec. 2 define a K j,i que es el coeficiente de distribución de la fase j para el componente i y tomando una fase de referencia R, se obtienen las relaciones de composición en función de las constantes de equilibrio1.
La Ec. 3 correspondiente al balance de materia global es:
Acoplando y expandiendo las Ec. 3 y 1para la fase R, y reemplazando en la Ec. 2, se obtiene la composición de cada fase (Ec. 4):
Como resultado de las condiciones estequiométricas la suma de las fracciones de cada fase N p debe sumar 1. Restando a la fase de referencia la suma de cada fase se obtiene un grupo de (N p -1) ecuaciones residuales o de discrepancia, las cuales corresponden a la Ec. 5 obtenida por 10 para N p fases y N componentes:
2.2 Restricciones de la Ecuación RR-G
El denominador de la ecuación RR-G, debe cumplir con las restricciones matemáticas de la Ec. 6:
La igualdad a cero de la Ec. 6corresponde a una indeterminación de la ecuación RR-G, en tal caso el espacio de solución factible es confinado en hipercubos para el grupo de valores. En los casos de P = 2 y 3 fases, la igualdad a cero, permite calcular los coeficientes de distribución (K
max
y K
min
) que acotan la solución, por otra parte, para p fases, la nulidad de la ecuación delimita el espacio de solución factible. La desigualdad positiva corresponde a la restricción física de las fracciones de los componentes en cada fase. Por último, la suma de las fracciones de fase debe ser
2.3 Estructuración del Método de Continuación por Homotopía Diferencial
Dado un sistema de ecuaciones algebraicas no lineales (Ec. 7) obtenidas a partir de la función generatriz de RR-G:
Siendo
O 𝜓
k
, (0),∀k:1, 2,…, Np. Introduciendo un parámetro homotópico 𝜆 (Ec. 9) que realiza una perturbación (1- 𝜆) a la función original, al rededor del vector
Donde f [𝜓
j
(𝜆)] representa el vector de funciones con j= 1, …, Np. Así pues, para 𝜆=0, se dice que es una función homotópica de paso nulo f [𝜓
j
(0)]= f [𝜓
j
], y para 𝜆=1 (función homotópica de paso completo), se tiene que f [𝜓
j
(1)]= f [𝜓
j
*
]=0 11, por tanto
Diferenciando la ecuación a ambos lados con respecto a 𝜆, y aplicando la regla de la cadena se obtiene la Ec. 10:
Donde las derivadas parciales 𝜕𝜓 j (m) / 𝜕𝜆 (m) en la iteración m forman el sistema de ecuaciones diferenciales de la Ec. 11.
Para 0≤𝜆≥1
La Ec. 11 es un sistema acoplado de ecuaciones algebraicas lineales, que al solucionarse por el método de eliminación de Gauss-Jordan (con pivoteo parcial y reescalado de columna, para evitar errores de redondeo y de mal condicionamiento) 1,12, conduce a un sistema de ecuaciones diferenciales ordinarias no lineales 𝜕𝜓 i (m+1) / 𝜕𝜆 (m+1) , donde 𝜓 j con j=1,…,N p , es la variable dependiente, 𝜆 es la variable independiente y que satisface el teorema del valor inicial 𝜓 k (0),∀k:1, 2,…, Np, es decir, vector 𝜓j(0) corresponde al vector de arranque que debe solucionar un problema de valor inicial de Cauchy, en el cual las derivadas parciales 𝜕𝜓 j / 𝜕𝜆 se evalúan en el vector de variables x y la función f i se evalúa en el vector de arranque x 0 . Este sistema se integra desde 𝜆=0 hasta 𝜆=1 utilizando el método de RK-4 multivariable con un tamaño de paso apropiado (tal que el error local en cada etapa de integración no exceda a una tolerancia especificada). Para la optimización del tamaño de paso, se utilizó el esquema de duplicación para el cálculo del error local de integración y una tolerancia 𝜏=10−7.
2.3.1 Aplicación del Método de Continuación por Homotopía Diferencial
Los métodos de solución de la Ecuación de Rachford-Rice Generalizada se han validado usando sistemas hipotéticos de p fases y c componentes en cada fase 13-16. Mueses y Machuca 1 usando un método modificado de Newton-Raphson (NR) con amortiguamiento tipo Broyden (NR-B), generaron soluciones hipotéticas aleatorias para fases entre 2≤ 𝑝 ≤8 y hasta con 𝑐=50 componentes hipotéticos en cada fase. En todos los casos evaluados obtuvieron minimización de la norma euclidiana (principio base para el método de Broyden) y por tanto convergencia absoluta para tolerancias numéricas 𝜏=10−7, en máximo 2335 iteraciones. Estos resultados permitieron concluir que el método era invulnerable cuando se aplicaba a sistemas de naturaleza hipotética en sus fases y componentes, con lo cual, un sistema real sería solo un punto más del conjunto de puntos aleatorios de evaluación y estaría contenido en el espacio fase de solución aleatoria de RR-G.
Sin embargo, al probar esta hipótesis se encontró que la aplicación de NR-B a sistemas termodinámicos reales de 𝑝=3 fases y 𝑐=10 componentes, generaba divergencia en la Norma Euclidiana y, por tanto, el sistema no llegó a la convergencia.
Con el fin de probar la robustez del método propuesto y abarcar diferentes configuraciones de distribución de fase, en esta investigación se incluyen diversos ejemplos del cálculos de equilibrio de tres fases con mezclas sintéticas que contienen hidrocarburos de tipo parafinados (sistema de hidrocarburos parafínicos de composición generada en función de los pesos moleculares de los componentes que van desde C1 hasta n-C28,) 17 o mezclas de los mismos con pseudocomponentes y agua (18) , además de una mezcla de etilenglicol, dodecanol y nitrometano 19.
De manera genérica, la estimación de los coeficientes de actividad y fugacidad de los componentes en las fases se realizó así: Modelo de Wilson Predictivo para los coeficientes de actividad en las fases sólida 𝛾 i s , UNIFAC modificado con el modelo de volumen libre de Flory para la fase liquida 𝛾 i L (20 y la ecuación de estado de Soave-Redlich-Kwong-Predictivo (PSRK) para los coeficientes de fugacidad de la fase vapor 21.
2.3.2 Cálculos de Equilibrio de Fases: Acoplamiento de Sustitución Sucesiva y Homotopía Diferencial
Las rutinas numéricas implementadas para la solución de equilibrios de fases basadas en la minimización de la energía de Gibbs 22, implican el uso de dos ciclos iterativos anidados 23, uno externo donde se corrigen las fracciones molares a partir de una fase de referencia 𝑥 𝑖,𝑅 y uno interno para ajuste del balance de materia o cálculo de las fases, por solución de la ecuación de Rachoford-Rice 24,25. El método de Sustitución Sucesiva (MSS) es usualmente estructurado para el cálculo del ciclo externo y el interno con métodos convergentes del tipo Newton 26 los cuales evalúan la convergencia y estabilidad numérica a partir del comportamiento de la norma euclidiana y el número de interacciones. Se establece entonces que la Norma Euclidiana un parámetro idóneo para ser usado en la comparación de la capacidad de convergencia del método (Ec. 12).
Siendo N.E f , la norma euclidiana del vector de funciones de discrepancia fi(𝜓 k ).
De forma general el procedimiento de cálculo se establece así: i) Se introducen las composiciones del alimento y las condiciones de operación, ii) Se asumen los coeficientes de distribución termodinámica iguales a 1, iii) Se soluciona la ecuación de Rachford-Rice para obtener el valor de las fases 𝜓 k (ciclo iterativo interno), iv) se calculan las composiciones de las fases generadas (inicio de ciclo iterativo externo), v) se calculan coeficientes de fugacidad y actividad, vi) Se calculan los coeficientes de distribución termodinámica, vii) Se soluciona la ecuación de Rachford-Rice (ciclo iterativo interno) y se corrigen las fases generadas 𝜓 k , viii) Se estiman las composiciones corregidas de las fases (fin de ciclo externo), ix) Se normaliza las composiciones de las fases, x) se comparan las composiciones corregidas en el paso (ix) con las estimadas en el paso (iv), si su error es inferior a la tolerancia preestablecida (en este trabajo se tomó un ε f =1.0x10−10), entonces paso (xi), sino, vuelve al paso (iv), y xi) resultados 3,27.
Para el cálculo de la distribución de fase en los pasos (iii) y (vii), la estrategia de solución numérica propuesta en este trabajo consiste en generar un sistema homotópico con el parámetro λ (el valor de este parámetro depende el vector de variables de la ecuación de RR-G), para un vector de arranque 𝜓(0), cuyas componentes son los valores iniciales de las fracciones de fase, se tienen que λ=0. Se tiene que λ=1 en el vector solución 𝜓* buscado. Se construye entonces el sistema homotópico con el parámetro λ mediante la relación de la Ec. 9 11,28.
3. Resultados y Discusión
Para demostrar la efectividad de la aplicación de la rutina de cálculo, inicialmente se muestran las simulaciones de la Norma Euclidiana generada en el proceso de convergencia para estimaciones de equilibrio de fases en un sistema de hidrocarburos parafínicos de composición generada en función de los pesos moleculares de los componentes que van desde C1 hasta n-C28. Para esto se compararon el acoplamiento del método MSS-Newton-Raphson-Broyden 29-31 (Figuras 1a y 1b) y el acoplamiento de MSS-HD (Figura 2).
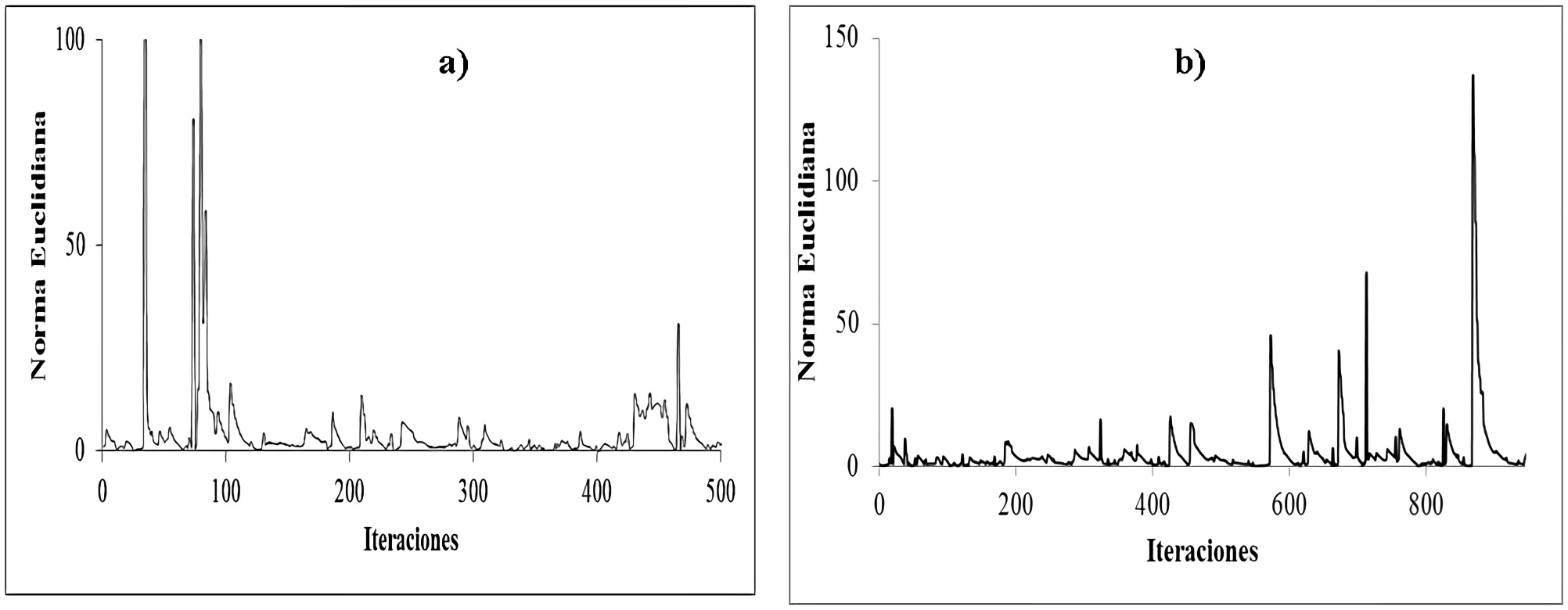
Figura 1 Comportamiento de la Norma Euclidiana MSS en función del número de iteraciones para sistemas hipotéticos con funcionalidad termodinámica de 3 fases. Para la Figura 1a son 20 componentes y 28 en la Figura 1b
Los resultados de la norma euclidiana en función del número de iteraciones obtenidos, corroboran los resultados del comportamiento numérico del método en 29, 30 y 31. El principal inconveniente con este método es como se puede observar su convergencia, aun después de 500 iteraciones el método no converge, sin embargo, presenta intervalos de estabilidad en los cuales la norma euclidiana esta próxima a cero.
La Figura 2, muestra la convergencia de la solución propuesta aplicada en diferentes N c . La primera observación importante es que no existe una relación predecible entre el N c y el número de iteraciones, lo cual es ocasiona las características de inestabilidad y no linealidad de los coeficientes de distribución, al igual que de las funciones de discrepancia 1.

Figura 2 Comportamiento de la Norma Euclidiana de método de Homotopía en función del número de iteraciones para sistemas hipotéticos con funcionalidad termodinámica de 3 fases y 20 ≤ Nc ≤ 28
La naturaleza no lineal de la ecuación RR-G provoca alta vulnerabilidad en los métodos convencionales de solución, el mayor desafío que estos enfrentan en cuanto al cálculo del equilibrio está en generar un buen vector de arranque para las fracciones de fases en un sistema multifásico con Nc componentes, en la actualidad algunos de los enfoques mejor estructurados reportados en la literatura son el propuesto por 31, en cual se usa un parámetro de ajuste basado en la minimización de la función de discrepancia y el de 1, fundamentada en el control del error dentro de los hiperplanos de solución factibles durante el proceso iterativo.
El método de Homotopía tiene un amplio rango de convergencia, pero es necesario partir de una solución inicial adecuada para que converja, un vector de arranque no adecuado podrá resultar en la no convergencia o en convergencia de soluciones no deseadas, mientras MSS no depende de los valores iniciales y permite actualizar las fracciones de fase y las relaciones de equilibrio en el proceso iterativo, sin embargo, converge demasiado lento. Al ser MSS un controlador de las variables de entrada y respuesta del método de Homotopía Diferencial, se pueden combinar los puntos fuertes y evitar los débiles de ambos métodos.
Aunque la efectividad del método es robusta, el método HD pierde su capacidad predictiva en el espacio fase de solución, es decir, es menos preciso que los algoritmos de convergencia iterativa, no obstante, su aplicabilidad radica en su velocidad misma de convergencia y la no vulnerabilidad de las funciones (como en el caso de los sistemas iterativos), por tanto, se recomienda este método si y solo sí, los métodos iterativos son vulnerados.
3.1 Aplicación en sistemas hidrocarburos sintéticos de 20 componentes
En primer lugar se mostrara un cálculo detallado de vapor-líquido-multisolid-(cera) 25, Para este propósito, se utilizó la misma mezcla de hidrocarburo sintético utilizados en la sección 4, en este caso se tiene 20-componentes de C1 hasta n-C20, con una temperatura de 290.15 K y 1.01325 bar, en la cual se considera un enfoque de coeficientes de actividad, para el equilibrio sólido-líquido y coeficientes de fugacidad y actividad en el equilibrio Liquido-vapor, ignorándose cualquier equilibrio sólido-vapor (a temperaturas bajas y presión atmosférica). Se calculan los coeficientes de actividad en las fases sólida 𝛾 i s y liquida 𝛾 i L utilizando el modelo de Wilson predictivo modificado 20 y UNIFAC modificado con el modelo de volumen libre de Flory 21 respectivamente, mientras, que el coeficiente de fugacidad en el equilibrio liquido-vapor se calcula utilizando el modelo de PSRK, los resultados son mostrados en la Figura 3.
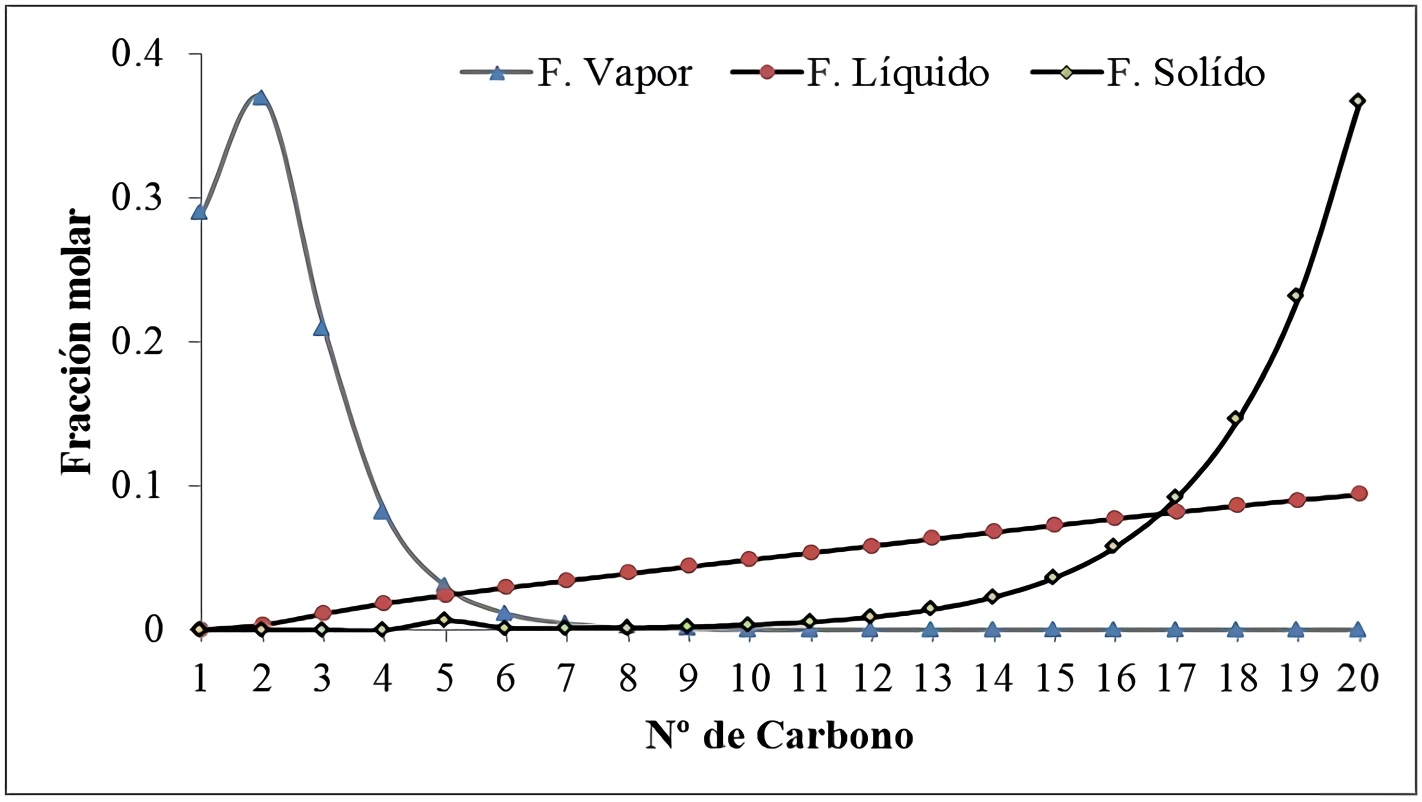
Figura 3 Composición molar de una mezcla de 20 componentes de hidrocarburos parafínicos a una temperatura de 290.15 K y presión de 1.01325 bar, con fracciones de fase de V = 0.04500, L = 0.94743 y S = 0.00757
Con base a los cálculos de equilibrio vapor-líquido-multisolid-(cera) a temperatura y presión fija, mostrados en la Figura 3 se puede ver que el proceso iterativo propuesto para resolver este tipo de equilibrio es simple y computacionalmente eficiente que cualquier método basado en solución de tipo Newton o minimización de la energía libre (25) , debido a que este enfoque converge en menos de 50 iteraciones en mezclas de 20 a 30 componentes y tiene estabilidad en el análisis de predicción para la especie precipitadas en fases sólidas. Además, las estimaciones de las composiciones en cada fase se obtienen directamente sin necesidad de conjeturas de variables involucrada en el proceso de cálculo. Por esta razón, el método propuesto se puede incorporar fácilmente a cualquier sistema de equilibrio vapor-líquido existentes que utilice la ecuación RR-G, extendiendo su aplicabilidad a equilibrios de mezclas experimentales de vapor-líquido-multisolid-(cera) comunes en la industria petrolera.
3.2 Aplicación en mezcla de Alcanos y Agua
En la Figura 4 se pueden observar los perfiles de distribución molar de componentes de una mezcla de alcanos y agua (datos experimentales y calculados) en tres fases (equilibrio tipo EL1L2). Para la evaluación de este equilibrio, se tomaron 100 mol de una mezcla de alcanos (desde C1 hasta n-C20, con igual masa en la mezcla), y se añadieron 40 moles de agua. Los datos experimentales de la mezcla, tales como: fracción de fases, composición en la alimentación y en ca fase fueron reportados por Leibovici y Nichita en 2008 (18) . Se utilizó la ecuación de Soave-Redlich-Kwong (SRK) (27), para generar constantes de equilibrio a 473.15 K de temperatura y 50 bar de presión. Los parámetros de interacción binarios entre los componentes de hidrocarburos son todos cero, sólo entre hidrocarburos y agua no son cero 18.

Figura 4 Composición molar de la mezcla de alcanos y agua a una temperatura de 473.15 K y presión de 50 bar, con fracciones de fase de V = 0.6350, L1 = 0.361 y L2 = 0.0040
El comportamiento de la composición de fases reportadas en 18 para la mezcla de Alcano y Agua a las condiciones de temperatura y presión de 473.15 K y 50 bar, respectivamente, son 0.635801 en la fase vapor, 0.360735 en la fase liquida no acuosa y 0.003464 en la fase liquida acuosa. Los errores de predicción en cada fase son del 0.126 % en la fase vapor, del 0.073% en la fase no acuosa y 15.47% en la acuosa, estos resultados permiten validar el uso del acople del MSS y el método de Homotopía Diferencial en la predicción de fases en equilibrio.
3.3 Aplicación en mezcla ternaria de Etilenglicol, Alcohol de Láurico y Nitrometano
Con el fin de ilustrar la precisión del algoritmo, se usa la mezcla ternaria de Etilenglicol, Dodecanol y Nitrometano, se sabe que tiene tres fases líquidas en equilibrio, pues fue analizada por varios investigadores usando diferentes métodos de cálculo 28. Los parámetros de interacción binarios para los componentes puros se reportan en 19 y la composición de arranque en las fases liquidas se generan de forma aleatoria, los resultados obtenidos con la propuesta de solución presentada en esta investigación se reportan en la Tabla 1.
Tabla 1 Cálculos con el acople de MSS y Homotopía Diferencial para la mezcla Etilenglicol (1), Dedecanol (2) y Nitrometano (3) a Temperatura 295 K con el modelo UNIQUAC 32 y errores en las composiciones y fracciones de fase con respecto a 19.
| x 1 | x 2 | x 3 | ( k | Error de x 1 - x 2 - x 3 (%) | Error de ( k (%) | |
|---|---|---|---|---|---|---|
| Alimento z | 0.4 | 0.2 | 0.4 | |||
| L1 en LLLE | 0.22990 | 0.16247 | 0.62471 | 0.41703 | 60.4 - 28.0 - 14.4 | 4.02 |
| L2 en LLLE | 0.28616 | 0.45924 | 0.25460 | 0.31207 | 1.13 - 1.70 - 4.62 | 1.90 |
| L3 en LLLE | 0.48394 | 0.37829 | 0.13777 | 0.27091 | 49.6 - 53.7 - 46.8 | 4.50 |
| Mezcla de L1, L2 y L3 | f(x 1, x 2, x 3 ) = | 6.6E-10 |
Los resultados en los errores relativos de la predicción de fases mostrados en la Tabla 1, son menores del 5% lo cual se puede considerar admisibles, sin embargo los errores relativos tan altos para las composiciones en cada fase liquida puede deberse a que estas se generan de forma aleatoria, mientras que el trabajo de 19 son cercana en un 80% a los resultados finales, de otra parte la rutina numérica usada para calcular los coeficientes de actividad, no es la misma usada en 19, pues en este se utilizó el modelo UNIQUAC/Ideal/Chemical. Dado que los valores de las fracciones de fases evaluadas en la ecuación de RR-G, son iguales a cero y converge en menos de 15 iteraciones para las tres mezclas estudiadas, por esta razón la propuesta de solución demuestra ser altamente eficiente y estable en la predicción de equilibrio de 3 fases con cualquier número de componentes.
Finalmente, para los tres ejemplos simulados se cumplió la validez de la Ec. 6; en la mayoría de ellos los valores obtenidos para las composiciones en cada fase fueron positivos y menores a la unidad, indicando convergencia sobre la zona factible de separación en equilibrio, resultados comparables con los obtenidos por 1 en sistemas hipotéticos.
4. Conclusión
El método de Homotopía Diferencial es una alternativa numérica eficiente para la solución de la Ecuación de Rachford-Rice en sistemas hipotéticos y reales no lineales, debido a su alta estabilidad, robustez y absoluta de convergencia, incluso con vectores de arranque hipotéticos.
Comparado con Newton-Raphson-Broyden, el método de homotopía ofrece mayor velocidad de convergencia y alta capacidad predictiva de datos experimentales de sistemas reales de equilibrio de fases.















