INTRODUCTION
Motivation
In recent years, conventional distribution systems have dealt with different challenges related to energy efficiency, fast growth in demand, environmental pollution, global warming, dependence on the geographical conditions of the region, among others, which significantly affect the quality and reliability of service to the end user (Giral et al., 2017). These have prompted new forms of generation at the distribution level by integrating renewable energy sources such as natural gas, biogas, wind energy, and photovoltaic plans. This type of generation is also known as distributed generation (DG), and the energy sources involved are called distributed energy resources (DER) (Rafique et al., 2020), which are used to increase reliability and safety in the short, medium, and long term (Carvajal & Marín-Jiménez, 2013).
However, the high penetration and integration of DER have a negative impact on distribution networks. Their impact depends on their location, sizing, and mode of operation (Buitrago-Arroyave & López-Lezama, 2013). This has resulted in increasingly complex systems with several operational problems. The main issues appear with traditional protection schemes, where challenges are noticed such as relay coordination problems due to changes in the grid structure, fault levels, and false tripping, among others (Sarangi et al., 2021; Usama et al., 2021).
To solve these problems, several authors have proposed protection strategies, which adapt conventional relays (overcurrent, distance, differential, undervoltage, among others) to improve their performance in these active distribution networks (ADNs) (Alam, 2019; Barra et al., 2020; Li et al., 2021). The proposed protection schemes focus individually on the relay function, given that each one presents specific problems when applied to ADNs, which is why this review paper presents a comparative analysis of protection schemes implemented specifically using the distance relay.
Consequently, all the analyzed factors are those that can originate malfunction in distance protection, thus affecting the safe operation of an ADN. Thus, studying the countermeasures required to eliminate or reduce these factors’ impact through different protection strategy proposals is essential.
STATE OF THE ART
Distance relays are commonly used in transmission networks. However, they are also considered an essential alternative for ADNs due to their significant advantages compared to other conventional relays (Sinclair et al., 2014). As an example, relay settings depend on the measured impedance, so they are not affected by changes in network topology. Distance relays also have higher sensitivity, selectivity, and accuracy, and their operation is faster than overcurrent relays (Borlase, 2017). However, the main problems with distance protection when operating in ADNs are the infeed effect, fault resistance, directional feature, among others, thus underreaching or overreaching the real impedance and resulting in an erroneous fault detection (Nikolaidis et al., 2018). Another factor to consider is unbalanced faults, which can negatively affect the reliability and speed of distance protection (Sinclair et al., 2014, Jia et al., 2019).
Therefore, several proposals involving adaptive protection schemes based on distance relays have been published in the last years to solve these problems. These approaches aim to reduce the effects of fault resistance or infeed currents (Sinclair et al., 2014). Others implement a compensation factor for zero-sequence (Tsimtsios & Nikolaidis, 2018). In addition, several strategies use different methodologies to define their approach: some are based on voltage drop (Ma et al., 2015) or voltage amplitude comparisons (Liang et al., 2020). Other schemes deal with more specific problems such as determining the fault direction (Chen et al., 2018) or the protection challenges associated with the point of interconnection, as in El-Arroudi and Joós (2018) and Yin et al. (2021). The latter also considers the change produced by the connection of the power transformer at that point, which affects the impedance calculation seen by relay 21.
Another important aspect of distance relays is the adjustment of protection zones. Lavand and Soman (2016) propose predictive analysis to supervise zone 1 of a distance relay using synchrophasors. Ghorbani et al. (2021) provide an accurate non-pilot scheme for an accelerated trip of distance relay zone-2 faults. Regulski et al. (2021) establish the adaptive reach of the 3rd zone of a distance relay with synchronized measurements.
Tsimtsios, Korres, and Nikolaidis (2019) use a communication system to improve the performance characteristics of relay 21, such as improving the speed of digital distance protection. As examples, Jin et al. (2018) employ communication systems based on the IEC 61850 standards; Liu et al. (2019) implement a communication system on an field programmable gate array (FPGA) board, and it is tested using a PSCAD/EMTDC simulator and COMTRADE 99 communication protocols. Despite this, a communication system implies an increase in the operating costs of the network, which is why Tsimtsios, Safigianni, and Nikolaidis (2019a, 2019b) introduce complete guidelines for designing economically feasible distance protection schemes for radial distribution systems with distributed generation (DG).
In addition, some strategies facilitate the estimation of voltage and current signals measured by the relay. Generally, the fast Fourier transform is the most used. Nevertheless, Zamora-Méndez et al. (2016) and Vázquez et al. (2020) implement the second-order Taylor-Kalman-Fourier filter for signal processing analysis, which is faster and with a smaller signal estimation error.
Paper contributions
This paper compares the odds and drawbacks of different protection strategies based on the distance relay applied to ADNs that have been proposed in recent years. It aims to identify and highlight these protection capabilities, which are useful to propose an approach to eliminate the identified gaps in future works.
Distance protection
Fundamental concepts
Protection devices have a fundamental role in electric networks. An essential device is distance protection, also known as relay 21 , which contributes to ensure the continuity and quality of the service for end users (Bansal, 2019). A relay 21 is based on the positive sequence impedance, estimated between the faulted node and the relay location. Therefore, these relays use the measured current and voltage to determine the impedance in the presence of fault conditions (Borlase, 2017).
According to Ma and Wang (2018), the measured impedance at the relay location (Z m ) is presented in Equation (1).
Variables U̇ 𝑚 and 𝐼̇𝑚 are the voltage and the current phasors measured by the distance relay. When the network is in normal operating condition, U̇ 𝑚 is, approximately, the rated voltage, 𝐼̇𝑚 is the load current, and Z𝑚 is the load impedance. However, when a fault occurs, U̇ 𝑚 decreases, 𝐼̇𝑚 increases, and Z𝑚 becomes the impedance between the fault and the relay location. In this way, the distance relay is designed to recognize fault conditions and generate a trip order when Z𝑚 is lower than the zone setting impedance (Z set ), as presented in Equation (2).
The tripping region of the 21 function can be plotted on the R-X plane, as shown in Figure 1, where the protection zone is delimited by Z set , which is the diameter of the circle in the case of mho-type distance protection. Nevertheless, Mohajeri et al. (2015) presents the tripping range as delimited by straight lines, considering other factors such as variations of setting distance, fault resistance, power factor, and measurement errors, thus forming a quadrilateral tripping area, as shown in Figure 2.
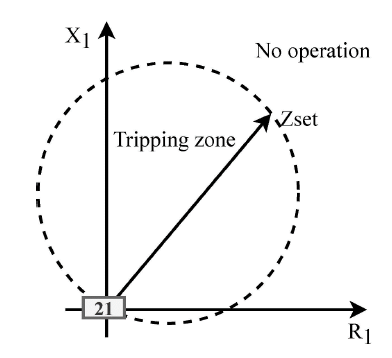
Source: Sinclair et al. (2014), Mohajeri et al. (2015)
Figure 1 Mho-type operational characteristics of distance protection
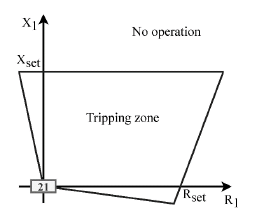
Source: Sinclair et al. (2014), Mohajeri et al. (2015)
Figure 2 Quadrilateral operational characteristics of distance protection
Main issues with distance protection for ADN
Distance relays are generally used in transmission networks. Nevertheless, these have also been considered to be an essential alternative for ADNs, due to their significant advantages in comparison with other conventional relays. As an example, the relay settings depend on the measured impedance, and these are not affected by changes in grid topology (Usama et al., 2021). They also have higher sensitivity, selectivity, and accuracy, and their operation is faster compared to overcurrent relays (Borlase, 2017).
The main issues that cause a malfunction of distance relays when applied in ADNs are presented here. Short lines originate overreach errors in impedance estimation due to the low X/R ratio, since this affects the magnitude of the fault current (Hooshyar & Iravani, 2017). In the case of intermediate sources, the infeed effect is a major influencing factor for distance protection, which affects the measured impedance. This problem results in underreach phenomena because the relay 21 does not measure the total fault current. Similarly, the fault resistance also results in an additional impedance measured by the relay. However, this effect may cause not only underreach but also overreach phenomena. The latter causes the relay not to detect the fault since the impedance seen is outside the protection zone (Nikolaidis et al., 2018).
Other additional problems are related to the directional function, which, in the case of using the positive or negative sequence components, is affected by the harmonic distortion caused by inverter-based DERs (Hooshyar & Iravani, 2017). Moreover, the intensity and nature of the aforementioned effects vary mainly due to the DG penetration level.
DESCRIPTION OF SOME RECENT DISTANCE PROTECTION APPROACHES FOR ADN
Several authors have focused on the advantages and issues of distance protection. Therefore, several strategies have been proposed in the last few years to improve this, especially in the case of ADN application.
A. Approach presented by Sinclair et al. (2014):
The paper by Sinclair et al. (2014) describes the advantages of using distance relays for distribution protection to solve some DG integration problems. To adequately implement distance protection, it is necessary to model the operating characteristics. The paper argues that distance elements derive their operating and polarizing signals from measured voltages and currents. These signals are applied either to the magnitude or angle comparator, from which a trip decision is derived.
As explained above, during normal operating conditions, 𝑍𝑚 equals 𝑍load. In the case of a fault, the measured impedance changes to an impedance with larger inductive and lower resistive components, which is primarily determined by the feeder impedance, from the relay node to the faulted point, as shown in Equation (3) and presented in Figure 3. This last operating condition considers fault 1 (F1).
where, 𝑍 AB and 𝑍 BF1 are the positive-sequence impedance from the substation to the next successive bus, as well as from this node to the fault point.
However, as previously presented, it is necessary to consider the factors that affect the measured impedance. This is shown in Equation (4), where the infeed effect is included.
This effect is due to the presence of DG in node B.
where, 𝑍𝑚,𝑖𝑛𝑓𝑒𝑒𝑑 is the measured impedance considering the infeed effect, 𝐼𝐺1 is the fault current contribution from the utility source and measured by the relay, and 𝐼𝐷𝐺 is the fault current contribution from the DG on node B. If only the fault resistance (R F ) is considered, the impedance seen by the relay 21 is obtained as expressed by Equation (5).
B. Approach proposed in Tsimtsios and Nikolaidis (2018):
The case of the zero-sequence compensation factor (K0) for the correct operation of distance protection during single-line-to-ground faults (SLG) is considered by Tsimtsios and Nikolaidis (2018). In this case, the impedance calculated by the ground distance element is different from the positive-sequence impedance up to the fault position due to the zero-sequence current effect. Thus, to achieve its correct operation, the zero-sequence current is compensated by the 𝐾 0 factor presented in Equation (6), which is included in the relay settings.
where 𝑧0 and 𝑧1 are the per-unit zero-and positive-sequence line impedances from the relay location up to the fault position, respectively, and 𝐾 can be equal to 1 or 3, depending on the relay design. Therefore, the impedance calculated by the relay (𝑧m), considering K0 in case of a phase-a SLG fault is obtained as shown in Equation (7).
where, 𝑍𝑚,𝑛𝑐 represents the non-compensated fault impedance, namely the impedance measured up to the fault point without the consideration of K0.
C. Approach presented by Ma et al. (2015):
Ma et al. (2015) presents an alternative approach that considers the voltage drop under high-resistance faults to propose an adaptive scheme for a quadrilateral-type relay. First, this strategy establishes a voltage drop equation from the relay location to the fault point. Equation (8) shows the voltage drop in a double-source system considering a fault 2 (F 2 ) as in Figure 3.
where Z is the real fault impedance and U̇ m is the voltage at the fault point, which is determined by the multiplication of the fault current (𝐼̇ f ) and resistance (R F ).
For the case of a fault 2 (F 2 ), the voltage and current phasors are shown in Figure 4. Due to the contribution of the opposite side current, 𝐼𝐷𝐺, there is an angular difference, ψ, between 𝐼̇𝑚 and 𝐼̇ f . In addition, 𝜑 line is the impedance angle of the protected line, and 𝜑𝑢𝑖 is the angular difference between U̇ m and 𝐼̇𝑚. Therefore, performing a phasor analysis of Figure 4 from Equation (8), the fault impedance is obtained using 𝑍𝑚, as shown in Equation (9).
The adaptive protection criterion is established from Equation (8). To this effect, it is important to define an adaptive adjustment coefficient (k a ), which is responsible for readjusting the quadrilateral characteristics ( 𝑅 𝑠𝑒𝑡 and X set ) of the distance protection shown in Figure 2. The k a factor is defined in Equation (10).
D. Approach introduced by Liang et al. (2020)
The approach by Liang et al. (2020) proposes a protection scheme based on voltage amplitude comparison. The main objective is to reduce fault resistance problems by using the fault-point voltage, measured current, and setting impedance to establish a virtual measured voltage. The approach is divided into two schemes: the first one identifies in-zone and out-of-zone faults from all types of faults by comparing the amplitudes of the original (U̇ m ) presented in Equation (8) and the virtual (Ů’ m ) measured voltages in Equation (11).
According to Figure 4, a phasor analysis is performed to represent the original and virtual voltages. Consequently, a new distance protection criterion is proposed, as shown in Equation (12).
The second scheme is aimed to identify in-zone and out-of-zone faults under all fault types, based on the improved original and virtual measured voltages. It is considered essential to improve the sensitivity of distance protection because the measured fault voltage varies according to the fault resistance, which can lead to measurement and calculation errors; an in-zone fault may be misidentified as an out-of-zone fault, thus causing a distance protection malfunction.
Consequently, the sensitivity of the proposed protection scheme is then improved by introducing a special voltage phasor (U̇ fset ), which is expressed in Equation (13).
where 𝑈𝑠𝑒𝑡 is the setting voltage. Therefore, the voltages in Equations (8) and (11) are modified by replacing the fault voltage (U̇ 𝑓) with the special voltage phasor (U̇ 𝑓𝑠𝑒𝑡), obtaining the improved original (U̇ 𝑚_𝑖𝑚𝑝) and improved virtual (U̇ ′̇𝑚_𝑖𝑚𝑝) voltages as a result. Thus, the proposed protection criterion shown in Equation (12) is conserved, but the compared magnitudes change with these improved measures. Equations (14) and (15) show the possible values of the U̇ 𝑚_𝑖𝑚𝑝 and U̇ ′̇𝑚_𝑖𝑚𝑝 magnitudes determined from Figure 4.
If | U̇ 𝑓|<𝑈𝑠𝑒𝑡
If | U̇ 𝑓|≥𝑈𝑠𝑒??
where 𝜑𝑓𝑧 is the angular difference between 𝐼̇𝑚𝑍 and U̇ 𝑓, and 𝜑𝑚𝑧 is the angular difference between 𝐼̇𝑚𝑍 and U̇ 𝑚, as presented in Figure 4.
E. Approach proposed by Yin et al. (2021)
A particular case unfolds when DG units are connected at the utility side of the transformer. It is therefore interesting to analyze the problems and challenges associated with the point of interconnection (POI). In Yin et al. (2021), a new distance protection method is presented, whose objective is to introduce an enhanced measured impedance calculation using residual voltage compensation to correctly and timely detect all fault types, particularly SLG faults at the POI. The protection scheme considers a previous analysis of the apparent impedance for SLG faults, aimed to find the root cause of the incorrect apparent impedance seen by the distance relay on the DG side. In this case, the distance relay on the DG integration side sees an SLG fault in the interconnection line as a phase-to-phase fault due to the commonly used delta-wye transformer configuration.
The proposal is based on a residual-voltage-compensated method for reliable POI protection. To this effect, a broken-delta high-voltage transformer (VT) is used to feed the proposed relays 21 on the DG integration side in order to provide residual voltage ( 𝑉 0 ) for calculating the compensated impedance. This adjustment enables the measurement of the correct apparent impedance for all faults, including SLG faults by the relay. The following considerations must be made: (i) 𝑉 0 on the utility side should be converted to the DG side, and (ii) the angle of 𝑉 0 needs to be shifted based on the interconnection transformer winding connection. After considering the impedance compensations for the transformer winding connection used (YD11), the measured impedance for the phase-to-ground ( 𝑍 𝑚,𝑎𝑔 ) can be obtained as shown in Equation (16).
where 𝐼 1𝐷𝐺 is the positive sequence fault current contributions from the DG side. Considering the above, the proposed five-module distance relay is presented in Figure 5. The modules are as follows:
Phasor calculation module: it calculates the phasor values from the CTs and VTs using sampling techniques.
Impedance compensation module: it estimates the compensation factor using the residual voltage at the utility side and the positive-sequence current at the DG side.
Angle shift module: it shifts the angle of V0 based on the interconnection transformer winding configuration.
Impedance calculation module: it calculates the measured impedance based on transformer connection.
Fault detection module: it detects the fault using typical distance relay operation characteristics.
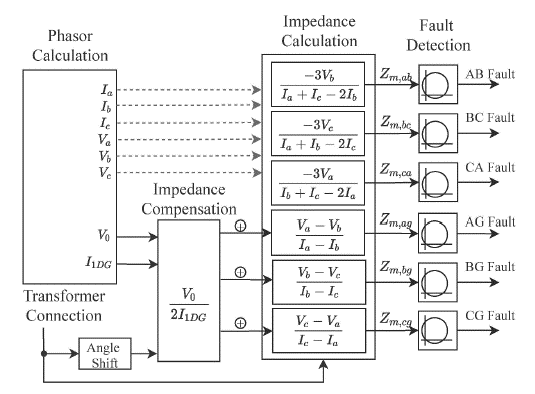
Source: Yin et al. (2021)
Figure 5 Block diagram of distance relay with residual voltage compensation
F. Approach presented by Chen et al. (2018)
The detection of the active power flow direction in case of a fault is critical for the correct operation of 21 protection. Chen et al. (2018) propose a distance relay in the time domain based on the R-L differential equation algorithm, which is suitable for wind power integration systems and also solves the direction identification problem mainly when zero-voltage faults occur.
The proposal considers a directional element based on the time domain and the differentiated characteristics of the memory voltage drop and the actual voltage drop, on equivalent impedance from relay location to power sources under forward and reverse fault conditions. This proposal also includes the correlation criterion to detect the fault direction. In this approach, a model of double-fed induction generator (DFIG) based wind farm with characteristics of the transient electromotive force (EMF) is established. To determine the directional feature, the memory voltages drop (U̇ 1, U̇ 3), and the actual voltages (U̇ 2, U̇ 4) are used as follows:
If Ủ1 and Ủ2 have the same variation trend after the fault, it is a forward fault.
If U̇ 3 and U̇ 4 have the same variation trend after the fault, it is a reverse fault.
These voltages are obtained as shown in Equation (17).
where, U̇ 𝑚,𝑚 and 𝐼̇𝑚,𝑚 are the memory voltage and memory current; and U̇ 𝑚,𝑓 and 𝐼̇𝑚,𝑓 are the measured voltage and measured current after a fault, respectively. Next, if U̇ 𝑚, after the fault is higher than U set , a distance (𝑙) from the relay location to the fault point is calculated based on the R-L differential-equation algorithm, as given by Equation (18). If the estimated distance 𝑙 is larger than the setting value 𝑙𝑠𝑒𝑡, it is an external fault. If 0 <𝑙<𝑙𝑠𝑒𝑡, it is an internal fault. If the estimated distance, 𝑙, is negative, it is an external fault. If the U̇ 𝑚 after the fault is lower than U𝑠𝑒𝑡 the previously described method is used to detect the fault direction.
G. Approach introduced by Tsimtsios, Korres, and Nikolaidis (2019):
Several protection proposals use communication systems to adapt and improve the operational performance of distance protection. As an example, a pilot-based distance protection scheme for meshed distribution systems with DG is proposed by Tsimtsios, Korres, and Nikolaidis (2019). The main contribution of this approach is proposing an efficient protection strategy for meshed grids since most of the networks that integrate DGs are radial, and this scheme provides protection with a considerable fault resistance and under the infeed conditions.
The meshed distribution system used in the test contains forward and reverse distance protection, which is essential to detecting the fault direction in its corresponding zones. The proposed logic depends on these elements, as well as the correct operation of the communication system. The approach proposes that, after the fault impedance estimation, the algorithm checks if it lies inside the forward distance zone. In that case (and after the time required for the relay to respond expires), a permission signal is sent to forward distance elements (FDE). If a permission signal is received from FDE at the same time, the circuit breaker (CB) is tripped. If the CB fails to open, a breaker-failure function is designed for the adjacent CBs.
H. Approach presented by Tsimtsios, Safigianni, and Nikolaidis (2019a, 2019b)
A generalized distance-based protection design for DG integrated MV radial distribution networks is proposed in two parts. The former, presented in Tsimtsios, Safigianni and Nikolaidis (2019a), proposes a complete guideline for designing directly applicable and economically feasible distance protection schemes for medium-voltage (MV) radial distribution systems with distributed generation. In the second part, these guidelines are applied to a real MV radial overhead distribution line with a high DG penetration level. The proposed guidelines intend to take account of distributed generation, dealing with the issues already mentioned in the previous sections and the coordination of relays 21. The procedure is systematic and independent of specific DG conditions, while it must be performed only once for a particular distribution system. Moreover, the designed protection scheme is intended to guarantee simplicity; to this effect, it installs the minimum number of distance relays, given that the proposed guidelines are implementable using existing distance relay technology and without using communication means. This guideline is divided into the following sections: 1) basic protection scheme design, 2) distance zone time setting criteria used to determine the time delay settings and the number of relays 21, 3) distance zones reach setting criteria used to determine the zones reactive/resistive coverage to ensure dependability, 4) unintentional lateral coverage setting criteria to address overreaching of laterals by lower-step distance zones; and 5) the additional setting adjustments.
METHODOLOGY
The approaches analyzed above present several alternatives that contribute to mitigating the problems associated with distance protection applied to ADNs. However, to identify future opportunities to develop research proposals related with that protection, a comparative analysis of the proposals above is considered in this paper, which is presented in Table 1. This qualitative analysis allows identifying research gaps and associated challenges related to applying distance protection relays. As can be seen, no proposal covers all the ADN protection requirements. This represents a challenging task, and it suggests the importance of proposing and developing new strategies for adequate ADN protection.
Table 1 Comparison of protection approaches based on distance relays
| Ref. | Issues | Applied to | Observations | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Infeed Effect | Fault Resist. | Direction | Communic. | 𝐾0 factor | Transmission | Distribution | ADN | ||
| Sinclair et al. (2014) | ● | ● | ● | ● | ● | This considers a perfect performance of the directional relay feature. | |||
| Tsimtsios and Nikolaidis (2018) | ● | ● | ● | ● | The effect of the fault resistance is not considered. The setting criteria for coverage and time delay in case of faults in remote relay areas is not analyzed. | ||||
| Ma et al. (2015) | ● | ● | ● | The proposed scheme is not affected by transition fault resistance or load current in transmission lines, or even in ADN. | |||||
| Liang et al. (2020) | ● | ● | The mitigation of CT saturation and VT errors is considered to improve 21 performance. | ||||||
| Yin et al. (2021) | ● | ● | ● | ● | This proposal provides an economical solution as it can be implemented in the existing distance relay platform. Nonetheless, its application is limited to relays at the POI. | ||||
| Chen et al. (2018) | ● | ● | ● | The direction method is easy to implement within a short data window under zero-voltage faults. This is analyzed only for transmission lines that integrate DG. | |||||
| Tsimtsios, Korres, and Nikolaidis (2019) | ● | ● | ● | ● | ● | ● | ● | This approach depends on a communication system to function properly, which affects the reliability of the protection scheme. | |
| Tsimtsios, Safigianni, and Nikolaidis, (2019a, 2019b) | ● | ● | ● | ● | ● | ● | |||
Source: Authors
Conclusions
This paper provides a comprehensive review of some recent adaptive protection strategies based on the implementation of distance relays in ADNs. The analysis compares the advantages, difficulties, and limitations of these approaches based on their operational characteristics. In addition, the proposals are classified according to the different issues covered in their models, thus affecting the protective device's correct performance. Therefore, it is concluded that, despite all the efforts made to propose solutions to mitigate ADN protection issues, there is no efficient strategy for all types of faults in a selective, sensitive, reliable, and cost-effective way, ensuring minimum supply disruption to consumers. Finally, this paper provides directions for developing more complete strategies to adequately improve the AND protection.



































