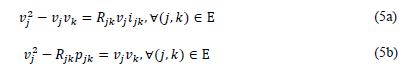INTRODUCTION
For decades, distribution networks have been traditionally designed under the alternating current (AC) paradigm (Starke et al., 2008; Gelani et al., 2019;Garcés et al., 2014). However, in recent years, the accelerated advance in power electronics, renewable generation, and energy storage systems has steered these distribution networks towards the direct current (DC) paradigm (Montoya et al., 2020a; Serra & De-Angelo, 2021). This shift is mainly supported by the following advantages: (i) multiple generation and energy storage technologies work directly with DC technologies (photovoltaic sources, batteries, supercapacitors, and superconducting coils), which implies that the number of power electronic interfaces can be reduced when these are connected to DC networks instead of AC networks (Lotfi & Khodaei, 2017; Hidalgo-Mora et al., 2014); (ii) DC distribution feeders are more efficient in terms of voltage profiles and power losses since reactive power and frequency are non-existing concepts within these grids (Garcés, 2018; Gil-González, et al., 2020; Grisales-Noreña, et al. 2020); and (iii) DC networks are easily controllable since the main goal is to control the voltage profile in all the buses of the grid without the need for frequency synchronization (Parhizi, et al., 2015).
To analyze DC distribution networks, the literature has proposed multiple approaches regarding power flow and optimal power flow analysis. Some of them are nonlinear analysis of DC grids with constant power loads (Simpson-Porco et al., 2015) and convergence analysis of the Newton-Raphson and Gauss-Seidel methods (Garcés, 2017, 2018). The most common approaches in the field are based on second-order, semidefinite programming and interior point methods under nodal representation of the DC network (Bahrami, et al., 2017; Li, et al., 2018; Montoya & Gil-González, 2021) and metaheuristic approaches based on particle swarm and genetic algorithm methods (Grisales-Noreña, et al., 2019). It is worth mentioning that, in the case of optimal power flow analysis, not all methods guarantee optimum global finding, as is the case of nonlinear programming models and metaheuristics (except semidefinite and second-order cone programming). Therefore, alternative methods are required (convex optimization approaches) which find the optimum global by transforming the non-convex solution space of the original model into a convex equivalent model via conic representation. For this reason, in this research, we proposed an alternative branch optimal power flow formulation for DC networks that has previously proposed for AC networks in (Farivar & Low, 2012), with the advantage that, for a DC grid with n nodes and l lines, the number of required variables is 2(n+l), whereas existing convex methods require (n 2 +n) variables (Li et al., 2018). This contribution may significantly reduce the efforts in terms of the processing time.
The remainder of this document is organized as follows: the Branch power flow formulation section presents the exact formulation of the branch optimal power flow model for DC distribution networks; Conic relaxation describes the second-order cone programming model with the relaxed branch optimal power flow; Computational validation presents the test system characteristics and the computational validation of the proposed convex model regarding metaheuristics and exact methods; and, finally, Conclusions presents the main concluding remarks of this research, as well as guidelines for future work.
BRANCH POWER FLOW FORMULATION
The power flow problem and its optimization variants (i.e., optimal power flow models) are classically formulated via nodal representation (Garcés, 2017). In these formulations, it is intended not to use current and branch power variables, which implies that these must be calculated once all the voltage variables are known. However, the power flow problem can be reformulated using branch and nodal variables at the same time by means of the branch-based power flow formulation (Farivar & Low, 2012). Consider the second Tellegen theorem applied to each node of the network except the slack node, which provides the following set of expressions:
where 𝑝𝑗𝑘 (𝑝𝑘𝑚) is the power flow through the line that connects nodes j and k (k and m, respectively), 𝑖𝑗𝑘 is the current flowing through the line that connects nodes j and k, 𝑝𝑘 is the power injection at node k defined as demand minus generation, and 𝑅𝑗𝑘 represents the resistive effect in line j-k. Note that Ε is the set that contains all the branches of the network. Ohm's law applied at each branch results in
with 𝑣𝑗 and 𝑣𝑘 being the voltage values at nodes j and k, respectively.
The power in the DC networks for each branch is defined as
To formulate the optimal power flow model, the scientific literature widely uses the minimization of power losses in all branches, which generates the following nonlinear programming optimization model:
Objective function:
Set of constraints:
Remark 1. The optimization model defined in (4) is known in the literate as the optimal branch power flow model (Farivar & Low, 2012), which is nonlinear and non-convex due to the square of the currents in (4b) and the product between voltages and currents in (4d).
Note that an equivalent optimization model can be obtained from (4) by making some algebraic manipulations. To this effect, let us pre-multiply (4c) by 𝑣 j , which produces
Now, if we raise (4c) to the square in both sides, we have:
Note that, if Equation (6b) is substituted into Equation (5b) and some algebraic manipulations are made, it yields
To obtain an equivalent model, let us define two auxiliary variables, 𝑙𝑗𝑘=𝑖𝑗𝑘 2 and 𝑢𝑗=𝑣𝑗 2.. With these new variables, the optimal branch power flow model (4) can be rewritten as follows:
Objective function:
Set of constraints:
Remark 2. The optimal branch power flow model defined in (8) is still non-convex due to the presence of the product between auxiliary variables 𝑢𝑗 and 𝑙𝑗𝑘 in equality constraint (8d). However, this complication can be dealt with by using a conic relaxation through its hyperbolic representation, as presented in the next section.
CONIC RELAXATION
Conic optimization is a subfield of convex optimization that allows relaxing some class of optimization problems using second-order cone constraints (Farivar & Low, 2012), which is especially attractive when faced with products among continuous variables. Even if the cones are nonlinear inequality constraints, they are convex since these constraints are in the interior space of the cone (Benson & Sauglam, 2013). Then, the conic relaxation of the branch optimal power flow model consists of rewriting (8) with its hyperbolic equivalent (Farivar & Low, 2012). To do so, let us consider the following relation:
Now, if we substitute (9) into (8d), then, we have
Observe that (10) can be rewritten using the Euclidean norm as follows:
Remark 3. The structure of Equation (11) is still non-convex due to the equality sign. However, as suggested byFarivar and Low (2012), this can be relaxed with a lower-equal symbol, which allows (11) to become a second order conic constraint.
With the conic relaxation of (12), the branch optimal power flow model defined in (8) takes the convex structure of (13).
Objective function:
Set of constraints:
Remark 4. The most important characteristic of the second-order cone programming branch optimal power flow model defined in (13) is that it guarantees finding the global optimum with interior point methods under well-defined voltage and demand conditions (Li et al., 2018). In addition, this convex relaxation creates a lower number of variables than the classical convex models reported in the literature, such as semidefinite programming (Bahrami et al., 2017) and SOCP models that only work with voltage variables (Li et al., 2018).
It is worth mentioning that this research does not present the methodology for a solution, since the main contribution of this research is indeed the convexification of the exact nonlinear programming model (8) using second-order cone programming as presented in (13). This implies that, due to the convexity of the solution space and of the objective function with any convex optimizer (e.g., CVX for MATLAB or CVXPY for Python), it is possible to reach the global optimum of the studied problem with a 100% of repeatability properties.
COMPUTATIONAL VALIDATION
To demonstrate the effectiveness and robustness of the proposed SOCP model presented in (13), we considered a large-scale medium-voltage distribution network composed of 69 nodes and 68 lines (radial configuration) with the configuration depicted in Figure 1.

Source: Montoya et al. (2019a)
Figure 1 Schematic connection among nodes for the 69-node test feeder
The 69-node test feeder operates at 12.660 V. All the numerical information of this test feeder can be consulted in the work by Montoya et al. (2019a). For this test feeder, we considered the likely dispatch of three distributed generators located at nodes 21, 61, and 64, with maximum generation capabilities of 12 pu each (Montoya & Gil-González, 2021). In addition, to compare the performance of the proposed SOCP optimization model, we considered different metaheuristic approaches, typically reported in the literature for optimal power flow analysis in DC networks, namely black-hole optimization (BHO) (Velasquez et al., 2019), elephant swarm water search algorithms (ESWSA) (Montoya et al., 2019b), continuous genetic algorithms (GGA) (Montoya & Gil-González, 2021), sine-cosine algorithms (Giraldo, et al., 2019), vortex search algorithms (Montoya, et al., 2020b), and an exact approach based on interior points available in the GAMS software (Montoya & Gil-González, 2021).
Table 1 shows the numerical performance of all the comparative methodologies for optimal power flow analysis in DC grids. It is worth mentioning that all the metaheuristic methods were evaluated 100 times to determine the best possible solution reached by each one of them.
Table 1 Numerical results in the OPF problem with different comparative approaches
| Method | Generation (kW) | Power losses (kW) |
|---|---|---|
| BHO | [460,21, 1170,28, 639,88] | 5,025771 |
| ESWSA | [495,80, 1049,55, 699,62] | 5,005033 |
| CGA | [401,31, 1191,55, 584,05] | 4,982861 |
| SCA | [499,86, 1199,90, 564,26] | 4,557555 |
| VSA | [455,47, 1200,00, 584,85] | 4,454562 |
| GAMS | [453,21, 1200,00, 585,16] | 4,454342 |
| SOCP | [453,22, 1200,00, 585,17] | 4,454342 |
Source: Authors
The numerical results in Table 1 reveal that:
The best metaheuristic approach for dealing with optimal power problems in DC distribution networks is to the VSA approach. Its variations regarding the optimal solution are in the order of milliwatts, which constitutes an exact methodology from the numerical point of view.
The worst behavior regarding metaheuristics for optimal power flow solution is the result reported by the BHO. This is due to the fact that it is a simplification of the classical particle swarm optimizer, which is easily stuck in local optimal solutions (Gupta et al., 2016).
The proposed SOCP model for optimal power flow analysis in DC distribution networks allows reaching the global optimum solution for this problem since its solution matches with the interior point method available in GAMS. This is to be expected, as the solution of the SOCP models has been elaborated with interior point methods in the scientific literature (Benson & Sauglam, 2013).
Figure 2 presents the percentage of power losses minimization, considering that the base case without distributed generation has an initial power loss of about 153,847557 kW.

Source: Authors
Figure 2 Improvement of the power losses reached by the proposed SOCP reformulation and the comparative methods
Note that the results in Figure 1 confirm that VSA, GAMS, and the proposed SOCP approach are the best methodologies regarding power losses minimization via optimal power flow analysis with distributed generation. Also, the most important implication of these results is that, in the case of DC networks, the total power losses can be minimized by up to 90%, which is not the case, with most of the results reported for the 69-nodes test feeder with distributed generation around 60% (Kaur, 2014). This difference between both technologies can be attributed the reactive effects inherent to AC networks, which do not arise in the case of DC distribution.
CONCLUSION
A second-order cone programming model for optimal power flow analysis in DC distribution networks that combines nodal and branch variables has been presented in this paper. The exact nonlinear programming model was convexified via the relaxation of the power sent from nodej to node k, i.e., 𝑝𝑗𝑘 = 𝑣𝑗 𝑖 𝑗𝑘, with its conic equivalent of hyperbolic representation. The numerical results in the 69-node test feeder demonstrate that the proposed SOCP model allows reaching the global optimal solution for the optimal power flow problem in DC distribution networks with distributed generators, given that its results are better than metaheuristic methods such as BHO, ESWSA, CGA, and SCA. In addition, numerically speaking, the only metaheuristic method that can reach a near-optimal solution is the VSA approach, which was compared with the proposed SOPC model and the interior point methods available in the GAMS software.