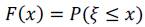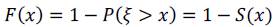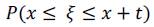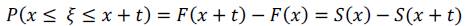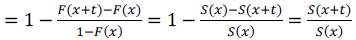Introducción
El sector de manufactura ha venido enfrentando problemas relacionados con la globalización, el desarrollo tecnológico, la innovación de productos y nuevos procesos; además, tiene que involucrarse con factores de sostenibilidad ambiental, disminución de la pobreza e inequidad y crecimiento económico (León, Vásquez y Vergara, 2018). Bajo este contexto, analizar la demografía empresarial de este sector implica la revisión de los índices de natalidad, el tiempo de vida y la mortandad; puntos relevantes para comprender la evolución del sector entre 1901 y 2018, periodo caracterizado por crisis financieras, estancamientos económicos, guerras, caída del precio del petróleo, depresión económica, caída de las bolsas de valores, desaceleración de la economía mundial, entre otros.
Cuando se hace referencia a lo que es el cierre de las empresas, por lo general, se identifica como si este fuera un fracaso; sin embargo, es necesario diferenciar los dos conceptos. El cierre empresarial puede ser entendido como la incapacidad de la empresa para continuar en el mercado, es decir, una interrupción en el negocio que se convierte en un problema grave, si se tiene presente que las empresas son el motor económico de los países. Puebla, Tamayo y Feijoó (2015) aseveran que los factores asociados a la supervivencia empresarial están clasificados en tres grupos:
Características del entorno: crecimiento del sector, creación neta, concentración, tamaño de la industria y localización geográfica.
Factores propios de la empresa: tamaño inicial, capital individual o colectivo, salarios, rentabilidad, productividad y publicidad.
Características del empresario: aversión al riesgo, capacidad de innovación, expectativa de éxito y experiencia.
Por otro lado, el fracaso empresarial está vinculado a la falta de recursos financieros, el mismo que lleva al empresario a cesar las operaciones comerciales (González, Arteaga y Ruíz, 2018). Mures y García (2004) distinguen tres estados distintos de fracaso:
Fracaso económico: cuando los ingresos son insuficientes para cubrir los costes.
Fracaso financiero, denominado de insolvencia: consiste en problemas de falta de liquidez.
Fracaso jurídico o insolvencia definitiva o en el sentido de bancarrota: se identifica con la existencia de un patrimonio neto negativo de la empresa, lo que conlleva una sanción legal.
Debido a la importancia y el impacto que provoca el cierre de empresas, en los últimos años un término nuevo se discute en este ámbito: la noción de resiliencia, término que describe cómo una entidad o sistema responde a golpes y perturbaciones, como es el caso de crisis financieras o recesiones económicas. De acuerdo con Martin y Sunley (2015), la resiliencia económica regional se define como la capacidad que tiene una región para recuperarse con éxito de los choques en su economía, que la desvían de su trayectoria de crecimiento. En el ámbito empresarial, se utiliza esta idea en discusiones sobre las estrategias que las empresas deben adoptar para sobrevivir y prosperar en un mercado global cada vez más cambiante. Bajo este contexto, Williams y Vorley (2014) recalcan la importancia del emprendimiento como motor de crecimiento económico, el cual debe ser considerado como un factor crucial que influye en la resiliencia y en el que las empresas pequeñas gozan de ventajas al momento de responder a choques externos, como mayor flexibilidad, adaptabilidad y son capaces de innovar para adaptarse a las nuevas circunstancias. Por otra parte, Bamiatzi y Kirchmaier (2014) aseveran que las empresas más grandes poseen ventajas como las economías de escala, el acceso al capital, las opciones de inversión más amplias, mayor poder de negociación, etc., lo cual sugiere una relación positiva entre el tamaño de la empresa y su desempeño general en entornos en declive. Por esta razón, no se pueden generalizar los resultados de una investigación, pues las pequeñas empresas no son simplemente versiones reducidas de grandes firmas, por lo que debería existir un análisis independiente.
Se puede deducir que un entorno adverso no inhibe necesariamente el crecimiento de la empresa, ya que pueden invocarse estrategias específicas para superar las condiciones volátiles del mercado; en este escenario, la capacidad de respuesta juega un rol fundamental. Además, las últimas investigaciones referentes al término resiliencia conllevan el análisis en el campo de las finanzas como un sistema, para, de esta manera, proporcionar respuestas a las causas de su rompimiento y generar escudos o protecciones para las economías en general.
Lo descrito es importante en el ámbito latinoamericano, pues estas economías presentan inestabilidad y son susceptibles a los efectos de las crisis. En el caso ecuatoriano, se han realizado algunos estudios sobre el tema de cierre empresarial, entre los que se destacan los trabajos de Bermudez y Bravo (2019), quienes analizaron la probabilidad de cierre empresarial de las mipymes en el periodo 2007-2016, y el de Puebla, Tamayo y Feijoó (2018), en el que se analizaron los factores asociados a la supervivencia y muerte empresarial en el periodo 2009-2015.
El presente estudio se enfoca en analizar la demografía empresarial del sector manufacturero ecuatoriano con base en los datos de la Superintendencia de Compañías, Valores y Seguros ([Supercias], 2019) en un periodo de 118 años; además, propone un modelo actuarial de cierre empresarial para determinar la mortalidad de las empresas del sector.
Se ha determinado en el estudio que la esperanza de vida de una empresa recién creada es de 14,27 años, además, que las empresas que llegan a los 70 años de creación tienen una esperanza de vida de 21,13 años más. Se destaca que desde este punto en adelante existe una tendencia decreciente en el periodo de funcionamiento empresarial.
2. Revisión de literatura
Existe un sinnúmero de estudios y modelos desarrollados a lo largo del tiempo concernientes al cierre, fracaso o quiebra empresarial. La mayoría de estos se enfocan en un concepto de riesgo de insolvencia, que está relacionado con la quiebra empresarial; tema que ha sido analizado por diversos autores. Entre ellos se destaca FitzPatrick (1932)) que fue uno de los primeros en investigar el fracaso empresarial analizando la variación de las ratios financieras uno año y dos años antes de la quiebra de las empresas. Beaver (1966) propuso la “predicción” del fracaso empresarial y sugirió una metodología para la evaluación de datos contables con miras a diferentes propósitos, y no solo para determinar la solvencia. Altman (1968) evaluó la calidad del análisis de razones financieras como técnica analítica: la predicción de la quiebra empresarial se utiliza como caso ilustrativo. El autor eligió el análisis discriminante múltiple (ADM) para su investigación y aseveró que las empresas en quiebra presentan ratios significativamente diferentes a las empresas que continúan operando. De esa época también destaca el trabajo de Ohlson (1980)) quien introdujo por primera vez en este campo el uso de modelos logísticos condicionales.
Luego, se empezaron a introducir modelos no paramétricos para predecir de manera más eficaz el cierre empresarial. Algunos de los modelos no paramétricos conocidos son las redes neuronales artificiales, los modelos hazard (modelos de peligro), los modelos difusos, los algoritmos genéticos y los modelos híbridos, o modelos en los que se combinan varios de los modelos anteriores. Dentro de estos estudios se puede mencionar el de Odom y Sharda (1990), quienes realizaron una investigación para el análisis de predicción de bancarrota con un análisis discriminante multivalente y una red neuronal. Zhang, Hu, Patuwo y Indro (1999) explicaron el papel de las redes neuronales artificiales para la predicción de la bancarrota en las empresas. Ahn, Cho y Kim (2000) propusieron un sistema híbrido inteligente que predice el fracaso de las empresas en función de los datos de rendimiento financiero, combinando el método rough set y las redes neuronales. Hua, Wang, Xu, Zhang y Liang (2007) se enfocaron en el problema de precisión de los vectores de soporte automático (SVM) aplicados a la predicción de quiebra, con el propósito de diseñar una aplicación que genere mayor precisión. Berg (2007) utilizó modelos aditivos generalizados (GAM) como alternativa flexible no paramétrica para la predicción de la quiebra y para mostrar que es significativamente mejor que el análisis discriminante, que los modelos lineales y que las redes neuronales. Ghazali, Jaafar Hussain, Mohd Nawi y Mohamad (2009) utilizaron redes neuronales de orden superior (HONN) para predecir las tendencias futuras de las señales financieras: la red neuronal Pi-Sigma y la red neuronal polinomial de cresta. Bajo la misma perspectiva de análisis, McKee y Lensberg (2002) investigaron un enfoque híbrido para la predicción de quiebras, en el que indican que la programación genética junto con la teoría de conjuntos aproximados pueden ser un enfoque de modelado híbrido eficiente y efectivo para desarrollar un modelo robusto de predicción de quiebras. El proceso condujo a la identificación de 11 factores predictivos que son altamente significativos: 1) tamaño de la empresa, 2) rentabilidad, 3) gestión del capital circulante, 4) largo plazo de inversión, 5) gestión financiera, 6) calidad de ganancias, 7) opinión de auditoría previa, 8) rotación de capital, 9) posición de efectivo, 10) capitalización ganada y 11) apalancamiento.
Monelos, Sánchez y López (2016) realizaron un análisis comparativo de la eficacia de ocho métodos de predicción de quiebra: 1) univariante, 2) regresión lineal, 3) análisis discriminante y logit, 4) particionamiento recursivo (árboles de decisión), 5) rough sets, 6) redes neuronales artificiales y 7) data envelopment analysis (DEA). De acuerdo con los autores, los modelos deben ser interpretados en conjunto, en términos de parsimonia o simplicidad; el modelo más parsimonioso para un horizonte de pronóstico de tres años resultaría ser el logit; en el extremo opuesto, las redes neuronales artificiales requieren un número mayor de variables y poseen mayor complejidad operativa.
En el ámbito ecuatoriano, Bermudez y Bravo (2019), a través de los modelos probit, logit y complementary log-log regression (cloglog), analizaron factores que inciden en la probabilidad de cierre empresarial de las mipymes y con los que se estima que la esperanza de vida de las empresas es mayor al incrementarse el apalancamiento financiero, disminuir las cuentas por cobrar, invertir en activo fijo neto y mantener niveles altos de rentabilidad. De acuerdo con los resultados, el tamaño presenta una relación no significativa con la supervivencia empresarial, además, pertenecer a la región Sierra y contar con más años de antigüedad disminuye las probabilidades de cierre. De igual manera, en esta investigación se asevera que que la ausencia de endeudamiento no necesariamente indica una menor probabilidad de fracasar, por el contrario, resulta beneficioso para que las mipymes se apalanquen y de esta forma aumenten su esperanza de vida. De igual forma, Puebla et al. (2018) analizaron los factores asociados a la supervivencia y muerte empresarial para el caso ecuatoriano, mediante el uso de la técnica no paramétrica Kaplan-Meier y el modelo de Cox (semiparamétrica). Entre los hallazgos principales de los autores se encuentra que las empresas con mejores perspectivas de supervivencia poseen niveles equilibrados en atributos como la edad, el género y la participación de empleados con educación superior. Además, la tasa de riesgo de desaparecer muestra una relación negativa con el tamaño inicial de las empresas y con el nivel de remuneraciones que pagan.
Existen múltiples estudios que tienen como objetivo lidiar con problemas de clasificación empresarial y mejorar los resultados de predicción de quiebra; en este contexto, el desarrollo de métodos estadísticos y de técnicas de aprendizaje automático han sido de gran aporte. Acosta y Fernández (2007) investigaron la predicción del fracaso empresarial, para esto seleccionaron las ratios financieras con base en una aproximación heurística denominada algoritmo genético, que permite explorar un universo de diferentes modelos, y obtuvieron como resultado las variables independientes más utilizadas, como el índice de liquidez, la liquidez inmediata, los días de tesorería y el endeudamiento con los gastos financieros. Balcaen y Ooghe (2006) realizaron una descripción general de la problemática de las metodologías estadísticas clásicas, sobre todo la relacionada con los modelos discriminantes multivariantes y los modelos logit. Los autores determinaron que los problemas principales son las definiciones arbitrarias, la no estacionariedad y los datos inestables, la selectividad de muestreo y la elección de los criterios de optimización; así como la negligencia de la dimensión temporal del fracaso y el enfoque de la aplicación en los modelos de predicción de fracaso empresarial. Correa, Acosta y González (2003), en su estudio con una muestra de pymes de Santa Cruz de Tenerife, España, utilizaron como criterio para calificar una empresa insolvente el concepto de quiebra técnica, es decir, aquellas empresas que presentan pasivos mayores a los activos. La metodología utilizada fue una combinación del análisis estadístico, factorial y logit, e inteligencia artificial a través del algoritmo; se seleccionaron estos métodos por la flexibilidad y porque no están sujetos a restricciones de normalidad. Mensah (1984) realizó un estudio entre enero de 1972 y junio de 1980 en el que aseveró que la precisión y la estructura de modelos predictivos difieren entre entornos económicos; mencionó, además, que se puede esperar que los diferentes entornos económicos tengan un impacto en la estacionalidad de los modelos de producción de quiebra. Bajo este contexto, los modelos multivariados no captan este comportamiento no estacionario. Se emplea el modelo logit, y las variables más importantes a la hora de explicar la quiebra empresarial son la capacidad de generar flujos de efectivo, liquidez, apalancamiento financiero y rotación de acciones.
Schumpeter (1942) habló sobre la destrucción creativa, demostró que el capital se mueve a través del tiempo de sectores menos rentables a sectores con mejores perspectivas. El cierre de una empresa puede ser una tragedia para las personas vinculadas directamente con ella. Para Schumpeter (1942), las quiebras son una parte esencial del capitalismo y tienen un lado positivo, de hecho, los factores de producción al ser utilizados por compañías ineficientes no brindan los máximos beneficios posibles, de esta manera, si una empresa cierra o quiebra, los recursos se liberan a otras empresas y actividades que generan mayores ganancias.
Stinchcombe (1965) realizó un estudio sobre la mortalidad de las empresas en el que expuso que las tasas de mortalidad son mayores en establecimientos más jóvenes; dicha afirmación la respaldó con observaciones en plantas de producción de Estados Unidos, Argentina e Irlanda y la base teórica que propuso se da por los requisitos adaptativos. La entrada al mercado toma tiempo para que las empresas jóvenes ganen competencias y construyan relaciones que garanticen su capacidad de supervivencia (Hannan, 1998); por tanto, las nuevas empresas tal vez sean más susceptibles a perturbaciones de mercado.
La hipótesis planteada por Stinchcombe (1965) es discutida por Bruderl y Schussler (1990) en un estudio realizado a empresas comerciales de Alemania Occidental. Descubrieron que la hipótesis planteada por Stinchcombe (1965) no es una buena aproximación al riesgo de mortalidad en las empresas de la localidad alemana. Las empresas están protegidas contra el riesgo de cierre en el periodo inmediato posterior a su establecimiento, ya que disponen de un amortiguador de capital inicial.
Otra perspectiva es que su tasa de mortalidad crece conforme aumenta la edad; esta idea se fundamenta en el análisis del comportamiento demográfico de las personas y la idea que engloba este análisis es que las empresas de edad acumulan reglas, son menos flexibles, estancan las relaciones con los consumidores, los mercados de insumos las hacen menos ágiles y su reconfiguración es más costosa a medida que avanza el tiempo (Henderson y Clark, 1990).
Por otro lado, Daepp, Hamilton, West y Bettencourt (2015), en su estudio titulado “La mortalidad de las compañías”, analizaron 25 000 empresas norteamericanas que cotizaron en bolsa entre 1950 y 2009; concluyeron que la tasa de riesgo es aproximadamente constante durante largos periodos de observación y que la tasa de mortalidad es independiente a la edad de la empresa; además, encontraron que la vida típica de una empresa que cotiza en la bolsa de valores es aproximadamente de diez años, independiente del sector industrial en el cual trabajen.
Alva (2017), en su estudio sobre la desaparición de las microempresas en Perú, mencionó que el 95 % de las empresas en este país son micro y generan empleo a casi la mitad de la población ocupada. El objetivo del estudio fue profundizar en las razones por las que las microempresas cierran. Entre los factores de mortalidad están la falta de publicidad, la situación económica del país, la alta cantidad de competencia situada cerca del negocio, la falta de plan de negocio, los mecanismos de control efectivo y la dificultad para conseguir nuevos trabajadores.
En la literatura consultada, hasta este punto, se encuentran análisis correlacionales mediante la aplicación de modelos econométricos o redes neuronales con el objetivo de predecir la quiebra, mientras que en el presente estudio se aplica un análisis desde una perspectiva actuarial a los fenómenos observados, concernientes al cierre empresarial, a través de la elaboración de una tabla de mortalidad empresarial. Ortega (1987) define la tabla de mortalidad o tabla de vida como un instrumento o esquema teórico que permite medir las probabilidades de vida y muerte de una población en función de la edad; además indica que este esquema provee la más completa estadística de mortalidad. Existen pocos estudios sobre el cierre empresarial desde un enfoque actuarial. Fuentelsaz, Gómez y Polo (2004) realizaron un estudio con el fin de mostrar la aplicabilidad del análisis de supervivencia empresarial desde un punto de vista no paramétrico aplicando el análisis con el método de Kaplan-Meier. Pereira, Crespo y Sáez (2019) propusieron un modelo de supervivencia con base en una regresión de Cox, cuya variable dependiente es el tiempo de supervivencia o la tasa de riesgo; asumen que las empresas fracasadas y no fracasadas son de la misma muestra poblacional y consideran a las empresas no fracasadas como observaciones censuradas. Las variables independientes fueron indicadores financieros.
En Colombia, Ng-Henao (2015) analizó la supervivencia de las empresas del sector industrial de Medellín creadas entre los años 2000 y 2010; calculó la probabilidad de supervivencia con base en los tamaños de las empresas al momento de nacer, según la forma jurídica y por ramas de la industria y encontró que las microempresas son las que tienen más dificultad de sobrevivir en relación con las pequeñas, medianas y grandes. Para este análisis utilizó las tasas de entrada y salidas brutas y netas, la tasa de rotación y las funciones de supervivencia y riesgo.
2.1 Estatus de las empresas analizadas
El estatus de las empresas, de acuerdo con la Ley de Compañías, y su reglamento, de acuerdo con Supercias, indica los siguientes estados legales:
Inactiva. Supercias declara inactiva a una compañía que no ha presentado los documentos previstos en el artículo 20 de la Ley de Compañías durante dos años consecutivos.
Disolución y liquidación (por persistir inactividad). Si persiste la inactividad, luego de transcurrir el tiempo estipulado en el artículo 3, el superintendente o su delegado podrá declarar el oficio de disolución y ordenar la liquidación de la compañía.
Cancelación. Concluido el proceso de liquidación, a pedido del liquidador, el superintendente de Compañías, Valores y Seguros dictará una resolución en la que se ordene la cancelación de la inscripción de la compañía en el Registro Mercantil.
3. Metodología
En la primera parte de esta investigación, para comprender la dinámica empresarial, se describe a través del análisis estadístico el comportamiento de los índices de natalidad, crecimiento y mortalidad de las empresas; se clasifican por tamaño, localización y tipo de organización.
Para analizar la vida empresarial de las empresas manufactureras en Ecuador, se puede recurrir a tres métodos: paramétricos, semiparamétricos y los no paramétricos. Los métodos paramétricos asumen una determinada distribución, por ejemplo, una distribución normal, y, con esto, se asume homocedasticidad en la varianza y observaciones independientes. También, existen otras distribuciones utilizadas como son las exponenciales, Weibull lognormal, logit, etc. Los métodos no paramétricos no suponen de manera explícita la forma funcional de la distribución de probabilidad en las observaciones de la muestra. En este tipo de métodos, no es necesario hacer el supuesto de homocedasticidad y además las observaciones no son independientes; estos métodos son el método de Kaplan-Meier, el estimador de Nelson-Aalen, el método de las tablas de mortalidad, etc. Mientras que los métodos semiparamétricos usan una combinación de los dos métodos anteriores (Fuentelsaz et al., 2004).
En este artículo, para el cálculo de probabilidades de supervivencia, cierre, fuerza de mortalidad y esperanza de vida de las empresas manufactureras ecuatorianas, se realizó una tabla de mortalidad. De acuerdo con Promislow (2011), normalmente en el trabajo actuarial de seguros de vida el objetivo es estimar un modelo de fallecimiento/quiebra, el cual muestra un grupo de personas/empresas; la forma básica para observar esto es a través de una tabla de mortalidad. Promislow (2015) indicó que la tabla de mortalidad es un instrumento utilizado en la matemática actuarial, cuya aplicación se da en el campo demográfico y en la biometría actuarial. A través de esta tabla se puede observar la dinámica y evolución de la mortalidad de un grupo de personas, llamado el colectivo inicial, cuyo uso es de suma importancia para la toma de decisiones tanto públicas como privadas. La tabla de mortalidad es una tabulación del número de individuos o entes sobrevivientes (l x ) y el número de individuos fallecidos o entes cerrados (d x ), donde x es un número entero no negativo, l 0 es el número de empresas recién creadas y será un número arbitrario que generalmente es de 100 000.
Por tanto, se definirá la tabla de mortalidad como un modelo teórico que describe el tiempo de vida de una cohorte ficticia que muestre los mismos patrones de mortalidad que una población determinada en un momento dado. En dicha tabla, se pueden expresar las probabilidades de fallecimiento/cierre/ quiebra o supervivencia de los miembros de una población.
El modelo de una tabla de mortalidad normalmente se aplica a poblaciones demográficas, pero se puede adaptar a cualquier colectivo que será analizado en su evolución vital, que en este caso se aplica a la población de empresas manufactureras de Ecuador, con información desde el año 1901. Por este motivo, el presente trabajo realiza un análisis de “demografía empresarial”, de tal manera que, en lugar de trabajar con conceptos de supervivencia y fallecimiento de personas, se trabaja con los conceptos de supervivencia y cierre empresarial.
La importancia del estudio de la dinámica empresarial y los procesos de creación empresarial radica en la correlación que existe entre el número de empresas y la actividad económica, por lo que, a mayor número de empresas, mayor será el PIB per cápita de los habitantes de una determinada región.
Para empezar, es necesario conocer algunos conceptos relacionados con la matemática actuarial con base en Bowers, Gerber, James, Jones y Nesbitt (1997) y Agudelo, Franco y Franco (2016), que se utilizaron para la construcción de la tabla de cierre empresarial: sea x la edad actual de una empresa, por lo tanto x estará ubicada en algún punto entre 0 y el límite superior de supervivencia (w).
Como se trabaja desde un punto de vista estocástico, se introducirá en el análisis una variable aleatoria (ξ), que se definirá como la edad de cierre de una empresa recién creada.
Sea, l x el número de empresas sobrevivientes a la edad x, siendo l 0 el colectivo inicial, que en este caso serán 100 000 (empresas recién creadas).
El número de empresas cerradas a la edad x se denota como d x , en donde:
Sea, S(x) la función de supervivencia, que no es más que la probabilidad de que una empresa recién creada llegue con vida a la edad x. En términos más técnicos se dice que:
Siendo así, S(x) será igual a:
Por tanto, el número de empresas sobrevivientes a la edad x se puede calcular de la siguiente manera:
En este punto, es necesario denotar los siguientes criterios:
A medida que la edad de la empresa tiende a 0, la función de supervivencia S(x) tenderá a 1. Por tanto,
𝑆(0) = 1
A medida que la edad de la empresa tiende a w (límite superior de supervivencia), la función de supervivencia S(x) tenderá a 0.
𝑆(𝑤) = 0
La función de distribución se denota como F(x), que hace referencia a la probabilidad de que una empresa recién creada cierre antes de cumplir la edad x o menos. Técnicamente es:
Por tanto, se dirá que:
En este punto se obtienen algunas conclusiones de la función de distribución:
Por tanto,
𝐹(0) = 0
A medida que la edad de la empresa tiende a w (límite superior de supervivencia), la función de distribución F(x) tenderá a 1.
𝐹(𝑤) = 1
Si se requiere calcular las probabilidades de cierre de una empresa recién creada que esté entre las edades x y la edad x+t, se procederá de la siguiente manera:
Para calcular la probabilidad de fallecimiento/cierre/quiebra para cualquier edad, es necesario introducir al análisis el concepto de probabilidad condicional, que en el contexto del presente análisis será:
De la expresión anterior, se puede concluir la siguiente situación: es la probabilidad de que una empresa recién creada cierre entre las edades x y x+t, dado que ya tiene x años.
De manera análoga, se definirán las siguientes probabilidades:
t q x = probabilidad de que una empresa de edad x cierre dentro de los próximos t años.
Formalmente, esta probabilidad se expresa de la siguiente manera:
Que, como ya se dedujo, será igual a:
t P x = probabilidad de que una empresa de edad x sobreviva t años más.
Esta probabilidad es el complemento de t q x , por tanto:
t / n q x = probabilidad de que una empresa de edad x sobreviva t años más, y de que fallezca dentro de los próximos n años.
Formalmente, esta probabilidad se expresa de la siguiente manera:
La fuerza de mortalidad o tanto instantáneo de mortalidad. μx se definirá como la tasa a la cual comienza a crecer la mortalidad a partir de la edad x.
Técnicamente se define de la siguiente manera:
Como
Por lo tanto.
En donde:
La fuerza de mortalidad desde el punto de vista discreto será igual a:
Donde:
Ln es el logaritmo natural.
l (x-1) es el número de empresas sobrevivientes en el periodo anterior.
l (x+1) es el número de empresas sobrevivientes en el siguiente periodo.
La esperanza de vida ex el valor medio de la cantidad de años que vive una determinada población absoluta o total en un cierto periodo (Promislow, 2015).
Técnicamente se define de la siguiente manera:
Donde:
e x es la esperanza de vida abreviada.
kPx es la probabilidad que una empresa de x años llegue con vida a la edad x+k.
4. Resultados
4.1 Dinámica empresarial
En cuanto a la estructura y análisis de data, el análisis cuantitativo se realizó con base en información de Supercias (2019). Se trabajó con un total de 17 180 empresas (activas y cerradas), en el período 1901-2018. Esta información se observa en la Figura 1.

Fuente: elaboración propia a partir de Supercias (2019).
Figura 1 Total de empresas clasificadas por situación legal
En la Tabla 1 se observa la clasificación de empresas por la situación legal de los 24 sectores que componen la industria manufacturera, que de acuerdo con la clasificación industrial internacional uniforme (CIIU) pertenecen a la sección “C”. El 37,75 % corresponde a empresas activas y el restante 62,25 %, a cerradas.
Tabla 1 Situación legal empresarial por sector (C10-C33)
| CIIU | Situación legal | Total | |||
| Activa | Participación | Cerrada | Participación | ||
| C10 | 1256 | 39,31 % | 1939 | 60,69 % | 3195 |
| C11 | 226 | 35,87 % | 404 | 64,13 % | 630 |
| C12 | 5 | 31,25 % | 11 | 68,75 % | 16 |
| C13 | 258 | 32,01 % | 548 | 67,99 % | 806 |
| C14 | 392 | 30,32 % | 901 | 69,68 % | 1293 |
| C15 | 103 | 34,45 % | 196 | 65,55 % | 299 |
| C16 | 132 | 20,59 % | 509 | 79,41 % | 641 |
| C17 | 144 | 42,48 % | 195 | 57,52 % | 339 |
| C18 | 348 | 39,82 % | 526 | 60,18 % | 874 |
| C19 | 51 | 43,59 % | 66 | 56,41 % | 117 |
| C20 | 565 | 40,82 % | 819 | 59,18 % | 1384 |
| C21 | 243 | 41,82 % | 338 | 58,18 % | 581 |
| C22 | 362 | 43,72 % | 466 | 56,28 % | 828 |
| C23 | 254 | 31,83 % | 544 | 68,17 % | 798 |
| C24 | 115 | 34,64 % | 217 | 65,36 % | 332 |
| C25 | 365 | 38,18 % | 591 | 61,82 % | 956 |
| C26 | 113 | 36,81 % | 194 | 63,19 % | 307 |
| C27 | 130 | 40,88 % | 188 | 59,12 % | 318 |
| C28 | 218 | 33,49 % | 433 | 66,51 % | 651 |
| C29 | 118 | 40,27 % | 175 | 59,73 % | 293 |
| C30 | 70 | 36,46 % | 122 | 63,54 % | 192 |
| C31 | 191 | 29,84 % | 449 | 70,16 % | 640 |
| C32 | 153 | 32,90 % | 312 | 67,10 % | 465 |
| C33 | 673 | 54,94 % | 552 | 45,06 % | 1225 |
| Total | 6485 | 37,75 % | 10 695 | 62,25 % | 17 180 |
Fuente: elaboración propia a partir de Supercias (2019).
En la Tabla 2 se presenta el estado legal de las empresas de acuerdo con la provincia a la cual pertenecen. Se puede evidenciar que hay tres provincias en donde hay mayor dinamismo empresarial: Pichincha, Guayas y Azuay.
Tabla 2 Situación legal empresarial por provincia
| Provincia | Situación legal | Total | |||
| Activa | Participación | Cerrada | Participación | ||
| Azuay | 384 | 41,07 % | 551 | 58,93 % | 935 |
| Bolívar | 5 | 45,45 % | 6 | 54,55 % | 11 |
| Cañar | 17 | 42,50 % | 23 | 57,50 % | 40 |
| Carchi | 9 | 40,91 % | 13 | 59,09 % | 22 |
| Chimborazo | 33 | 28,95 % | 81 | 71,05 % | 114 |
| Cotopaxi | 48 | 51,61 % | 45 | 48,39 % | 93 |
| El Oro | 91 | 35,14 % | 168 | 64,86 % | 259 |
| Esmeraldas | 47 | 47,47 % | 52 | 52,53 % | 99 |
| Galápagos | 6 | 50,00 % | 6 | 50,00 % | 12 |
| Guayas | 2716 | 34,59 % | 5135 | 65,41 % | 7851 |
| Imbabura | 57 | 39,86 % | 86 | 60,14 % | 143 |
| Loja | 66 | 39,76 % | 100 | 60,24 % | 166 |
| Los Ríos | 47 | 40,87 % | 68 | 59,13 % | 115 |
| Manabí | 275 | 46,61 % | 315 | 53,39 % | 590 |
| Morona Santiago | 4 | 25,00 % | 12 | 75,00 % | 16 |
| Napo | 7 | 63,64 % | 4 | 36,36 % | 11 |
| Orellana | 23 | 58,97 % | 16 | 41,03 % | 39 |
| Pastaza | 6 | 37,50 % | 10 | 62,50 % | 16 |
| Pichincha | 2309 | 39,07 % | 3601 | 60,93 % | 5910 |
| Santa Elena | 48 | 50,00 % | 48 | 50,00 % | 96 |
| Santo Domingo de los Tsáchilas | 51 | 43,59 % | 66 | 56,41 % | 117 |
| Sucumbíos | 49 | 53,26 % | 43 | 46,74 % | 92 |
| Tungurahua | 185 | 43,12 % | 244 | 56,88 % | 429 |
| Zamora Chinchipe | 2 | 50,00 % | 2 | 50,00 % | 4 |
| Total general | 6485 | 10 695 | 17 180 | ||
Fuente: elaboración propia a partir de Supercias (2019).
Las empresas grandes presentan una mayor proporción de empresas cerradas (74,33 %), seguidas de las medianas (69,76 %), las pequeñas (64,93 %) y las microempresas (54,39 %) (ver Tabla 3).
Tabla 3 Situación legal empresarial por tamaño (C10-C33)
| Tamaño | Situación legal | Total | |||
| Activas | Participación | Cerradas | Participación | ||
| Grande | 371 | 25,67 % | 1074 | 74,33 % | 1445 |
| Mediana | 812 | 30,24 % | 1873 | 69,76 % | 2685 |
| Pequeña | 2163 | 35,07 % | 4005 | 64,93 % | 6168 |
| Microempresa | 3139 | 45,61 % | 3743 | 54,39 % | 6882 |
| Total | 6485 | 10 695 | 17 180 | ||
Fuente: elaboración propia a partir de la Supercias (2019).
4.1.1 Demografía empresarial del sector de manufactura
En el sector de manufactura se crearon 17 180 empresas en el periodo 1901-2018, a finales del 2018 se encontraban activas 37,74 %, las demás estaban inactivas o en procesos de disolución, liquidación o cancelación (ver Tabla 4).
Tabla 4 Situación legal de las empresas, periodo 1901-2018
| Situación legal | Cantidad de empresas | % |
| Activa | 6484 | 37,74 % |
| Cancelación de inscripción anotada en RM | 5473 | 31,86 % |
| Disolución y liquidación | 4603 | 26,79 % |
| Liquidación en pleno derecho | 86 | 0,50 % |
| Inactiva | 534 | 3,11 % |
| Total | 17 180 | 100,00 % |
Fuente: elaboración propia a partir de la Supercias (2019).
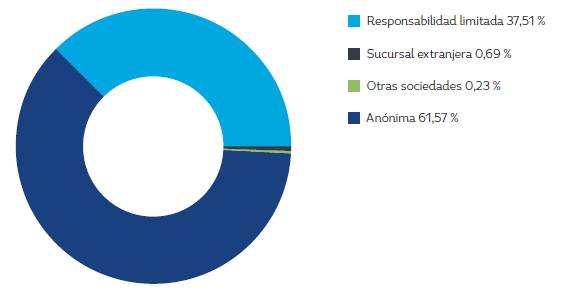
Según la creación de empresas por tipo de sociedad, el 61,57 % correspondió a sociedades anónimas; el 37,51 %, a responsabilidad limitada; el 0,69 %, a sucursal extranjera y el 0,23 % pertenece a otros tipos de sociedades (ver Figura 2).
4.1.2 Creación de empresas
En los últimos cuarenta años, se ha observado una tendencia creciente con relación al número de empresas creadas, siendo el 2015 el año en el cual se presenta el pico más alto con 700 empresas nuevas (ver Figura 3).
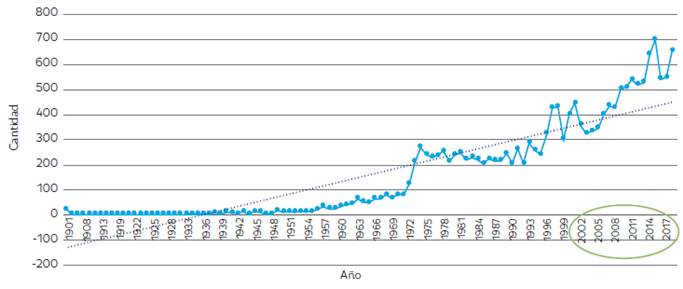
Fuente: elaboración propia a partir de Supercias (2019).
Figura 3 Crecimiento empresarial por número de empresas por año
El sector de manufactura ha estado en un constante crecimiento; sin embargo, las tasas indican en términos relativos que el ritmo con el que se crean empresas se está desacelerando. En la Figura 4 se observa que en el periodo 1901-2018 hubo una tasa promedio de nacimiento del 6,5 %, el año máximo de crecimiento corresponde a 1973 con el 19,4 %. Al revisar el periodo 2000-2018, la tendencia de crecimiento bajó a 4,1 %, lo que está por debajo del promedio general. La desviación estándar del 3,53 % en una tasa promedio de 6,5 % da una volatilidad de 0,54, siendo más volátil en los primeros años de historia empresarial de Ecuador.

Fuente: elaboración propia a partir de Supercias (2019).
Figura 4 Tasa anual de crecimiento empresarial
En la Figura 5 se observa que a partir de 1990 las sociedades anónimas experimentan un mayor crecimiento, seguidas de las empresas de responsabilidad limitada.
4.1.3 Tasa neta de crecimiento y rotación empresarial
Como se ve en la Tabla 5, la dinámica empresarial por tipo de empresa indica que el 59,21 % de las empresas cerradas corresponde a sociedades anónimas, mientras que el 39,99 %, a responsabilidad limitada. La participación de las sociedades anónimas crece en el total de empresas, y pasa del 61,57 % de tasa de creación al 65,41 % de empresas activas del total general. Además, del total de empresas activas al 2018, el 65, 41 % corresponde a sociedades anónimas, mientras que las de responsabilidad limitada son el 33,48 %; otras formas de asociación empresarial representan el 1,11 %.
Tabla 5 Distribución porcentual de la demografía empresarial de acuerdo con su situación legal en el periodo 1901 -2018
| Tipo de compañía | Nacimiento | Cierre | Activas | |||
| Anónima | 10 578 | 61,57 % | 6290 | 59,21 % | 4288 | 65,41 % |
| Anónima de desarrollo agropecuario | 1 | 0,01 % | 1 | 0,01 % | 0 | 0,00 % |
| Anónima multinacional andina | 3 | 0,02 % | 2 | 0,02 % | 1 | 0,02 % |
| Asociación o consorcio | 5 | 0,03 % | 2 | 0,02 % | 3 | 0,05 % |
| Comandita por acciones | 1 | 0,01 % | 1 | 0,01 % | 0 | 0,00 % |
| Economía mixta | 30 | 0,17 % | 23 | 0,22 % | 7 | 0,11 % |
| Responsabilidad limitada | 6444 | 37,51 % | 4249 | 39,99 % | 2195 | 33,48 % |
| Sucursal extranjera | 118 | 0,69 % | 56 | 0,53 % | 62 | 0,95 % |
| Total | 17 180 | 10 624 | 6556 | |||
Fuente: elaboración propia a partir de Supercias (2019).
Al relacionar el tamaño empresarial con la dinámica entre el porcentaje de empresas que nacen con empresas cerradas y activas, se evidencia que las empresas grandes pierden participación dentro del total de empresas y bajan del 1,44 % al 1,32 % de activas; de igual forma, las medianas bajan del 7,92 % al 7,15 % de activas; por lo contrario, las microempresas ganan participación con un 62,31 % de total general al 2018 (ver Tabla 6).
Tabla 6 Distribución porcentual de la demografía empresarial de acuerdo al tamaño de las empresas
| Tamaño | Creación | Cerradas | Activas |
| Grande | 94 | 39 | 55 |
| Mediana | 518 | 219 | 299 |
| Pequeña | 1908 | 687 | 1221 |
| Microempresa | 4020 | 1416 | 2604 |
| Total general | 6540 | 2361 | 4179 |
| Grande | 1,44 % | 1,65 % | 1,32 % |
| Mediana | 7,92 % | 9,28 % | 7,15 % |
| Pequeña | 29,17 % | 29,10 % | 29,22 % |
| Microempresa | 61,47 % | 59,97 % | 62,31 % |
| Total general | 100,00 % | 100,00 % | 100,00 % |
Fuente: elaboración propia a partir de Supercias (2019).
En el tiempo analizado, se llega a demostrar que la estructura de empresas dividida por tamaño mantiene su tendencia: presenta una mayor participación de microempresas y una menor de empresas grandes. Con respecto al número de empresas, es mucho más el impacto del cierre de las micro y pequeñas empresas, porque del total de mortalidad corresponde al 59,97 % y al 29,10 % respectivamente, lo que genera un total de 89,07 % (ver Tabla 7).
Tabla 7 Edad promedio empresarial según el tamaño
| Detalle | Peso del total | Empresas iniciadas | Empresas Cerradas | % | Empresas Activas | Edad ( en años) | Peso Activas | Peso Cerradas | ||
| Promedio activas | Promedio cerradas | Promedio total | ||||||||
| Grande | 1,32 % | 94 | 39 | 1,65 % | 55 | 9,45 | 5,26 | 7,71 | 58,51 % | 41,49 % |
| Mediana | 7,15 % | 518 | 219 | 9,28 % | 299 | 8,04 | 5,01 | 6,76 | 57,72 % | 42,28 % |
| Microempresa | 62,31 % | 4020 | 1416 | 59,97 % | 2604 | 5,34 | 4,28 | 4,97 | 64,78 % | 35,22 % |
| Pequeña | 29,22 % | 1908 | 687 | 29,10 % | 1221 | 6,96 | 4,87 | 6,21 | 63,99 % | 36,01 % |
| Total | 100,00 % | 6540 | 2361 | 4179 | 6,06 | 4,54 | 5,51 | 63,90 % | 36,10 % | |
Fuente: elaboración propia a partir de Supercias (2019).
El impacto del cierre de las micro y pequeñas empresas se relaciona también con la transición empresarial, en la que de acuerdo con el Instituto Nacional de Estadística y Censos (2019), en su estudio sobre la dinámica laboral y empresarial del panorama laboral, 2017, las mipymes son las que más movilidad tienen, puesto que pocas empresas mantienen el mismo tamaño entre el 2009 y el 2015. De hecho, el 25,8 % de microempresas, el 48,2 % de empresas pequeñas y el 58 % de medianas mantienen su tamaño durante el periodo analizado, mientras que el 19,6 % de las microempresas activas en 2009 crecieron a pequeñas empresas en 2015 y apenas el 1,1 % de estas empresas creció a empresas medianas o grandes.
4.1.4. Demografía, tasas netas
En la Figura 6 se puede ver que la tasa de natalidad empresarial cada vez es mayor, en la antigüedad se creaban una o dos empresas por año, mientras que al 2018 se llegó a contar con cerca de 600 empresas nuevas cada año. También se observa que estas empresas duran cada vez menos tiempo, y llegan a cerrar en promedio en tres años.
En la Tabla 8 se analizan intervalos de 10 años, en los que se observa que la creación de empresas es cada vez mayor. Sin embargo, lo preocupante es que las empresas duran menos tiempo (existe una alta rotación); por ejemplo, en el último intervalo, 2009-2018, 4886 empresas de 5678 fueron cerradas, es decir, un 88,05 %. Además, se observa que a medida que pasa el tiempo las empresas tienen una probabilidad de vida más corta, hace 50 años era de 32 años y ha ido bajando hasta llegar a un promedio de 3 años.
Tabla 8 Distribución en intervalos de 10 años de tasas de crecimiento y de rotación
| Intervalo anual | Empresas creadas | Empresas cerradas por año de cierre | Crecimiento promedio | Cierre promedio (rotación) | Edad promedio cerradas | |
| 1899 | 1908 | 25 | 4,26% | 90,59 | ||
| 1909 | 1918 | 5 | 3,65% | 90,20 | ||
| 1919 | 1928 | 18 | 4,70% | 65,72 | ||
| 1929 | 1938 | 27 | 1 | 5,61% | 0,20% | 44,77 |
| 1939 | 1948 | 69 | 1 | 6,60% | 0,09% | 48,03 |
| 1949 | 1958 | 169 | 2 | 7,85% | 0,08% | 41,28 |
| 1959 | 1968 | 512 | 7 | 9,80% | 0,12% | 32,45 |
| 1969 | 1978 | 1793 | 33 | 11,71% | 0,21% | 24,47 |
| 1979 | 1988 | 2231 | 342 | 6,35% | 0,85% | 18,31 |
| 1989 | 1998 | 2882 | 1781 | 5,91% | 3,71% | 13,17 |
| 1999 | 2008 | 3771 | 3571 | 6,29% | 5,93% | 8,21 |
| 2009 | 2018 | 5678 | 4886 | 8,78% | 7,50% | 3,03 |
| Total | 17180 | 10624 | 6,79% | 2,08% | ||
| Desviación | 0,024 | 0,029 | ||||
| Coeficiente de variación | 0,349 | 1,394 | ||||
Fuente: elaboración propia a partir de la Supercias (2019).
En la Figura 7 se presenta el comportamiento de las empresas manufactureras en intervalos de 10 años (empresas creadas, activas y cerradas), y en la que se aprecia que en los últimos 40 años existe una mayor actividad demográfica empresarial.

Fuente: elaboración propia a partir de Supercias (2019).
Figura 7 Tendencia de edad, empresas creadas, activas y cerradas tomando como base el año de creación en el periodo 1901-2018
Del 2000 a 2018 la tasa de natalidad presenta una mayor estabilidad con un crecimiento promedio del 7,65 % y una menor volatilidad de aproximadamente 0,23 %, mientras que las empresas que se cierran y la tasa de mortandad o rotación presentan una alta variabilidad (desviación) del 5,5 % de una tasa de cierre promedio de 6,82 %, lo que hace muy volátil el cierre empresarial con un coeficiente del 0,81. Igualmente, se evidencia una tasa de variación neta (creación menos destrucción) promedio del 0,82 %, con un valor máximo en el año 2015 de 7,79 %, mientras que para el año 2006 esta tasa es de -16,25 %. El estancamiento económico evidenciado en los años 2016, 2017 y 2018 ha provocado una disminución de empresas en 128, 36 y 112 respectivamente (ver Tabla 9).
Tabla 9 Determinación de las tasas de natalidad, rotación y crecimiento neto
| Año Creación | Empresas Creadas | Año cierre | Empresas Ceradas | Empresas neto | Tasa de natalidad | % rotación R=S/((I+F)/2) (mortandad) | Crecimiento Neto |
| 2000 | 401 | 2000 | 141 | 5866 | 6,99% | 2,46% | 4,53% |
| 2001 | 445 | 2001 | 53 | 6258 | 7,34% | 0,87% | 6,47% |
| 2002 | 359 | 2002 | 78 | 6539 | 5,61% | 1,22% | 4,39% |
| 2003 | 325 | 2003 | 129 | 6735 | 4,90% | 1,94% | 2,95% |
| 2004 | 333 | 2004 | 477 | 6591 | 5,00% | 7,16% | -2,16% |
| 2005 | 345 | 2005 | 587 | 6349 | 5,33% | 9,07% | -3,74% |
| 2006 | 400 | 2006 | 1352 | 5397 | 6,81% | 23,02% | -16,25% |
| 2007 | 434 | 2007 | 291 | 5540 | 7,94% | 5,32% | 2,62% |
| 2008 | 428 | 2008 | 204 | 5764 | 7,57% | 3,61% | 3,96% |
| 2009 | 501 | 2009 | 167 | 6098 | 8,45% | 2,82% | 5,63% |
| 2010 | 508 | 2010 | 422 | 6184 | 8,27% | 6,87% | 1,40% |
| 2011 | 540 | 2011 | 212 | 6512 | 8,51% | 3,34% | 5,17% |
| 2012 | 518 | 2012 | 565 | 6465 | 7,98% | 8,71% | -0,72% |
| 2013 | 529 | 2013 | 318 | 6676 | 8,05% | 4,84% | 3,21% |
| 2014 | 639 | 2014 | 995 | 6320 | 9,83% | 15,31% | -5,48% |
| 2015 | 700 | 2015 | 188 | 6832 | 10,64% | 2,86% | 7,79% |
| 2016 | 541 | 2016 | 669 | 6704 | 7,99% | 9,88% | -1,89% |
| 2017 | 549 | 2017 | 585 | 6668 | 8,21% | 8,75% | -0,54% |
| 2018 | 653 | 2018 | 765 | 6556 | 9,88% | 11,57% | -1,69% |
| Promedio | 481,47 | 431,47 | 7,65% | 6,82% | 0,82% | ||
| Desviación | 110,03 | 342,06 | 1,61% | 5,52% | 5,53% | ||
| Volatilidad | 0,23 | 0,79 | 0,21 | 0,81 | 6,72 |
Fuente: elaboración propia a partir de Supercias (2019).
Para encontrar los indicadores de rotación de las empresas, se utilizó la siguiente fórmula:
Donde:
R= tasa de rotación, S= empresas cerradas en el periodo, I= empresas que estaban al inicio del periodo, F= empresas que se tenía al final del periodo.
4.1.5 Supervivencia empresarial
Al analizar la supervivencia empresarial, se muestra que de las empresas que se crearon en el año 2007 el 97,00 % permanecieron funcionando en el tercer año, mientras que, de las empresas creadas en el año 2015, el 68,86 % sobrevivieron al tercer año (ver Tabla 10).
Tabla 10 Determinación histórica de supervivencia empresarial del sector manufacturero de Ecuador en función del año de creación
| Años | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Promedio |
| 1 | 99,77 % | 100,00 % | 99,60 % | 99,61 % | 100,00% | 99,81 % | 98,87 % | 99,37 % | 99,29 % | 99,08 % | 98,18 % | 99,69 % | 99,44 % |
| 2 | 98,39 % | 98,83 % | 99,00 % | 99,21 % | 99,26% | 85,14 % | 95,27 % | 93,74 % | 89,00 % | 82,99 % | 97,45 % | 94,39 % | |
| 3 | 97,00 % | 96,96 % | 83,63 % | 88,19 % | 76,11% | 83,20 % | 75,43 % | 80,75 % | 68,86 % | 82,44 % | 83,26 % | ||
| 4 | 95,39 % | 80,84 % | 76,65 % | 66,73 % | 74,44% | 69,31 % | 67,11 % | 68,54 % | 68,71 % | 74,19 % | |||
| 5 | 80,18 % | 76,40 % | 62,87 % | 64,76 % | 62,04% | 60,81 % | 60,49 % | 67,29 % | 66,86 % | ||||
| 6 | 74,42 % | 64,25 % | 60,88 % | 54,92 % | 56,30% | 54,83 % | 60,11 % | 60,82 % | |||||
| 7 | 58,53 % | 60,75 % | 54,49 % | 47,83 % | 50,74% | 54,05 % | 54,40 % | ||||||
| 8 | 55,99 % | 52,57 % | 50,30 % | 41,73 % | 50,19% | 50,16 % | |||||||
| 9 | 50,23 % | 48,13 % | 42,91 % | 40,94 % | 45,56 % | ||||||||
| 10 | 47,24 % | 42,06 % | 42,71 % | 44,00 % | |||||||||
| 11 | 39,17 % | 41,12 % | 40,15 % | ||||||||||
| 12 | 38,94 % | 38,94 % |
Fuente: elaboración propia a partir de Supercias (2019).
El desempeño de una economía no solo depende del flujo de entrada y salida de empresas, sino también de cuán capaces son de perdurar en el tiempo. La probabilidad de que una empresa creada entre 2000 y 2018 siga en funcionamiento luego de tres años es del 83,26 %, y la probabilidad de que sobreviva 6 años es del 60,82 %. El índice de riesgo de mortalidad llega al máximo en los primeros años debido a procesos de aprendizaje (ver Figura 8).

Fuente: elaboración propia a partir de Supercias (2019).
Figura 8 Probabilidad promedio de supervivencia empresarial del sector manufacturero de Ecuador
En la Figura 9 se observa que por cada 1 % de empresas que nacen el 0,49 % cierran.
5. Resultados obtenidos del modelo de tabla de mortalidad empresarial
La edad de las empresas analizadas en la tabla de mortalidad (Tabla 11 y Tabla 12) está entre 0 y 106 años.
Tabla 11 Tabla de cierre empresarial
| x | Cantidad de empresas cerrdadas (dx) | Empresas sobrevivientes (lx) | Función de supervivencia ( Sx) | Función de distribución (Fx) | Probabilidad anual de supervivencia ( Px) | Probabilidad anual de cierre ( qx) | Fuerza de mortalidad ( μx) | Esperanza de vida ( ex) |
| 0 | 94 | 100 000 | 1,000 | 0,000 | 0,999 | 0,001 | 14,275 | |
| 1 | 431 | 99 906 | 0,999 | 0,001 | 0,996 | 0,004 | 0,003 | 13,288 |
| 2 | 3483 | 99 476 | 0,995 | 0,005 | 0,965 | 0,035 | 0,020 | 12,346 |
| 3 | 6610 | 95 993 | 0,960 | 0,040 | 0,931 | 0,069 | 0,053 | 11,794 |
| 4 | 5768 | 89 382 | 0,894 | 0,106 | 0,935 | 0,065 | 0,069 | 11,666 |
| 5 | 5337 | 83 614 | 0,836 | 0,164 | 0,936 | 0,064 | 0,066 | 11,470 |
| 6 | 4860 | 78 277 | 0,783 | 0,217 | 0,938 | 0,062 | 0,065 | 11,253 |
| 7 | 4700 | 73 418 | 0,734 | 0,266 | 0,936 | 0,064 | 0,065 | 10,997 |
| 8 | 5337 | 68 717 | 0,687 | 0,313 | 0,922 | 0,078 | 0,074 | 10,750 |
| 9 | 4803 | 63 380 | 0,634 | 0,366 | 0,924 | 0,076 | 0,080 | 10,655 |
| 10 | 3942 | 58 577 | 0,586 | 0,414 | 0,933 | 0,067 | 0,074 | 10,528 |
| 11 | 4176 | 54 635 | 0,546 | 0,454 | 0,924 | 0,076 | 0,075 | 10,288 |
| 12 | 4073 | 50 459 | 0,505 | 0,495 | 0,919 | 0,081 | 0,082 | 10,140 |
| 13 | 3783 | 46 386 | 0,464 | 0,536 | 0,918 | 0,082 | 0,085 | 10,030 |
| 14 | 3876 | 42 603 | 0,426 | 0,574 | 0,909 | 0,091 | 0,090 | 9,920 |
| 15 | 3549 | 38 727 | 0,387 | 0,613 | 0,908 | 0,092 | 0,096 | 9,913 |
| 16 | 3099 | 35 178 | 0,352 | 0,648 | 0,912 | 0,088 | 0,094 | 9,913 |
| 17 | 3296 | 32 079 | 0,321 | 0,679 | 0,897 | 0,103 | 0,100 | 9,871 |
| 18 | 2425 | 28 783 | 0,288 | 0,712 | 0,916 | 0,084 | 0,098 | 10,002 |
| 19 | 2509 | 26 358 | 0,264 | 0,736 | 0,905 | 0,095 | 0,094 | 9,922 |
| 20 | 2116 | 23 848 | 0,238 | 0,762 | 0,911 | 0,089 | 0,096 | 9,966 |
| 21 | 2032 | 21 732 | 0,217 | 0,783 | 0,907 | 0,093 | 0,096 | 9,936 |
| 22 | 1826 | 19 700 | 0,197 | 0,803 | 0,907 | 0,093 | 0,098 | 9,961 |
| 23 | 1442 | 17 875 | 0,179 | 0,821 | 0,919 | 0,081 | 0,091 | 9,979 |
| 24 | 1536 | 16 433 | 0,164 | 0,836 | 0,907 | 0,093 | 0,091 | 9,854 |
| 25 | 1470 | 14 897 | 0,149 | 0,851 | 0,901 | 0,099 | 0,101 | 9,870 |
| 26 | 1236 | 13 427 | 0,134 | 0,866 | 0,908 | 0,092 | 0,100 | 9,950 |
| 27 | 1245 | 12 191 | 0,122 | 0,878 | 0,898 | 0,102 | 0,102 | 9,959 |
| 28 | 955 | 10 946 | 0,109 | 0,891 | 0,913 | 0,087 | 0,100 | 10,092 |
| 29 | 908 | 9991 | 0,100 | 0,900 | 0,909 | 0,091 | 0,093 | 10,057 |
| 30 | 993 | 9082 | 0,091 | 0,909 | 0,891 | 0,109 | 0,106 | 10,063 |
| 31 | 777 | 8090 | 0,081 | 0,919 | 0,904 | 0,096 | 0,108 | 10,297 |
| 32 | 702 | 7313 | 0,073 | 0,927 | 0,904 | 0,096 | 0,101 | 10,392 |
| 33 | 581 | 6610 | 0,066 | 0,934 | 0,912 | 0,088 | 0,096 | 10,496 |
| 34 | 478 | 6030 | 0,060 | 0,940 | 0,921 | 0,079 | 0,087 | 10,506 |
| 35 | 487 | 5552 | 0,056 | 0,944 | 0,912 | 0,088 | 0,087 | 10,410 |
| 36 | 356 | 5066 | 0,051 | 0,949 | 0,930 | 0,070 | 0,082 | 10,410 |
| 37 | 478 | 4710 | 0,047 | 0,953 | 0,899 | 0,101 | 0,090 | 10,197 |
| 38 | 440 | 4232 | 0,042 | 0,958 | 0,896 | 0,104 | 0,108 | 10,347 |
| 39 | 328 | 3792 | 0,038 | 0,962 | 0,914 | 0,086 | 0,100 | 10,548 |
| 40 | 365 | 3464 | 0,035 | 0,965 | 0,895 | 0,105 | 0,101 | 10,546 |
| 41 | 346 | 3099 | 0,031 | 0,969 | 0,888 | 0,112 | 0,115 | 10,789 |
| 42 | 225 | 2753 | 0,028 | 0,972 | 0,918 | 0,082 | 0,102 | 11,146 |
| 43 | 225 | 2528 | 0,025 | 0,975 | 0,911 | 0,089 | 0,089 | 11,137 |
| 44 | 281 | 2303 | 0,023 | 0,977 | 0,878 | 0,122 | 0,112 | 11,224 |
| 45 | 197 | 2022 | 0,020 | 0,980 | 0,903 | 0,097 | 0,116 | 11,782 |
| 46 | 140 | 1826 | 0,018 | 0,982 | 0,923 | 0,077 | 0,091 | 12,051 |
| 47 | 122 | 1685 | 0,017 | 0,983 | 0,928 | 0,072 | 0,078 | 12,056 |
| 48 | 112 | 1564 | 0,016 | 0,984 | 0,928 | 0,072 | 0,075 | 11,994 |
| 49 | 84 | 1451 | 0,015 | 0,985 | 0,942 | 0,058 | 0,067 | 11,923 |
| 50 | 122 | 1367 | 0,014 | 0,986 | 0,911 | 0,089 | 0,077 | 11,658 |
| 51 | 131 | 1245 | 0,012 | 0,988 | 0,895 | 0,105 | 0,102 | 11,797 |
| 52 | 103 | 1114 | 0,011 | 0,989 | 0,908 | 0,092 | 0,104 | 12,185 |
| 53 | 66 | 1011 | 0,010 | 0,990 | 0,935 | 0,065 | 0,082 | 12,426 |
Tabla 12 Tabla de cierre empresarial (continuación)
| x | Cantidad de empresas cerrdadas (dx) | Empresas sobrevivientes (lx) | Función de supervivencia ( Sx) | Función de distribución (Fx) | Probabilidad anual de supervivencia ( Px) | Probabilidad anual de cierre ( qx) | Fuerza de mortalidad ( μx) | Esperanza de vida (ex) |
| 54 | 66 | 946 | 0,009 | 0,991 | 0,931 | 0,069 | 0,069 | 12,287 |
| 55 | 75 | 880 | 0,009 | 0,991 | 0,915 | 0,085 | 0,080 | 12,202 |
| 56 | 75 | 805 | 0,008 | 0,992 | 0,907 | 0,093 | 0,093 | 12,337 |
| 57 | 56 | 730 | 0,007 | 0,993 | 0,923 | 0,077 | 0,089 | 12,603 |
| 58 | 66 | 674 | 0,007 | 0,993 | 0,903 | 0,097 | 0,091 | 12,653 |
| 59 | 56 | 609 | 0,006 | 0,994 | 0,908 | 0,092 | 0,100 | 13,015 |
| 60 | 37 | 552 | 0,006 | 0,994 | 0,932 | 0,068 | 0,084 | 13,339 |
| 61 | 84 | 515 | 0,005 | 0,995 | 0,836 | 0,164 | 0,124 | 13,309 |
| 62 | 84 | 431 | 0,004 | 0,996 | 0,804 | 0,196 | 0,198 | 14,913 |
| 63 | 47 | 346 | 0,003 | 0,997 | 0,865 | 0,135 | 0,181 | 17,541 |
| 64 | 28 | 300 | 0,003 | 0,997 | 0,906 | 0,094 | 0,122 | 19,281 |
| 65 | 19 | 272 | 0,003 | 0,997 | 0,931 | 0,069 | 0,085 | 20,276 |
| 66 | 9 | 253 | 0,003 | 0,997 | 0,963 | 0,037 | 0,055 | 20,778 |
| 67 | 0 | 243 | 0,002 | 0,998 | 1,000 | 0,000 | 0,019 | 20,577 |
| 68 | 28 | 243 | 0,002 | 0,998 | 0,885 | 0,115 | 0,061 | 19,577 |
| 69 | 0 | 215 | 0,002 | 0,998 | 1,000 | 0,000 | 0,061 | 21,130 |
| 70 | 0 | 215 | 0,002 | 0,998 | 1,000 | 0,000 | 0,000 | 20,130 |
| 71 | 19 | 215 | 0,002 | 0,998 | 0,913 | 0,087 | 0,045 | 19,130 |
| 72 | 0 | 197 | 0,002 | 0,998 | 1,000 | 0,000 | 0,045 | 19,952 |
| 73 | 0 | 197 | 0,002 | 0,998 | 1,000 | 0,000 | 0,000 | 18,952 |
| 74 | 9 | 197 | 0,002 | 0,998 | 0,952 | 0,048 | 0,024 | 17,952 |
| 75 | 0 | 187 | 0,002 | 0,998 | 1,000 | 0,000 | 0,024 | 17,850 |
| 76 | 19 | 187 | 0,002 | 0,998 | 0,900 | 0,100 | 0,053 | 16,850 |
| 77 | 0 | 169 | 0,002 | 0,998 | 1,000 | 0,000 | 0,053 | 17,722 |
| 78 | 9 | 169 | 0,002 | 0,998 | 0,944 | 0,056 | 0,029 | 16,722 |
| 79 | 0 | 159 | 0,002 | 0,998 | 1,000 | 0,000 | 0,029 | 16,706 |
| 80 | 0 | 159 | 0,002 | 0,998 | 1,000 | 0,000 | 0,000 | 15,706 |
| 81 | 0 | 159 | 0,002 | 0,998 | 1,000 | 0,000 | 0,000 | 14,706 |
| 82 | 9 | 159 | 0,002 | 0,998 | 0,941 | 0,059 | 0,030 | 13,706 |
| 83 | 0 | 150 | 0,001 | 0,999 | 1,000 | 0,000 | 0,030 | 13,563 |
| 84 | 0 | 150 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 12,563 |
| 85 | 9 | 150 | 0,001 | 0,999 | 0,938 | 0,063 | 0,032 | 11,563 |
| 86 | 0 | 140 | 0,001 | 0,999 | 1,000 | 0,000 | 0,032 | 11,333 |
| 87 | 0 | 140 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 10,333 |
| 88 | 0 | 140 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 9,333 |
| 89 | 19 | 140 | 0,001 | 0,999 | 0,867 | 0,133 | 0,072 | 8,333 |
| 90 | 0 | 122 | 0,001 | 0,999 | 1,000 | 0,000 | 0,072 | 8,615 |
| 91 | 19 | 122 | 0,001 | 0,999 | 0,846 | 0,154 | 0,084 | 7,615 |
| 92 | 0 | 103 | 0,001 | 0,999 | 1,000 | 0,000 | 0,084 | 8,000 |
| 93 | 9 | 103 | 0,001 | 0,999 | 0,909 | 0,091 | 0,048 | 7,000 |
| 94 | 19 | 94 | 0,001 | 0,999 | 0,800 | 0,200 | 0,159 | 6,700 |
| 95 | 0 | 75 | 0,001 | 0,999 | 1,000 | 0,000 | 0,112 | 7,375 |
| 96 | 0 | 75 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 6,375 |
| 97 | 19 | 75 | 0,001 | 0,999 | 0,750 | 0,250 | 0,144 | 5,375 |
| 98 | 0 | 56 | 0,001 | 0,999 | 1,000 | 0,000 | 0,144 | 6,167 |
| 99 | 0 | 56 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 5,167 |
| 100 | 0 | 56 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 4,167 |
| 101 | 0 | 56 | 0,001 | 0,999 | 1,000 | 0,000 | 0,000 | 3,167 |
| 102 | 9 | 56 | 0,001 | 0,999 | 0,833 | 0,167 | 0,091 | 2,167 |
| 103 | 9 | 47 | 0,000 | 1,000 | 0,800 | 0,200 | 0,203 | 1,600 |
| 104 | 9 | 37 | 0,000 | 1,000 | 0,750 | 0,250 | 0,255 | 1,000 |
| 105 | 19 | 28 | 0,000 | 1,000 | 0,333 | 0,667 | 0,693 | 0,333 |
| 106 | 9 | 9 | 0,000 | 1,000 | 0,000 | 1,000 | 0,000 |
Fuente: elaboración propia a partir de Supercias (2019).
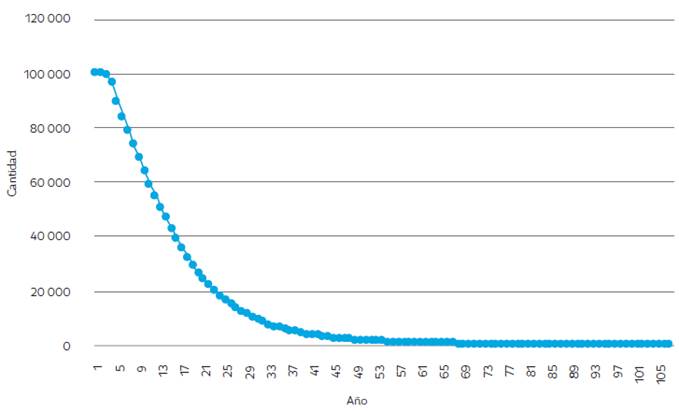
Partiendo del colectivo inicial de 100 000 empresas, se pueden mencionar los siguientes resultados: la columna del número de empresas cerradas muestra que el año en el que más empresas cerraron sus actividades es el tercero, con 6010 empresas; a partir de esta edad, el número de empresas cerradas cae. En este año la función de distribución es igual a un 4 % ( F(3)=4 %) , es decir, la probabilidad de la edad de cierre de una empresa recién creada a los 3 o menos años es de 4 %. Por lo tanto, la probabilidad de que una empresa recién creada sobreviva a la edad 3 es de un 96 %. (ver Figura 10).
Es evidente que el comportamiento del número de empresas cerradas por año condicionará el comportamiento del número de empresas sobrevivientes en un determinado año, cuyo comportamiento se observa en la Figura 11.
Al continuar con el análisis en el tercer año, se puede decir que la probabilidad de que una empresa con 3 años sobreviva un año más es de 93,1 %, por lo tanto, la probabilidad de que una empresa que tiene 3 años de vida cierre el siguiente año es de 6,9 %.
En la Figura 12 se observa el comportamiento de la serie de tiempo de la esperanza de vida de las empresas; muestra, además, un comportamiento diferente de lo que pasa con las personas, cuya esperanza de vida disminuye con la edad, no así en las empresas, en las que se puede dividir la serie es dos partes:
1. Una primera parte en forma de “u” desde x=0 a x=70.
2. Una segunda parte, después de x=70.
Con base en lo mencionado, se puede indicar lo siguiente:
1. La esperanza de vida de una empresa recién creada es de 14,275 años.
2. El punto más bajo de la serie de tiempo de la esperanza de vida en la primera parte es 9,87 años, que es la esperanza de vida para una empresa que ya tiene 24 años.
3. La esperanza de vida a la edad 70 años es el punto más alto de toda la serie de tiempo analizada con 21,13 años.
4. Después de los 70 años de vida de las empresas, su esperanza de vida tiende a caer.
En cuanto a la fuerza de moralidad, su comportamiento es muy variable (ver Figura 13). Pero lo se puede analizar en dos periodos:
1. De la edad 0 a 17, cuando la fuerza de mortalidad empresarial crece y llega a 0,10.
2. De 18 en adelante, cuando la fuerza de mortalidad empresarial tiene un comportamiento un tanto volátil debido a que en algunos años no hubo cierre empresarial y en otros hubo una gran cantidad de empresas cerradas.
6. Discusión
La explicación y predicción del cierre empresarial despierta interés en un amplio conjunto de agentes económicos, inversores, acreedores, clientes, instituciones financieras y la literatura aplicada al fracaso empresarial tiene un gran número de teorías para discriminar las empresas sanas de las fracasadas. En este trabajo se planteó un modelo de tabla de mortalidad empresarial basada en análisis de supervivencia del conjunto de empresas creadas y cerradas entre 1901 y 2018.
A diferencia de los estudios planteados para quiebra empresarial, propuestos mediante técnicas de estadística multivalente por FitzPatrick (1932), Beaver (1966), Altman (1968), Ohlson (1980)), y los que plantean el uso de redes neuronales, propuestos por Odom y Sharda (1990), Zhang et al. (1999), Ahn et al. (2000), Hua et al. (2007), Berg (2007)), Ghazali et al. (2009), se aplicaron técnicas actuariales para calcular la probabilidad de supervivencia al observar el fenómeno de cierre empresarial repetidas veces en el tiempo a través una tabla de mortalidad empresarial.
Los resultados obtenidos difieren con respecto a las teorías planteadas por Bruderl y Schussler (1990) y Henderson y Clark (1990), y convergen en cierta manera con el estudio planteado por Stinchcombe (1965), en el sentido de que existe un mayor número de empresas cerradas en los primeros años de vida, los resultados así lo demuestran: en el año tres de vida, existe un mayor número de cierres, pero este valor tiende a caer con el tiempo, a pesar de que la fuerza de mortalidad sea más o menos estable en el tiempo. De la misma manera, los resultados obtenidos son congruentes con Daepp et al. (2015), quienes mencionan que la tasa de riesgo permanece más o menos constante y que la media de vida de las empresas es de 10 años. En el caso de las empresas manufactureras ecuatorianas, se observa que la fuerza de mortalidad de las empresas es más o menos constante durante los 100 primeros años, y la esperanza de vida promedio es de 11,54 años independiente del subsector de manufacturas.
Lo que distingue el análisis de supervivencia de otras ciencias es la presencia de datos censurados, la teoría aplica regresión de Cox para su modelamiento, en la presente investigación no se toma en cuenta datos censurados, como lo propone (Pereira et al. 2012), cuya variable dependiente es el tiempo de supervivencia o la tasa de riesgo, y asume que las empresas fracasadas y no fracasadas son de la misma muestra poblacional, considerando a las empresas no fracasadas como observaciones censuradas.
Una debilidad del análisis de cierre empresarial con la tabla de mortalidad es que este no toma en cuenta la posibilidad de no estacionariedad en los datos de cierre, explicado sobre todo por contracciones del ciclo económico; esta crítica fue fundamentada por Martin y Sunley (2015).
7. Conclusiones
Al analizar la estructura del tejido productivo ecuatoriano, las empresas de menor tamaño son las más numerosas, pero las empresas grandes concentran más ventas y empleo; la demografía empresarial refleja el estancamiento económico, ya que hay reducción del número de empresas activas. Las empresas de menor tamaño son más vulnerables; además del total de empresas creadas, apenas el 37,74 % continuaron activas al 2018, de estas, el 65,41 % eran sociedades anónimas y el 33,48 %, empresas de responsabilidad limitada.
La tasa de natalidad fue del 6,5 % anual y en los últimos años el promedio bajó a 4,1 %. En lo referente al cierre de empresas, el 60 % fueron microempresas y el 29 %, pequeñas, por lo que las empresas más pequeñas son más vulnerables al sistema. Las empresas antiguas permanecían por mucho más tiempo; sin embargo, en la actualidad, las que cierran tienen un promedio de vida de 3 años, mientras que hace 50 años tenían una probabilidad de vida de 32 años.
En el periodo 2016-2018, el número de empresas cerradas fue superior al de empresas creadas, lo que da como resultado tasas netas de crecimiento negativas en el número de empresas activas.
La probabilidad de que una empresa creada entre 2000 y 2018 siga en funcionamiento luego de tres años es del 83,26 %. Así, la probabilidad de que sobreviva por 6 años es del 60,82 %. La creación neta de empresas se encuentra directamente asociada a las tasas de crecimiento del sector económico; cuando este se contrae, las empresas tenderán a salir del mercado o a cesar actividades. La falta de apoyo financiero y de políticas gubernamentales restringen la sobrevivencia empresarial; de igual forma, el cierre puede estar asociado a la falta de rentabilidad y a los problemas de financiamiento.
En cuanto a los resultados de la tabla de mortalidad empresarial, se evidencia una fortaleza en relación con los modelos tradicionales como el logit y el análisis discriminante, ya que aportan información sobre la probabilidad de supervivencia o cierre empresarial de una empresa que ya está en funcionamiento x años; es decir, la probabilidad de supervivencia o cierre cambia en función de la edad que tiene la empresa. La tabla de mortalidad obtenida muestra la función de supervivencia S(x), que es la probabilidad de supervivencia a cualquier edad de una empresa recién creada; la función de distribución F(x), que nos indica la probabilidad de fallecimiento a cualquier edad de una empresa recién creada; la probabilidad anual de supervivencia de una empresa condicionada a que tiene la edad x (Px); y la probabilidad anual de fallecimiento condicionada a que la empresa ya tiene la edad x (qx).