Factores que determinan el rendimiento académico en Matemáticas en el contexto de una universidad tecnológica: aplicación de un modelo de ecuaciones estructurales^*

Determinants of academic performance in Mathematics in the context of a technological university: application of Structural Equations Model

Marcia Mercedes Vargas Hernández^**
Universidad Nacional de Ingeniería, Nicaragua

Eiliana Montero Rojas
Universidad de Costa Rica, Costa Rica

Notas
^*Artículo de investigación. La investigación tuvo un apoyo parcial de un organismo de Suecia, ASDI-SAREC, el resto contó con el apoyo de la Universidad Nacional de Ingeniería, Managua, Nicaragua.

Notas de autor

^**Correo electrónico: marcia.vargas@fiq.uni.edu.ni; eiliana.montero@ucr.ar.creiliana

Recepción: 19 Febrero 2014 Aprobación: 22 Septiembre 2016

Para citar este artículo:

Vargas, M.M. & Montero, E. (2016). Factores que determinan el rendimiento académico en Matemáticas en el contexto de una universidad tecnológica: aplicación de un Modelo de Ecuaciones Estructurales. Universitas Psychologica, 15 (4). http://dx.doi.org/10.11144/Javeriana.upsy15-4.fdra

Resumen

El estudio examinó, por medio de un modelo de ecuaciones estructurales, posibles factores causales del rendimiento académico en cursos de Matemáticas de la Universidad Nacional de Ingeniería de Nicaragua, en una muestra estratificada por conglomerados de 713 estudiantes de segundo año distribuidos en 33 grupos de clases, con sus respectivos profesores. Además de la nota final en el curso, se incluyeron en el modelo causal, y de acuerdo con la literatura, variables de dimensiones sociodemográficas, psicosociales, institucionales y pedagógicas. Los resultados destacan tres variables del estudiante como determinantes del desempeño en el curso de Matemática: la inteligencia fluida, los hábitos de estudio y las actitudes negativas hacia las Matemáticas, resultando relevantes también los efectos indirectos en las dos primeras, y en las direcciones esperadas. Las variables del docente que mostraron efectos directos de importancia fueron edad, nivel académico y la asistencia a cursos pedagógicos promovidos por la institución.

Palabras clave : educación superior, modelos de ecuaciones estructurales, predicción, rendimiento en matemática.

Abstract

The study examined, using structural equations model (SEM) possible causal factors for Math achievement in students from the National University of Engineering in Nicaragua, using a stratified sample of complete conglomerates of 713 students in second year, spread over 33 groups and their respective teachers. Besides the final grade in the course, and according to the literature review, variables of the socio-demographic, psychosocial, institutional and pedagogical dimensions were included in the model. The results emphasized three student variables as determinants of the achievement in Math: fluid intelligence, study habits and negative attitudes towards Mathematics, with the indirect effects of the last two also relevant, and in the expected direction. Teacher variables that showed relevant direct effects were age, academic level and attendance to pedagogical courses promoted by the institution.

Keywords: Higher education, Math achievement, prediction, Structural Equations Model.

Introducción

La Universidad Nacional de Ingeniería (UNI) de Nicaragua es una institución pública dedicada a formar profesionales en el campo de la Ingeniería y la Arquitectura, con una población estudiantil de 10.880 (Programa Institucional de Evaluación y Acreditación Universitaria, PIEAU-UNI, 2010), capta al menos el 50% de la demanda nacional; sus estudiantes presentan bajo rendimiento académico, particularmente en los cursos básicos de Matemáticas, Física y Estadística. Por lo tanto, valorar esta problemática es trascendental, máxime aún, por el papel que juegan estas disciplinas en esta formación profesional (PIEAU-UNI, 2004)

Esta investigación tiene como propósito examinar, desde un planteamiento de relaciones de causalidad, un conjunto de factores, de diversa naturaleza, individuales y contextuales del estudiantado, que pueden ser tipificados desde cuatro grandes dimensiones: Psicosocial, Pedagógica, Institucional y Sociodemográfica (Montero et al., 2007), y que se cree que pueden estar incidiendo en el rendimiento académico en Matemáticas.

A nivel mundial, el rendimiento académico en la disciplina de matemáticas ha sido históricamente bajo, en todos los niveles del sistema educativo, en consecuencia ha sido objeto de investigación e intervención permanente, existiendo actualmente esfuerzos mundiales como el Programa para la Evaluación Internacional de los (las) estudiantes (PISA), cuyo objetivo es evaluar hasta qué punto los alumnos cercanos al final de la educación obligatoria, en los países desarrollados, han adquirido algunos conocimientos y habilidades necesarias para la participación plena en la sociedad. También, existen numerosas investigaciones que abordan esta problemática en estudiantes universitarios en donde se identifican un conjunto de dimensiones inherentes a la personalidad del estudiante y su entorno, a las características y preparación académica del docente (García, Azcárate, & Moreno, 2006) y a la naturaleza de la Universidad (Cervini, 2003; Montero, Villalobos, & Valverde, 2007; Soria & Martínez, 2005; Rodríguez, 2007; Tejedor, 2003). Este estudio pretende generar evidencias para conocer mejor esta problemática utilizando datos de una universidad tecnológica: la Universidad Nacional de Ingeniería, de Nicaragua.

Esta investigación tiene como propósito examinar, desde un planteamiento de relaciones de causalidad, un conjunto de factores, de diversa naturaleza, individuales y contextuales del estudiantado, que pueden ser tipificados desde cuatro grandes dimensiones: Psicosocial, Pedagógica, Institucional y Sociodemográfica (Montero et al., 2007), y que se cree que pueden estar incidiendo en el rendimiento académico en Matemáticas.

Referentes teóricos

Actualmente, muchas investigaciones respaldan que las causales de la problemática del rendimiento académico están concentradas principalmente en el estudiantado, en sus características individuales, en su comportamiento, específicamente en factores psicosociales tales como: la motivación, las capacidades, tanto las innatas como las adquiridas, el autoestima. Hay posiciones teóricas que enfatizan la importancia de atender no solo los componentes cognitivos sino también los componentes afectivos y motivacionales. Es decir, se reconoce la existencia de interrelaciones durante el proceso enseñanza-aprendizaje que involucran variables motivacionales, afectivas, cognitivas y el rendimiento académico. (Alonso-Tapia, 1995; García & Pintrich, 1996; González-Pienda et al., 2003; Rinaudo, Chiecher, & Donolo, 2003; Schiefele, 1991; Wolters & Pintrich, 1998). Lo que no se sabe con rigurosidad es cómo interactúan los aspectos motivacionales, afectivos y cognitivos. Existe un debate particular, desde una perspectiva más amplia sobre el constructo "inteligencia" o habilidad intelectual y sobre las relaciones entre aptitudes, medidas por medio de pruebas de Inteligencia fluida —capacidades básicas de razonamiento— y la inteligencia emocional (De la Peza Casares & García, 2005; Gagné & Pérez, 2002), la Inteligencia fluida está menos influenciada por las oportunidades educativas previas y por la cultura, por estas razones es menos susceptible de ser modificada con intervenciones educativas (De Juan-Espinosa, 1997).

A su vez, se registran investigaciones centradas en examinar factores asociados a la calidad de la docencia como: la experiencia docente, el nivel académico, los estilos de enseñanza, la interacción profesor(a)-alumno(a), la capacidad de comunicación, las instrucciones metodológicas que se le dan al estudiante (Green, 1990). Algunos autores consideran que el rendimiento académico mejora cuando el profesorado es accesible y muestra interés o entusiasmo en la enseñanza, evidenciado en los tiempos y formas de atención; si facilita explicaciones o aclaraciones, más cuando sus estudiantes son personas jóvenes adultas y las conciben integralmente como personas (Latiesa, 1992; Page et al., 1990).

Sobre este aspecto, investigadores de la educación matemática se han centrado en la enseñanza, examinando cuál es la relación existente entre la comprensión del contenido de la disciplina y su conocimiento de diferentes sistemas de representación y abstracción, (Azcárate, 1997; Blanco, 1997; Llinares, 1996, 2000). Asimismo, Azcárate (1997) define una posición sobre los saberes del docente de Matemáticas enfatizando un conocimiento profesional integrado más allá del conocimiento disciplinar, rasgo que ha caracterizado al docente tradicional desde una reproducción conductista, mecanicista del contenido disciplinar.

Otras investigaciones arguyen que la problemática reside en las características de las instituciones educativas y los insumos educacionales, los recursos financieros, disponibilidad de literatura, calidad organizativa de la facultad, el diseño curricular y los métodos de enseñanza que promueven, (Latiesa, 1992). Aquí, se sitúa la tercera dimensión que comprende los factores institucionales tales como los horarios de clases, los tamaños de los grupos, la cantidad de libros disponibles en la biblioteca, el ambiente institucional desde la perspectiva de la infraestructura y los aspectos relacionados con la carrera que cursa el estudiantado.

Desde los factores sociodemográficos se plantea que el comportamiento humano y el desarrollo de la personalidad están altamente influenciados por factores sociales y culturales, enfatizándose la influencia de las relaciones y características de los padres sobre los hijos (Le Compte & Preissle 1993). Hay investigaciones que argumentan que la problemática reside en factores de carácter individual, social y cultural del estudiantado, o sea, en variables sociodemográficas tales como el sexo, el nivel económico de la familia, el tipo de institución educativa donde realizó sus estudios de secundaria, (urbana o rural, pública o privada), el nivel educativo de los padres, entre otros (Montero et al., 2007). En Nicaragua, los centros educativos urbanos y privados presentan mejores condiciones de infraestructura y calidad académica de los docentes que los rurales y los públicos, (Arcia, Porta, & Laguna, 2004).

Se ha demostrado la relación directa entre el nivel socio económico y el rendimiento académico, los grupos más pobres suelen tener más problemas para desarrollar sus habilidades intelectuales, en consecuencia presentan un bajo desempeño académico, (Rivero, 2000). Asimismo, el nivel académico de los padres (Bandura, 1982) y el apoyo familiar tienen una incidencia directa en el rendimiento académico (González-Pienda et al., 2003).

En cuanto a si el sexo influye o no en el desempeño académico en Matemáticas, hay posiciones encontradas, unas patentizan que los hombres tienen un mejor rendimiento que las mujeres, (Ruiz De Miguel & Castro, 2006), otras, la posición contraria (Stage & Kloosterman, 1995) y una tercera posición asevera que es indiferente del sexo (Mittelberg & Lilach, 1999), son otros elementos ambientales, personales, socioculturales, de socialización, (Fennema & Peterson, 1985), las relaciones con el profesorado, la autoconfianza, la motivación (Page et al., 1990) los que influyen en el rendimiento académico.

Indicadores del Rendimiento Académico

Obtener una medida objetiva de este constructo es complejo y en muchos casos hasta controversial, debido a todas las variables y formas de cálculo a considerar en dependencia de la naturaleza de los contenidos de la materia a evaluar y del docente. Históricamente, es ampliamente aceptado que las notas de un examen como producto de una evaluación de un curso en un período de tiempo establecido, constituyen los indicadores más comunes de un determinado aprendizaje, siendo este un criterio social, legalmente aceptado en el sistema educativo (Page et al., 1990; Rodríguez, Fita, & Torrado, 2004; Tournon, 1984).

Además, se considera un indicador preciso para valorar el rendimiento académico, asumiendo que reflejan los logros académicos en los diferentes componentes del aprendizaje. No obstante, poseen un valor relativo de la medida del rendimiento debido a que de cierta forma dependen de la naturaleza de los cursos del profesorado, del centro educativo y hasta del nivel dentro del sistema educativo (Montero et al., 2007). Gran parte de las investigaciones toman dos tipos de medidas: las pruebas objetivas estandarizadas y las calificaciones del profesorado que, como demuestran Marreno y Espino (1988) son entre sí medidas complementarias. En esta investigación, el indicador valorado es la nota de final de curso de Matemáticas III de un total de cuatro cursos obligatorios.

Método

Participantes

713 estudiantes de segundo año de carrera en la Universidad Nacional de Ingeniería, Managua, Nicaragua, en el año 2010, distribuidos en 33 grupos de clases con sus respectivos profesores en el curso de Matemáticas III. Fueron seleccionados usando un muestreo aleatorio estratificado por conglomerados completos, siendo los grupos los conglomerados y las carreras los estratos.

Instrumentos

Con base en los resultados de la fase exploratoria, las hipótesis establecidas, la delimitación de las dimensiones, constructos y variables involucradas, fueron diseñados dos cuestionarios: uno para el estudiantado y otro para el profesorado. En este diseño fueron considerados los instrumentos de Montero, Villalobos y Cubero (2004); el de Evaluación Docente, de la Universidad de Costa Rica (UCR); la Escala de motivación con base en metas académicas en contextos universitarios de Hayamizu y Weiner (1991); parte del Inventario de Actitud hacia las Matemáticas, versión en Español de Fennema y Sherman (1976), la Escala de rasgos de personalidad Big Five versión reducida en español de Costa & McCrae, (1992); la Escala de autoeficacia de Baessler & Schwarzer (1996); la de Inteligencia Emocional de Montero et al. (2007); Hábitos de estudio de Barragán (2008). También fueron incluidos algunos ítems para conocer las condiciones socioeconómicas de los estudiantes nicaragüenses. Adicionalmente, al estudiantado se le aplicó el Test de Cattell, escala 3, forma A (R. B. Cattelle, & A. K. Cattelle, 2001).

Procedimiento

Fase Exploratoria . Primeramente, se valoró la percepción de una muestra de profesores y estudiantes acerca de la problemática del rendimiento académico y sus factores incidentes. Se utilizó la técnica de la selección de estrategias de casos, escogidos al azar, (Valles, 2000), con base en criterios técnicos pre-establecidos según los referentes teóricos consultados y el conocimiento del contexto particular de la investigadora. Se seleccionaron profesores de Matemáticas, con más de 5 años de experiencia en docencia universitaria. Por otra parte, se seleccionaron estudiantes tanto de alto como de bajo rendimiento, con matrícula activa, con cursos obligatorios de Matemáticas aprobados. Estos resultados fueron parte de los insumos para el diseño y validación posterior de los cuestionarios.

Fase de Desarrollo . Validación previa de los cuestionarios. Tres técnicas fueron empleadas: juicio de expertos, aplicación del instrumento uno a uno con entrevista semi-estructurada posterior y la prueba piloto la cual fue realizada a 149 estudiantes de seis (6) grupos de clases aleatorios y a los profesores de Matemáticas de esos grupos. Se efectuaron los análisis psicométricos respectivos con Teoría Clásica de los Test, de los constructos representados en las escalas utilizadas, un valor de alfa de Cronbach (α) ≥ 0.70 fue considerado satisfactorio.

Fase final: análisis y modelación . Un modelo de Ecuaciones Estructurales o SEM por sus siglas en inglés, es un método de análisis multivariado que combina aspectos del análisis de regresión múltiple y el análisis factorial para tratar de analizar relaciones de dependencia complejas, propias de fenómenos sociales, donde interactúan variables latentes (Bollen, 2002) y variables manifiestas, permite valorar sus efectos causales en investigaciones no experimentales y de relaciones lineales (Cheung & Kevin, 2005; Goldstein, 1987). Esta causalidad es estadística y no filosófica siendo un modelo confirmatorio guiado por la teoría (González, 2003).

El elevado número de variables predictoras hizo técnicamente imposible la estimación de un modelo de ecuaciones estructurales (SEM) que las incluyera todas conjuntamente. Fue necesario entonces realizar una depuración o limpieza inicial para retener un menor número de variables que fueran las candidatas para la modelación estructural.

Esta depuración se realizó tanto desde la teoría, eliminando aquellas para las cuales hubiera menos consenso o solidez en cuanto a su influencia causal sobre el desempeño en Matemática y también desde la evidencia estadística correlacional que presentaban los datos. Después de este proceso, un total de 13 variables fueron las que finalmente se incluyeron en el modelo estructural. Igualmente por razones de estimación, solamente fue posible ajustar un SEM de Análisis de Trayectoria o de Senderos.

Las variables que se consideraron inicialmente pero que por razones teóricas o estadísticas no se incluyeron finalmente en el modelo estructural son las siguientes:

Variables del estudiante: sexo, edad, lugar de origen, condición laboral, nivel académico de los padres, opción inicial de carrera, escala de motivación de acuerdo a metas de aprendizaje, escala de metas de refuerzo social, escala de metas de logro, escala de inteligencia emocional, percepción del desempeño académico del (la) docente por parte del estudiantado, valoración del estudiantado de la asistencia del (la) docente de Matemáticas III a clases, horario de estudio (nocturno o diurno), tipo de colegio de procedencia (privado, estatal o subvencionado, rasgos de personalidad: conciencia, neuroticismo y apertura, escala socioeconómica, satisfacción con aspectos institucionales de planeación académica, con infraestructura, servicios estudiantiles, escala de apoyo afectivo de padres, otros familiares, amigos, compañeros de la universidad y profesores, percepción del estudiantado sobre la actitud de los padres con las Matemáticas, escala de Matemáticas con un dominio masculino y autoeficacia.

Variables predictoras del docente y del curso: tipo de contratación del profesorado, trabajo extraordinario fuera de la Universidad, percepción de la asistencia del estudiantado a clases, percepción del profesorado de Matemáticas III sobre el interés que tiene el estudiantado en la asignatura, percepción del profesorado de Matemáticas III sobre la responsabilidad que tienen los (las) estudiantes en la asignatura que les imparte, grado de interés en el curso, grado de satisfacción con el curso.

La descripción de las 13 variables que formaron parte del modelo estructural es la siguiente:

Variables del estudiante

Variable dependiente: El rendimiento académico final en el curso de Matemáticas III, Mate3PROM. Es la nota final del Curso de Matemáticas III, escala de 0 a 100 puntos, 60 nota de aprobación.

PromSEC: Promedio de Secundaria, notas de cuarto y quinto año de bachillerato. Escala de 0 a 100 puntos.

IFluida: Inteligencia fluida. Test de Cattell. (α) = 0.78. Test-Retest.

HabitosEstudio: Hábitos de estudio. Escala compuesta por 12 ítems, rango de calificación de 5 a 60 puntos, cada ítem fue valorado en una escala de 1 a 5 puntos, 1 = lo más bajo y 5 = lo más alto . Valores altos denotan altos hábitos de estudio, α = 0.79.

ActNegativaMate: Actitud negativa hacia las Matemáticas. Escala compuesta por ocho ítems, mide la falta de confianza del (la) estudiante en su propia capacidad para hacer lo mejor en Matemáticas y la ausencia de control percibido sobre las causas que provocan malos resultados. Rango de calificación de 8 a 40 puntos, cada ítem se calificó con una escala Likert de 1 a 5, donde 1 es lo más bajo y 5 la más alto, α = 0.88. Variables del profesorado y el curso

Variables del profesorado y el curso

EdadProf: Edad del (la) profesor(a), en años cumplidos.

Posgrado: Nivel académico del profesorado. 1 = representa a los (las) que tiene posgrado y 0 = los (las) que tienen Licenciatura y egresados .

NumeroEstGrupo: Cantidad exacta de estudiantes por grupo de clases.

PerAutoEficaciaP: Estabilidad emocional del (la) profesor(a). Considerada como un índice, es la sumatoria de 14 aspectos, escala tipo Likert de 1 a 5, rango de 14 a 70 puntos.

TEnsPrMa: Técnicas de enseñanza comparativa entre las técnicas con enfoque participativo y las técnicas con enfoque conductual: valor 1 = las técnicas participativas son igual o mayor de 50% y 0 = en los demás casos .

GradoSTrabajop: como un índice, es la sumatoria de ocho aspectos relacionados con las condiciones de trabajo, escala tipo Likert de 1 a 5, rango de 8 a 40 puntos.

AsisCursoPedag: Asistencia a cursos pedagógicos obligatorios, escala tipo Likert, 1 = nunca y 5 = siempre .

MedidasRemp: Si el profesorado aplica medidas remediales cuando los (las) estudiantes reprueban. 1 = si lo realiza . 0 = no lo realiza .

Resultados

Identificación del modelo causal

El modelo propuesto cuenta con p = 10 variables exógenas observadas y q = 3 variables endógenas. Las relaciones causales entre las variables exógenas observadas y endógenas intermedias y final están representadas por los coeficientes gamma (γ) y las relaciones causales entre variables endógenas están representadas por los coeficientes beta ( β ). Existen un total de 13 variables con 14 relaciones causales (gamma ó beta, según sea el caso). Con esta cantidad de variables (según la regla t , p =10 y q = 3) y la cantidad de parámetros libres a estimar, coeficientes gamma (γ) y beta ( β ), el modelo causal está bien identificado, es decir, es factible determinar su solución, según la regla T citada en Cea D'Ancona (2002).

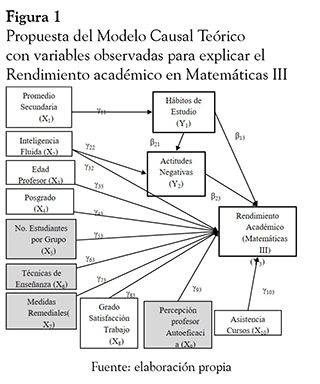
De los resultados del modelo causal estimado, en el estudiantado se determinó que las variables Inteligencia fluida, Hábitos de estudio y Actitudes negativas hacia la Matemáticas tienen un efecto causal directo sobre el Rendimiento Académico, el de las dos primeras es positivo en cambio el de la última es negativo, resultados que son consistentes con los planteados en los referentes teóricos. Las dos primeras, Inteligencia fluida y Hábitos de estudio, además de tener un efecto causal con el rendimiento académico en Matemáticas, también ejercen un efecto causal sobre Actitudes negativas hacia las Matemáticas. Esto implica que el comportamiento de las Actitudes negativas hacia las Matemáticas está influido por los Hábitos de estudio y por la Inteligencia fluida. Por otra parte, la relación de causalidad entre el Promedio de Secundaria y los Hábitos de estudio debe interpretarse así: al no existir un indicador de los hábitos de estudios en secundaria el promedio de rendimiento obtenido en este nivel es un proxy para los hábitos de estudios en la Universidad que se midieron en esta indagación. Esto nos da evidencias acerca de la pertinencia y relevancia de visionar el análisis de este conjunto de variables de forma sistémica de tal manera que se puedan proponer intervenciones en variables que son fundamentales para el mejoramiento del Rendimiento Académico, tal es el caso de las Actitudes negativas hacia las Matemáticas y de los Hábitos de estudio, sin embargo hay que considerar la importancia predictora de la Inteligencia fluida en el sentido que representa un insumo de base fundamental en cualquier intervención educativa, que no es fácilmente modificable y debe medirse en la población meta. El Promedio de Secundaria, contrario a lo esperado, no presentó una relación causal directa con el Rendimiento Académico quizás este resultado se debe a que se trata de un constructo de diferente naturaleza.

Las variables del profesorado y el curso, que resultaron relevantes para predecir el Rendimiento fueron: Edad, Nivel Académico, la Asistencia a cursos pedagógicos promovidos por la institución, Grado de satisfacción en el trabajo, todas ellas resultaron en la dirección esperada. En el caso de la edad, se esperaba que la relación fuera inversa, los estudiantes de los profesores más jóvenes fueron los que obtuvieron los mejores rendimientos académicos, controlando las demás variables en el modelo, situación que podría explicarse por mayor similitud en sus contextos personales y pedagógicos.

Aunque la prueba Chi-cuadrado de bondad de ajuste rechazó la hipótesis nula de igualdad de las matrices de covariancias observada y estimada según el modelo, los otros índices de bondad de ajuste evaluados fueron satisfactorios, el error de la raíz cuadrada de la media de aproximación (RMSEA = 0 < 0.05), el índice de la raíz cuadrada media residual (RMR = 0.031 < 0.05), el índice de ajuste normalizado (NFI = 0.97 > 0.95), el índice de bondad de ajuste (GFI > 0.95), el índice de bondad de ajuste ajustado (AGFI = 0.99 > 0.95) y el índice de bondad de ajuste de parsimonia (PGFI = 0.70). Es relevante indicar que el resultado de Chi-cuadrado puede ser debido, en parte, al efecto del elevado tamaño de muestra.

Es necesario valorar la importancia de que el profesorado esté consciente que, dentro de su rol docente, la implementación de estrategias pedagógicas y didácticas orientadas a fomentar actitudes positivas en los (las) estudiantes hacia las Matemáticas y a su vez desarrollar actividades sistemáticas que ayuden a fortalecer los hábitos de estudio, en la medida que el profesorado incida positivamente en estos dos aspectos se estiman mejoras sustantivas en el rendimiento académico en Matemáticas.

Además, parece ser ineludible determinar objetivamente el nivel de las habilidades que posee el estudiantado —inteligencia fluida— así como también, conocer las actitudes que tiene hacia el aprendizaje de las Matemáticas puede constituirse en una información muy valiosa para el profesorado durante el proceso de instrucción. A su vez, esta información podría ser una herramienta clave para el estudiantado porque al estar consciente de sus habilidades —Inteligencia fluida— estaría en mejor capacidad de tomar decisiones vocacionales más apropiadas. De igual manera, el estudiantado podría emprender un conjunto de iniciativas —actividades, tareas— para fortalecer y mejorar sus hábitos de estudio.

El profesorado debe estar consciente del doble desafío que enfrenta en su práctica educativa, el primero consiste en enseñar apropiadamente los conocimientos y destrezas relevantes de la disciplina y el segundo deberá estar orientado a fortalecer la interacción y por ende, las relaciones profesor(a)-estudiante que permitan fomentar mayores y mejores hábitos de estudios, motivar y fomentar actitudes positivas hacia el aprendizaje de las Matemáticas.

Es fundamental destacar que, por una parte, para la Psicología, especialmente para la Psicología Educativa, algunos de estos hallazgos presentan gran relevancia. El hecho de que el indicador de inteligencia fluida haya resultado importante como predictor, tanto a nivel directo como indirecto, por medio de las actitudes negativas, nos hace nuevamente reflexionar en torno a la permanente discusión de "naturaleza versus crianza", en cuanto a factores externos e internos al individuo que moldean y explican su comportamiento observado. Estos resultados estarían explicados por las complejas dinámicas que se producen en el individuo y que son responsables del desarrollo de sus diversas capacidades intelectuales y rasgos afectivos. Para las actitudes negativas, en este caso particular, se podría conjeturar que la relación encontrada da cuenta de mecanismos asociados al aprendizaje social, de reforzamientos negativos durante la historia académica del estudiante, al vivir experiencias poco motivadoras con la Matemáticas en la primaria y secundaria. Es una posible explicación para esa actitud más desfavorable en las personas con niveles relativamente más bajos de inteligencia fluida.

Aun así, los resultados también sugieren que se podría mejorar el desempeño en Matemáticas interviniendo en las actitudes negativas; el indicador de este constructo se refiere a la falta de confianza del (la) estudiante en su propia capacidad para hacer lo mejor en Matemáticas y a la ausencia de control percibido sobre las causas que provocan malos resultados. Entonces, entre más externo sea el estilo atribucional de la persona en cuanto a factores que influyen en su desempeño, menor tenderá a ser su rendimiento en Matemáticas.

Y, por otra parte, este estudio también confirma la relevancia de definir conceptualmente diversas dimensiones de autoeficacia, según ámbitos específicos de tareas o conductas, en este caso particular referidas a la confianza percibida en su propia capacidad para "hacerlo bien en matemáticas". Los resultados del estudio se podrían conjeturar como posiblemente generalizables a contextos de carreras de Ingeniería en universidades públicas de América Latina, en donde existe gran desigualdad en las oportunidades educativas previas de los estudiantes causada por razones diversas propias del estudiante, de su contexto, de la formación recibida (colegio y profesorado), de su orientación vocacional, entre otros.

Referencias

Alonso-Tapia, J. (1995). Motivación y aprendizaje en el aula. Cómo enseñar a pensar . Madrid: Santillana.         [ Links ]

Arcia, R., Porta, E., & Laguna, J.R., (2004). Análisis de factores asociados al rendimiento académico en 3º y 6º grado de primaria. Nicaragua: PREAL, UNICEF, CARE y Ministerio de Educación Cultura y Deportes (MECD). Recuperado de http://www.mined.gob.ni/pdf2005/pdf2004/Factores%20Asociados%20Nicaragua%202004.pdf         [ Links ]

Azcárate, P. (1997). Sobre el conocimiento didáctico del contenido: dilemas y alternativa. En M. Sierra, & L. Rico (Eds.), Primer Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 25-33). Zamora: Universidad de Granada.         [ Links ]

Baessler, J. y Schwarzer, R. (1996). Evaluación de la Autoeficacia: Adaptación española de la escala de Autoeficacia General. Ansiedad y Estrés , 2 , 1-8.         [ Links ]

Bandura, A. (1982). Self-efficacy mechanism in human agency. American Psychologist , 37 (2), 122-147.         [ Links ]

Barragán, C. (2008). Factores asociados al rendimiento académico de los estudiantes de educación superior utilizando un modelo multinivel: el caso de la Universidad Autónoma de Guerrero, México . (Tesis de maestría). Recuperado de http://www1.sep.ucr.ac.cr/administrator/archivos/pdf/Doct_Educacion/Tesis_Doct_Educ.2.pdf         [ Links ]

Blanco, L., (1997). Tipos de tareas para desarrollar el conocimiento didáctico del contenido. En M. Sierra, & L. Rico (Eds.), Primer Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 34-40). Zamora: Universidad de Granada.         [ Links ]

Bollen, K., (2002). Latent Variables Psychology and the social sciences. Annual Review of Psychology , 53 , 605-634.         [ Links ]

Cattell, R. B., & Cattell, A. K. S. (2001). Test de Factor g. Escala 3A . Madrid: TEA Ediciones. S. A.         [ Links ]

Cea D 'Ancona, M.A. (2002). Análisis Multivariable. Teoría y Práctica en la Investigación Social . España: Editorial Síntesis.         [ Links ]

Cervini, R. (2003). Relaciones entre la composición estudiantil, proceso escolar y el logro de las Matemáticas en la educación secundaria en Argentina. Un modelo de tres niveles. Revista Electrónica de Investigación Educativa , 5 (1), 72-98.         [ Links ]

Cheung, M., & Au, K. (2005). Applications of Multilevel Structural Equation Modeling to Cross-Cultural Research. Structural Equation Modeling , 12 (4), 598-619.         [ Links ]

Costa, P.T., & McCrae, R. (1992). NEO PI-R Personality Inventory. Spanish Big Five Inventory Manual . Odessa, FL: Psychological Assessment Resources.         [ Links ]

De Juan-Espinosa, M. (1997). Geografía de la inteligencia humana. Las aptitudes cognitivas . España: Ediciones Pirámide S. A.         [ Links ]

De la Peza Casares, R., & García, E. (2005). Relación entre variables cognitivo-emocionales y rendimiento académico: Un estudio con universitarios. Iberpsicología , 10 (7).         [ Links ]

Fennema, E., & Sherman, J.A (1976). Fennema-Sherman Mathematics Attitudes Scales: Instruments designed to measure attitudes toward the learning of Mathematics by females and males. Journal for Research in Mathematics Education , 7 , 324-326.         [ Links ]

Fennema, E., & Peterson, P., (1985). Autonomous learning behavior: A possible explanation of gender-related differences in mathematics. In L.C. Wilkinson & C.B. Marret (Eds.), Gender-related differences in classroom interactions (pp. 17-35), New York: Academic Press.         [ Links ]

Gagné, F., & Pérez, F., (2002). ¿When IQ is controlled, does motivation still predict achievement? Intelligence , 30 (1), 71-100.         [ Links ]

García, T., & Pintrich, P. (1996). The effects of autonomy on motivation and performance in the college classroom. Contemporany Educational Psychology , 21 , 447-486.         [ Links ]

García, L., Azcarate, C., Moreno, M. (2006). Creencias, concepciones y conocimiento profesional de profesores que enseñan cálculo diferencial a estudiantes de ciencias económicas. Revista Latinoamericana de Investigaciones en Matemática Educativa. RELIME , 9 , 85-116.         [ Links ]

Global University Network for innovation. GUNI (2009). La Educación Superior en tiempos de cambio. Nuevas dinámicas para la responsabilidad Social . Madrid-Barcelona-México: Ediciones Mundi-Prensa.         [ Links ]

Goldstein, H. (1987). Multilevel models in educational and social research. London. Griffin; New York: Oxford University press.         [ Links ]

González, L. D. (2003). Modelamiento Estructural en las Ciencias Sociales . México: Editorial Unison Rosales y Blvd. Luis Encinas.         [ Links ]

González-Pienda. J., Núñez J., Álvarez L., Roces C., González-Pumariega S., González P.,Bernardo A. (2003). Adaptabilidad y cohesión familiar, implicación parental en conductas autoregulatorias, autoconcepto del estudiantes y rendimiento académico. Psicothema , 15 (3), 471-477. Recuperado de http://www.psicothema.com/pdf/1090.pdf.         [ Links ]

Hayamizu, T., & Weiner, B. (1991). A test Dweck´s model of achievement goals as related to perceptions of ability. Journal of Experimental Education , 59 , 904-915.         [ Links ]

Latiesa, M. (1992). La deserción universitaria, desarrollo de la escolaridad en la enseñanza superior. Éxitos y fracasos . España: Siglo XXI de España Editores S.A.         [ Links ]

Green, L.E.T. (1990). Test anxiety, Mathematics Anxiety, and Teacher Comments relationships to achievement in remedial Mathematics Classes. Journal of Negro Education , 59 (3). 320-335. http://dx.doi.org/10.2307/2295567         [ Links ]

Llinares, S. (1996). Conocimiento profesional del profesor de matemáticas: conocimiento, creencias y contexto en relación a la noción de función. En J.P. Ponte, C. Monteiro, M. Maia, L. Serrazina, & C. Loureiro (Coords.), Desenvolvimento Professional dos Professores de matemática. Que Formaçao? (pp. 47-82). Sociedade Portuguesa de Ciencias da Educaçao, Secçao de Educaçao Matemática: Lisboa.         [ Links ]

Llinares, S. (2000) Intentando comprender la práctica del profesor de matemáticas. En J. Ponte & L. Serraniza (Coords.), Educaçao Matemática em Portugal, Espanha e Italia . (pp. 109-132). Secçao de Educaçao Matemática da Sociedade Portuguesa de Ciêncas de Educaçao: Lisboa, Portugal.         [ Links ]

Marreno, H., & Espino, O. (1988). Evaluación comparativa del poder predictor de las aptitudes sobre las notas escolares y pruebas objetivas. Revista de Educación , 287 , 97-112.         [ Links ]

Mittelberg, D., & Lilach L., (1999). Confidence in mathematics and its consequences: gender differences among Israelí Tewish and Arab Jouth. Gender and Education 11 (1), 75-92. http://dx.doi.org/10.1080/09540259920771         [ Links ]

Montero, E., & Villalobos, J. (2004). Factores institucionales, pedagógicos, psicosociales y sociodemográficos asociados al rendimiento académico en la UCR . (Informe final). Costa Rica: Universidad de Costa Rica.         [ Links ]

Montero, E., Villalobos, J., & Cubero, R. (2004). Cuestionario para Estudiantes. Instituto de Investigaciones Psicológicas . Universidad de Costa Rica (UCR).         [ Links ]

Montero, E., Villalobos J., & Valverde B. (2007). Factores institucionales, pedagógicos, psicosociales y sociodemográficos asociados al rendimiento académico en la Universidad de Costa Rica: Un análisis multinivel. Relieve, 13 (2), 215-234. Recuperado de http://www.uv.es/relieve/v13n2/RELIEVEv13n2_5.htm         [ Links ]

Page, M., Bueno, M.J., Callejas, J.A, Cerdán, J., Echeverría, M.J., García, C., Trillo, C. (1990). Hacia un modelo causal del rendimiento académico . Madrid: Centro de Publicaciones del Ministerio de Educación y Ciencia (CIDE). Recuperado de https://dialnet.unirioja.es/servlet/libro?codigo=378869         [ Links ]

Programa Institucional de Evaluación y Acreditación Universitaria. PIEAU-UNI (2004). Informe de Autoevaluación Institucional . Managua, Nicaragua: Universidad Nacional de Ingeniería (UNI).         [ Links ]

Programa Institucional de Evaluación y Acreditación Universitaria. PIEAU-UNI (2010). Informe de Autoevaluación Institucional . Managua, Nicaragua: Universidad Nacional de Ingeniería (UNI).         [ Links ]

Rinaudo, M.C., Chiecher A., & Donolo, D. (2003). Motivación y uso de estrategias en estudiantes universitarios. Su evaluación a partir del Motivated Strategies Learning Questionnaire. Anales de psicología , 19 (1), 107-119.         [ Links ]

Rivero, J. (2000). Reforma y desigualdad educativa en América Latina. Revista Iberoamericana de educación , 23 . Recuperado de http://rieoei.org/rie23a03.htm         [ Links ]

Rodríguez, M. N. (2007). Análisis Multivariado del desempeño académico de los estudiantes universitarios de Química . Tesis de Doctorado. Universidad Autónoma de Madrid, España.         [ Links ]

Rodríguez, S., Fita S., & Torrado, M. (2004). El rendimiento académico en la transición secundaria-universidad. Revista de Educación , 334 , 391-414. Recuperado de http://www.revistaeducacion.educacion.es/re334/re334_22.pdf         [ Links ]

Ruiz De Miguel, C., & Castro, M., (2006). Un estudio multinivel basado en PISA 2003: Factores de eficacia escolar en el área de Matemáticas. Educativas. Archivos Analíticos de Políticas Educativas , 14 (29), 1-26. Recuperado de http://epaa.asu.edu/ojs/article/viewFile/100/226        [ Links ]

Schiefele, U. (1991). Interest, learning and motivation. Educational Psychology , 26 (4), 299-323.         [ Links ]

Stage, F., & Kloosterman, P. (1995). Gender, Beliefs and Achievement in remedial collage level mathematics. The Journal of Higher Education , 66 (3), 294-311.         [ Links ]

Tejedor, J. (2003). Poder Explicativo de algunos determinantes del rendimiento en los estudios universitarios. Revista Española de Pedagogía, LXI (224), 5-32.         [ Links ]

Tournon, J., (1984). Factores del rendimiento académico en la universidad . España: Ediciones Universidad de Navarra, S.A. (EUNSA).         [ Links ]

Valles, M. (2000). Técnicas cualitativas de investigación social. Reflexión metodológica y práctica profesional . Madrid, España: Editorial Síntesis S.A.         [ Links ]

Wolters, C., & Pintrich, P. (1998). Contextual differences in student motivation and self-regulated learning in mathematics, English and social studies classrooms. Instructional Science , 26 (1-2), 27-47.         [ Links ]