Introducción
Los avances de los recursos tecnológicos para la enseñanza de las matemáticas y las exigencias por parte de entes educativos ministeriales de los países con respecto a que el profesorado utilice las TIC como herramientas de su quehacer y planificación pedagógica en el día a día, denotan la relevancia que hoy tiene que un profesor que enseña matemática tenga conocimiento de herramientas tecnológicas plasmadas de manera efectiva en su práctica (Montoya y González, 2019). Por lo que la capacitación a profesores desarrolladas por centros educativos, directivas y políticas de estado y el acceso a herramientas TIC son elementos necesarios para mejorar la calidad y eficacia de la educación (Cabero y Valencia, 2019; Padilla-Escorcia y Conde-Carmona, 2020; Conde-Carmona y Padilla-Escorcia, 2021; Conde-Carmona, Fontalvo-Meléndez y Padilla-Escorcia, 2021). Ya que de acuerdo con Schõn (1987), es importante que los profesores renueven sus métodos de enseñanza a partir de los resultados que obtienen en sus prácticas diarias. Por lo que la interacción con las TIC es fundamental para que el profesor cuente con los conocimientos necesarios que hagan de su práctica novedosa y efectiva, pues esta es una de las competencias con las que deben contar los profesores del siglo XXI (UNESCO, 2017; OCDE, 2019). Con la implementación de este tipo de herramientas se apunta a transformar los sistemas de educación y mejorar los resultados de aprendizaje en los educandos, por lo que el papel del profesorado es clave en la consecución de ese objetivo.
Por su parte, en el campo de la educación matemática, los modelos de Shulman (1986), Ball et al. (2008), Fennema y Franke (1992) y Rowland, Huckstep y Thwaites (2005), Godino (2009), entre otros, en su búsqueda de definir las características que tiene el licenciado en matemática y que lo hace diferenciar de otros profesionales con conocimiento de la matemática, pero sin el título en educación, intentaron describir el conocimiento especializado con el que debe contar el profesor que enseñe esta área del conocimiento, no solo desde lo didáctico-pedagógico, sino de la matemática misma (Acevedo-Rincón, 2020).
Sin embargo, es Carrillo et al. (2013) quienes profundizan sobre los modelos antes en mención y proponen el modelo conocimiento especializado del profesor de matemáticas, en inglés Mathematical Teacher's Specialised Knowledge (MTSK), cuyo eje central abarca dos dominios que caracterizan el conocimiento matemático y el conocimiento didáctico-matemático del profesor, y que a diferencia de los modelos anteriores es más específico en los subdominios de conocimiento disciplinar y de tipo didáctico-pedagógico con los que debería contar el profesor que enseña esta área. A su vez, este modelo cuenta con elementos que permiten analizar la práctica pedagógica de un profesor que enseña matemáticas mediadas por las TIC, por lo que se esperan relaciones entre los contenidos disciplinares de la matemática misma. En el caso de esta investigación de las secciones cónicas en geometría con el componente pedagógico del profesor, de manera que esté acorde a las exigencias del profesor de matemáticas de hoy día, donde utilice de manera efectiva las TIC en sus prácticas pedagógicas.
El modelo MTSK
Esta investigación tiene como fundamentación teórica el modelo del conocimiento especializado del profesor de matemáticas (MTSK), que describe el conocimiento matemático (MK) que requiere el profesor para enseñar matemáticas. Acorde con Carrillo et al. (2013) y Carrillo et al. (2018) comprende los conceptos, procedimientos, estructuras, ideas, conocimiento de las conexiones entre los conceptos, procedimientos, lenguaje matemático, entre otros, de manera que el profesor enseñe los contenidos relacionando sus conjeturas y las de sus estudiantes. Por su parte, el conocimiento didáctico-pedagógico del contenido (PCK) es el conocimiento del profesor en el proceso de enseñanza y aprendizaje de los contenidos de matemáticas (Vasco, 2015; Montes, 2015). Estos dominios de conocimiento se subdividen en tres subdominios cada uno como se observa a continuación:
De acuerdo con la figura 1, se tiene que en la parte izquierda del modelo se encuentra el dominio del conocimiento matemático (MK), que a su vez se desprende en tres subdominios que son: el conocimiento de los temas (KoT), conocimiento de las estructuras matemáticas (KSM) y conocimiento de las prácticas matemáticas (KPM). En la parte derecha del modelo, se ubican los subdominios pertenecientes al PCK que son: conocimiento de la enseñanza de las matemáticas (KMT), conocimiento de las características de aprendizaje de las matemáticas (KFML) y conocimiento de los estándares de aprendizaje de las matemáticas (KMLS). Aparte, en el centro se ubican las creencias y concepciones del profesor de la matemática como la forma en que se enseña la misma.
Subdominios del conocimiento matemático(MK).
Del dominio MK, se tienen los siguientes subdominios: (i) Conocimiento de los temas {KoT}, el cual se refiere a un conocimiento profundo y fundamentado de los contenidos concretos de matemáticas que el profesor quiere que aprenda el estudiante con niveles de profundización mayores. Dentro de este subdominio está incluido las categorías de procedimientos, definiciones, registros de representación, propiedades y relaciones fenomenológicas (Santana y Climent, 2015; Flores et al, 2014); (ii)Conocimiento de la estructura matemática {KSM), el cual corresponde al conocimiento del profesor acerca de cómo se relacionan elementos de diversos contenidos de la matemática en determinado momento concreto ligado a la enseñanza; de manera que estas relaciones simplifican o complejizan una temática en particular dentro del mismo campo de las matemáticas (Conexiones interconceptuales e intra conceptuales) (Montes y Climent, 2016); y, (iii) conocimiento de las prácticas matemáticas (KPM), es el conocimiento del profesor acerca de la forma en cómo se construye el conocimiento matemático, es decir la jerarquización y la planificación que se requiere para proceder a resolver problemas matemáticos, la validación y demostración de problemas matemáticos, el papel del lenguaje y los símbolos en matemáticas, prácticas particulares como la modelización y las condiciones que son necesarias para la generación de definiciones (Delgado & Zakaryan, 2019).
Subdominios del conocimiento didáctico-pedagógico del contenido (PCK).
En el dominio PCK, se tienen los siguientes subdominios: (i) Conocimiento de las características de aprendizaje de las matemáticas {KFML}, se refiere al conocimiento del profesor para identificar la interacción que tienen los estudiantes con los contenidos de las matemáticas abordados en las clases. Dentro de esto subdominio se incluye, las debilidades que tienen estos en el aprendizaje de los contenidos, los obstáculos que conllevan a que los estudiantes aprendan los contenidos de las matemáticas, el conocimiento de los intereses, gustos y motivaciones de estos para con las matemáticas y el conocimiento de teorías del desarrollo cognitivo de los estudiantes que son construidas a partir de las experiencias del quehacer de la práctica pedagógica de los profesores o teorías que son institucionalizadas dentro de la Educación Matemática (Carrillo et al., 2018); (ii) Conocimiento de la enseñanza de las matemáticas {KMT}, es el conocimiento que utiliza el profesor para representar los contenidos mediante recursos, actividades, tareas, ejemplos y su potencialidad en la enseñanza de las matemáticas. Apoyado en teorías derivadas de resultados de investigación en Educación Matemática o de su propia experiencia docente (Santana y Climent, 2016; Flores et al, 2014); y, (iii) Conocimiento de los estándares de aprendizaje de las matemáticas {KMLS}, se refiere al conocimiento del profesor acerca de lo que espera aprenda un estudiante en determinado grado de escolaridad, así como el nivel de profundidad con el que debe ser abordado un contenido en matemáticas a partir de referentes internacionales y nacionales como El Programa para la Evaluación Internacional de Alumnos (PISA, por sus siglas en inglés) y El Instituto Colombiano para la Evaluación (ICFES) que evalúan el desempeño por competencias de los estudiantes.
De este modo, este modelo es considerado en esta investigación debido al contexto en que esta se desarrolla con respecto al conocimiento especializado de un profesor de matemáticas que enseña secciones cónicas utilizando las TIC. Por lo que se espera que dicho conocimiento se evidencie en los subdominios del MTSK, particularmente se centra el análisis en elementos donde el profesor haga uso de herramientas TIC en el salón de clases.
Materiales y Métodos
Esta investigación tiene un enfoque cualitativo (Stake, 2005), ya que busca interpretar, analizar y describir el conocimiento especializado del profesor cuando enseña las secciones cónicas utilizando las TIC, específicamente la enseñanza de la elipse. La cual se desarrolla bajo un diseño de estudio de caso de tipo instrumental (Stake, 2005), puesto que a partir del estudio de una situación particular se pretende comprender la realidad que implica enseñar matemáticas escolares haciendo uso de las TIC en el aula de clase. Las técnicas de recolección de la información utilizadas en estas investigación son: (i)cuestionario de caracterización del conocimiento del profesor de matemáticas en TIC, el cual fue aplicado previo a las observaciones de clases, para así identificar al participante como potencial de esta investigación; (ii) observación no participante durante 13 sesiones; (iii) diario de campo; (iv) análisis de la observaciones no participantes realizadas, algunas de manera presencial y otras en la modalidad virtual y/o remota.
Este estudio se llevó a cabo en una institución de carácter privado de la ciudad de Barranquilla-Colombia, en el grado décimo de secundaria. La selección del caso se realizó a partir de un conjunto de casos relacionados con el tema de interés de esta investigación (Simons, 2011). Teniendo en cuenta el nivel de experticia del profesor con el software GeoGebra durante 3 años y de resultados de investigación como artículos y ponencias donde ha utilizado este y otros elementos TIC. Por su parte, las unidades de grabación y observaciones realizadas fueron acorde a las planificaciones previamente diseñadas por el profesor.
Ahora bien, para términos de esta investigación se seleccionaron los episodios en los cuales el profesor utilizó GeoGebra, incluyendo los contenidos de secciones cónicas. Sin embargo, para este artículo en particular, fue seleccionado un episodio relacionado con la gráfica de la elipse a partir de su ecuación general, su centro en y sus propiedades. En esta, el profesor propone actividades que permitan modelar lo anterior en GeoGebra para una mejor comprensión de los conceptos. De modo que se tuvo en cuenta para el análisis de este artículo las prácticas pedagógicas y matemáticas del profesor, objeto de análisis de esta investigación. Por lo que, los cuestionamientos, preguntas e inquietudes realizadas por los estudiantes solo contribuyen para enriquecer las respuestas del profesor y confirmar el dominio disciplinar y pedagógico o no del profesor en la enseñanza del tópico de secciones cónicas.
Resultados
El episodio que se presenta a continuación fue desarrollado con estudiantes de décimo grado de educación media secundaria. En este el profesor Pablo (seudónimo) muestra indicios de conocimientos del KoT, específicamente las categorías que corresponden a definiciones, procedimientos y propiedades de la elipse en la modelación de su respectiva gráfica. Además, se evidencia conocimientos del profesor acerca del nivel de potencialidad del recurso (GeoGebra) y la forma en cómo se enseña la elipse, categorías del KMT como se observa en el siguiente diálogo que sostiene Pablo y sus estudiantes (nombrados con una letra mayúscula del abecedario con el objetivo de diferenciar cada una de las participaciones en la clase).
| Pablo | OK jóvenes, vamos a solucionar el siguiente ejemplito, dice: determinar la ecuación de la elipse con centro en C= (-1,3), eje focal paralelo al eje x, eje mayor de 8 unidades y eje menor de 6 unidades, luego realiza la gráfica. Como tenemos que el centro es igual a C = (-1,3), entonces yo puedo decir que h = -1 y k = 3, además el eje mayor es igual a 8 [pausa], entonces recordemos que el eje mayor su longitud es igual a 2a 2a, entonces 2a = 8. Por lo tanto, yo puedo despejar el valor de a=4, porque el 2 que estaba multiplicando pasa a dividir. Análogamente hacemos lo mismo con el eje menor, recordemos que su longitud es igual a 2b, entonces yo puedo decir que 2b= 6 y b = 3 |
| Pablo | Entonces recordemos también que al ser el eje focal paralelo al eje x los vértices serían igual a: v 1 =(-1-4,3) y v 2 =(h + a,k) y v 2 - (h + a,k), entonces me queda lo siguiente: v t = (-1 - 4,3) y v 2 = (-1 + 4,3), es decir, v 1 = (-5,3) y v 2 = (3,3). V1 = (-5,3) y V2 = (3,3). |
| Pablo | Lo que hice fue reemplazar los valores, el valor de k que lo habíamos obtenido, el valor de a a también que era 4 a partir de los datos que me brindó el ejercicio. Para los puntos de corte con el eje normal, teníamos lo siguiente, eso está dado por B 1 =(h ,k - b) y B 2 = (h,k + b), donde h es -1. Y, k y a lo obtuvimos, ¿cómo?, el dato original 3, menos el valor de b que lo obtuvimos aquí [longitud del eje menor cuando el eje focal es paralelo a x. Entonces me queda aquí B 1 = (-1,3 - 3), y B 2 = (-1,3 + 3), y si resolviéramos eso me queda B 1 (-1,0) y B 2 = (-1,6). Ahora, ¿recuerdan por dónde debe pasar el eje focal en un vértice (h, k)? |
| Estudiante B | ¿No eran los focos (h,k - c) y (h,k + c)? |
| Pablo | OK, teníamos lo siguiente eje focal va a estar dado por mi componente de mi centro y y ¿quién es mi componente en y de mi centro? |
| Estudiante B | 3 |
| Pablo | Es decir, por k = 3, como lo queramos poner, sabiendo que eso va a ser una asíntota vertical. Ojo, aquí pongo y = k, esto es una igualdad, puede utilizar fe = 3, teniendo en cuenta que no importa las dos constantes que coloquemos, simplemente por ahí debe pasar una asíntota. |
| Estudiante B | Mr. y ¿Cómo encuentras la c ? |
| Pablo | Ah OK, recuerda la c que nosotros utilizábamos a 2 + b 2 y de ahí la despejamos, el teorema de Pitágoras. |
| Pablo | Ahora nos falta c, ¿cómo la encuentro? [pausa] ¿Así b 2 + c 2 = a 2 ? |
| Pablo | ¿Cómo despejo el valor de c, teniendo ya el valor de a y b? |
| Estudiante D | Pasas la b a restar |
| Pablo | ¿así c 2 = a 2 -b 2 |
| Estudiante D | ¡Sí! |
| Pablo | OK, pero como yo quiero es el valor de c y no c 2 , ¿qué debo hacer? [Pausa], saco raíz cuadrada en ambos miembros y ¿qué me queda? |
| Estudiante B | Queda 2 √a 2 - b 2 √a 2 -b 2 = c |
| Pablo | OK, entonces ya yo tengo el valor de a y b, a=4 y b=3 y ahora entonces reemplazo 2 √4 2 - 3 2 , ¿cuánto es 4 2?4 2? |
| Estudiante B | 16 |
| Pablo | OK, díganme el desarrollo de eso |
| Estudiante B | 2 √16 - 9 |
| Pablo | OK, ¿cuánto me da en definitiva? |
| Estudiante C | 7, raíz de 7 |
| Estudiante B | ¿Y eso no da una raíz inexacta?, ¿cuál es la raíz de 7? |
| Estudiante D | 2.64 |
| Pablo | c = 2.64 |
| Pablo | Entonces ya tengo como encontrar las componentes de mi foco, ¿cómo Mr.? [Pausa], míralo aquí F 1 = (h - c, k) y F 2 =(h + c,k), entonces queda: F 1 = (-1 - √7,3)pongo √7, para cuando realice toda la operación me tome todos los decimales y F 2 = (-1 + √7,3) Ahora me dicen ¿cuánto les da la suma del F 1 ?, digo suma porque son signos iguales |
| Estudiante C | Da -3,64. |
| Pablo | OK. Así: F 1 = (-3.64,3) |
| Pablo | ¿Y F 2 ? |
| Estudiante B | 1.64 |
| Pablo | O sea positivo, F 2 = (1.64, 4) |
| Pablo | Ahora, teniendo todo lo que encontramos, ¿qué es lo que me hace falta? [Pausa], lo que me están pidiendo Mr. |
| Estudiante B | Escribir la ecuación |
| Pablo | Entonces, recordemos que como es una elipse horizontal, utilizó esta ecuación: 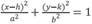 Luego realizó la respectiva sustitución en la ecuación, entonces ¿quién es x?, nada Mr., eso hace parte de la ecuación, pero si tenemos el valor de
h,
¿quién es
h?
-1 y
k
es 3. Luego realizó la respectiva sustitución en la ecuación, entonces ¿quién es x?, nada Mr., eso hace parte de la ecuación, pero si tenemos el valor de
h,
¿quién es
h?
-1 y
k
es 3. |
| Pablo | Entonces queda así:  , ojo en el caso de
h,
debes tener cuidado con el menos de la fórmula y el menos del signo de
h,
por su parte en
k
no tengo necesidad de poner paréntesis al ser positivo, ¿hasta ahora es claro de donde saco los datos? [pausa] de mi centro , ojo en el caso de
h,
debes tener cuidado con el menos de la fórmula y el menos del signo de
h,
por su parte en
k
no tengo necesidad de poner paréntesis al ser positivo, ¿hasta ahora es claro de donde saco los datos? [pausa] de mi centro |
| Estudiante B | Sí |
| Pablo | Ahora ¿quién es el valor de a? |
| Estudiante B | 4 |
| Pablo | ¿y el de b? |
| Estudiante B | 3 |
| Pablo | Y me queda  , es decir, prácticamente tengo mi ecuación lista, ¿porqué digo casi?, porque debo desarrollar el denominador, entonces tenemos 4
Z
4
2es ¿cuánto es? , es decir, prácticamente tengo mi ecuación lista, ¿porqué digo casi?, porque debo desarrollar el denominador, entonces tenemos 4
Z
4
2es ¿cuánto es? |
| Estudiante C | 16 |
| Pablo | OK, y ¿menos por menos en el numerador? |
| Estudiante C | Más |
| Pablo | 32 es 9. Y me queda  , ahora como yo quiero realizar la gráfica de la ecuación voy a utilizar a GeoGebra, entonces copio la ecuación a la que llegamos y me la traigo para acá [GeoGebra] para hacer su respectiva gráfica y ahí me proyecta la gráfica (Figura 2). Ahora verifiquemos que los datos que encontramos eran precisos, ¿cuál es mi centro? , ahora como yo quiero realizar la gráfica de la ecuación voy a utilizar a GeoGebra, entonces copio la ecuación a la que llegamos y me la traigo para acá [GeoGebra] para hacer su respectiva gráfica y ahí me proyecta la gráfica (Figura 2). Ahora verifiquemos que los datos que encontramos eran precisos, ¿cuál es mi centro? |
| V1Estudiante B | (-1,3] |
| Pablo | OK, y nosotros encontramos v 1 que es (-5,3) y miren cómo va apareciendo aquí [en GeoGebra] y , v 2 ¿quién es? |
| Estudiante B | (3,3] |
| Pablo | OK, ahora bien, los puntos de corte ¿con el eje quién? |
| Estudiante B | x |
| Pablo | Los puntos de corte con el eje normal (y), con el eje x los vértices, ¿quiénes eran? B 1 = (-1,0) y ¿ B 2 ? |
| Estudiante C | ¿no era (-1,6)? |
| Pablo | B2= (-1,6) y aquí (obsérvesefigura 3flechas de color negro) graficamos todo lo que hayamos encontrado. |
| Pablo | Ah OK, y me hace falta lo principal [pausa], ¿qué es lo principal de una elipse? [Pausa], sus focos ¿si recuerdan? |
| Estudiante B | Sí |
| Pablo | El F 1 = (-3.64, 3), pero eso va a ser una aproximación ya que -3.64 tiene más decimales, mírenlo ahí [puntos E y F ] y el = (1.64, 3) y ahí tengo todos los valores de mi elipse, mírenlo ahí , , , , B 1 , B 2 , puntos de corte con el eje normal y esta historia continuará (...) |
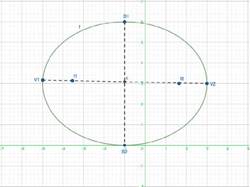
Fuente: Elaborado por los autores
Figura 2 Gráfica de los vértices, focos y puntos de corte con el eje normal de la elipse en el software GeoGebra.
En este apartado se resalta que Pablo evidencia conocimiento de las propiedades que enseña, ya que al proponer un ejercicio a los estudiantes relacionado con el gráfico de una elipse con centro en (h, k) es decir que no parte del origen, este sabe que los datos que brinda el ejercicio de que el eje focal es paralelo al eje x, eje mayor de 8 unidades y eje menor de 6 unidades, partes de la elipse pueden ser utilizados de manera efectiva en la solución del ejercicio que apunta a la gráfica de la cónica y al cálculo de las coordenadas de los vértices (VI, K2) y del eje menor (B 1 y B 2 ). De igual manera muestra indicios de conocimientos de las definiciones, categoría del KoT ya que al utilizar la propiedad de que el eje focal es paralelo al eje x, este sabe que lo anterior implica que los vértices y el eje menor estén definidos de manera diferente a cuando una elipse tiene centro en el origen. Siendo a su vez llamativo que Pablo utiliza esta definición para relacionarla con otra definición derivada de elipses con centro en (h , k). Esto es, que sabe que toda elipse con esta forma en su centro contará con una asíntota vertical al eje focal.
Por su parte, es interesante que un estudiante pregunta a Pablo por ¿cómo calcular el valor de c?, el cual es necesario en el análisis del cálculo de la ecuación general de la elipse que tiene forma
 -=1,a>b> 0,
y
a
2
= b
2
+ c
2
,
centro de interés de la clase.
-=1,a>b> 0,
y
a
2
= b
2
+ c
2
,
centro de interés de la clase.
Se intuye que esta pregunta surge, dado que a percepción del estudiante lo ahondado inicialmente por Pablo no correspondía a lo que se pretendía desarrollar en la clase que era: cálculo de la ecuación general de la elipse con centro en (h, k) y su respectiva gráfica. Por lo que se comprueba que Pablo conoce que las definiciones y propiedades son el camino correcto para solucionar lo solicitado en el ejercicio. Por eso realiza preguntas a los estudiantes como: ¿recuerdas que la c se calcula del teorema de Pitágoras?, lo que es llamativo, puesto que Pablo sabe que para calcular cada elemento que permita solucionar el ejercicio se debe pasar por procedimientos conexos al que se está desarrollando.
De esta manera muestra indicios de conocimientos de procedimientos, categoría del KoT ya que sabe que para despejar el valor de C en la ecuación a 2 = b 2 + c 2 con forma en el teorema Pitágoras debe aplicar operaciones matemáticas previamente, por lo que realiza preguntas a sus estudiantes como: ¿qué debo hacer? ¿Si saco raíz en ambos lados de la ecuación qué me queda? Que son orientadoras para que los estudiantes reemplazan los valores de a y b hallados en cálculos anteriores y sean ellos quienes procedan en lo que se busca, como por ejemplo en los cálculos de potencias y raíces, contenidos que resultan del mismo procedimiento inicial y que Pablo conoce, lo que se comprueba cuando pregunta ¿cuál es el desarrollo de √(16-7) ?, expresión que termina determinando el valor de c.
Por otro lado, y de manera simultánea en la clase se observan muestras de conocimiento de Pablo acerca de las categorías de definiciones y procedimientos del KoT, específicamente cuando identifica la fórmula de la ecuación que debe utilizarse dado que la elipse tiene forma horizontal, de igual manera el procedimiento que se debe realizar para al reemplazar los valores de las variables a, b y c en la ecuación de la elipse, lo cual incluye el conocimiento de Pablo del desarrollo de potencias y la ley de los signos de los números reales.
A su vez, Pablo muestra indicios significativos del conocimiento de potencialidad del recurso para la enseñanza, categoría del KMT, dado que conoce que GeoGebra le permite graficar las secciones cónicas a partir de su ecuación general. Por lo tanto, les pide a los estudiantes que realicen el gráfico de elipse con ecuación
 , ya que sabe que, de manera visual, es más probable que los estudiantes identifiquen de manera gráfica las partes que componen la elipse, como los focos, el centro, vértices, coordenadas del eje menor, puntos de intersección con el eje x y con el eje normal. Lo que se comprueba con preguntas de verificación que Pablo realiza como: ¿cuál es el centro?, ¿Cuáles son los puntos de corte? y preguntas que denotan su conocimiento acerca de estrategias para la enseñanza de las matemáticas como: ¿cuáles son los elementos principales de una elipse? Que se intuye Pablo realiza posterior al gráfico de la elipse para que teniendo en cuenta todos los elementos que componen esta, no pierdan de vista que la definición de la elipse está arraigada a la suma de las distancias de los puntos
P(x,y)
a dos puntos fijos llamados focos, pero en este caso analizado desde la observación del gráfico de GeoGebra que representa a una elipse con centro en
(h, k).
Además, pablo, tiene también conocimiento de la potencialidad del recurso GeoGebra para por medio de sus comandos notar el punto exacto en el que está ubicado los vértices (eje x), puntos de corte con el eje normal (eje y) los focos y las coordenadas del eje menor como se observa en la figura 3.
, ya que sabe que, de manera visual, es más probable que los estudiantes identifiquen de manera gráfica las partes que componen la elipse, como los focos, el centro, vértices, coordenadas del eje menor, puntos de intersección con el eje x y con el eje normal. Lo que se comprueba con preguntas de verificación que Pablo realiza como: ¿cuál es el centro?, ¿Cuáles son los puntos de corte? y preguntas que denotan su conocimiento acerca de estrategias para la enseñanza de las matemáticas como: ¿cuáles son los elementos principales de una elipse? Que se intuye Pablo realiza posterior al gráfico de la elipse para que teniendo en cuenta todos los elementos que componen esta, no pierdan de vista que la definición de la elipse está arraigada a la suma de las distancias de los puntos
P(x,y)
a dos puntos fijos llamados focos, pero en este caso analizado desde la observación del gráfico de GeoGebra que representa a una elipse con centro en
(h, k).
Además, pablo, tiene también conocimiento de la potencialidad del recurso GeoGebra para por medio de sus comandos notar el punto exacto en el que está ubicado los vértices (eje x), puntos de corte con el eje normal (eje y) los focos y las coordenadas del eje menor como se observa en la figura 3.
Discusión
En el episodio seleccionado, es evidente que los subdominios del MTSK donde más indicios de conocimiento por parte del profesor se muestran son en el KoT y KMT, siendo este último donde se muestra más el conocimiento especializado del profesor para enseñar la elipse de manera efectiva utilizando las TIC, en este caso utilizando el programa de office Power Point y el software GeoGebra como recursos. Lo cual está alineado con las investigaciones realizadas por Padilla-Escorcia y Acevedo-Rincón (2020) y Padilla-Escorcia y Acevedo-Rincón (2021) en las cuales se encontraron dentro de los hallazgos que para el profesor poder enseñar las funciones trigonométricas haciendo uso de recursos tecnológicos como GeoGebra requiere de su conocimiento tanto disciplinar como de tipo pedagógico. De igual manera, en los hallazgos de Santana y Climent (2015) se evidenció que para la enseñanza de la geometría haciendo uso de GeoGebra, es necesario que el profesor tenga conocimiento del tema que enseña, así como de la forma en cómo enseñanza tal contenido y la forma en cómo aprenden sus estudiantes.
En las observaciones realizadas en la presente investigación, el profesor muestra dominio e indicios de algunos indicadores del MTSK. En particular del subdominio KoT, los indicadores que más se evidencian en esta investigación son saber usar la definición de elipse y conocer los procedimientos de contenidos de la elipse. A partir de esto, se le facilita poder calcular la ecuación general de la elipse de acuerdo con la forma en como esté definida esta, bien sea de manera horizontal o vertical o también de acuerdo con su centro, en el origen o con forma en (h,k ). Pablo muestra acercamientos profundos entre relaciones que establece entre las definiciones de la elipse, como se menciona en el indicador del MTSK, ya que a partir del dominio de las definiciones anteriores añade nuevas definiciones como por ejemplo la definición de vértice con forma v 1 = (h - a,k) y v 2 = (h + a,k) y ejes menores con forma B 1 = (h,k - b) y B 2 = (h,k + b), lo cual se deriva de que Pablo conoce que estas definiciones pueden ser aplicadas siempre que la elipse no tenga centro en el origen, como se muestra en el episodio analizado en esta investigación.
No obstante, es importante resaltar que la categoría de definiciones del subdominio KoT está conectada a la categoría de procedimientos y que por lo tanto estos indicadores del MTSK depende uno del otro para que realmente sean efectivos en el conocimiento del profesor, ya que como se evidencia en este episodio Pablo sabe las definiciones, pero también conoce cuales son los procedimientos a seguir al utilizar esas definiciones, un claro ejemplo es la elipse horizontal propuesta por Pablo en clase y con forma
 a >b > 0, y
a
2
= b
2
+ c
2
,
este sabe que el procedimiento a seguir al aplicar esa definición para calcular el valor de c, donde es fundamental en el cálculo de los focos de la elipse, el teorema de Pitágoras, siendo que en el desarrollo de este se usan procedimientos matemáticos que relacionan la potenciación, radicación y ley de signos. Es decir que podría formularse preguntas de este tipo el profesor: ¿cómo calcula el valor de c, coordenada de los focos de la elipse a partir de la definición de esta?, siendo estas preguntas orientadoras para el desarrollo del ejercicio que plantea inicialmente.
a >b > 0, y
a
2
= b
2
+ c
2
,
este sabe que el procedimiento a seguir al aplicar esa definición para calcular el valor de c, donde es fundamental en el cálculo de los focos de la elipse, el teorema de Pitágoras, siendo que en el desarrollo de este se usan procedimientos matemáticos que relacionan la potenciación, radicación y ley de signos. Es decir que podría formularse preguntas de este tipo el profesor: ¿cómo calcula el valor de c, coordenada de los focos de la elipse a partir de la definición de esta?, siendo estas preguntas orientadoras para el desarrollo del ejercicio que plantea inicialmente.
De igual manera, el indicador correspondiente a saber usar las definiciones de elipse también muestra relación directa con el indicador saber los registro de representación para notar una elipse, esto se entiende desde que para poder representar gráficamente una elipse, como bien es el objetivo de la clase que propone Pablo en GeoGebra, se requiere que se conozca a profundidad ¿cuál es el tipo de elipse que se busca graficar?, por lo que es interesante cuestionamientos por parte del profesor cómo: ¿qué se requiere para graficar una elipse? ¿Qué determina de manera gráfica que la elipse sea horizontal o vertical? ¿En qué varía en el gráfico de una elipse que esta no parta del origen? Es interesante que precisamente el saber de las definiciones de la elipse son claves para comprender la gráfica de una elipse a partir de su ecuación general. Lo que resulta llamativo en cuanto a que Pablo parte de las definiciones de la elipse para su respectiva gráfica denotada como registro de representación.
Ahora, en cuanto al indicador referente a saber de las propiedades y fundamentos de la elipse. Pablo muestra indicios de que conoce de estas, ya que en el ejercicio que se plantea en este episodio correspondiente al cálculo de la ecuación general de una elipse con centro en (h, k) para realizar su respectiva gráfica. Este utiliza los datos que brinda el ejercicio del eje menor y mayor de la elipse para calcular los valores de a y b, variables presentes en la fórmula de la ecuación general. Siendo llamativo que este indicador también muestra relación con el indicador de saber las definiciones de la elipse, lo cual se intuye dado que para el profesor poder utilizar las propiedades del eje mayor y menor de una elipse con centro en (h, k) debe saber que estas le permiten encontrar las incógnitas necesarias para calcular la ecuación de la elipse, es decir saber la definición exacta de la ecuación de la elipse cuando su centro no parte del origen.
Por otro lado, en el subdominio KMT, Pablo muestra indicios del indicador del MTSK correspondiente a saber el nivel de potencialidad de recursos materiales y virtuales en la enseñanza de la elipse. Especialmente del software GeoGebra como recurso para visualizar de manera gráfica la elipse con ecuación general hallada en el ejercicio solicitado, además de manera simultánea la ubicación en la gráfica de cada una de las partes de la elipse que permitieran a los estudiantes verificar que los resultados obtenidos de manera analítica corresponden a los mismos de manera gráfica, así como las respectivas distancias entre estos. Lo que a su vez está alineado con lo manifestado por Pablo en el cuestionario con respecto a que utiliza GeoGebra en sus clases puesto que puede utilizarse en muchas áreas de la matemática, como es en este caso de la geometría, Pablo se notó convencido con respecto a que con este software los estudiantes pueden visualizar mejor la abstracción que consigo llevan las matemáticas de manera dinámica y modelada, lo que hace notar que Pablo mantiene concordancia con lo que expresa en sus comentarios y la realidad encontrada en el aula.
A partir de lo anterior, es interesante que el indicador del KMT saber el nivel de potencialidad de recursos materiales y virtuales en la enseñanza de la elipse, guarda relación con el indicador del KoT saber las definiciones de la elipse. Llamando la atención que dentro del MTSK se presentan micro esquemas entre subdominios y dominios distintos del modelo. Entendiendo esto desde la mirada que es necesario saber las definiciones de las coordenadas de cada una de las partes de la elipse como los vértices, focos entre otros, para luego visualizar las mismas de manera gráfica, de manera que el conocimiento de las definiciones es clave para a partir de GeoGebra éstas sean verificadas. Por esta razón se considera que Pablo sabe lo que dispone este software en cada uno de sus comandos, pero más allá de eso sabe también que a partir del mismo es la mejor manera de que los estudiantes apliquen las definiciones teóricas concernientes a la elipse.
No obstante, Pablo muestra versatilidad en el uso de herramientas TIC en la enseñanza de las matemáticas, esto pues, muestra indicios del indicador saber el nivel de potencialidad de recursos materiales y virtuales en la enseñanza de la elipse, ya que por medio del programa office, específicamente de sus comandos de resaltado y de colores. Este aprovecha que este episodio de clase se da bajo las condiciones de la modalidad remota para que los estudiantes mediante animaciones diferencien los datos conocidos que ofrece el ejercicio, lo que denota que Pablo no utiliza esta herramienta (Power Point), solamente como un medio que proyecta diapositivas, sino que interactúa en estas en búsqueda de mejores comprensiones del estudiantado.
Por otra parte, cabe destacar que a pesar de que no fue incluido dentro de los subdominios de análisis, es preocupante que Pablo no promueve al indicador de notación de la matemática del KPM, dado que utiliza términos como "pasar este término del otro lado", "pasar a sumar o restar" y "pasar a multiplicar o dividir", lo cual no es un lenguaje acorde a las prácticas matemáticas. El profesor debería utilizar terminologías como el inverso multiplicativo y el inverso aditivo como procesos que influyen en el despeje de una ecuación, o en su defecto, asumir que los estudiantes comprenden que el pasar del otro lado involucra que la operación propuesta corresponde al inverso. Esto es, de "estar multiplicando un número o término", puede anularse este término si toda la expresión se divide por el mismo número o término, lo que finalmente resulta en primera instancia, la anulación de términos (inversos) y, posteriormente, en la división del término. Lo anterior promueve un lenguaje que remite a la formalidad en el aprendizaje de los conceptos por parte de los estudiantes.
En síntesis, la Tabla 1 resume el conocimiento especializado del profesor para la enseñanza de la elipse haciendo uso de recursos tecnológicos como GeoGebra y Paint. Es interesante que las evidencias de conocimiento encontradas en Pablo hacen referencia al KoT y al KMT. En la Tabla 1 se cita también el # de la clase en que se hizo evidencia de tal conocimiento con su respectiva justificación. Esto a su vez muestra que es necesario que el profesor que enseña la elipse requiere no solamente de conocimiento disciplinar, sino también de tipo didáctico y pedagógico para poder hacer un buen uso de las TIC con fines de enseñanza.
Tabla 1 Evidencias de conocimiento de Pablo del KoT y KMT durante las unidades de observación en la enseñanza de la elipse
| #clase | Dominio y subdominio identificado | Justificación |
|---|---|---|
| 5 | MK- KoT PCK-KMT | Conocimiento del profesor para calcular la ecuación general de la elipse y realizar la modelación gráfica de esta mediante el software especializado GeoGebra. Conocimiento del profesor para realizar la modelación gráfica de la elipse, dado las partes de la elipse. Conocimiento del profesor para representar empíricamente a la elipse mediante el programa Paint. |
| 6 | MK-KoT PCK-KMT | Conocimiento del profesor para calcular las variables a, b y c de la ecuación general de una elipse. Conocimiento del profesor para graficar la elipse como estrategia para verificar los resultados de las partes de la elipse de manera teórica. |
| 7 | PCK-KMT | Conocimiento del profesor para construir una elipse empírica con material concreto como ejemplificación de la definición teórica de esta sección cónica |
| 9 | MK - KoT PCK-KMT | Conocimiento del profesor para calcular la excentricidad de una elipse y verificar el resultado mediante los comandos del software GeoGebra. |
| 9 | MK - KoT PCK-KMT | Conocimiento del profesor para calcular el eje focal y eje normal de una elipse y verificar los resultados teóricos de estos de manera práctica mediante los comandos del software GeoGebra como herramienta TIC. Conocimiento del profesor para calcular los vértices y puntos de corte con el eje normal de una elipse y su respectiva verificación de manera práctica mediante el software especializado GeoGebra. |
| 10 | MK-KoT | Conocimiento del profesor para relacionar el eje mayor y eje menor de una elipse con el cálculo de las incógnitas de la ecuación general de la elipse. |
Fuente. Elaborado por los autores
Conclusiones
En esta investigación se dieron evidencias de los subdominios del KoT y KMT a partir de algunas de las categorías que las componen como: definiciones, procedimientos, propiedades y potencialidad del recurso, estrategia o tarea en la enseñanza de las matemáticas en el contenido de la sección cónica elipse mediante herramientas TIC como GeoGebra y Power Point. Con base en esto se comprobó que el profesor requiere de dominio conceptual de los contenidos que enseña, particularmente de las definiciones, ya que como se evidenció en este episodio para poder aplicar las propiedades y saber desarrollar procedimientos relacionados con la elipse, fue clave que este supiera la definición de elipse y su ecuación general para llevar a cabo el respectivo proceso gráfico de la elipse en GeoGebra y poder visualizar de manera práctica cada uno de estos contenidos como potencial en el proceso de aprendizaje de las matemáticas. Lo que es un índice fundamental dentro de los hallazgos de esta investigación es encontrar que el participante relaciona su conocimiento matemático con sus conocimientos didáctico-pedagógicos para la enseñanza de los contenidos de matemáticas utilizando las TIC.
Así mismo, de acuerdo con el conocimiento especializado del profesor evidenciado en esta investigación, algunas cosas podrían ser adaptadas a la formación de profesores de matemáticas, en general. Dentro de esto se destaca la metodología que utiliza el profesor para ahondar los contenidos, con preguntas que no son inducidas, sino que por el contrario conllevan a que el estudiante se cuestione y a través del diálogo realice cada uno de los procedimientos que el profesor ya conoce y sabe cómo desarrollar y por lo tanto intervenir en momentos puntuales para darle mayor fluidez en el proceso de aprendizaje de los estudiantes. Así mismo, que los indicadores propuestos en esta investigación para los subdominios objetivo de análisis sean referencia para el profesorado si se pretenden enseñar contenidos de matemática mediados por las TIC bien en software como GeoGebra o programas office como Power Point.
















