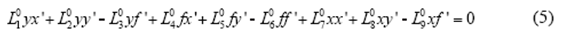Introduction

Relative orientation is the process of recovering the position and orientation of one image with the other in an individual image space coordinate system (L äbe & F ärstner, 2006), which is a classic topic in satellite photogrammetry, computer vision, and 3D model reconstruction. With the development of the study fields, a higher accuracy of relative orientation model is demanded and is a crucial process for ensuring and improving the accuracy of relative orientation. For the 3D measurement and space model reconstruction in the geological landslides, basing on multiple images, the accuracy of relative orientation directly determined the accuracy of the reconstructed 3D model, whose accuracy can reach the accuracy with the laser scanner in precision, theoretically. Therefore, the high-precision relative orientation model is a key point for the various applications basing on space relative orientation (^{Horn, 1990}; ^{Mikhail, Bethel & McGlone, 2001}).

Many attentions are concentrated on solving relative direction elementary with the linear methods, such as eight-point algorithm, five-point algorithm, and singular value decomposition (^{Longuet-Higgins, 1987}; ^{Philip, 1996}; ^{Faugeras, 1993}; ^{Hartley & Zisserman, 2003}). Longuet-Higgins was the first to discover that the position and orientation of one image with the other is contained in the essential matrix (Longuet-Higgins, 1987). In that paper, an eight-point algorithm is proposed to estimate an essential model with the limitation that it will introduce significant error because of noises in the image. To get the more definite essential matrix, ^{Nistér proposed five-point algorithm (Nistér, 2004}). The five-point algorithm estimates essential matrix by calculating the root of polynomial ten times. There are also methods on singular value decomposition (^{Taylor & Kriegman, 1995}; Ma, Soatto, Kosecka & Sastry, 2004; Hartley & Zisserman). Although homogeneous algebraic representation and singular value decomposition strategy can calculate relative direction elementary efficiently, it is a significant error in the result because of unmatched conjugate points. When there are outliers among the conjugate points, the least squares iterative method is one of the best choices for more accuracy results of relative orientation elementary. The least squares iterative method will decrease the adverse influence of the outliers by the iterative process.

In the calculation process for relative orientation parameters, there are two solving methods. One is using iterative calculation with the least square adjustment. The method needs to give the initial parameter value. However, the initial value cannot be provided in some case, and the range of the given initial value will affect the accuracy of the relative orientation (^{Stewenius, Engels & Nistér, 2006}). In the worst situation, the wrong initial value will cause the equation does not converge and then have no solution, especially at close range applications (^{Li, Liu & Tang, 2007}; ^{Pan, 1999}; ^{Duane, 1971}). For large rotation angle of close range images, more strict relative orientation method is adopted to restore their relative position (Tang & Heipke, 1994; ^{Werner, 2003}; ^{Zhang, Huang, Hu, Wan & Lin, 2011}). The other method is to solve the equation of relative orientation model with one or some accurate parameter value directly. For the case, it is also difficult to acquire the few specific value which constraints its application for some fields.

In this paper, a new relative orientation model, direct relative orientation with seven constraints is proposed to overcome the problems in the models described above. In the new model, the initial value is calculated by direct relative orientation with a rough Bx. Then, the seven constraints are used to control and adjust the solved parameter result during the bundle block adjustment. Six constraints are derived from the inherent orthogonal property of rotation matrix. The seventh constraint stems from the decomposition of baseline. In the experiment, the model correction is validated, and the space position assesses the accuracy. Through the experimental result, it is revealed that the proposed new model can improve and acquire a higher accuracy of relative orientation, and is suitable for large oblique angles and translation using the multiple images to measure geological landslides and perform 3D reconstruction of the geological landslides.

Conventional model of relative orientation

1. Coplanarity condition equation

Relative orientation is the process of recovering the position and orientation of one image with the other in an individual image space coordinate system. Given two images (left and right images) with an overlap filed from different viewpoints, a stereo model can be created and reconstruct the original epipolar geometry, represented by Figure 1. Assuming a ground point M is imaged at two viewpoints S1 and S2, the two image points (m1 and m2) are acquired, and the corresponding imaged ray is R1 and R2 respectively. The vector distance between the two viewpoints is called baseline B. Basing on the epipolar geometry, the vectors R1, R2, and B must be in one plane, coplane, whose mathematical expression is represented by Equation 1.

Figure 1 The diagram of the epipolar geometry relationship in the stereo images. 

Basing on the epipolar geometry, the mathematic model of relative orientation can be expressed as follow by coplanarity Equation 3 and Equation 17 according to Equation 1.

where Bx, By, Bz are components of baseline of a stereo pair [X1 Y1 Z1]=[x y -f]T and [X2 Y2 Z2]=R[x y -f]T coordinates of conjugate points in the image space coordinate system, (x,y) and (x',y') represent conjugate points in the image space coordinates system, the rotation matrix

Composes of the three angles and f the focal length of image, respectively. The BX, BY, BZ represents the component of baseline in X, Y, Z directions, respectively.

2. Direct relative orientation model

In aerial photogrammetry, the values of BY, BZ, are set to zero as the initial value, and the accurate value of BX is given to determine the scale of the stereo model; otherwise the model scale will be any size. However, the initial value of the baseline components (BY, BZ) and the rotation angles is unknown in some cases, which will result in a low accuracy or an error solution for relative orientation. For this case, direct relative orientation model can be used to calculate the orientation parameters and perform the relative orientation. For the model of direct relative ordination, the value BX needs to be fixed accurately, and then the model derives to a linear mathematic construct for calculating the other parameters of relative ordination. The direct relative orientation can avoid the iteration calculation in the least square adjustment owing to the linear mathematic construct. However, two sets of parameter result for the relative ordination can be acquired, and need to determine which one is true.

According to the space image coordinate of the left and right image point, the coplanarity condition equation Eq.(2) can be transformed into the following linear form of Eq.(3).

In the Eq. (3), the ^{_{L , L2,}} L₃, L , L₅, L₆, L L₈, L are the polynomial coefficients which are described in Eq. (4), respectively.

Eq. (5) is obtained by Eq. (3) dividing ^_L5 on both sides.

Where L ⁰;= L;/L₅, L⁰ ₅ = 1. Eq. (5) is the basic mathematic model of direct relative orientation. This model can directly calculate the eight unknowns, ^_L01 , ^_L02 , ^_L03 , ^_L04 , ^_L05 , ^{_{L06 L07 L08 L09}} with eight or more conjugate points without approximate values.

The baseline parameter BX has no influence on building up a stereo model; it can be assumed to be known. Therefore, parameters BY and BZ are obtained by the following equations:

The following equations can get nine elements of rotation matrix R:

Finally, three rotation angles can be decomposed by the definition of R [3, 17].

According to Eq. (6), L5 can be positive or negative, which does not affect the values of B _Y and B _Z. However, there are two sets of possible solutions for the rotation angles . One of the two solutions only can be used to acquire the real configuration of relative orientation. Therefore, the degree of the two angles and are used to determine and select a true solution, which should satisfy the following range represented in Eq. (9).

3. Model of direct relative orientation with constraints

During the conventional model of direct relative orientation, the eight parameters ^_L01. L⁰ ₂, ^_L03, L⁰ ₄, L⁰ ₆, L⁰ ₇, L⁰ ₈, L⁰ ₉ can be calculated when the value of BX is fixed. It is evident that the Eq. (3) is linear, so the values of eight parameters can be determined uniquely without the parameters correlation. For the model, the parameters of rotation R and baseline B in the relative orientation are only constrained by the model equation, but not constrained by the relationship among the parameters, which will decrease the accuracy and stability of the parameter result and then reduce the accuracy of relative orientation.

In the computer vision, it is well known that epipolar equation x'^TEx=0, rank-two constraint det(E)=0, and trace constraint 2EE^TE-trace(EE^T)E=0 are utilized to solve essential matrix E. In the epipolar equation, the x' and x represent the normalized image coordinates of conjugate points from the left and right images, respectively. The essential matrix E can be calculated through the matrix multiplication between the translation T and rotation R, E=TR. For the solving method, the nine components in the rotation R is constrained by orthogonal property of rotation matrix included implicitly in these equations. However, the elements in the baseline B are not limited. Also, the solving method in the computer vision yields nine homogeneous polynomial equations of degree 3, and the nine similar polynomial equations are correlated.

Different with the conventional model of direct relative orientation and the essential matrix in computer vision that normalized image points as observations, a new relative orientation model, direct relative orientation model with seven constraints, is proposed and validated. In the new model, the original image point coordinate of conjugate points and focal lengths f are used, and the constraint includes the components relationship in rotation R and baseline B for improving and ensuring the accuracy and stability of relative orientation. The seven constraints are represented by Eq. (10).

The proposed new model of direct relative orientation with seven constraints consisted of Eq. (2), (3) and (10). The model selects the initial nine parameters of direct relative orientation as unknowns, and seven constraints are considered to improving and ensuring the accuracy of the solved parameters.

4. Solution of direct relative orientation with constraints

In the process of calculation of parameters in direct relative orientation with constraints, assuming Eq. (2) is not equal to zero and an error v is in the equation, thus the Eq. (2) is derived to Eq. (11) basing on the Eq. (3).

Then, differential form of the Eq. (11) is represented by Eq. (12). The F0 is the approximate value of F, and ^{_{dBx, dBy}} ... ^{_{dc2, dc3}} is the variation of the 12 unknown parameters for relative orientation. Thus, the error equation is described as Eq. (13).

Where V, X, L represent the observation vector, parameter variation value, and the free vector, respectively.

To improve and ensure the accuracy of the solved parameters, the seven independent constraints described above, are considered, and its equation is expressed by Eq. (14).

B and W are the coefficient matrices and the observation vector of constraint condition in the bundle block adjustment, which are represented by Eq. (15) and Eq. (16), respectively.

Combining the error equation of observation and the equation of constraint condition, the error equation with constraint condition is expressed in Eq. (17).

According to the least square with restrictions, the 12 unknown parameters can be computed and express by the Eq. (18).

In the Eq. (18), the U, K , and Wu can be acquired by the follow Eqs. (19).

5. Experiments and results

Data and Experiment

The indoor close range images with large oblique angles are used for experiments to validate the correctness and accuracy of the proposed new model of direct relative orientation with seven constraints. The stereo image pair was acquired by a non-calibrated Sony IMX135 camera with a pixel size of 1.12 μm which is shown in Figure (2). The numerous conjugate points from the left and right image were detected using SURF match model, and the error match points were removed to obtain the reliable relative orientation results as is shown in Figure 3. From the 62 high-precision matched points, the six conjugate points were selected and used to validate the model correctness and assess the result accuracy of the relative orientation. The baseline length was measured as 0.55m.

Figure 2 The stereo images are taken by the same camera. The first image above is taken from the left then the other is on the right. 

Figure 3 The result of feature point detected on the stereo pair. 

The experiment includes the follow procedures. 1) The 62 conjugate points were used to calculate the parameters of the relative orientation of the stereo image pair. 2) Basing on the image space coordinate of the left image, the space coordinate of the object points corresponding to the selected six conjugate points were calculated using the result of the relative orientation and the forward intersection in photogrammetry. 3) The six object points were linked to 15 line segments during permutation and combination, and the distances of the 15 line segments were accurately measured as a real value. 4) To validate and assess the accuracy of the result of relative orientation, the distances of the 15 line segments were calculated using the space coordinate of the six object points, and compared with the measured true value. Then, the accuracy is assessed with the standard deviation.

Results and Analysis

For validating and assessing the accuracy of the result of relative orientation, the six object points (p1, p2, p3, p4, p5, p6) are selected and used to calculate the space coordinate basing on the image space coordinate of the left picture. The selected six object points are illustrated in Figure 4.

Figure 4 Six object points are selected for validating the accuracy of relative orientation. 

During the forward intersection, the space coordinates of the six object points was calculated with the result of relative orientation, the rotation matrix R, and translation matrix T. The space coordinates of the six object points represent in Table 1

Table 1 Three-dimensional coordinates of 6 object points (unit: m) 

To validate the correctness and assess the accuracy of the proposed new model, direct relative orientation with seven constraints, the distances of the six object points calculated with their space coordinate were compared with the corresponding measured distances, and the error rates were calculated and represented in Table 2. The first column shows the line segment composed of two points, such as (p1, p2), and the calculated distance and exact distance are in the second, third column, respectively.

Table 2 Error rate of the observed distance respect to the distance in real (unit: m) 

In addition, the curve of the error rates is calculated and shown in Figure 5. The blue square and curve represent the error rate of each line segment and the curve of error rates, respectively.

Figure 5 Error rate of the distance. 

From Table 2, it is evident that the minimum error of distances reaches 0.001 m and the maximum error is 0.0057 m. In the Figure 5, the range of error rates is between the -3% and +3%. The standard deviation of the distance accuracy is calculated and reaches 0.0031 m.

In the least squares adjustment, a wrong initial value will result in a very low precision of relative orientation, and even cause non-convergence or convergence to an error result. To overcome this problem, a reasonable initial value ofparameters (B_y B_Z, a₁, a₂ a₃...c₂, c₂, c₃) is calculated and acquired by direct relative orientation using a rough ^_BX. In the procedure, the value ^_BX can be an arbitrary value that is greater than zero. Then, the initial value of parameters in the relative orientation are used in the model of direct relative orientation with seven constraints to calculate further and adjust the parameters with the least squares adjustment, improving and ensuring the accuracy and stability of relative orientation.

Owing to the seven constraints, the error rate of distance used to assess the accuracy of relative orientation ranges for from -3% to +3%, and the standard deviation of the distance reaches 0.0031 m that describes the range error composed of two points. Therefore, the standard deviation of the point can be the half of distance error, 0.0015 m. Furthermore, the point is three dimensions; thus the standard deviation in each direction is 0.0005 m for the relative orientation. For a non-calibration and general camera sensor, the accuracy of relative orientation is excellent basing on the model of direct relative orientation with seven constraints, and the residual error may include the image distortion, match error of conjugate point, measurement error of image point, calculation error and random error. The residual error is from various factors and needed to eliminate with other methods to improve the accuracy of relative orientation further.

Conclusion

In this paper, a new relative orientation model, direct relative orientation with seven constraints is proposed and validated to improve the accuracy and stability of relative ordination and overcome the problems for the large oblique angle and translation and without the initial value. The constraints are derived from the inherent orthogonal property of rotation matrix and the vectors in space translation. Also, the procedure for solving direct relative orientation with seven constraints consists of the acquirement of initial value with direct relative orientation, the least square adjustment with seven constraints, and calculation of six relative orientation decompositions. The rough error is detected with data snooping techniques and used to analyze the residues of observations and the variance and covariance matrix of parameters.

During the experimental result and analysis, the model of direct relative orientation with seven can obtain a high accuracy than the conventional method in some cases, such as the large oblique angle and translation and without the initial value. In the cases, some result of the conventional method has very low accuracy or wholly wrong. However, the problems can overcome during the model of direct relative orientation with seven constraints. That means the proposed model can increase the applied field of relative orientation such as close range photography, low altitude oblique photography and 3D model reconstruction and measurement of the geological landslides with multiple images.