1. Introduction
The soils of Barranquilla, a city of Colombia, in South America, are mainly composed of layers of sand and gravel (Moreno, 2013). However, the western and southwestern part of the city (Figure 1) present extensive clay layers with swelling behavior (Geotecnología Ltda., 2006). In this part of Barranquilla, the overall type of construction is essentially residential housing. For this reason, the demographic density in this sector of the city is high. Since the mid-1970s, the western and southwestern zone of Barranquilla have presented large landslides and slopes instability problems (Figure 2) as a consequence of both anthropic and natural factors, and these phenomena have affected around two thousand low-income families (Guardo, 2000).
Some of the geotechnical problems in Barranquilla's western and southwestern zone are due to swell behavior of underlying clays (Geotecnología Ltda, 2006). Swelling of clays affects the structural stability of the overlying infrastructure; structural problems are often accentuated due to the topographical characteristics of the terrain, which is constituted by inclined slopes, leading to the collapse of structures, as illustrated in Figure 2. Studies developed to assess and understand the swelling behavior of these clays have been carried out by Geotecnología Ltda. (2006), and by Edgar Rodríguez (2014). The main goal of the work undertaken by Geotecnología Ltda. (2006) was to increase and improve the geological information regarding the western and southwestern part of the city. On the other hand, Rodríguez (2014) aimed to study the geological structure of clay materials in the zone. The results of Rodríguez (2014), Geotecnología Ltda. (2006), and other researchers revealed that most of the geotechnical problems of the area, are related to the water seepage through the clay layers. Geotecnología Ltda. (2006) explains these phenomena in detail in their work. They state that the upper soil layers in this zone are constituted by sands and gravels with high permeability, followed by Barranquilla's marine clays. During rainy seasons, the granular soils act as huge water retainers in the interface between these soils and the clays beneath. This accumulated water causes clays to swell and at the same time, it causes the loss of slope stability (Geotecnología Ltda., 2006). A typical soil profile for the study area is presented in Figure 3. Another important cause of landslides is that earth fills' inclination in some cases is greater than the clay's effective friction angle; for instance, some slopes have inclinations between 16° and 25° (Guardo, 2000), while the internal effective angle of friction for these materials ranges between 5° and 12° (Rodríguez, 2014).
Clays in Barranquilla's western and southwestern zone present prominent swelling behavior which is mainly produced by the montmorillonite clay mineral content (Feferbaum and Beltran, 1974). Soils with similar characteristics can be found in different zones around the world, for example in the United States, South-America, Africa, Australia, China and India (Murthy, 2011). Swell phenomena in clayey soils have been studied by Komornik and David (1969), Hensen and Smith (2002), Day (1991, 1992), among others. Several authors presented a variety of correlation equations to determine swell pressure of expansive clays, and examples of these equations are present in Erguler and Ulusay (2003), Sridharan and Gurtug (2004) and Phanikumar (2006). These investigations define the swell pressure value as a function of water content, Atterberg limits, dry unit weight and other parameters proposed by the authors, with laboratory tests designed by them. Erguler and Ulusay (2003), for instance, suggest the "maximum water content in 24 hours" and the "maximum water content in 72 hours" as predictive parameters, while Phanikumar (2006) introduces a parameter called Free Swell Index.
There is still a great necessity for civil and geotechnical engineering practice in the city to deepen the understanding of the mechanical properties of the soils in this zone of the city. In an effort to extend the knowledge about the mechanical behavior of clays in this part of Barranquilla, this technical note presents correlation equations to estimate swell pressure as a function of water content and Atterberg limits. Correlations found in this study could be useful in the study of expansive clays around with similar characteristics in different zones around the world.
Predictive equations presented in this technical note are based on the water contents and Atterberg limits of clays in Barranquilla's western and southwestern zone as explanatory variables. These properties were selected because they are widely used to develop swell pressure and swell index correlations in the literature, and at the same time, these measurements are perhaps the most prevalent in most geotechnical reports. The associated laboratory tests were performed following the procedures outlined by the Technical Specifications of INVIAS (Colombian National Institute of Roads): INV E-125-07 (corresponding to ASTM D 4318-00) to determine liquid limit, INV E-126-07 (corresponding to ASTM D 4318-00) to determine plastic limit, and INV E-122-07 (corresponding to ASTM D 2216-98) to determine water content.
2. Measurement of swell pressure
There are three standardized methodologies which determine swell pressure using laboratory testing (Sridharan, 2009): Swell - Load Method (Curve 1 on Figure 4), Swell Under Load Method (Curve 2 on Figure 4), and Constant Volume Method (Curve 3 on Figure 4). It should be mentioned that, as illustrated in Figure 4, each laboratory methodology to determine swell pressure yields different swell pressure values (Thompson et al., 2006; Kayabali and Demir, 2011).
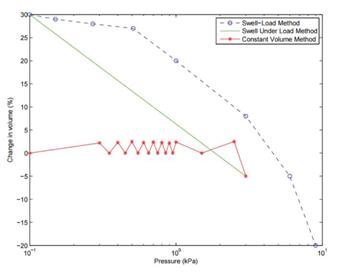
Figure 4 Typical Stress-Strain Curve in laboratory methodologies to determine Swell pressure. (after Sridharan et al., 2009)
In this study, the constant volume method was used to determine swell pressure values implemented to develop the correlations equations. The constant volume method, usually called strain controlled method, can be conducted by taking a specimen in a consolidation ring and applying a pressure equal to the result of the addition of the effective overburden pressure and the approximate anticipated surcharge caused by the foundation. Water is then added to the specimen to start swelling. As the specimen starts to swell, a small pressure increment is applied to prevent swelling. When the total stress causes specimen consolidation the swell pressure is attained. More details on the implemented constant volume method can be found in Das (2015).
3. Correlation equations.
Correlation equations presented in this section, are based on test results of Barranquilla's western and southwestern zone clays. Samples were obtained mainly from the area of Campo Alegre, because this zone is perhaps the most affected in the city as a consequence of landslides and swelling behavior of clays.
A total of 38 samples were used in this study. For each sample, water content, liquid limit, plastic limit, and void ratio were measured. Table 1 summarizes the maximum and minimum values for each soil property within the collected samples. The complete water content, liquid limit, plastic limit, plasticity index and void ratio information for each of the 38 samples is summarized in Appendix 1.
Logarithmic models ( y = a + b ln x ), and exponential models (ln y = a + bx) were used to model swell pressure (dependent variable) as a function of the selected properties. Only two models presented correlation coefficients and determination coefficients higher than 0.5; furthermore, only water content coefficients and models using water content as unique dependent variable were statistically significant. Correlation equations, determination coefficients ( R2 ) and correlation coefficients (r) of the developed models are presented in Table 2.
As can be seen in Table 2, statistically, the best fit and correlation equation to predict swell pressure is Equation 2. Table 3 summarizes goodness of fit parameters for the correlation equations. Figure 5(a) shows swell pressure-water content pairs measured for each specimen and swell pressure predictions using equations 1 and 2 from Table 2.
Among the different functional forms used to develop correlation equations between swell pressure and other soils properties, only a third equation (Equation 3) which incorporated plasticity index (PI) and water content as explanatory variables, presented high determination coefficient and correlation coefficient ( R2=0.86 and r=0.93 ):
however, the plasticity index was not statistically significant using a statistical significance of 0.05, having a P-value of 0.28 using a t-Student distribution (Table 3). Figure 5(b) shows the correlation from Equation 3 along the samples data; it results evident that the plasticity index does not have a major impact on swell pressure for the studied soil samples.
4. Discussion
A broader revision of swell pressure correlation equations can be found in Al-Rawas and Goosen (2006). Table 4 presents some relevant correlation equations and corresponding correlation coefficients reported by the authors.
Table 4 Correlation equations found in the literature.
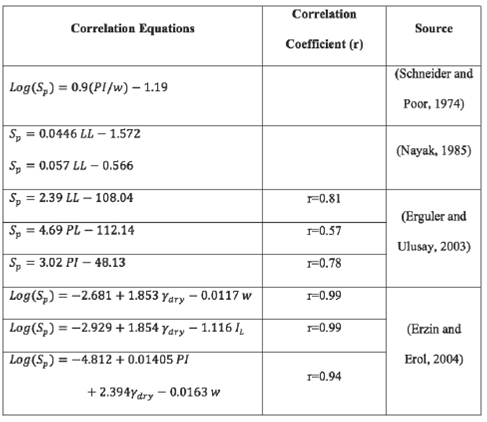
w is water content; PL is plastic Limit; LL is liquid limit; IL is liquidity index; γdry is dry unit weight.
Table 4, shows that for most of the presented correlation equations, correlation coefficient values are relatively high, which means that the equations could adequately predict the trend of the swell pressure measurements. Although correlation coefficients are high, it should be emphasized that the equations presented above be only valid in the measurement range of properties used to develop the equations. Another important fact is that the equations are only valid for the soils for which they were developed because swell properties vary among different clays. However, all the equations present similar trends among the various properties and swell pressure values. Similarly to the trend presented in this work, some of the proposed correlations yield a decrease in the logarithm of the swell pressure as a function of the water content. Erguler and Ulusay (2003), for instance, present the variation of swell pressure as a function of water content for soils samples collected at three different sites. In their work, swell pressure decays quickly as water content increases, reaching values of nearly 0 for water contents higher than 30%. Such behavior is similar to that shown in Figure 5 of this study.
5. Conclusions
This research presents correlation equations developed to estimate swell pressure of clays using laboratory tests performed on swelling clays in the city of Barranquilla, Colombia. Swell pressure values were estimated using the constant volume method. Estimated pressures reached values of more than 600 kPa for low levels of water content. Swell pressure values decayed quickly as water content increased, reaching values of nearly 0 for water contents higher than 40%. For the tested soils, it was found that swell pressure could be best modeled as an exponential function of the water content. While previous works by other authors use several additional soil properties (e.g., liquid limit, plastic limit, plasticity index or unit weight), it was found that for the studied soils adequate swell pressure estimates were obtained based solely on water content. Moreover, unlike previous works, it was found that Atterberg limits did not have statistical significance in the estimation of swell pressure for the studied samples.























