Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.9 no.17 Medellín Jan./June 2013
ARTÍCULO ORIGINAL
Estudio por primeros principios de las propiedades estructurales y electrónicas de la multicapa CrN/GaN
First-Principles Study of Structural and Electronic Properties of Chromium Nitride/Gallium Nitride Multilayer (CrN/GaN)
Ricardo Eulises Báez Cruz1, César Ortega López2 y Miguel J. Espitia R.3
1 Licenciado en Física, dfi.rbaez@pedagogica.edu.co, Universidad Pedagogica Nacional Bogota, Colombia.
2 Ph.D. en Física, cortegal@unicor.edu.co, Universidad de Córdoba, Montería, Colombia.
3 Ph.D. (C) en Física, mespitiar@udistrital.edu.co, Universidad Distrital Francisco José de Caldas, Bogotá, Colombia.
Recepción: 6-oct-2012, Aceptación: 31-ene-2013
Disponible en línea: 22-03-2013
PACS: 71.15.Mb, 71.15.Nc, 71.20.Nr
Resumen
En este trabajo realizamos cálculos de primeros principios para investigar las propiedades estructurales y electrónicas de la multicapa 1x1 CrN/GaN. Los cálculos se realizan en las fases zincblenda y wurtzita, debido a que este es el estado base del nitruro de cromo CrN y el nitruro de galio GaN, respectivamente. Sin embargo, se estudia la estabilidad de la multicapa en la fase NaCl, con el fin predecir posibles transiciones de fase. Encontramos que la fase más favorable para multicapa, es la hexagonal tipo wurtzita, con posibilidad de pasar a la fase NaCl mediante la aplicación de una presión externa. Nuestros cálculos nos permiten predecir que la presión de transición es  13,5 GPa. A partir de la densidad de estados encontramos que la multicapa posee un comportamiento metálico debido a la hibridación de los orbitales Cr-d y N-p que atraviesan el nivel de Fermi.
13,5 GPa. A partir de la densidad de estados encontramos que la multicapa posee un comportamiento metálico debido a la hibridación de los orbitales Cr-d y N-p que atraviesan el nivel de Fermi.
Palabras clave: Multicapa 1x1 CrN/GaN, DFT, propiedades estructurales, propiedades electrónicas.
Aspectos relevantes
• Este es un estudio teórico detallado de la multicapa CrN/GaN . • Se utiliza la teoría del funcional de la densidad. • Se calculan las propiedades estructurales y electrónicas. • Se encontró que la multicapa presenta propiedades magnéticas y comportamiento metálico
Abstract
In this work we perform first-principles calculations to investigate the structural and electronic properties of the 1x1 CrN/GaN multilayer. The calculations were executed in zincblende and wurtzite phase, since they are the ground states of chromium nitride CrN and gallium nitride GaN, respectively. However, we study the stability of the multilayer in the NaCl phase, in order to predict possible phase transitions. We found that the most favorable phase for the multilayer is the hexagonal wurtzite type, with possibility of passing to the NaCl phase by applying an external pressure. Our calculations indicate that the pressure of transition is  13,5 GPa. From the density of states, we found that the multilayer present a metallic behavior produced by the hybrid orbitals d-Cr and N-p that cross level Fermi.
13,5 GPa. From the density of states, we found that the multilayer present a metallic behavior produced by the hybrid orbitals d-Cr and N-p that cross level Fermi.
Key words: 1x1 CrN/GaN multilayer, DFT, structural properties, electronic properties.
1 Introducción
Los nitruros de metales de transición como el CrN han sido ampliamente estudiado teórica y experimentalmente, debido a sus excelentes propiedades mecánicas, físicas y químicas, tales como: alta dureza, elevado punto de fusión, alta resistencia al desgaste, a la corrosión y a la oxidación [1], [2], [3]. Se ha encontrado que nitruro de cromo CrN tiene un comportamiento metálico y que bajo condiciones normales de crecimiento cristalizan en la fase zincblenda [1], [4], [5], mientras que el nitruro de galio GaN es un semiconductor que cristaliza normalmente en wurtzita [6], [7]. Por otro lado, Vijay Rawat and Timothy Sands [8], [9] demostraron que es posible crecer multicapas de nitruros de metales de transición y nitruro de galio GaN, dado que, a pesar de la diferencia en la estructura cristalina NaCl del nitruro de titanio TiN y wurtzita del GaN crecieron multicapas de TiN/GaN usando la técnica Reactive Pulsed Laser Deposition (PLD).
El estudio de las multicapas basadas en nitruros de metales de transición y nitruro de galio GaN es de gran importancia actual, puesto que la combinación de las propiedades de los nitruros de mestales de transición, como el CrN, junto con el carácter semiconductor del GaN, le abren a las multicapas CrN/GaN un amplio espectro de aplicaciones, como por ejemplo: ser utilizadas en dispositivos de altas temperaturas, altas potencias, como recubrimientos duros y como un contacto metal/semiconductor, entre otras. Dada La posibilidad experimental de crecer multicapas de mestales de transición con el semiconductor nitruro de Galio GaN y el gran número de posibles aplicaciones de la multicapa CrN/GaN, es importante realizar estudios teóricos que brinden información sobre la estabilidad estructural, las propiedades estructurales y electrónicas de ésta multicapa. Por esta razón, en este trabajo estudiamos en el marco de la teoría del funcional de la densidad DFT, las propiedades estructurales y electrónica de la multicapa 1x1 CrN/GaN. En particular, estamos interesados en determinar la estabilidad relativa de la multicapa CrN/GaN, inicialmente estudiamos la estabilidad de la multicapa en las fases zincblenda y wurtzita debido a que este es el estado base de los compuestos binarios CrN y GaN, respectivamente. Adicionalmente, estudiamos la estabilidad de la multicapa en la fase NaCl. Encontramos que la fase más favorable para la multicapa es la modelada en la estructura wurtzita. A 13,5 GPa, nuestros cálculos predicen la posibilidad de una transición de fase de la estructura wurtzita a la estructura NaCl.
2 Detalles de Cálculo
Los cálculos se realizan dentro del marco de la Teoría del Funcional Densidad (DFT) y usando Ondas Planas Aumentadas y linealizadasPotencial Completo (FP-LAPW) implementado en el paquete WIEN2k [10]. Los efectos de correlación e intercambio de los electrones se tratan usando la aproximación de Gradiente Generalizado (GGA) de Perdew, Burke y Ernzerhof (PBE) [11]. En el método LAPW la celda se divide en dos tipos de regiones, las esferas atómicas centradas en los sitios nucleares y la región intersticial entre las esferas no superpuestas. Dentro de las esferas atómicas las funciones de ondas se reemplazan por funciones atómicas, mientras que en la región intersticial, la función se expande en ondas planas. La densidad de carga y los potenciales se expanden en armónicos esféricos hasta lmax = 10 dentro de las esferas atómicas y la función de onda en la región intersticial se expande en ondas planas con un parámetro de corte Kmax = 8/Rmt donde Rmt es el radio más pequeño de la esfera atómica en la celda unitaria y Kmax es la magnitud del vector k más grande de la red recíproca. Para asegurar convergencia en la integración de la primera zona de Brillouin se utilizaron 1600 puntos, lo que corresponde a 140 puntos k en la parte irreducible de la primera zona de Brillouin para la fase NaCl, 126 puntos k en la parte irreducible de la primera zona de Brillouin para la fase Zincblenda y 144 puntos k en la parte irreducible de la primera zona de Brillouin para la fase wurtzita. Las integrales sobre la zona de Brillouin se resuelven usando la aproximación especial puntos k de Monkhorst-Pack. La autoconsistencia se logra exigiendo que la convergencia de la energía total sea menor que 10-4 Ry. Para la expansión del potencial en la región intersticial, se considera Gmax = 12. Los radios Muffin-tin fueron de 1.6 bohr para el N, 1.95 bohr para el Ga y 1.85 para el Cr. Los cálculos se realizan teniendo en cuenta la polarización de espín, debido a la presencia del átomo Cr.
Para determinar tanto la fase de cristalización más estable a una presión y temperatura finita, como una posible transición de fase producida por presión, utilizamos la energía libre de Gibb G = E + PV + TS. Adicionalmente, dado que se han reportado transiciones de fase estructural para los nitruros de metales de transición y las transiciones fase de la estructura NaCl  wurtzita son independientes de la temperatura [12], se puede despreciar el último término de la energía de Gibb y tomando la entalpía, la energía libre de Gibb se simplifica a: H = E + PV [12], [13], [14]. Usamos esta ecuación para las tres estructuras cristalinas consideradas en este trabajo, sin embargo, no podemos excluir la posible existencia de otras estructuras estables o metaestables para la multicapa 1x1 CrN/GaN.
wurtzita son independientes de la temperatura [12], se puede despreciar el último término de la energía de Gibb y tomando la entalpía, la energía libre de Gibb se simplifica a: H = E + PV [12], [13], [14]. Usamos esta ecuación para las tres estructuras cristalinas consideradas en este trabajo, sin embargo, no podemos excluir la posible existencia de otras estructuras estables o metaestables para la multicapa 1x1 CrN/GaN.
Para obtener la constante de red, el volumen mínimo, el módulo de volumen y la energía de cohesión de cada estructura estudiada, los datos calculados fueron ajustados a la ecuación de estado de Murnaghan (1).

Donde Boes el modulo de volumen, su primera derivada es B'o , Vo es volumen de equilibrio de la celda y Eo es la energía de cohesión.
3 Resultados y Análisis
3.1 Propiedades estructurales
Encontramos que la multicapa 1x1 CrN/GaN modelada en la fase NaCl mediante la intercalación de una capa de GaN y una capa de CrN a lo largo de eje z, cristaliza en una estructura tetragonal con grupo espacial 123 (P4/mmm), mientras que la multicapa modelada en la fase wurtzita cristaliza en una estructura perteneciente al grupo espacial 156 (P3m1) y la modelada en la fase zincblenda cristaliza en la estructura perteneciente al grupo espacial 122 (I - 42d). La constante de red de la multicapa, los valores c/a, el módulo de volumen (Bo), el volumen mínimo (Vo) y la energía mínima (Eo) (por fórmula unidad) de la multicapa 1x1 CrN/GaN calculadas en las estructuras wurtzita, zincblenda y NaCl son mostrados en la Tabla 1.
Se observa que el valor más pequeño del mínimo de energía ocurre en la fase wurtzita, por tanto, la estructura más favorable de cristalización para la multicapa 1x1 CrN/GaN es la hexagonal tipo wurtzita. Los valores de los módulos de volumen son altos, lo que confirma que este compuesto posee alta dureza, lo que los hace atractivo para posibles aplicaciones en altas temperaturas y en recubrimientos duros.
La Figura 1 muestra las curvas de energía total como una función del volumen y ajustadas a la ecuación de estado de Murnaghan Ecuación (1) para cada una de las tres fases estructurales consideradas en el presente estudio. Las energías y volúmenes están dados por fórmula unidad de la multicapa CrN/GaN.
Hemos tomado como cero la suma de las energías de los átomos neutros del Cr, Ga y N aislados. Por consiguiente, el valor absoluto del mínimo de la energía de cada curva, es la energía de cohesión de la multicapa 1x1-CrN/GaN en la fase correspondiente. En la Figura 1 se observa que cada estructura considerada es metaestable, ya que existe un mínimo de energía en la curva correspondiente. La fase estructural más estable calculada en el estado base (T = 0°K) es la hexagonal tipo wurtzita, debido a que su valor mínimo de energía es el más bajo de todas las curvas examinadas. Lo que confirma el resultado mostrado en la Tabla 1.
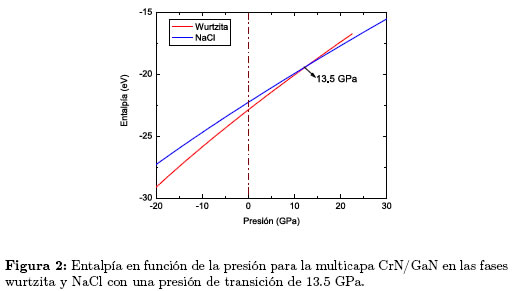
En la Figura 1 se observa que la curva correspondiente a la fase más estable, hexagonal tipo wurtzita, se cruza con la curva de la estructura NaCl de menor volumen de equilibrio, lo que indica una transición de fase de la multicapa, de la fase wurtzita a la fase NaCl. La energía mínima (Eo) de la multicapa CrN/GaN en la fase NaCl es 0,2164 eV/(fórmula unidad) más alta que la correspondiente a la fase wurtzita; por lo tanto, la transición de fase en la multicapa se debe inducir aplicando una presión externa. Con el fin de describir la transición de fase, calculamos la entalpía en función de la presión para cada estructura. Al sobreponer las rectas de entalpía en función de la presión, como muestra la Figura 2, obtenemos un valor de PT = 13,5 GPa para la presión de transición.
Nótese que antes de la transición (p <PT) el valor más bajo de la entalpía corresponde a la fase wurtzita, indicando estabilidad relativa de esta fase en ese rango de presiones; mientras que, después de la transición (p >PT) la fase NaCl tiene la entalpía más baja, confirmando su estabilidad en esta región del diagrama de fase. Durante la transición de fase se presenta una reducción del 18, 96 % del volumen, cuando pasa de 46,39 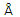 3 en la fase wurtzita a 37, 59
3 en la fase wurtzita a 37, 59 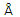 3 en la fase NaCl. También encontramos que el módulo de volumen de la multicapa CrN/GaN en la fase NaCl aumenta significativamente respecto al módulo de volumen en la fase wurtzita, lo que indica que la cristalización de la multicapa 1x1 CrN/GaN en la fase NaCl da como resultado un material mucho más rígido que en la fase wurtzita.
3 en la fase NaCl. También encontramos que el módulo de volumen de la multicapa CrN/GaN en la fase NaCl aumenta significativamente respecto al módulo de volumen en la fase wurtzita, lo que indica que la cristalización de la multicapa 1x1 CrN/GaN en la fase NaCl da como resultado un material mucho más rígido que en la fase wurtzita.
3.2 Propiedades electrónicas
La Figura 3 muestra la densidad de estados total y parcial en la fase más favorable calculada en este trabajo.
La Figura 4 muestra la densidad de estados total y parcial en la fase NaCl calculada en este trabajo
Encontramos que, tanto en la fase wurtzita como en la NaCl la multicapa 1x1 CrN/GaN presenta un comportamiento metálico, en oposición al GaN tipo wurtzita que tiene un comportamiento semiconductor (gap experimental  3.4 eV). El comportamiento metálico de la multicapa CrN/GaN, está determinado principalmente por los electrones Cr-d y en una mínima proporción por los electrones N-p. Por otro lado, el acoplamiento entre los estados metálicos Cr-d y los estados no metálicos N-p resultan en un fuerte enlace covalente responsable de la alta dureza del compuesto [15].
3.4 eV). El comportamiento metálico de la multicapa CrN/GaN, está determinado principalmente por los electrones Cr-d y en una mínima proporción por los electrones N-p. Por otro lado, el acoplamiento entre los estados metálicos Cr-d y los estados no metálicos N-p resultan en un fuerte enlace covalente responsable de la alta dureza del compuesto [15].
En la fase wurtzita la banda de valencia está divida en tres regiones, la primera entre  - 15 eV y
- 15 eV y  -13 eV está gobernada principalmente por los estados Ga-d con una pequeña contribución de los estados N-s. La región entre
-13 eV está gobernada principalmente por los estados Ga-d con una pequeña contribución de los estados N-s. La región entre  -7 eV y
-7 eV y  - 2.5 eV se compone por los estados híbridos Np y Cr-d en la misma proporción. La región entre
- 2.5 eV se compone por los estados híbridos Np y Cr-d en la misma proporción. La región entre  -2.5 eV y el nivel de Fermi se compone principalmente por los estados Cr-d con una pequeña contribución de los electrones N-p. La multicapa presenta propiedades magnéticas, siendo el momento magnético por celda de 6,0 magnetones de Bohr, además se observa mayor localización de los estados, indicada por los picos cercanos al nivel de Fermi y constituidos básicamente por los estados Cr-d.
-2.5 eV y el nivel de Fermi se compone principalmente por los estados Cr-d con una pequeña contribución de los electrones N-p. La multicapa presenta propiedades magnéticas, siendo el momento magnético por celda de 6,0 magnetones de Bohr, además se observa mayor localización de los estados, indicada por los picos cercanos al nivel de Fermi y constituidos básicamente por los estados Cr-d.
En la fase NaCl Figura 4, la banda de valencia presenta una región profunda alrededor de los  -15 eV, constituida principalmente por el estado Ga-d, la región comprendida entre
-15 eV, constituida principalmente por el estado Ga-d, la región comprendida entre  -9 eV y el nivel de fermi, se compone principalmente por los electrones Cr-d y en menor contribución por los electrones N-p. Entre
-9 eV y el nivel de fermi, se compone principalmente por los electrones Cr-d y en menor contribución por los electrones N-p. Entre  -2 eV y el nivel de Fermi se observa mayor localización de los estados, indicada por los picos cercanos al nivel de Fermi y constituidos básicamente por los estados Cr-d. La multicapa presenta un comportamiento magnético, con un momento magnético por celda de 2,96 magnetones de Bohr.
-2 eV y el nivel de Fermi se observa mayor localización de los estados, indicada por los picos cercanos al nivel de Fermi y constituidos básicamente por los estados Cr-d. La multicapa presenta un comportamiento magnético, con un momento magnético por celda de 2,96 magnetones de Bohr.
Tanto en la fase wurtzita como NaCl, la multicapa presenta propiedades magnéticas, debido principalmente a los estados Cr-d. Un resultado teórico similar fue encontrado en closter de GaN dopados con Cr [16].
4 Conclusiones
Reportamos cálculos de primeros principios para determinar las propiedades estructurales y electrónicas de las multicapas 1x1 de CrN/GaN. Encontramos que los valores de los módulos de volumen son altos, lo cual significa que la multicapa es muy rígida, haciéndola atractiva para posibles aplicaciones a altas temperaturas, en recubrimientos duros, como contacto metal semiconductor, entre otras. A partir de la densidad de estados, encontramos que la multicapa tanto en la fase wurtzita como NaCl presenta comportamiento metálico, debido a los orbitales Cr-d y N-p que atraviesan el nivel de Fermi. Encontramos que la multicapa 1x1-CrN/GaN posee propiedades magnéticas debidas a la polarización de los espines de los electrones pertenecientes a los orbitales d-Cr, con momento magnético por celda de 2,96 magnetones de Bohr en la fase NaCl y de 6,0 magnetones de Bohr en la fase wurtzita, lo que le abre a la multicapa la posibilidad de aplicaciones en espintrónica.
Referencias
[1] A. Zaoui, S. Kacimi, B. Bouhafs, and A. Roula, ''First-principles study of bonding mechanisms in the series of Ti, V, Cr, Mo, and their carbides and nitrides,'' Physica B: Condensed Matter, vol. 358, no. 1-4, pp. 63-71, 2005. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0921452604012724 164
[2] Z. Dridi, B. Bouhafs, P. Ruterana, and H. Aourag, ''First-principles calculations of vacancy effects on structural and electronic properties of TiCx and TiNx,'' J. Phys.: Condens. Matter, no. 14, pp. 10 237-10 249, 2002. [ Links ] 164
[3] I. Pollini, A. Mosser, and J. C. Parlebas, ''Electronic, spectroscopic and elastic properties of early transition metal compounds,'' Physics Reports, vol. 355, no. 1, pp. 1-72, 2001. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0370157301000187 164
[4] C. Kral, W. Lengauer, D. Rafaja, and P. Ettmayer, ''Critical review on the elastic properties of transition metal carbides, nitrides and carbonitrides,'' Journal of Alloys and Compounds, vol. 265, no. 1-2, pp. 215-233, 1998. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0925838897002971 164
[5] G. Casiano, W. López, and J. Rodríguez, ''Estabilidad Relativa del Compuesto CrN,'' Revista de la Sociedad Colombiana de Física, vol. 41, no. 3, pp. 580-583, 2009. [ Links ] 164
[6] O. Arbouche, B. Belgoumène, B. Soudini, and M. Driz, ''First principles study of the relative stability and the electronic properties of GaN,'' Computational Materials Science, vol. 47, no. 2, pp. 432-438, 2009. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0927025609003516 164
[7] J.-M. Wagner and F. Bechstedt, ''Properties of strained wurtzite GaN and AlN: Ab initio studies,'' Phys. Rev. B, vol. 66, no. 11, p. 115202, Sep. 2002. [ Links ] [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevB.66.115202 164
[8] V. Rawat and T. Sands, ''Growth of TiN/GaN metal/semiconductor multilayers by reactive pulsed laser deposition,'' Journal of Applied Physics, vol. 100, no. 6, p. 64901, 2006. [ Links ] [Online]. Available: http://link.aip.org/link/?JAP/100/064901/1 164
[9] V. Rawat, D. N. Zakharov, E. A. Stach, and T. D. Sands, ''Pseudomorphic stabilization of rocksalt GaN in TiN/GaN multilayers and superlattices,'' Phys. Rev. B, vol. 80, no. 2, p. 24114, Jul. 2009. [ Links ] [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevB.80.024114 165
[10] K. Schwarz, ''DFT calculations of solids with LAPW and WIEN2k,'' Journal of Solid State Chemistry, vol. 176, no. 2, pp. 319-328, 2003. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0022459603002135 165
[11] J. P. Perdew, K. Burke, and M. Ernzerhof, ''Generalized Gradient Approximation Made Simple,'' Phys. Rev. Lett., vol. 77, no. 18, pp. 3865-3868, Oct. 1996. [ Links ] [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevLett.77.3865 166
[12] R. González, W. López, and J. A. R. M., ''First-principles calculations of structural properties of GaN : V,'' Solid State Communications, vol. 144, no. 3-4, pp. 109-113, 2007. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0038109807006084 166 [ Links ]
[13] L. Mancera, J. A. Rodríguez, and N. Takeuchi, ''Theoretical study of the stability of wurtzite, zinc-blende, NaCl and CsCl phases in group IIIB and IIIA nitrides,'' physica status solidi (b), vol. 241, no. 10, pp. 2424-2428, 2004. [ Links ] [Online]. Available: http://dx.doi.org/10.1002/pssb.200404910 166
[14] N. Takeuchi, ''First-principles calculations of the ground-state properties and stability of ScN,'' Phys. Rev. B, vol. 65, no. 4, p. 45204, 2002. [ Links ] [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevB.65.045204 166
[15] S.-H. Jhi, J. Ihm, S. G. Louie, and M. L. Cohen, ''Electronic mechanism of hardness enhancement in transition-metal carbonitrides,'' Nature, vol. 399, no. 6732, pp. 132-134, 1999. [ Links ] [Online]. Available: http://dx.doi.org/10.1038/20148 171
[16] J. Rufinus, ''Magnetic properties of M-doped (M=Ti, V, or Cr) GaN clusters,'' Journal of Magnetism and Magnetic Materials, vol. 310, no. 2, Part 2, pp. 1666-1668, 2007. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0304885306017239 172