1. Introducción
El proceso de localización de locales comerciales algunas veces se lleva a cabo de manera intuitiva. Este aspecto se debe valorar de la mejor manera posible, ya que es un factor que puede generar ventajas competitivas (Hualpa-Zúñiga y Suárez-Roldán, 2013). Además, difícilmente esta decisión se puede modificar en el corto plazo. La elección de una buena localización juega un papel crucial en las industrias minorista y de servicios, ya que es importante para atraer a más clientes e impactar, de manera sustancial, en la participación de mercado (Chen y Tsai, 2016). Por esta razón se puede afirmar que se trata de un problema de decisión estratégicamente importante.
Yıldız y Tüysüz (2018), por su parte, señalan cuatro teorías que se desarrollaron con relación a la selección de la localización de locales minoristas: la teoría de lugar central, la teoría de interacción espacial, la teoría de renta de oferta y el principio de diferenciación mínima, así como otras técnicas disponibles. Sevtsuk (2014) menciona que existen modelos matemáticos que permiten predecir ubicaciones potenciales de tiendas minoristas, sin embargo, este problema de localización puede evaluarse según varios criterios. En razón a lo anterior, el objetivo de este trabajo es desarrollar una metodología basada en técnicas de decisión multicriterio para la selección de la localización de tiendas minoristas mediante la combinación entre proceso de jerarquía analítica AHP difuso o FAHP, por sus siglas en inglés, y la técnica para el orden de preferencia por similitud a la solución ideal o TOPSIS, por sus iniciales en inglés. Estas herramientas, en razón a su lógica y estructura metodológica, facilitan este proceso de toma de decisiones empresariales. Los métodos de decisión multicriterio ayudan a los responsables de la toma de decisiones a resolver problemas de decisión complejos que involucran criterios contradictorios, los cuales son difícilmente cuantificables de una manera sistemática y consistente (Sennaroglu y Celebi, 2018).
El artículo se desarrolla de la siguiente manera. En la segunda sección se presentan las técnicas de decisión multicriterio y sus aplicaciones. La metodología propuesta se desarrolla en la tercera sección y, a continuación, en la cuarta sección se presenta un estudio de caso aplicado para la selección de localización de una tienda minorista en Barranquilla. En la quinta sección se analizan los resultados y se finaliza con la presentación de las conclusiones.
2. Revisión de la literatura
El proceso de jerarquía analítica o AHP, por sus siglas en inglés, desarrollado por Saaty (1980), ha sido extensamente utilizado en la toma de decisiones multicriterio. Este método emplea datos cuantitativos y cualitativos, los cuales se traducen en números. El AHP es una teoría de la medición mediante comparaciones por pares. El método se usa con el fin de comparar alternativas y determinar su importancia entre sí, mediante un proceso sistemático y jerárquico (Bhushan y Rai, 2007; Saaty, 2008). Las comparaciones se realizan mediante una escala de juicios absolutos que representa la medida de dominación de un elemento sobre otro con respecto a un atributo dado. Lidiar con juicios inciertos a fin de expresar la importancia de los criterios indica la posibilidad de usar conjuntos difusos o números borrosos, lo que incorpora la vaguedad del pensamiento humano. Dado que es difícil mediante preferencias cualitativas realizar las estimaciones, se asociará un grado de incertidumbre con algunos o todos los pares de valores de comparación en un problema de AHP. Con el fin de incorporar la falta de claridad en la toma de decisiones de múltiples criterios muchos autores han utilizado el proceso de jerarquía analítica difuso o FAHP, tal como lo indican Carlsson y Fullér (1996). En el método FAHP se reemplaza la escala tradicional por una escala numérica triangular difusa, con lo cual se logra un manejo más eficaz de la imprecisión de los juicios lingüísticos de los responsables de la toma de decisiones, y se recibe así una mejor aceptación por parte de los investigadores con relación a la del método original (Santis, Golliat y Aguiar, 2017).
El proceso de jerarquía analítica o AHP es una de las herramientas de análisis multicriterio ampliamente utilizadas en la toma de decisiones para modelar problemas no estructurados en diferentes áreas, como, por ejemplo, en ciencias políticas, económicas, sociales y de gestión. Muchos estudios han aplicado AHP y FAHP en diferentes situaciones y problemas. Así, por ejemplo, el de Dožić, Lutovac y Kalić (2018) en la selección del tipo de aviones para pasajeros; el de Jayawickrama, Kulatunga y Mathavan (2017) con el fin de evaluar la sostenibilidad de una planta de fabricación; el de Gürcan, Beyca, Arslan y Eldemir (2016) en la selección de proveedores; o el de Mosadeghi, Warnken, Tomlinson y Mirfenderesk (2015) que compara los métodos AHP y FAHP en la definición de la extensión de las zonas de uso de la tierra en un escenario de planificación urbana a gran escala. En aplicaciones de localización se destaca el trabajo de Asakereh, Soleymani y Sheikhdavoodi (2017) para ubicación de granjas solares; el de Chauhan y Singh (2016) en la localización de depósitos para residuos sanitarios; y el de Hong y Xiaohua (2011) en la localización de centros logísticos de emergencia.
La técnica para el orden de preferencia por similitud a la solución ideal o TOPSIS, desarrollado por Hwang y Yoon en 1981, es un método simple de clasificación en la concepción y la aplicación. El método estándar TOPSIS intenta elegir alternativas que presenten, de forma simultánea, la distancia más corta desde la solución ideal positiva y la distancia más alejada de la solución ideal negativa. La solución ideal positiva maximiza los criterios de beneficio y minimiza los criterios de costo, mientras que la solución ideal negativa maximiza los criterios de costo y minimiza los criterios de beneficio (Behzadian, Otaghsara, Yazdani e Ignatius, 2012). Al igual que el AHP, la técnica TOPSIS se ha utilizado para diferentes aplicaciones: Jumaah et al. (2018) la utilizaron en la evaluación de los modos de operación de sistemas de posicionamiento global, Walczak y Rutkowska (2017) en la clasificación de proyectos en un presupuesto participativo, y Senouci, Mushtaq, Hoceini y Mellouk (2016) en la selección de interfaces de redes de comunicaciones móviles inalámbricas.
En la aplicación combinada de AHP-TOPSIS se pueden mencionar los trabajos de Hsieh et al. (2018) dirigidos a identificar factores de error humanos en departamentos de emergencia; los de Zhao et al. (2018) para la selección de la ubicación de los centros de distribución; los de Kazazi, Akbari, Jabbari y Asefi (2018) a fin de determinar la ubicación de estacionamientos en consideración a múltiples criterios económicos, sociales y ambientales; los de Alizadeh, Rad y Bazzazi (2016) para seleccionar un método de procesamiento de alúmina; y los de Beikkhakhian, Javanmardi, Karbasian y Khayambashi (2015) utilizados en la evaluación de proveedores.
3. Metodología
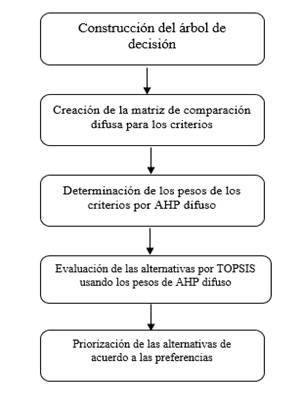
La metodología utilizada en este artículo para la selección de la localización de un local comercial es una combinación de FAHP orientada a definir la ponderación de la jerarquía de criterios y el método TOPSIS a fin de determinar el mejor orden de las alternativas. A pesar de que la toma de decisiones se puede realizar mediante FAHP, la integración con otras herramientas de decisión multicriterio mejora el proceso de decisión (Prakash y Barua, 2015). A continuación, se detallan los pasos a seguir.
El proceso de jerarquía analítica difuso o FAHP se utiliza para proporcionar la importancia de los criterios en la selección de localización. Los pasos son:
Paso 1. Identificación de los criterios para la selección de la localización.
Paso 2. Creación de la matriz difusa de comparación de criterios.
Paso 3. Determinación de los pesos o ponderación de cada criterio según Büyüközkan, Kahraman y Ruan (2004).
TOPSIS se utiliza con la finalidad de realizar una clasificación o ranquin de las alternativas de localización en la que se utilizan los valores normalizados de los elementos en la matriz de decisión (Hwang y Yoon, 1981). Los pasos son:
Paso 1. Elaborar una matriz de desempeño con el fin de evaluar cada alternativa de localización con respecto a cada uno de los criterios que se consideran.
Paso 2. Construir la matriz ponderada normalizada multiplicando los elementos por las ponderaciones de los criterios determinadas con AHP difuso.
Paso 3. Determinar las soluciones ideal positiva e ideal negativa.
Paso 4. Calcular la distancia de cada alternativa a la solución ideal positiva y de la solución ideal negativa.
Paso 5. Calcular el coeficiente de proximidad o Ri.
Paso 6. Ordenar las alternativas utilizando los valores de Ri. Cuanto mayor sea la puntuación mejor será la alternativa.
4. Estudio de caso: aplicación del método propuesto para la selección de localización de locales comerciales
El caso de aplicación se desarrolla en Barranquilla, Colombia, con el propósito de identificar la mejor ubicación de una tienda de ropa deportiva en un centro comercial de la ciudad. Inicialmente, se conformó un grupo de expertos para la identificación de los centros comerciales y de los criterios de selección de localización.
Los centros comerciales que se han propuesto para ubicar la tienda son los siguientes: CC Americano-A1, CC Buenavista-A2, CC Miramar-A3, CC Único-A4, CC Portal del Prado-A5 y CC Viva-A6. Los criterios de selección son: infraestructura del centro comercial-Crit.1, costo de arrendamiento-Crit.2, accesibilidad de clientes-Crit.3 y potencial comercial-Crit.4.
4.1. Determinación de los pesos de los criterios utilizando AHP difuso
Una vez se determinan los criterios, el siguiente paso se dedica a obtener los pesos de prioridad de cada atributo, es decir, los criterios. Las comparaciones por pares se realizan en términos lingüísticos y sus números difusos triangulares, tal como se define en la tabla 1. Luego, se inserta la información requerida para el análisis y se obtiene la matriz difusa de comparación de los criterios principales con los pesos calculados que se presentan en la tabla 2.
Tabla 1 Escala de comparaciones por pares
| Escala lingüística | Escala numérica | Escala triangular difusa |
|---|---|---|
| Igualmente importante | 1 | (1,1,2) |
| Moderadamente más importante | 3 | (2,3,4) |
| Fuertemente más importante | 5 | (4,5,6) |
| Absolutamente más importante | 7 | (6,7,8) |
| Muy fuertemente más importante | 9 | (8,9,9) |
| Valores intermedios | 2, 4, 6, 8 | (1,2,3) (3,4,5) (5,6,7) (7,8,9) |
Fuente. Guerrero, Marín y Gómez 2016.
Tabla 2 Matriz de comparaciones difusa
| C1 | C2 | C3 | C4 | ||||||||||
| C1 | 1 | 1 | 1 | 1/3 | 1/2 | 1 | 2 | 3 | 4 | 1/5 | 1/4 | 1/3 | |
| C2 | 1 | 2 | 3 | 1 | 1 | 1 | 1 | 2 | 3 | 1/3 | 1/2 | 1 | |
| C3 | 1/4 | 1/3 | 1/2 | 1/3 | 1/2 | 1 | 1 | 1 | 1 | 1/6 | 1/5 | 1/4 | |
| C4 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 1 | 1 | |
Fuente. Elaboración propia.
Se procede a determinar los pesos de cada criterio de acuerdo con lo que plantean Büyüközkan et al. (2004), se calcula inicialmente el grado sintético difuso (Tabla 3), posteriormente se comparan los números difusos de la matriz de criterios (Tabla 4) y, por último, se realiza la normalización a fin de obtener el vector de peso de los criterios de dicha matriz (Tabla 5).
Tabla 3 Grado sintético difuso
| C1 | 0,110 | 0,196 | 0,360 |
| C2 | 0,104 | 0,226 | 0,454 |
| C3 | 0,055 | 0,084 | 0,156 |
| C4 | 0,281 | 0,494 | 0,851 |
Fuente. Elaboración propia.
Tabla 4 Comparación de números difusos
| C1-C2 | 0,89 | C2-C1 | 1 | C3-C1 | 0,29 | C4-C1 | 1 |
| C1-C3 | 1 | C2-C3 | 1 | C3-C2 | 0,27 | C4-C2 | 1 |
| C1-C4 | 0,21 | C2-C4 | 0,39 | C3-C4 | 0 | C4-C3 | 1 |
Fuente. Elaboración propia.
Tabla 5 Peso normalizado de criterios
| C1 | 0,1119 |
| C2 | 0,2103 |
| C3 | 0,1432 |
| C4 | 0,5346 |
Fuente. Elaboración propia.
4.2. Aplicación de TOPSIS en el ranquin de ubicaciones alternativas
Se procede a la aplicación del método TOPSIS para la selección de la mejor localización. Los pesos de cada criterio calculados por FAHP se usan como valores de entrada para el TOPSIS. A fin de identificar cada alternativa y su respectiva evaluación, el grupo de expertos consideró diferentes factores que satisfacen todos los criterios (Tabla 6).
Tabla 6 Matriz de calificación de las alternativas
| PESO | A1 | A2 | A3 | A4 | A5 | A6 | |
| C1 | 0,1119 | 4 | 7 | 2 | 5 | 4 | 8 |
| C2 | 0,2103 | 8 | 4 | 7 | 9 | 6 | 3 |
| C3 | 0,1432 | 3 | 8 | 2 | 4 | 5 | 6 |
| C4 | 0,5346 | 6 | 7 | 5 | 7 | 6 | 8 |
Fuente. Elaboración propia.
De acuerdo con Hanine, Boutkhoum, Tikniouine y Agouti (2016), el segundo paso en la técnica es la normalización de la matriz de calificaciones agregadas, tal como se ilustra en la tabla 7. A continuación, se determinan las soluciones ideales positivas y negativas -d+, d--, se calcula la distancia euclidiana de cada alternativa a las soluciones ideales y a partir de estos valores la proximidad relativa Ri; por último, se ordenan en sentido decreciente las alternativas (Tabla 8).
Tabla 7 Matriz de calificación normalizada
| A1 | A2 | A3 | A4 | A5 | A6 | |
| C1 | 0,0339 | 0,05936 | 0,017 | 0,0424 | 0,0339 | 0,0678 |
| C2 | 0,1054 | 0,05269 | 0,0922 | 0,11854 | 0,079 | 0,0395 |
| C3 | 0,0346 | 0,09229 | 0,0231 | 0,04615 | 0,0577 | 0,0692 |
| C4 | 0,1993 | 0,23255 | 0,1661 | 0,23255 | 0,1993 | 0,2658 |
Fuente. Elaboración propia.
5. Resultados y discusión
Tal como se muestra en la tabla 5, el criterio valorado con la mayor importancia es potencial comercial con una ponderación del 53,46 %, seguido por costos de arrendamiento con un 21,03 %; accesibilidad de clientes con un 14,32 %; y, finalmente, infraestructura física con el 11,19 %. Al observar las calificaciones de las alternativas en el criterio potencial comercial no hay mucha diferenciación, lo cual hace difícil la decisión; por tanto, la consideración de los otros criterios resultó definitiva para la selección final. Nótese que las alternativas A2 y A5 están por encima en el ordenamiento final sobre A6, que es la que tiene mejor calificación en el criterio de mayor ponderación.
Se realizó un análisis de sensibilidad con el fin de determinar el impacto de la apreciación dada por los tomadores de decisiones sobre la selección de la mejor ubicación para un almacén de ropa deportiva. En el análisis de sensibilidad se intercambian los pesos de dos criterios mientras que los otros dos permanecen constantes. Cada combinación se declara como un caso (Tabla 9).
Tabla 9 Análisis de sensibilidad
| A1 | A2 | A3 | A4 | A5 | A6 | Ranquin | |
| Caso 1 -pesos orig.- | 0,3301 | 0,6607 | 0,4471 | 0,2860 | 0,5371 | 0,5074 | A2-A5-A6-A3-A1-A4 |
| Caso 2 | 0,3796 | 0,5758 | 0,4884 | 0,2822 | 0,5775 | 0,4548 | A2-A5-A3-A6-A1-A5 |
| Caso 3 | 0,3566 | 0,6022 | 0,4873 | 0,2782 | 0,5498 | 0,4893 | A2-A5-A6-A3-A1-A4 |
| Caso 4 | 0,3639 | 0,4828 | 0,5180 | 0,2794 | 0,5599 | 0,4601 | A5-A3-A2-A6-A1-A4 |
| Caso 5 | 0,2992 | 0,7180 | 0,3893 | 0,3030 | 0,5348 | 0,5145 | A2-A5-A6-A3-A4-A1 |
| Caso 6 | 0,2097 | 0,8115 | 0,2275 | 0,2889 | 0,4017 | 0,7099 | A2-A6-A5-A4-A3-A1 |
| Caso 7 | 0,1739 | 0,9067 | 0,1059 | 0,3276 | 0,4973 | 0,6568 | A2-A6-A5-A4-A1-A3 |
| Caso 8 -pesos iguales- | 0,2297 | 0,6962 | 0,3227 | 0,3074 | 0,4963 | 0,5599 | A2-16-15-A3-A4-A1 |
Fuente. Elaboración propia.
Adicionalmente, se expresó la matriz de comparación difusa de criterios como una matriz de números reales, lo cual se realizó para calcular los pesos de los criterios con la metodología AHP. A continuación, se muestran la matriz y las ponderaciones de cada criterio.
Tabla 10 Matriz de comparaciones de criterios con números reales
| C1 | C2 | C3 | C4 | Wi | |
| C1 | 1 | 1/2 | 3 | 1/4 | 0,1656 |
| C2 | 2 | 1 | 2 | 1/2 | 0,2402 |
| C3 | 1/3 | 1/2 | 1 | 1/5 | 0,091 |
| C4 | 4 | 2 | 5 | 1 | 0,5032 |
Fuente. Elaboración propia.
Estas nuevas ponderaciones se usaron como valores de entrada de TOPSIS.
Tabla 11 Proximidad relativa a la solución ideal con AHP
| d+ | d- | Ri | Ranquin | |
| A1 | 0,070 | 0,038 | 0,348 | 5 |
| A2 | 0,049 | 0,068 | 0,581 | 1 |
| A3 | 0,075 | 0,073 | 0,494 | 4 |
| A4 | 0,087 | 0,033 | 0,277 | 6 |
| A5 | 0,037 | 0,043 | 0,535 | 2 |
| A6 | 0,083 | 0,083 | 0,500 | 3 |
Fuente. Elaboración propia.
Aunque el nuevo ordenamiento es el mismo, se puede observar que con el método FAHP se logra una mejor discriminación entre las alternativas con respecto al ordenamiento con AHP, lo cual brinda al tomador de decisiones una mejor confianza en el proceso de selección.
6. Conclusiones
La apertura de un nuevo local comercial es un factor crítico para las empresas del sector minorista, ya que la decisión conlleva una serie de riesgos financieros. Así, uno de los factores más importantes a tener en cuenta es su ubicación (Roig-Tierno, Baviera-Puig, Buitrago-Vera y Mas-Verdu, 2013). Por esta razón, el objetivo principal de este estudio es la selección de la localización con una combinación entre AHP difuso y el método TOPSIS. En este sentido, se presentó un estudio de aplicación en Barranquilla, Colombia, a fin de decidir la ubicación de una nueva tienda de ropa deportiva.
Durante un proceso de selección se dispone de un conjunto de alternativas que, además de cumplir con los requisitos, presentan características homogéneas. Esto dificulta el proceso de decisión, ya que las diferentes preferencias que tienen cada uno de los expertos en relación con cada criterio probablemente harán que la decisión sea más difícil de tomar. Aunque existen otros métodos y diferentes enfoques, el modelo AHP difuso-TOPSIS reduce la incertidumbre y mejora la precisión de la selección.
En la primera parte del estudio de caso se establecen las alternativas y los factores que influyen en la ubicación de una tienda de ropa deportiva. Se utilizó la metodología del proceso de jerarquía analítica difuso. En la segunda parte se elabora un ranquin de los centros comerciales mediante la metodología TOPSIS. Dado que los criterios y su clasificación relativa pueden variar de un tipo de negocio a otro, los resultados no pueden generalizarse. Estos criterios van a variar de acuerdo con el tipo de negocio que se va a ubicar en el local a seleccionar, pero la integración del FAHP y TOPSIS es una buena herramienta para incorporar la importancia de los criterios a tener en cuenta. Se realizó una comparación al ponderar los criterios mediante el proceso de jerarquía analítica. Se destaca que con la metodología desarrollada en este estudio se logra una mejor discriminación de los resultados, lo que brinda una mayor confianza en el proceso de selección.
Aunque los resultados finales pueden diferir, la metodología propuesta también se puede aplicar en otros sectores de negocios tales como el de restaurantes, sectores de servicios, centros de belleza, joyerías y almacenes de calzado, entre otros. El análisis de sensibilidad mostrado en el presente estudio muestra la solidez de la herramienta.
De esta forma, al utilizar el método de toma de decisiones del científico presentado en este documento, cualquier persona que tome decisiones encontrará una forma efectiva y confiable de seleccionar la mejor opción en un grupo de alternativas, y podrá cuantificar el valor subjetivo que tiene para cada opción según los diferentes criterios.