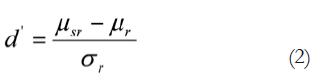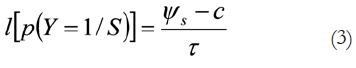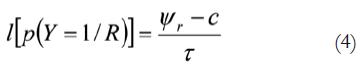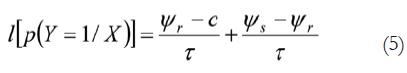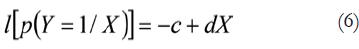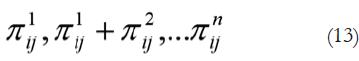ARTÍCULO

Modelos matemáticos en memoria de reconocimiento de palabras: un análisis roc multinivel

Mathematical Models in Word Recognition Memory: A Multilevel Analysis Roc

Manuel Pelegrina del Río
Agustín Wallace Ruiz
Universidad de Málaga

Enrique Emberley Moreno
Centro del Profesorado Campo de Gibraltar

Ricardo Tejeiro Salguero
Universidad de Cádiz

La correspondencia relacionada con este artículo debe ser enviada a Avda Cervantes 2 - 29071, pelegrina@uma.es

Recibido: Mayo de 2010 Aceptado: Septiembre de 2011

Resumen

En esta investigación se muestran los modelos más eficientes desde el punto de vista experimental y formal para la evaluación de la memoria de reconocimiento de ítemspalabras: En primer lugar se muestra un modelo matemático general que subyace a las diferentes formas de registro de datos. En segundo lugar se controla experimentalmente la elección, organización y tiempos de presentación del estímulo (ítems-palabras en castellano). En tercer lugar se aplica un análisis multinivel para modelar todos los niveles de respuesta de los participantes en las pruebas de memoria de reconocimiento. En cuarto lugar, se evalúa mediante escalas de estimación (EE) y mediante las características operativas del receptor (ROC) propias de la teoría de la detección de señales (TDS) y de los modelos de umbral. Los resultados concuerdan principalmente con un modelo de detección de señales, cuando los estímulos son palabras de frecuencia alta, y con un modelo de umbral (o de diferente varianza) cuando los estímulos son palabras de clase abierta; mientras que las palabras de frecuencia baja ocupan un lugar intermedio, situado entre la TDS y los modelos de umbral.

Palabras clave: Reconocimiento de ítems, análisis ROC, modelado estadístico y matemático.

Abstract

In this research we show the best efficient models in the evaluation of the recognition memory: First, a general mathematical model which underlies different data records ways. Second the election, organization and the presentation time of the stimulus is controlled experimentally. Third, we show the multilevel analysis for the rating scales, and a ROC and z-ROC distribution for the discrimination between TDS models and the threshold models. The results agree mainly with a TDS model when the stimuli are high frequency words, a model of threshold (or unequalvariance) when the stimuli are open class words, whereas the low frequency words occupy an intermediate place located between the TDS model and the threshold model.

Keywords: Items recognition, ROC analysis, statistical and mathematical modelling.

Introducción

La propuesta que se presenta consiste en un desarrollo de la idea inicial sobre modelado estadístico propuesta por McCullagh y Nelder (1989), desarrollada en otra investigación (Pelegrina, Beltran & Jiménez, 2007; ver también DeCarlo, 1998), a la que se incorpora el modelo multiestimador (multirater) propuesto por Johnson (1996), así como por Johnson y Albert (1999). A esta propuesta se incluye el análisis multinivel (ver Ishwaran & Gatsonis, 2000). Todo ello mediante la TDS (teoría de detección de señales) y las curvas ROC (acrónimo de Recevier Operating Characteristic, en español Característica Operativa del Receptor), ver por ejemplo Wixted (2007), y también Yonelinas y Park (2007) en los que ya se observa una idea integradora de diferentes modelos. Estos modelos tienen su inicio en la década de 1950 y 1960 (por ejemplo, Egan, 1958; Green & Swets, 1966; Wickelgreen & Norman, 1966).

Mediante la integración de lo anterior se pretende alcanzar los objetivos siguientes: (a) elaborar un modelado estadístico formal que incluya diseños experimentales en un sentido amplio; (b) utilizar ítems-palabras, aplicando en lo posible criterios estadísticos o formales: frecuencia y clase de palabras y sus correspondientes tiempos de presentación para su procesamiento en memoria; (c) considerar principios de análisis multinivel para los distintos valores obtenidos a partir de las escalas de estimación (EE); (d) registrar los datos mediante TDS y representarlos mediante curvas ROC y z-ROC. Todo ello con el objeto de elaborar modelos de memoria de reconocimiento de ítems. Desde la memoria de reconocimiento se pretende evaluar la continuidad o discontinuidad de las respuestas. Y dentro del "continuo", observar si hay variaciones y cómo pueden interpretarse, si mediante curvas ROC, mediante curvas z-ROC o incluso, mediante algún modelo híbrido (e.g. Yonelinas & Parks, 2007; Wixted, 2007). Se pretende además situar los resultados en diferentes niveles según dependan de uno u otro tipo de estímulo, aspecto enfatizado por Glanzer, Hilford y Kim (2007). En este sentido proponemos la evaluación y modelado de lasrespuestas SÍ-NO, y de todos los niveles de respuesta de la correspondiente escala de estimación.

En primer lugar, es importante conectar la parte empírica (datos) y la formal (estadística). Así, los datos más sencillos en un diseño experimental de memoria de reconocimiento de ítems consisten en presentar las respuestas SI-NO mediante el índice discriminación de MacMillan y Creelman (1991):

Donde ψ_s es la moda de la distribución de la señal y ψ_r es la moda de la distribución del ruido, mientras que τ es la una desviación estandarizada (DeCarlo, 1998; Hasselblad & Hedges, 1995).

El citado índice (fórmula 1), se puede considerar como una formulación no paramétrica de la d':

Donde el índice d' es la diferencia entre la media estimada de respuestas SÍ a la señal ( µ_sr ) y SÍ al ruido ( µ_r), dada en términos de la desviación típica del ruido σ_r.

Por sustitución y extrapolación, el índice de discriminación presentado en la fórmula 1 y 2 se puede escribir también como un modelo logit:

Donde d adquiere un valor de función probabilística logit, , Y representa las respuesta SI a la señal S cuando sólo hay dos posibilidades de respuesta, c representa el sesgo (o criterio de respuesta) y τ es la desviación.

Para el ruido, y desde el mismo modelo logit, la ecuación equivalente es:

Donde S se ha sustituido por el ruido R.

Se acepta que R y S son dos niveles de la variable respuesta e integramos las fórmulas 1, 3 y 4:

En la fórmula 5 se ha supuesto que el participante aplica, al menos, un sesgo c que representa un punto de corte (o criterio) en el continuo sensorial. En ese caso la fórmula 5 se puede transformar en:

En la que aparecen dos niveles de respuesta. Un nivel derivado de c, y otro de la variable X. Esto representa el predictor lineal más elemental en TDS con el sesgo (o criterio) de respuesta y la sensibilidad respectivamente. El modelo puede ser sustituido miembro a miembro por un modelo lineal (Agresti, 1989):

Donde π₁ indica la probabilidad de discriminación de una categoría que depende del intercepto α y de la variable X, a la que añadimos su correspondiente parámetro β. Si generalizamos para una escala de estimación, donde hay más de dos posibilidades de respuesta, obtenemos:

En la fórmula 8, j es un conjunto de valores ordenados (DeCarlo, 1998) que pueden representar un conjunto de respuestas del sujeto (una escala de estimación) con un determinado valor de la variable X. Esto se puede representar de una forma general mediante la siguiente fórmula:

Estas respuestas acumuladas por niveles de 1 a 5 nos permiten representan las curvas ROC . En efecto, si suponemos un intercepto que parte de un valor cero de la variable independiente, con cinco niveles de respuesta y con resultados consistentes (pendiente bien definida) podríamos también representar los datos mediante un modelo de regresión:

Este modelo es adecuado para predecir los resultados de la curva z-ROC propia de la TDS, en el sentido de una regresión lineal con una constante cuadrática próxima a cero, y una pendiente lineal de z-ROC próxima a la unidad tal como proponen Glanzer, Hilford y Kim (2004). Pero si consideramos las respuestas desde un modelo categórico logit multivariado, entonces:

Donde, s = 1, 2,...t-1, siendo t cuatro de las categorías de respuesta que dan lugar a proporciones acumuladas y donde el modelo nulo, que se puede tomar como referencia, es el valor 5 de la escala de estimación. Generalizando, un modelo logit acumulado para un modelo simple de dos niveles vendría dado por:

Donde, s = 1, 2,...t-1, siendo t las categorías de respuesta que dan lugar a proporciones acumuladas. Si se retoma lo anterior y se consideran dos o más niveles de probabilidad acumuladas de las respuestas, entonces tendremos:

Optar por la descripción de los datos según el modelo de la fórmula 10, modelo continuo, o 13 depende de la naturaleza de éstos y de la consistencia de las medidas. También depende del investigador; en el primer caso utiliza la estadística clásica y la TDS clásica, en el segundo, los modelos lineales generalizados y el modelado estadístico.

En este sentido Johnson (1996) y Johnson y Albert (1999) han propuesto un modelo general que incluye el modelado de datos procedente de escalas ordinales:

Donde x es una variable latente y θ es el punto de corte de los estimadores (jueces, evaluadores, participantes...). Un estado superior de la ecuación anterior en el ámbito ROC multinivel, mediante escalas de estimación, se puede escribir mediante la fórmula:

En la fórmula 15 g es la distribución posterior conjunta, representa el conjunto de rasgos latentes percibido por los participantes para una puntuación determinada. Es una abstracción matemática de la escala de estimación en la que se han obtenido las puntuaciones "i" representadas en los puntos de las curvas ROC a partir de sus correspondientes escalas de estimación y para cada una de las condiciones experimentales (tipo de estímulos en memoria), Z es la matriz de densidad de probabilidades que incorpora todas las posibles respuestas, γ es el punto de corte (criterio) de los participantes, que en la curva ROC se representa por la diagonal negativa o línea del azar, s² _j es la varianza que puede observarse cuando se comparan las curvas ROC mediante su simetría respecto a la diagonal negativa (es determinante para diferenciar entre modelos propios de la TDS y modelos de umbral), a y b son dos posibles variables a comparar, en la aplicación aciertos y falsas alarmas respectivamente; α denota la relación de probabilidad en una función de distribución de probabilidades resultado de los tratamientos j en un tiempo determinado T, x es la curva ROC con sus respuestas i en las condiciones j, Z es el sesgo de respuesta, y E indica la escala de estimación dentro del intervalo 1 a 5 (en la aplicación es una escala ordinal, curva ROC que se ha convertido en escala de intervalo z-ROC).

La ecuación 15 representa un modelo global mientras que las ecuaciones que le preceden se propone, son modelos dicotómicos y politómicos, con posibilidades de registrar las respuestas según modelos discretos o continuos. Así, se describe la posibilidad de obtener respuestas continuas según la TDS, lo que permitiría obtener distribuciones ROC propias de este modelo, pero también la posibilidad de que ante un cambio de sensibilidad del participante frente a un tipo u otro de variable, se puedan obtener resultados con diferente varianza, o umbrales de respuesta. Se ha de indicar que donde algunos autores evalúan en términos de varianza (Wixted, 2007), otros prefieren el de umbrales (Rouder & Morey, 2009), sin excluir el conocido doble proceso: familiaridad y "recollection" de Yonelinas (1999), así como otras posiciones integradoras, o híbridas que comentamos en este trabajo y que suponen una apertura hacia la aplicación de cualquier modelo ROC (e.g. Egan, 1975) en función de las variables y de los resultados obtenidos empíricamente.

El segundo modelo que se propone, se refriere al tratamiento del estímulo. Por un lado a la clasificación estadística del estímulo y por otro, a la regularidad o procedimiento experimental a seguir para controlar el tiempo de su procesamiento. Así, en la investigación se controló la media en frecuencia de uso de las palabras que se extiende desde 28 a 34130.5. También se controló la clase, la longitud y el número de palabras que se utilizaron. Esto es importante porque cuando se seleccionaron muestras de palabras en las que se incorporó frecuencia y clase las categorías, se enmascaran unas con otras, ya que las diferentes clases de palabras están afectadas sistemáticamente por diferente frecuencia (ver por ejemplo la estadística elaborada por Münte, et al. (2001) sobre frecuencia de uso de palabras en lengua alemana, donde plantea el mismo problema. Ver también otros ejemplos similares en Bröder y Schüz (2009) y Gorman (1961). En este sentido, como cita histórica obligada, se señala a Egan (1958) primer autor que, en un trabajo técnico muy relevante, incorpora la palabra como señal en el ámbito de la psicofísica y la TDS (Green & Swets, 1966). Esta incorporación ampliamente desarrollada por Egan (1975) produjo cierta controversia dada la discutible utilización de la palabra como estímulo propio de la TDS y de la psicofísica, debido a que la palabra es una señal compleja con la que se forman listas de ítems no estrictamente equivalentes ente sí (ver apartado "material" donde se presentan detalles específicos sobre el control del estímulo-señal en este contexto).

Por su parte, el tiempo de presentación del estímulo tiene efectos en la predicción de umbrales (o varianzas) versus distribuciones continuas de respuesta (Pelegrina & Tejeiro, 2006), trabajo en el que se comparan tiempos de exposición de 250 y 450 ms (ver en este sentido formas de control del tiempo y sus efectos a partir de 300 ms, en Boldini, 2004, y en general la importancia de su control para obtener respuestas diferenciadas, por ejemplo, Ruiz, Gallego-Largo, Conchillo, Recarte & Hernández, 2006). Efectivamente, a mayor tiempo en el procesamiento manteniendo constante el estímulo, más probabilidad de obtener al menos un umbral en memoria, o varianzas diferenciadas, y por tanto posibles curvas ROC basadas en el umbral. En este sentido, y de acuerdo con los autores que se acaban de citar, se acepta que a partir de 300 ms de exposición del ítem, hay un punto de inflexión en el continuo de respuestas.

Mediante la incorporación de un tercer modelo se incluyó un análisis multinivel con los mismos datos que utilizamos para elaborar las curvas ROC (ver Ishwaran & Gatsonis, 2000). El objetivo de este análisis consiste en estudiar los diferentes niveles de aciertos y falsas alarmas, explorando si hay o no diferencias significativas, no sólo entre las diferentes condiciones experimentales, sino además, entre los diferentes niveles de respuesta dentro de cada condición.

En cuarto lugar, se ha referido a los modelos de análisis de datos en memoria de reconocimiento. Aquí se incorporó una réplica de las regularidades propuestas por Glanzer, Hilford y Kim (2004). Los criterios propuestos por estos autores sirven para reflexionar sobre el tipo de curvas obtenido, especialmente se ha referido a si las curvas ROC son o no convexas y a si la pendiente de la curva z-ROC es igual o diferente de la unidad. Así, en el caso de presencia de umbral alto (Blackwell,1963) se obtendría un nivel a partir del cual es rememorada la palabra, mientras que cuando hay doble umbral (Bröder & Schütz, 2009) habría dos puntos de inflexión en el correspondiente continuo de respuestas.

A partir de lo anterior, se contrastó una hipótesis general mediante la cual suponemos que hay un continuo en la obtención del umbral en memoria de reconocimiento de ítems mediante palabras familiares, en nuestro trabajo, palabras muy frecuentes, que producirán curvas ROC continuas, de acuerdo con la TDS. Mientras que las palabras menos frecuentes, mediante un tiempo suficiente de procesamiento consciente (500 ms y en general niveles ligeramente superiores a 300 ms) producirán umbral, o bien diferentes varianzas si apelamos a la TDS. Un caso especial de umbral correspondería a las palabras de clase abierta, que dada su mayor discriminabilidad, proporcionaría aportaciones más altas y precisas de palabras. Todo ello manteniendo de forma rigurosamente constantes las condiciones experimentales.

Esta hipótesis incluye la clase de palabras (variable cualitativa) además de la frecuencia (variable cualitativa). La clase de palabra es dicotómica (clase abierta y cerrada) y el efecto de clase abierta suponemos hipotéticamente que en participantes adultos con nivel cultural medio, es más potente en memoria que el efecto de frecuencia. A partir de lo anterior, se elaboró un diseño con tres niveles en la clasificación de las palabras (clase abierta, frecuencia baja y frecuencia alta), dos niveles correspondientes a los aciertos y falsas alarmas, y cinco niveles correspondientes a la formas de respuesta mediante una escala de estimación.

Método

Participantes

La muestra estuvo conformada por 98 estudiantes (41 hombres 57 mujeres) entre 18 y 26 años (M=21.06, y DT=1.38). Todos ellos sin patología manifiesta y con una visión normal o corregida.

Materiales

En primer lugar se obtuvo una muestra de 120 palabras basada en la frecuencia de uso (alta y baja) y la clase (clase abierta). La frecuencia de uso en clase cerrada (CC) se situó entre 21 y 4708 en Juiland y Chang-Rodriguez (1964) y entre 35 y 67636 en el diccionario de Alameda y Cuetos (1995). Se calculó la media entre ambas series de palabras y se estimó la frecuencia entre 28 y 34130.5. La frecuencia de las palabras de CA (nombres, verbos y adjetivos) se situó entre 29 y 696 en Juiland y Chang-Rodriguez (1964) y entre 19 y 1798 en Alameda y Cuetos (1995). La media de la CA se situó entre 24 y 1247. Se observó que al clasificar palabras de CA se produce un desequilibro en la variable frecuencia, por lo que es necesario balancear clase y frecuencia de palabras para que sea válida la comparación entre condiciones experimentales. Esto ocurre también en otros idiomas (ver Münte et al., 2001).

A partir de estas palabras se organizaron tres condiciones experimentales: 40 palabras de FB, de las cuales 20 eran de CA y 20 de CC; 40 de FA, de las cuales 20 eran de CA y 20 de CC y 40 palabras de CA de las cuales 20 eran de FA y 20 de FB. La FA estaba formada por palabras de CA que oscilaban entre 104 y 1274 de frecuencia y palabras de CC que oscilaban entre 577 y 34130.5. La FB estaba formada por palabras de CA que oscilaban entre 24 y 80 de frecuencia y por palabras de CC cuya frecuencia oscilaba entre 28 y 539.5.

Procedimiento

Las tres listas de palabras fueron presentadas mediante el programa E-prime (Schneider, Eschman & Zuccolotto, 2002). El orden de presentación de las palabras para cada sujeto fue aleatorio, y el orden de presentación de las listas fue contrabalanceado, de forma que cada lista se presentó el mismo número de veces en la misma posición serial. El resto de parámetros: monitor, distancia del monitor, ángulo de visión y experimentador se igualaron por constancia para todos los participantes.

Se aplicó el paradigma de la TDS en memoria dereconocimiento de ítems, respuestas "SÍ-NO" más escala de estimación de entre 1 y 5 puntos. La respuesta "SÍ-NO" pretende obtener el registro en el mínimo tiempo de reacción posible, mientras que la escala de estimación pretende una valoración subjetiva por parte del participante de la fuerza del ítem en memoria. El 1 indica el nivel más bajo de estimación y el 5 el nivel más alto. La mitad de las palabras, 20 para cada condición, fueron consideradas señal y otras 20 ruido. Cada palabra permanecía 500 ms en pantalla y estaba precedida por un punto negro que permanecía en el centro de la pantalla durante 300 ms. Cada participante leyó las instrucciones hasta su compresión y realizó una prueba de entrenamiento previa al experimento. En el reconocimiento de ítems la palabra diana permanecía en pantalla hasta que el participante pulsaba, lo más rápido posible, la tecla correspondiente a SI o NO, 1 y 2 del teclado respectivamente. Sobre la precisión y rapidez de respuestas en memoria ver McNicol y Steward (1980). Inmediatamente después, el participante valoraba verbalmente su confianza en la respuesta dada mediante la escala de estimación subjetiva de cinco puntos (Torgerson, 1958). En todas las condiciones diferenciales del experimento se aplicó balanceo o contrabalanceo completo, según hubiera dos o más condiciones experimentales respectivamente.

Resultados

A los datos obtenidos se les aplicó un análisis de varianza (ANOVA). Las frecuencias altas y bajas de las palabras fueron estadísticamente significativas en el nivel 3 de la escala de estimación: F(1, 91)= 5.25, MCe= 1.03, p=.02, y para el nivel 4: F(1.91)= 10.02, MCe= 0.74, p=.002.

Para la clase abierta se obtuvo significación estadística en los cinco niveles de la escala de estimación (EE) que presentamos a continuación ordenados del uno al cinco: F(1, 91)= 11.29, MCe= 1.29, p=.001; F(1, 91)= 30.81, MCe= 1.07, p=.0001; F(1, 91)= 6.22, MCe= 1.13, p=.014; F(1, 91)= 44.95, MCe= 0.75, p=.0001; F(1, 91)= 3.96, MCe= 0.69, p=.05. Para comparar de forma más exhaustiva los niveles de las EE aplicamos un análisis multinivel, a partir de las respuestas obtenidas en la escala de estimación, y de acuerdo con las fórmulas 10 a 15, estableciendo los niveles empíricos correspondientes, ver ejemplo similar en Wilson y Nielsen, (2008). En este modelo no se representa el punto 5 por ser el modelo nulo. Los valores entre paréntesis representan el error típico de estimación.

La ratio entre estimador y su error típico sigue una distribución t. Cuando el cociente es mayor que 2, el estimador se acepta como significativo. Todos los valores beta correspondientes al modelo multinomial son significativos menos el valor 'EE1' del modelo A. En el valor aciertos- falsas-alarmas (ACI-FAA) son significativos los modelos B, C, D y E. En los valores CA son significativos los modelos C y E. En los valores FA-FB es significativo el modelo E, ver tabla 1.

El análisis de los parámetros y curvas ROC (tabla 2) presenta una d' que crece progresivamente en el siguiente orden: FA < FB < CA; d'= 0.39 < 0.62 < 0.84. Su correspondiente medida no paramétrica es consistente con este resultado: área bajo la curva ROC = 0.54 < 0.67< 0.72. El valor negativo de las constantes cuadráticas de las curvas ROC muestran que éstas son convexas: CC = -0.30 < -0.32 < -1.80 creciendo respectivamente hacia una tendencia negativa en el mismo sentido de los datos anteriores. Por el contrario, en las curvas z-ROC las CC son positivas. Además, los resultados de la pendiente de los mismos valores de la curva z.ROC ofrece dos tipos de valores: Uno próximo a la unidad, pendiente de la FA= 0. 99; lo que nos permite aceptar un modelo próximo a la TDS y dos modelos de umbral: FB = 0.82 y CA = 0.76. En la figura 1 (A, B y C, D, E y F) se observan las distribuciones respectivas con evidencia de resultados según la TDS y los modelos de umbral. Esto se constata en el ajuste progresivo desde una función en forma de U en la CA, a una línea recta en la FA en las curvas z-ROC pasando por una situación intermedia en las palabras de FB.

Discusión

Los resultados del ANOVA confirman la hipótesis de que la frecuencia baja se discrimina mejor que la frecuencia alta, en el sentido que ya se conoce en el denominado "efecto espejo" y de que el efecto de clase abierta es superior al efecto de frecuencia en estudiantes adultos. A partir de aquí se infiere que el acceso al léxico sigue un doble proceso, uno para la clase y otro para la frecuencia. Por consiguiente, se asume que el umbral (o varianza) correspondiente a la clase de palabras denominada abierta es de naturaleza distinta al umbral (o varianza) correspondiente a la frecuencia baja de palabras.

Así, en la figura 1F, se observa una representación del proceso de "familiaridad", mediante la evidencia de una z-ROC recta (ver Glanzer, Hilford & Kim, 2009).

La familiaridad es un proceso relativamente rápido que se refiere a la fuerza de un ítem en memoria. Tradicionalmente se ha modelado estadísticamente con palabras de alta frecuencia de uso mediante una distribución propia de la TDS, ver además Atkinson y Juola (1974), Jacoby y Dallas (1981), y Mandler (1980), entre otros. En general, los estímulos muy familiares, por ejemplo, el reconocimiento de rostros (e.g. Pitarque, Algarabel & Aznar, 2007), palabras muy frecuentes, o acciones muy cotidianas y comunes, se vienen ajustando al modelo clásico de la TDS. Pero en palabras de CA y FB hemos obtenido distribuciones que se identifican con procesos de recollection, según el modelo propuesto por Yonelinas, (1999).

Hemos de indicar aquí que hay muchos autores, muy distantes en el tiempo, que han mantenido a lo largo de varios años, un modelo experimental integrador en lo que se refiere a continuos de respuesta versus umbral (e.g. Coombs, Dawes & Tversky, 1970; Egan, 1958). Recientemente, Wixted (2007) ha propuesto un modelo de detección de señales de desigual varianza, "unequal-variance signal detection (UVSD) model" y afirma que los procesos de decisión en memoria no representan un proceso puro, sugiriendo la necesidad de investigar en diferentes vías los "múltiples" correlatos de la memoria de reconocimiento.

Nuestros resultados pueden ser incorporados en un modelo general empírico que incluye regularidades ya establecidas en el reconocimiento de fuentes de memoria y el reconocimiento de ítems en el contexto de la TDS (ver Glanzer, Hilford & Kim, 2004). Insistiendo en ello, estos mismos autores muestran que las ROC son convexas (ver además Egan, 1958), que las z-ROC son lineales, las pendientes de las z-ROC son menores que 1.00, y que los cambios de pendiente de las z-ROC decrecen con el incremento de la precisión de acuerdo con el siguiente patrón: SN<WN<WO<SO, donde O indica ítems señal (o viejos), N = ítems nuevos, S= fuerte, W =débil. Este orden define el efecto espejo, resultado de los aciertos y falsas alarmas en la distribución de respuestas SÍ- NO o del promedio de los datos en la escala de estimación (Glanzer, Hilford & Kim, 2004).

Se ha de indicar también que al haber incluido la frecuencia y clase en el procesamiento de palabras se ha planteado un contraste de hipótesis crucial: continuidad frente a umbral. Por ello, lo que se ha propuesto, como hipótesis de trabajo, consiste en una integración de técnicas que dejen abierta la posibilidad de evaluar teorías duales y multiproceso en memoria de reconocimiento, de una forma integrada desde el punto de vista del registro de datos y del análisis, en lo que supone un desarrollo (entre todos los propuestos) del modelo propuesto por Goldstein (1995) en el ámbito del análisis ROC. Ese tratamiento mutinivel contribuye también a una propuesta general y unificada sobre el modelado de los procesos de memoria.

En este sentido, el modelado de los resultados mediante un modelo multinivel (tabla 1), ha proporcionado ajustes diferenciados. En efecto, las variables de escalamiento correspondientes a ACI-FAA, CA y FA-FB aparecen como estructuras diferentes porque en ACI-FAA se obtienen cuatro modelos significativos: B, C, D y E. En el valor AC se obtienen dos modelos significativos: el C y el E y el valor FA/FB da lugar también a un modelo significativo. Además, cuando comparamos escalamiento (EE con cuatro puntos y variables independientes) y modelos A, B, C, D y E, observamos diferencias cuantitativas y cualitativas.

Sobre nuestros resultados y en relación a las teorías explicativas se puede asumir que los estímulos muy familiares se ajustan a un modelo continuo de respuestas predicho por la TDS y tratado por Bröder y Schütz (2009). Aunque estos autores prefieren el término evidence strength (p. 587), al término "familiaridad", porque "fuerza" es un término con menos implicaciones teóricas. Strenght es el término utilizado tradicionalmente en memoria de palabras mediante el paradigma de la TDS (Wickelgren & Norman, 1966).

Estos autores prefieren dejar el término familiaridad diferenciado de recollection para el modelo propuesto por Yonelinas (1999), en el que la familiaridad representaría la TDS y recollection un modelo de umbral alto.

En conclusión, desde el trabajo de Egan (1958) se ha venido investigando si los datos de la memoria de reconocimiento se adaptan mejor a un modelo de detección de señales o a un modelo de umbral. Se ha obtenido dos modelos bien diferenciados, un modelo se acomoda mejor a la TDS, figura 1F, con pendiente lineal próxima a la unidad. Los otros dos resultados se parecen más a modelos de umbral, figura 1D y 1 E.

Por otra parte, para explicar estos resultados, y en fechas recientes, se han propuesto modelos mixtos, que integran la TDS y el umbral, entendidos estos como modelos de la TDS con desiguales varianzas (Wixted, 2007). De esta manera, los resultados de las curvas ROC pueden ser igualmente explicados por la TDS y los modelos de umbral. Bröder y Schütz (2009) y Yonelinas y Parks (2007) proponen que los modelos deben dar cuenta de los "datos existentes en las curvas ROC" empíricas. Nuestros datos aportan evidencia de que, efectivamente, en el reconocimiento de ítem hay que incorporar modelos que van más allá de la familiaridad (Algarabel & Pitarque, 2007; Boldini, Russo & Avons, 2004).

Finalmente, asumiendo las propuestas vigentes que se acaban de citar, extrapoladas a estímulos en lengua castellana, se ha propuesto además modelado estadístico en el que se observan respuestas dicotómicas y politómicas, y se ha avanzado en la reconsideración del estímulo para ser evaluado, ya que desde el control del estímulo se realizan los primeros pasos para predecir un modelo u otro. En definitiva, hoy se puede asumir, que el investigador está más cerca de poder predecir a cuál de los modelos se adaptarían mejor sus resultados, así como a la posible modelización de los mismos, con el fin de extraer matices, características y distribuciones cada vez más precisas con respecto a la evaluación de las respuestas dadas por los participantes en tareas de memoria y ante diferentes variables.

Referencias

Agresti, A. (1989). Tutorial on modeling ordered categorical response data. Statistics bulleting, 105, 290-301.        [ Links ]

Alameda, J.R. & Cuetos, F. (1995). Diccionario de frecuencias de las unidades lingüísticas del castellano. Universidad de Oviedo. Departamento de Psicología        [ Links ]

Algarabel, S., & Pitarque, A. (2007). ROC parameters in item and context recognition. Psicothema, 19 (1), 163-170.        [ Links ]

Arndt, J., & Reder, L.M. (2002). Word frecuency and receiver operating characteristic curves in recognition memory. Journal of Experimental Pychology: Learning, Memory, and Cognition, 28 (5), 830-842.        [ Links ]

Atkinson, R.C., & Juola, J.F. (1974). Search and decision processes in recognition memory. In D.H. Krantz, R.C. Atkinson, R.D. Luce, & P. Suppes (Eds.), Contemporary developments in mathematical psychology: Vol. I. Learning, memory & thinking (pp. 242-293). San Francisco: Freeman.        [ Links ]

Blackwell, H.R. (1963). Neural theories of simple visual discrimination. Journal of the Optical Society of American, 53, 129-160.        [ Links ]

Boldini, A., Russo, R., & Avons, S.E.(2004). One process is not enough! A speed-accuracy trade-off study of recognition memory. Psychonomic Bulletin & Review, 11, 353-361.        [ Links ]

Bröder, A., & Schütz, J. (2009). Recognition ROCs are curvilinerar-or are they? On premature arguments againts the two- high-treshold model recognition. Journal of Experimental Psychology: Learning Memory and cognitio, 35, 3. 587-06.        [ Links ]

Coombs, C.H., Dawes, R.M., & Tversky, A. (1970). Mathematical Psychology. New Jersey: Prentice-Hall.        [ Links ]

DeCarlo, L.T. (1998). Signal detection theory and generalized linear models. Psychological methods, 3 (2), 186-2005.        [ Links ]

Egan, J.P. (1958). Recognition memory and operating characteristic. Technical Note AFCRE-IN-58-51.        [ Links ]

Egan, J.P. (1975). Signal detection theory and ROC analysis. New York: Academic Press.        [ Links ]

Glanzer, M., Hilford, A., & Kim, K. (2004). Six regularities of source recognition. Jounnal of Experimental Psychology: Learning, Memory and Cognition, 30 (6), 1176-1195.        [ Links ]

Goldstein, H. (1995). Multilevel Statistical model (2ª Ed.). London: Edward Arnold.        [ Links ]

Gorman, A.M. (1961). Reecognition memory for nouns as a function of abstractness and frequency. Learning, Memory, and Cognition, 25, 500-513.        [ Links ]

Green, D.M., & Swets, J.A. (1966). Signal detction and psychophysics. New York: John Wiley.        [ Links ]

Hasselblad, V., & Hedges, I.V. (1995). Meta-analysis of screening and diagnostic tests. Psychological Bulletin, 117, 167-178.        [ Links ]

Ishwaran, H., & Gatsonis, C.A. (2000). A general class of hierarchical ordinal regression models with applications to correlated ROC analysis. The Canadian Journal of Statistic, 28 (7), 1-23.        [ Links ]

Jacoby, L.L., & Dallas, M. (1981). On the relationship between autobiographical memory and perceptual learning. Journal of Experimental Psychology: General, 2 (110), 139-154.        [ Links ]

Johnson, V.E. (1999). On bayesian analysis of multirater ordinal data: An application to automated essay grading. Journal ot the American Statistical Association, 91 (433), 42-51.        [ Links ]

Johnson, V.E., & Albert, J.H. (1999). Ordinal data modeling. Springr-Verlag: New York.        [ Links ]

Juiland, A. & Chang-Rodríguez, E. (1964). Frequency diccionary of Spanish words. Mouton and Co.: La Haya.        [ Links ]

MacMillan, N.A. & Creelman, C.D. (1990). Response bias: Characteristics of detection theory, threshold theory , and "non parametric" indexes. Psychological Bulleting, 107, 401-413.        [ Links ]

Mandler, G. (1980). Recognizing: The judgment of previous occurrence: Psychological Review, 87, 252-271.        [ Links ]

McCullagh, P., & Nelder, J.A. (1989). Generalized linear models. London: Chapman and Hall.        [ Links ]

McNicol, D., & Steward, G. W. (1980). Reaction time and the study o memory. In A. T. Welford (Ed.). Reaction times. (pp. 253-307). New York: Academic Press.        [ Links ]

Pelegrina, M., Beltran, F.S., & Jiménez, A. (2007). Sentences recognition memory and extraversión-introversion levels: A statistical modelling aproach. Quality & Quantity, 41, 627-633.        [ Links ]

Pelegrina, M., & Tejeiro, R.. (2006). Parámetros ROC y z-ROC en memoria de palabras: Efectos experimentales y preeperimentales, 18 (1), 160-164.        [ Links ]

Pitarque, A., Algarabel, S. & Aznar-Casanova, J.A. (2007). Familiaridad y recuerdo en el reconocimiento de rostros ficticios: Implicaciones de los modelos de reconocimiento. Psicothema, 19, 565-571.        [ Links ]

Pulvemüller, F., Lutzenberger, W., & Birbaumer, N. (1995). Electrocortical distinction of vocabulary types. Electroencephalography and Clinical Neurophysiology, 94, 357-370.        [ Links ]

Ruiz Gallego-Largo, T., Conchillo, A., Recarte, M., Hernández, M.J. (2006). Dependencia serial en la estimación de llegada de un coche. Psicothema, 18 (4), 738-742.        [ Links ]

Schneider, W., Eschman, A., & Zuccolotto, A. (2002). E-Prime reference guide. Pittburgs: Psychology Software Tools Inc.        [ Links ]

Torgerson, W. S. (1958). Theory and methods of scaling, New York.        [ Links ]

Yonelinas, A.P. (1999). The contribution of recollection and familiarity to recognition and source-memory judgments: A formal dual-process model and an analysis of receiver operating characteristics. Journal of Experimental Pychology: Learning, Memory, and Cognition, 25, (6), 1415-1434.        [ Links ]

Yonelinas, A.P. & Parks, C.M. (2000). Receiver operating characteristics in recognition memory: A review. Psychological Bulletin, 133 (5), 800-832.        [ Links ]

Wickelgren, W.A., & Norman, D.A. (1966). Strength models and serial position in short-term memory. Journal of Mathematical Psychology, 3, 316-347.        [ Links ]

Wilson, C., & Nielsen, K. (mayo, 2008). Hierarquical bayesian modelling of multi-level phonetic imitation. 16 th annual CUNY Conference on human Sentence Processing, Cambridge.        [ Links ]

Wixted, J.T. (2007). Dual-process theory and signal - detection theory of recognition memory. Psychological Reiew, 114 (1), 152-176.        [ Links ]