INTRODUCCIÓN
Las plantaciones de Hevea brasiliensis (caucho) son apetecidas alrededor del mundo por su valor económico y su importancia social (Fox et al., 2012). Theobroma grandiflorum (copoazú) es un frutal amazónico ampliamente conocido en la región que ocasionalmente se produce en asociación con H. brasiliensis (Orjuela-Chaves et al., 2014; Sterling et al., 2015). En 2019 se cultivaron más de 12.3 millones de hectáreas de H. brasiliensis para la producción de látex en zonas tropicales, principalmente en el sur y sureste asiático y en África occidental, mientras que el país con mayor área en América del Sur fue Brasil, con 159 mil hectáreas (FAO, 2021). En 2020, Colombia presentaba alrededor de 8400 ha de caucho natural (FAO, 2021).
Una de las estrategias más empleadas para combatir el cambio climático es la captura de carbono (Chapman et al., 2020; Doelman et al., 2020; Rosenstock et al., 2019; Silva et al., 2019), la cual puede lograrse con sistemas forestales y/o agroforestales (Gomes et al., 2020; Kongsager et al., 2013; Ramachandra & Bharath, 2019). La compensación de emisiones por medio de plantaciones, entre estas las de H. brasiliensis, puede utilizarse en proyectos REDD+ (reducción de emisiones por deforestación, degradación forestal e incremento en almacenamiento de carbono) (Fox et al., 2012; Kongsager et al., 2013), lo cual también incluye la interface entre bosques, plantaciones y agricultura (Minang et al., 2014).
Se sabe que las plantaciones de caucho tienen un alto potencial para almacenar carbono, tal como estimaron Kongsager et al. (2013) en Ghana, quienes afirman que estas plantaciones tienen el mayor potencial de almacenamiento (214 Mg.ha-1, superior a lo encontrado en cacaotales y plantaciones de naranja y palma de aceite). A pesar de estos hallazgos, las estimaciones de biomasa en estos sistemas de producción presentan una gran variación (Tang et al., 2009). Por tal motivo, es importante desarrollar modelos locales para reducir la incertidumbre en las estimaciones (Andrade et al., 2018; IPCC, 2013), con el fin de implementar estudios de ciclaje de nutrientes y carbono (Dossa et al., 2008). El desarrollo de modelos locales permite alcanzar un Nivel 2 (Tier 2) en las estimaciones de biomasa y carbono (IPCC, 2013).
Los modelos alométricos permiten la predicción de la biomasa mediante características dasométricas de fácil medición como el diámetro del tronco. Dichas características son factores clave para la estimación de la contribución de los ecosistemas forestales al ciclo de carbono (Andrade et al., 2018; Picard et al., 2012). El desarrollo de modelos de biomasa basados en la cobertura arbórea o área de la copa es fundamental para impulsar los métodos de investigación en este campo y las metodologías de monitoreo de la captura de carbono (Anaya et al., 2009; IPCC, 2003; Meyer et al., 2018). Por ejemplo, en Colombia se han desarrollado modelos de biomasa aérea para pasturas y bosques naturales usando sensores remotos y cobertura arbórea (Anaya et al., 2009). En este sentido, el objetivo de este trabajo fue desarrollar modelos alométricos para la predicción de la biomasa aérea y subterránea en árboles individuales de H. brasiliensis y T. grandiflorum en la Amazonía colombiana.
MATERIALES Y MÉTODOS
Área de estudio. El estudio se realizó en el departamento del Caquetá, situado en el noroeste de la región de la Amazonía colombiana, entre las coordenadas 00º42´17’’S y 02º04’13’’ N y 74º18’39’’ y 79º19’35’’ O. Este departamento cuenta con una superficie de 88 965 km2, lo cual representa el 7.8 % del territorio nacional. La investigación se desarrolló en los municipios de El Doncello, Florencia y Belén de los Andaquíes, cuyo rango de altitud es de 312-480 m, con 26 ºC de temperatura promedio, y 3500-3540 mm.año-1 de precipitación promedio (Figura 1).

Figura 1 Localización del área de estudio: El Doncello, Florencia y Belén de los Andaquíes, Caquetá, Colombia.
Selección de los sistemas de producción. Con el apoyo de la Asociación de Reforestadores y Heveicultores del Caquetá (ASOHECA), se seleccionaron nueve fincas, tres por municipio, de producción tradicional de caucho (Hevea brasiliensis (Willd. ex A.Juss.) Müll. Arg.) que estuvieran ubicadas en los sitios previstos de mayor concentración de cultivos de caucho en cada municipio. Se seleccionaron plantaciones de H. brasilienses en monocultivo y sistemas agroforestales (SAF) con copoazú (Theobroma grandiflorum (Willd. ex Spreng.) K. Schum.). Las plantaciones de monocultivo contaban con un espaciamiento de 7 x 2.8 m, mientras que en los SAF se empleaban líneas dobles de caucho a 3 x 3 m, con un espaciamiento de 7 m entre hileras dobles.
Selección de individuos. Se seleccionaron 41 árboles de H. brasiliensis, sin importar su clon, de entre 1 y 50 años de edad, con un rango de diámetro a la altura del pecho (DAP) de 3.2 a 49.7 cm y una altura total (AT) entre 3.4 y 21.6 m. Los árboles muestreados correspondieron a los clones IAN 710, FX 3864, FDR 5788, FX 4098 y FX 25. Asimismo, se seleccionaron 40 árboles de T. grandiflorum con diámetro del tronco a 30 cm de altura (D30) entre 3.3 y 23.6 cm y una AT de 2.1 a 7.6 m. Los árboles seleccionados eran típicos de su especie y tenían dimensiones de acuerdo con el rango de tamaños comúnmente encontrados en estos sistemas de producción. Se consideraron clases diamétricas para tener varios individuos de cada clase. Todos los individuos seleccionados provenían de fincas con topografía ondulada y características muy similares en los tres municipios de estudio. En el mismo sentido, se procuró que la distancia entre los individuos muestreados fuera igual o mayor a 250 m. De estos individuos, 19 de H. brasiliensis (1.9 < DAP < 50.2 cm) y 12 de T. grandiflorum (2.4 < D30 < 24.4 cm) fueron aleatoriamente seleccionados de diferentes clases diamétricas, en aras de extraer su sistema radicular para la construcción de modelos de biomasa subterránea.
Medición, corte y estimación de biomasa. Se midieron los siguientes parámetros en los individuos seleccionados: el diámetro del tronco (DAP para H. brasiliensis y D30 para T. grandiflorum), la altura total (AT), la altura a la base de la copa (AB) y el área de la copa (AC), estimada como un círculo midiendo dos diámetros perpendiculares de la proyección de la copa. Los diámetros de los troncos se midieron con cinta diamétrica y las alturas y los diámetros de copa con cinta métrica. Estas dimensiones fueron tomadas estando los árboles en pie, pero luego se verificaron las alturas una vez se cosecharon los árboles. Los individuos seleccionados se cortaron lo más bajo posible y se procesaron el mismo día para reducir el error por pérdida de humedad de la materia fresca e inicio del proceso de descomposición. Cada árbol fue dividido en componentes (fuste, ramas y hojas), los cuales se pesaron en fresco, tomando una submuestra de cerca de 300 g para para estimar la materia seca (60 °C hasta llegar a peso constante) y calcular la biomasa por componente y total por individuo.
La extracción de los sistemas radiculares para la estimación de la biomasa subterránea se realizó empleando el método de excavación semimecánica, que consiste en la excavación manual de la raíz apoyada por tracción mecánica. Los sistemas radiculares se extrajeron de un polígono de Voronoi delimitado por la mitad de las distancias entre un individuo y su vecino más cercano (Defrenet et al., 2016; Levillain et al., 2011), asumiendo que las raíces que quedan por fuera del polígono son compensadas por aquellas de las plantas vecinas dentro del mismo. Posteriormente, las raíces se limpiaron manualmente y se separaron por clases de tamaño, tomando las gruesas (diámetro>2 mm). Luego se pesaron en húmedo y se llevaron muestras de 300 g al laboratorio para determinar el contenido de humedad. De la misma forma, se estimó la relación entre la biomasa subterránea y aérea (B b /B a ).
Prueba y selección de los modelos de mejor ajuste. Se probaron los supuestos de normalidad, independencia y homegeneidad de varianzas. El supuesto de normalidad se evaluó mediante la prueba de Shapiro Wilk modificada y la gráfica Q-Q. Se verificó el supuesto de independencia para garantizar que las unidades de muestreo no dependieran de la homogeneidad de varianza, utilizando el grafico de dispersión de residuos vs. predichos.
Se realizó el análisis de correlación de Pearson entre las variables dependientes (biomasa aérea y subterránea) y las independientes (D30, DAP, AT, AB y AC) para observar cuáles variables dasométricas explicaban mejor la biomasa. Se probaron modelos genéricos, algunos con transformaciones logarítmicas (Loetsch et al., 1973), con la biomasa como variable dependiente en función de aquellas variables independientes con las q tuvo mejor coeficiente de correlación (Andrade et al., 2014; Picard et al., 2012).
Los modelos de mejor ajuste se seleccionaron con base en lo siguiente: a) mayores coeficientes de determinación (R2 y R2 ajustado) y b) un coeficiente de información de Akaike (AIC), un coeficiente bayesiano de información y una raíz del cuadrado medio del error (RCME) menores (Andrade et al., 2018; Picard et al., 2012; Segura & Andrade, 2008). Los análisis estadísticos se desarrollaron en Infostat©. Asimismo, se siguieron las recomendaciones de Cifuentes-Jara et al. (2014) para el reporte de ecuaciones alométricas y se estudiaron los gráficos de dispersión de residuos para ver posibles problemas de sesgo y heterocedasticidad, así como la lógica biológica del modelo, tal como recomiendan Andrade et al. (2014) y Segura y Andrade (2008).
Los mejores modelos se compararon con otros desarrollados en otros sitios, como los de Brahma et al. (2017) para H. brasiliensis en India, basados en el diámetro del tronco a 2 m de altura (Ecuaciones 1 y 5); los de Monroy-Rivera y Návar-Cháidez (2004) (Ecuación 2); los de Moreno et al. (2005) para Colombia (Ecuaciones 3 y 6); y los de Sone et al. (2014) en Sumatra (Ecuaciones 4 y 7):
Ba = exp(-3.31+0.95*Ln(dap2*at)) * 1.02 Ec. 1
B a = −548.448+0.008684*dap 2 * at
+ 27.48 * at +6.949 * dap Ec. 2
B a = 0.0041 * cap 2.596Ec. 3
B a = 0.144 * dap 2.40Ec. 4
B b = exp (-2.64+0,60*Ln(dap2*at)) * 1.04 Ec. 5
B b = 0.0022 * cap 2.357Ec. 6
B b = 0.0661 * dap 2.02Ec. 7
Donde:
B a : biomasa aérea (kg.árbol-1); B b : biomasa subterránea (kg.árbol-1); dap: diámetro a la altura del pecho (cm); at: altura total (m); y cap: circunferencia del tronco a la altura del pecho (cm).
Los estimados de los mejores modelos obtenidos en este estudio y de los modelos de referencia se compararon mediante el error relativo medio, método propuesto por van Breugel et al. (2011).
RESULTADOS
Características de los árboles muestreados
La B a de los árboles de H. brasiliensis varió entre 0.1 kg.árbol-1 y 1.8 Mg.árbol-1, en contraste con valores entre 0.3 y 181.7 kg.árbol-1 para los individuos de T. grandiflorum (Figura 2). La B b de esos árboles muestreados varió de 0.18 a 327.9 kg.árbol-1 en H. brasiliensis y de 0.09 a 21.0 kg.árbol-1 en T. grandiflorum (Figura 2), lo cual arroja relaciones B b /B a de 0.38 ± 0.1 y 0.10 ± 0.01, respectivamente. En H. brasiliensis se observa la típica curva de reducción de la B b /B a a medida en que crecen los árboles (de 1.5 a 0.2), tendencia que no fue detectada en T. grandiflorum (Figura 3).
Correlación entre variables
Se encontró que las variables dasométricas que mejor explicaron la B a y B b fueron el DAP en H. brasiliensis y el D30 en T. grandiflorum, con coeficientes de correlación de Pearson entre 0.89 y 0.94 (Figura 2). La AC también presenta un gran poder de explicación de B a y B b , al presentar coeficientes de correlación de Pearson de 0.85 a 0.95, siendo levemente superior el de H. brasiliensis. La AT y la AB no se correlacionaron bien con la biomasa, con valores de r entre -0.12 y 0.31 (Figura 2). Estos resultados indican que la B a y B b se pueden estimar en función del diámetro del tronco y de la AC.
Modelos de mejor ajuste
Los modelos de mejor ajuste explicaron la variabilidad de la biomasa entre un 84 y 97 %, siendo más exactos para aquellos para H. brasiliensis que los desarrollados para T. grandiflorum (Tabla 1). Los mejores modelos se basaron en el diámetro del tronco y, en todos los casos, la inclusión de la AT como segunda variable independiente no mejoró el ajuste del modelo, reduciéndolo incluso en algunos casos. De la misma manera, se presentó un muy buen ajuste de aquellos modelos alométricos que estiman la B a y B b en función del AC de los árboles (0.91< R2< 0.95).
A pesar de los adecuados estadígrafos de ajuste, el análisis de residuos permitió observar sesgos y problemas de heterocedasticidad en tamaños grandes de los árboles de H. brasiliensis. Así, se definieron los rangos de tamaño donde es recomendable aplicar los modelos por medio de curvas continuas en cada uno de los gráficos (Figura 4). Aunque las curvas punteadas son la estimación con los modelos generados, no es recomendable aplicarlos a esos tamaños de árboles, debido principalmente a problemas de sesgo. No se detectaron problemas de heterocedasticidad ni de lógica biológica en los modelos desarrollados en los rangos recomendados ni en los árboles de T. grandiflorum (Figura 5).
La comparación de los estimados con los otros desarrollados para H. brasiliensis permitió verificar el ajuste de dichos modelos y la ventaja de su aplicación en los sistemas de producción de caucho del Caquetá, Colombia. En el caso de la B a , el modelo de mejor ajuste desarrollado en el estudio (Figura 6) presentó un error relativo medio de 33 %, en comparación con los valores entre 39 y 55 % encontrados en los estimados realizados con los modelos de Brahma et al. (2017), Monroy-Rivera y Návar-Cháidez (2004), Moreno et al. (2005) y Sone et al. (2014). Entretanto, el modelo generado en este estudio para estimar la B b presentó una mayor exactitud, con un error relativo medio del 20 %, menor que los errores de las estimaciones con los otros modelos, cuyos errores son del 22 al 52 % (Figura 5) (Brahma et al., 2017; Moreno et al., 2005; Sone et al., 2014).

Figura 2 Correlación entre la biomasa aérea (B a ) y subterránea (B b ) y el diámetro del tronco (DAP: diámetro a la altura del pecho; D30: diámetro a 30 cm de altura), la altura a la base de la copa (AB), la altura total (AT) y el área de la copa (AC) en Hevea brasiliensis y Theobroma grandiflorum en el departamento del Caquetá, Colombia.
Tabla 1 Modelos de mejor ajuste para la estimación de la biomasa aérea y subterránea de árboles individuales de Hevea brasiliensis y Theobroma grandiflorum en el departamento del Caquetá, Colombia.
| Modelo | R2 | R2aj | AIC | BIC | RCME |
|---|---|---|---|---|---|
| Hevea brasiliensis | |||||
| Biomasa aérea | |||||
| Ln(B a )=-2.99+2.72*Ln(DAP) | 0.97 | 0.97 | 55.3 | 60.5 | 0.44 |
| Ln(B a )=-3.09+2.532*Ln(DAP)+0.262*Ln(AT) | 0.97 | 0.97 | 55.8 | 62.7 | 0.43 |
| Ln(B a )=0.144+1.508*Ln(AC) | 0.91 | 0.91 | 98.4 | 104.0 | 0.75 |
| Biomasa subterránea | |||||
| Ln(B b )=-3.09+2.22*Ln(DAP) | 0.99 | 0.99 | 6.85 | 9.68 | 0.25 |
| Ln(B b )=-3.123+2.13*Ln(DAP)+0.119*Ln(AT) | 0.99 | 0.99 | 8.11 | 11.9 | 0.24 |
| Ln(B b )=-0.599+1.191*Ln(AC) | 0.94 | 0.93 | 37.00 | 39.9 | 0.55 |
| Theobroma grandiflorum | |||||
| Biomasa aérea | |||||
| Ln(B a )=-2.59+2.48*Ln(D30) | 0.84 | 0.84 | 96.0 | 101.0 | 0.75 |
| Ln(B a )=-2.865+2.135*Ln(D30)+0.654*Ln(AT) | 0.86 | 0.86 | 92.8 | 99.5 | 0.70 |
| Ln(B a )=-0.741+1.408*Ln(AC) | 0.95 | 0.94 | 53.4 | 58.5 | 0.44 |
| Biomasa subterránea | |||||
| Ln(B b )=-3.92+2.07*Ln(D30) | 0.88 | 0.87 | 27.9 | 29.4 | 0.60 |
| Ln(B b )=-3.977+2.045*Ln(D30)+0.0063*Ln(AT) | 0.88 | 0.86 | 29.9 | 31.8 | 0.60 |
| Ln(B b )=-3.21+1.46*Ln(AC) | 0.95 | 0.95 | 16.9 | 18.3 | 0.38 |
B a : biomasa aérea (kg.árbol-1); B b : biomasa subterránea (kg.árbol-1); DAP: diámetro a la altura del pecho (cm); D30: diámetro del tronco a 30 cm de altura (cm); AT: altura total (m); AC: área de copa (m2); R2: coeficiente de determinación; R2aj: R2 ajustado; AIC: coeficiente de información de Akaike; BIC: coeficiente bayesiano de información; RCME: raíz del cuadrado medio del error.

Figura 3 Relación entre el diámetro del tronco (a la altura del pecho, DAP, y a 30 cm de altura, D30) y la relación biomasa subterránea/biomasa aérea (B b /B a ) en árboles individuales de Hevea brasiliensis y Theobroma grandiflorum en el departamento del Caquetá, Colombia.

Figura 4 Modelos de mejor ajuste y sus correspondientes figuras de residuos para la estimación de la biomasa aérea y subterránea con base en el diámetro del tronco a la altura del pecho y área de la copa de árboles individuales de Hevea brasiliensis en el departamento del Caquetá, Colombia. B a : biomasa aérea; B b : biomasa subterránea; DAP: diámetro del tronco a la altura del pecho; AC: área de la copa. Las líneas continuas representan el rango de biomasa donde se recomienda la aplicación de los modelos desarrollados.
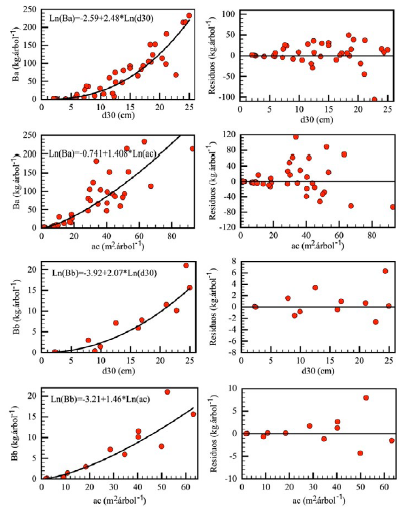
Figura 5 Modelos de mejor ajuste y sus correspondientes figuras de residuos para la estimación de la biomasa aérea y subterránea con base en el diámetro del tronco a 30 cm de altura y el área de la copa de árboles individuales de Theobroma grandiflorum en el departamento del Caquetá, Colombia. B a : Biomasa aérea; B b : biomasa subterránea; D30: diámetro del tronco a 30 cm de altura; AC: área de la copa.

Figura 6 Comparación de los estimados de los modelos de mejor ajuste para la estimación de la biomasa aérea y subterránea de árboles individuales de Hevea brasiliensis en el departamento del Caquetá, Colombia, y los recomendados por Brahma et al. (2017) (Ec. 1: B a = exp (−3.31+0.95∗Ln dap 2 ∗at ) ∗1.02 y Ec. 5: 𝐵 𝑏 = 𝑒𝑥𝑝 (−2.64+0.60∗𝐿𝑛 𝑑𝑎𝑝 2 ∗𝑎𝑡 ) ∗1.04), de Monroy-Rivera y Návar-Cháidez (2004) (Ec. 2: 𝐵 𝑎 =−548.448+0.008684∗ 𝑑𝑎𝑝 2 ∗𝑎𝑡+27.48∗𝑎𝑡+6.949∗𝑑𝑎𝑝), de Moreno et al. (2005) (Ec. 3: 𝐵 𝑎 =0.0041∗ 𝑐𝑎𝑝 2.596 y Ec. 6: 𝐵 𝑏 =0.0022∗ 𝑐𝑎𝑝 2.357 ) y de Sone et al. (2014) (Ec. 4: 𝐵 𝑎 =0.144∗ 𝑑𝑎𝑝 2.40 y Ec. 7: 𝐵 𝑏 =0.0661∗ 𝑑𝑎𝑝 2.02 ). B a : biomasa aérea (kg.árbol-1); B b : biomasa subterránea (kg.árbol-1); DAP: diámetro a la altura del pecho (cm); AT: altura total (m); CAP: circunferencia del tronco a la altura del pecho (cm). Las líneas continúan representan el rango de biomasa donde se recomienda la aplicación de los modelos desarrollados.
DISCUSIÓN
Relación B b /B a. La relación encontrada se convierte en otra herramienta importante y útil para estimar la biomasa subterránea en H. brasiliensis, lo que permite incrementar los estimados de biomasa y carbono en ~38 %. Aunque la tendencia no fue tan clara en T. grandiflorum, la inclusión de ese componente de biomasa incrementa los estimados en ~10 %. Este tipo de herramientas es muy valioso pero muy escaso en la literatura científica (Cairns et al., 1997; Kuyah et al., 2012; Kalita et al., 2015; Magalhães, 2015; Magalhães & Seifert, 2015). Esta herramienta permite mejorar las estimaciones de biomasa y carbono con mínima inversión de recursos técnicos y financieros.
Modelos de biomasa. Las relaciones alométricas encontradas en este estudio ya han sido ampliamente descritas en diferentes estudios sobre otras especies (Andrade et al., 2018; Chave et al., 2005; Segura & Kanninen, 2005; Sione et al., 2019) y en modelos para H. brasiliensis (Brahma et al., 2017; Monroy-Rivera & Návar-Cháidez, 2004; Moreno et al., 2005; Sone et al., 2014). No se detectaron modelos de biomasa desarrollados previamente para árboles de T. grandiflorum, lo que demuestra la importancia de estos hallazgos. Las transformaciones logarítmicas son métodos ideales y usualmente empleados para lograr linealizar datos dispersos y generar modelos de biomasa (Andrade et al., 2018; Picard et al., 2012). Hay pocos o nulos modelos de biomasa basados en el área de la copa en la literatura científica, usualmente herramientas sencillas para estimar esta variable que emplean herramientas como fotografía aérea o imágenes de satélite de alta resolución (Anaya et al., 2009; Meyer et al., 2018).
Los modelos de mejor ajuste, además de presentar los mejores estadígrafos, también resultan ser los más prácticos porque emplean una sola variable a medir: el diámetro. Esto reduce sensiblemente el error en mediciones y estimaciones (Andrade et al., 2018; Segura & Kanninen, 2005). Los modelos que más se aproximan a las estimaciones de los presentes son los de Brahma et al. (2017), desarrollados en India para biomasa aérea, y los de Moreno et al. (2005) para la biomasa aérea y subterránea en Colombia. Sin embargo, siempre se recalca el uso de modelos locales (Álvarez et al., 2012; Andrade et al., 2014; IPCC, 2003), los cuales mejoran las estimaciones debido a que consideran las situaciones específicas en un área de estudio determinada. Esto reconfirma la importancia de desarrollar modelos locales para reducir las incertidumbres y la exactitud en las estimaciones de los créditos de carbono (Andrade et al., 2018; IPCC, 2013).
Es importante recalcar los rangos de aplicación de los modelos desarrollados en este artículo. Así, los modelos para H. brasiliensis deben usarse en árboles con DAP<45 cm y AC<150 m2, mientras que los modelos alométricos para T. grandiflorum deben emplearse en árboles con un D30 menor a 25 cm y un AC máximo de 80 m2. El uso de estos modelos en rangos de tamaño diferentes a los mencionados podría causar graves errores en las estimaciones por posibles sesgos.
CONCLUSIONES
La relación entre biomasa subterránea y biomasa aérea permite incluir el componente radicular, estimando la biomasa total y la exactitud en las estimaciones. El uso de esta herramienta mejora las estimaciones de los créditos de carbono con mínima inversión.
Los modelos alométricos que presentaron el mejor ajuste para estimar la biomasa aérea y subterránea de H. brasiliensis y T. grandiflorum mostraron los mejores estadígrafos (tal como R2>0.84) y menores errores relativos de estimación. Los mejores modelos resultaron ser aquellos en los cuales solo se incluye una variable independiente, ya sea el diámetro del tronco a la altura del pecho o el área de copa de los árboles, lo que demuestra su sencillez y facilidad de uso. El uso de área de copa para estimar la biomasa de estas dos especies representa una oportunidad para emplear sistemas de información geográfica que empleen fotografías aéreas o imágenes de satélite de alta resolución o el uso de drones. Sin embargo, debe profundizarse la investigación en este y otros sistemas agroforestales.
Se espera que estas herramientas sean útiles en investigación sobre carbono y ciclaje de nutrientes, así como en proyectos de carbono tal como aquellos orientados hacia mercados voluntarios y proyectos de reducción de emisiones por deforestación y degradación.















