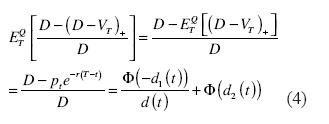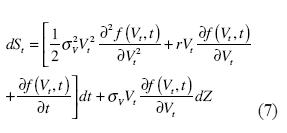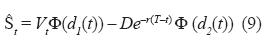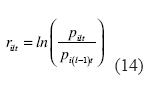Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Administración
Print version ISSN 0120-3592
Cuad. Adm. vol.24 no.42 Bogotá Jan./June 2011
* Este trabajo forma parte del proyecto de investigación Metodología para la medición del riesgo de crédito en empresas no financieras, que se desarrolla dentro del proyecto ECO2010-22065-C03-03: Modelos actuariales de medición y transferencia del riesgo: riesgo de crédito y riesgo de suscripción, financiado por el Gobierno de España - Ministerio de Ciencia e Innovación, la Universitat de Barcelona, España y la Universidad del Valle, Colombia. Nuestros agradecimientos a las entidades financiadoras del proyecto, a los evaluadores de este artículo y a Maite Mármol y Anna Castañer por los comentarios realizados a versiones previas. Todos los errores, comentarios y observaciones son de la absoluta y total responsabilidad de los autores y no comprometen en ningún sentido a las instituciones en las cuales laboran. El artículo se recibió el 09-09-10 y se aprobó el 13-05-11.
** Doctorando en Empresa de la Universitat de Barcelona, Barcelona, España; Master en Investigación en empresa, finanzas y seguros de la misma universidad, 2009; Magister en Ciencias de la organización, Universidad del Valle, Cali, Colombia, 1999 y Estadístico de la misma universidad colombiana, 1992. Profesor Asociado y miembro del Grupo de Investigación en solvencia y riesgo financiero, Departamento de Contabilidad y Finanzas, Facultad de Administración, Universidad del Valle, Cali, Colombia. Correo electrónico: edcaiced@hotmail.com.
*** Doctora en Economía y Empresa de la Universitat de Barcelona, Barcelona, España, 1992; Licenciada en Ciencias económicas y actuario en seguros de esta misma universidad, 1987. Profesora Titular de Universidad y miembro del Grup de Recerca en Teoria de Jocs, Investigació Operativa i Optimització (2009SGR960), Departament de Matemàtica Econòmica, Financera i Actuarial, Facultat d'Economia i Empresa, Universitat de Barcelona, Barcelona, España. Correo electrónico: mmclaramunt@ub.edu.
**** Doctora en Ciencias económicas y empresariales, Universidad Autónoma de Barcelona, Barcelona, España, 1977; European Financial Advisor, European Financial Planning Association, Barcelona, España, 2003; Análista Financiero, Instituto Español de Análistas Financieros, Madrid, España, 1980; Auditora financiera, Colegio de Economistas de Cataluña, Barcelona, España, 1977. Profesora Catedrática de Universidad y miembro del Grup de Recerca en Economia i Gestó de la Incertesa, Departament d'Economia i Organització d'Empreses, Facultat d'Economia i Empresa, a Universitat de Barcelona, España. Correo electrónico: mcasanovas@ub.edu.
RESUMEN
Este artículo presenta los resultados del estudio sobre medición del riesgo de crédito en firmas incluidas en el Índice General de la Bolsa de Valores de Colombia (IGBC) entre 2005 y 2007. Las probabilidades de incumplimiento y las tasas de recuperación dado el incumplimiento se estiman mediante el enfoque estructural de Merton y sus extensiones. Con los supuestos de volatilidad constante y heterocedástica de los activos de las firmas se obtienen estimaciones a nivel de empresas y sector económico. Los resultados indican, con una significación estadística del 1% y mediante la aplicación de pruebas no paramétricas, que en ese periodo no hubo diferencias significativas en la probabilidad de incumplimiento a nivel de sectores y que los patrones de heterocedasticidad considerados en la volatilidad de los activos no tienen incidencia significativa en la estimación de la probabilidad de incumplimiento.
Palabras clave: Probabilidades de incumplimiento, modelos estructurales, modelo de Merton, volatilidad de activos.
Clasificación JEL: G12, G21.
ABSTRACT
This article presents the results of the study on credit risk management in shares included in the Colombian stock exchange index (IGBC), between 2005 and 2007. The probability of default and rates of recovery given default are estimated using the Merton structural approach, and its extensions. The assumptions of constant volatility and heteroskedacity of the companies´ assets are used to provide estimates by individual company and by economic sector. The results indicate, with a statistical significance of 1%, and using non-parametric tests, that in that period there were significant differences in the probability of default at the level of the sector, and that the patterns of heteroskedacity considered in the volatility of assets have no significant influence on the estimates of the probability of default.
Keywords: Probability of default, structural models, Merton model, asset volatility.
JEL Classification: G12, G21.
RESUMO
Este artigo apresenta os resultados de uma pesquisa sobre a medição do risco de crédito em firmas incluídas no Índice Geral da Bolsa de Valores da Colômbia (IGBC) entre 2005 e 2007. As probabilidades de inadimplência e as taxas de recuperação dadas à inadimplência foram estimadas mediante o enfoque estrutural de Merton e suas extensões. Com os supostos de volatilidade constante e heterocedástica dos ativos das firmas obtêm-se estimativas no âmbito de empresas e setor econômico. Os resultados indicam, com uma significação estatística de 1% e mediante a aplicação de provas não paramétricas, que nesse período não houve diferenças significativas na probabilidade de inadimplência no âmbito de setores e que os padrões de heterocedasticidade considerados na volatilidade dos ativos não têm incidência significativa na estimativa da probabilidade de inadimplência.
Palavras chave: Probabilidades de inadimplência, modelos estruturais, modelo de Merton, volatilidade de ativos.
Classificação JEL: G12, G21.
Introducción
El riesgo de crédito se define como la pérdida potencial que se registra con motivo del incumplimiento de una contraparte en una transacción financiera (o en alguno de los términos y condiciones de la transacción) (De Lara, 2003). También se concibe como un deterioro en la calidad crediticia de la contraparte o en la garantía o colateral pactado originalmente.
Según Basilea I (1988) el riesgo de crédito se define como el riesgo de que la contraparte incumpla en la obligación. En Basilea II y en el proyecto de Solvencia ii no se encuentra una definición concreta sobre riesgo de crédito. Según la International Actuarial Association (2004) el riesgo de crédito se define como el riesgo a que una compañía está expuesta por el incumplimiento o impago de una obligación de crédito o por el cambio en la calidad en las garantías del crédito de la contraparte o de los intermediarios que inicialmente habían sido acordadas.
La crisis financiera que se reveló en el año 2007 y que se profundizó en los años 2008 y 2009, ratifica una vez más, y ha dejado de manifiesto, que la gestión del riesgo de crédito, específicamente su medición, es un tema de vital importancia para reguladores, directores de empresas e inversionistas, por los efectos sistemáticos que dicho riesgo puede ocasionar. Las técnicas de medición del riesgo de crédito incluyen modelos tradicionales, modelos estructurales y modelos de forma reducida (Jackson et al., 1999; Márquez, 2006).
Los modelos tradicionales comprenden: el modelo de las 5 Cs, el modelo de Altmant (1968 y 2000), Altman et al. (1977), Altmant et al. (1994), Altman y Sabato (2005) y el modelo estándar de Basilea (1988, 2001 y 2004).
Los modelos estructurales de amplio reconocimiento en los mercados financieros, utilizados por grandes firmas y de amplia divulgación en la literatura financiera, suponen que los inversores tienen toda la información del mercado y tienen un conocimiento completo del valor de los activos y la deudas de todas las firmas (Jarrow y Protter, 2004). Los modelos estructurales incluyen el modelo de Merton (1974), Geske (1977), el modelo CreditMetrics de JP Morgan and Company (1977) y el modelo CreditPortafolioMaganer de KMV Moody's. Una descripción de los modelos estructurales se presenta en Elizalde (2005) y su aplicación al mercado bursátil español con información del año 2003 se presenta en Samaniego et al. (2007). Pederson y Zech (2009) y Zech y Pederson (2004) los aplican en el sector agrícola canadiense. Seilder y Jakubik (2009) hacen una aplicación de los modelos estructurales en el cual estudian las implicaciones, en la República Checa, de las pérdidas dado el incumplimiento de las firmas.
Los modelos de forma reducida asumen que los inversores no disponen de toda la información sobre el manejo de la firma, y esta falta de conocimiento no permite predecir la probabilidad de incumplimiento de las firmas1. Entre los modelos de forma reducida más importantes se encuentra el modelo CreditPortafolioView de Mckinsey2. En esta categoría también están otros trabajos realizados por distintos autores que se basan en modelos logit, modelos probit, modelos lineales de probabilidad, simulación3, en redes neuronales artificiales4 y en metodología borrosa5.
Entre los trabajos que comparan los modelos estructurales con los modelos de forma reducida se encuentran: Jarrow y Protter (2004), Chen etal. (2008) y Aroraetal. (2005). Chen y Panjer (2003) relacionan los modelos estructurales con los de forma reducida consderando los valores observados del spread del mercado (premio al riesgo por la deuda riesgosa). Un modelo importante, que no se clasifica en ninguna de las tres categorías anteriores, que también es considerado como uno de los modelos estándares para la medición del riesgo de crédito, es el modelo CreditRisk+ de Credit Suisse Fiancial Products.
Los modelos de forma reducida suponen que la empresa cuenta con información a priori de sus clientes y los tiene clasificados como cumplidos o incumplidos en torno a las obligaciones que implica el crédito, y este incumplimiento se puede relacionar con variables internas y externas de sus clientes. En la revisión de la literatura financiera efectuada hasta el momento de escribir este documento, los modelos logit son los más frecuentemente usados.
Según Greene (2000), el mayor uso de los modelos logit se puede deber a la facilidad de aplicación, comprensión e interpretación de sus resultados. Sin embargo, al aplicar los modelos logit se parte de la clasificación de los clientes como cumplidos e incumplidos (default o no default). Lo que se ha observado es que, en empresas financieras, cuando se hace la aplicación de los modelos logit, la cantidad de clientes default no supera el 15% de los casos en las bases de datos6, lo que puede ocasionar un sesgo en el momento de la estimación del riesgo de crédito debido al peso que tienen los clientes no default en la estimación de la probabilidad de incumplimiento.
Dada la importancia que tiene el crédito en las actividades comerciales que realizan empresas del sector financiero y no financiero con sus clientes, es de vital relevancia encontrar respuesta a la pregunta: ¿cuál es la probabilidad que el cliente de una entidad financiera o no financiera, incumpla en el pago de una obligación que ha contraído con la misma entidad?
El objetivo de este documento es medir el riesgo de crédito de empresas que cotizan en bolsa de valores a través del modelo estructural de Merton (1974). En concreto, se analizan empresas que cotizaron sus acciones en el mercado colombiano durante el periodo 2005-2007. Además, es de interés en este trabajo analizar si hay diferencias en los indicadores de riesgo de crédito entre las empresas cuando se agrupan por sectores económicos.
La primera parte de este artículo se dedica a la introducción, la segunda consiste en un repaso a los modelos estructurales de medición de riesgo crédito, la tercera sección expone la metodología seguida en el estudio, y la cuarta presenta los resultados de la investigación. Finalmente, en la quinta sección se describen las conclusiones.
En la revisión de la literatura, efectuada hasta el momento de realizar la investigación, no se encontraron publicaciones que se orientaran a la medición del riesgo de crédito en empresas colombianas mediante la aplicación de modelos estructurales. Este artículo se constituye en la primera evidencia empírica para académicos, directores de empresas y autoridades a nivel nacional e internacional de la aplicación de modelos estructurales en la medición del riesgo de crédito en empresas colombianas.
1. Repaso a los modelos estructurales
1.1 El modelo de Merton (1974)
El modelo de Merton (1974) asume que: 1) el mercado es perfecto y libre de fricciones, es decir, muchos inversores pueden vender al descubierto y comprar más de lo que ellos poseen en tiempo continuo; 2) la estructura de términos de las tasas de interés es plana, y la tasa de interés es fija para prestatarios y prestamistas en todo momento; 3) el valor de la firma es invariante a su estructura de capital; 4) una empresa se puede financiar con capital propio y deuda (D) que vence en el tiempo t, tanto el capital propio como la deuda se transan en el mercado; 5) todas las variables aleatorias se pueden definir en un espacio de probabilidad (Α, F,F,t Q), en el cual q representa una media de probabilidad en condiciones de incertidumbrey 6) el valor de los activos de la firma, Vt, en el momento t, es transado en el mercado y sigue un proceso difuso dado por:
dVt= (aVt + c) dt + σvVtdZt
donde σV 2 es la varianza instantánea de Vt, es la tasa de retorno instantánea, c es el total de pagos incluyendo dividendos y cupones, y Zt sigue un movimiento browniano.
Merton (1974) sugiere que un derivado del valor de los activos de la firma, C (Vt ,t) , podría seguir otro proceso difuso. Bajo condiciones de no riesgo y de no arbitraje, la tasa de retorno instantánea podría considerarse como la tasa libre de riesgo r y C (Vt ,t) sigue el siguiente proceso:
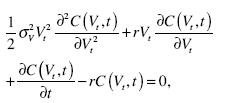
con la condición de contorno C (x,T) = g(x) para un pago g(x) del derivado al vencimiento t.
Si se considera que el valor de mercado de la deuda y el capital propio son unos derivados del valor de los activos de la firma que satisfacen la ecuación anterior, entonces el valor de la firma en el momento t está dado por:

donde V (t,T) es valor de mercado de la deuda por cada unidad monetaria de valor nominal.
El valor del capital propio de la firma en el momento t, St, viene dado por el precio de una opción call europea sobre el valor de los activos de la firma. Black y Scholes (1973) muestran que:

y
siendo (Φ) la función de distribución de una ~N(0,1) y σV 2 , r, Vt y D como fueron definidas anteriormente. El valor de mercado de la deuda por cada unidad monetaria de valor nominal, V(t,T) es:

1.1.1 Estimación de la probabilidad de incumplimiento
Según Merton (1974), un incumplimiento sólo puede ocurrir al vencimiento de la deuda, y ocurre solamente si el valor de la firma en el momento T, VT se sitúa por debajo de la deuda (D).
El valor de la razón VT / D determina o no el incumplimiento. Si VT / D > 1 el incumplimiento no sucede. Si VT / D < 1 el incumplimiento se presenta, y la razón VT / D representa la tasa de recuperación.
En el modelo de Merton (1974), lnVT sigue una distribución normal con media 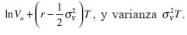
Asumiendo que la compañía ha sobrevivido t años y el tiempo en que se presenta el incumplimiento es una variable aleatoria que se denota como τt, entonces en t, la probabilidad de que se presente el incumplimiento en el momento t es:
y la probabilidad de que no se presente el incumplimiento en el momento t, es la complementaria7:

Al considerar la tasa libre de riesgo, r, en (1), (2) nos da una estimación de probabilidad neutral de incumplimiento. Para obtener la probabilidad de incumplimiento de la firma se remplaza en (1) la tasa libre de riesgo, r, por la tasa de crecimiento de los activos de la empresa, µ (Löffler y Posch, 2007); d2(t) viene dado entonces por8:
Según Löffler y Posch (2007) y Vassalou y Xong (2004), d2(t) estimada como se presenta en (3), es denominada la distancia al default y se interpreta como el número de desviación estándar en que se debe disminuir el logaritmo natural de la ratio Vt D de su media para que se produzca el incumplimiento de la firma.
1.1.2 Estimación de la tasa de recuperación dado el incumplimiento
Denotamos por δ(T) a la tasa de recuperación dado el incumplimiento. Esta tasa de recuperación es la proporción que representa VT sobre D si la firma incumple en el momento T. Siguiendo a Chen y Panjer (2003), su función de distribución es:


donde pt es el precio en el momento t de una opción de venta (put) tipo europea sobre el valor de los activos de la firma. Este valor esperado en (4), puede ser escrito como sigue:

Luego, el valor esperado de la tasa de recuperación dado el incumplimiento puede ser expresado, en términos del valor esperado de la proporción que el prestamista recibiría en el momento T, de la siguiente forma:

Chen y Panjer (2003) basándose en la paridad put call, muestran que la tasa de recuperación obtenida del modelo de Merton (1974) se puede expresar en términos del valor del capital propio en el momento t, St, de la siguiente forma:

1.2 Modelo CreditPortfolioManager de KMV Moody's
Este modelo aplica la teoría de las opciones para determinar las probabilidades de incumplimiento y la evaluación del préstamo, y es también conocido como modelo Credit Monitor (CM). Calcula las probabilidades de incumplimiento de cada deudor a través del modelo de Merton (1974). Estas probabilidades son función de la estructura de capital, la volatilidad de los retornos y el valor de los activos9.
Se basa en la distancia al default (d2(t)), como una medida intermedia a la probabilidad de incumplimiento, y en que el incumplimiento se presenta cuando el valor de los activos de la empresa cae por debajo de un umbral que está definido entre el valor de los pasivos totales y la deuda de corto plazo. Con la distancia al default determina las probabilidades de incumplimiento ((-d2(t)) y calcula las clasificaciones, construye las matrices de transición y estima la distribución de las pérdidas esperadas del portafolio.
1.3 El modelo CreditMetrics de JP Morgan
CreditMetrics desarrolla el modelo de riesgo de crédito a través de las siguientes etapas: 1) especifica un sistema de calificaciones y una matriz de transición utilizando la información de las agencias calificadoras (Moody's o Standard and Poor's); 2) establece un horizonte de tiempo que por lo general es de un año; 3) desarrolla un modelo de valoración; 4) analiza los cambios en el valor de la cartera de créditos; y 5) define el incumplimiento como el momento en el cual el valor de los activos se encuentra por debajo del valor nominal de los créditos10.
1.4 El modelo Geske (1977)
El modelo de Geske (1977) utiliza el modelo de Merton (1974), pero se basa en que el valor de los activos es una opción compuesta. En este marco los deudores tienen una opción compuesta donde la opción de impago del presente cupón (deuda de largo plazo) existe sólo si la corporación no ha fallado el pago del cupón previo (deuda de corto plazo). Permite entonces, una estructura de capital más realista con deuda a corto plazo, pagos de cupones, deuda subordinada, fondos de amortización y otros compromisos de pago. Sin embargo, el modelo de Geske (1977) requiere contar con información detallada de los vencimientos de la deuda de corto y largo plazo de la compañía.
1.5 Diferencias conceptuales de los modelos presentados
No es un objetivo en esta investigación hacer un análisis comparativo de los modelos de riesgo de crédito. Un análisis de esta naturaleza se realiza en Crouhy et al. (2000) y en Saveedra y Saveedra (2010). Sin embargo, en esta sección se mencionan algunas diferencias conceptuales y se hacen algunos comentarios sobre los modelos presentados anteriormente.
Se puede observar que el modelo de Merton (1974) es la base para los cálculos de las probabilidades de incumplimiento en el modelo de KMV Moddy's y del modelo de Geske (1977). Sin embargo, en el modelo de Merton (1974) el incumplimiento se presenta cuando el valor de los activos es inferior al monto total de la deuda financiera, mientras que en el modelo de KMV Moddy's el incumplimiento se presenta cuando el valor de los activos está por debajo de un umbral definido entre los pasivos totales y la deuda de corto plazo. Esta diferencia en el establecimiento del umbral afecta directamente la probabilidad de incumplimiento, pues manteniendo los demás factores constantes, mientras más alejado se ubique el umbral del monto total de la deuda menor será la probabilidad de incumplimiento.
En el modelo de Geske (1997) se considera que el valor de los activos de la firma es una opción compuesta determinada por los montos y vencimientos de las deudas de corto y largo plazo de la compañía, mientras que en el modelo de Merton (1974) el valor de los activos seconsideracomouna call con precio de ejercicio el monto de la deuda. Considerar que el valor de los activos de la firma sigue una opción compuesta demanda información específica sobre la estructura de vencimiento de la deuda; con esta información a través del modelo de Geske (1997) se pueden estimar tres indicadores de probabilidad de incumplimiento para una firma: la probabilidad conjunta que se incumplan las deudas de corto y largo plazo, la probabilidad que se incumpla la deuda de corto plazo y la probabilidad que se incumpla la deuda de largo plazo dado que se ha cumplido con el pago de la deuda de corto plazo.
La principal crítica que ha recibido el modelo de Merton (1974) es que los spread (premio al riesgo por la deuda riesgosa) que se estiman a través del modelo son muy bajos en comparación con los que se dan en la práctica. Chen y Panjer (2003) deducen que el spread estimado a través del modelo de Merton (1974) es equivalente al spread obtenido en los modelos de forma reducida, por esta razón podrían usarse la información de los spread del mercado para llegar a estimaciones de la probabilidades de incumplimiento ajustadas a la información de los spread del mercado. Hay que anotar que los spread de mercado considerados en Chen y Panjer (2003) son dados por las agencias calificadores como Moddy's que se basan en las calificaciones obtenidas de las matrices de transición y estas se establecen con las probabilidades de incumplimiento calculadas a través del modelo de Merton (1974).
En la sección 1.3 se mencionó que el modelo CreditMetrics utiliza información de las agencias calificadoras (p. ej. Moody's o Standard and Poor's). Esta dependencia de la información histórica de las agencias calificadoras presenta un inconveniente el cual radica en que las probabilidades de incumplimiento actuales sean iguales al promedio de las probabilidades de incumplimiento de la compañía calculada con datos históricos. Otro inconveniente que presenta el modelo CreditMetrics es que supone que todas las compañías calificadas en una misma categoría presentan la misma probabilidad de incumplimiento.
2. Metodología
2.1 Estimaciones de las probabilidades de incumplimiento y las tasas de recuperación
Para la estimación de las probabilidades de incumplimiento y las tasas de recuperación se emplea el modelo de Merton (1974) que se presentó en la sección 1. Este modelo fue elegido debido exclusivamente a la disponibilidad de la información para las empresas analizadas.
Otros modelos requieren de información específica para las empresas que no estaba disponible en esta investigación. Por ejemplo, en el modelo de Geske (1977) se considera que se tiene información sobre los vencimientos de la deuda a corto y a largo plazo de la empresa; por lo menos esto supone conocer la estructura de vencimiento de la deuda de las compañías, información no disponible en este trabajo. Igual ocurre con la información requerida para la aplicación de las extensiones que proponen Chen y Panjer (2003). La aplicación de modelos de forma reducida, específicamente la utilización de un modelo probit o logit considera tener información a priori de las compañías clasificadas como cumplidas o incumplidas. La utilización de modelos que partan de una clasificación a priori de las compañías no es de interés para esta investigación, pues nos interesa estimar la probabilidad de incumplimiento de compañías suponiendo que sólo tenemos información de mercado.
Para la aplicación del modelo de Merton (1974) consideramos que un préstamo a una compañía se puede describir a través del perfil de una call (opción de compra) tipo europea, donde el emisor es el prestamista y el comprador son los accionistas de la compañía. El valor de la call, que representa el valor de capital propio, tiene como subyacente el valor de los activos de la firma y como precio de ejercicio el monto de la deuda financiera de la compañía. Por lo tanto, se requiere de las estimaciones del valor de los activos de la firma, Vt y su volatilidad, σv .
En la literatura financiera se describen diferentes métodos para estimar los valores de Vt y σv. Por ejemplo, Löffler y Posch (2007) presentan un método iterativo basado en el comportamiento histórico del valor del capital propio y el valor nominal de la deuda en libros en un año de ejercicio; Ericsson y Reneby (2005) proponen un método de estimadores de máxima verosimilitud basado en el valor observado del capital propio; Duan y Fulop (2009) usan el método de la máxima verosimilitud considerando que el valor del capital propio puede estar influenciado por el ruido de las transacciones.
Jones et al. (1984) proponen dos métodos para estimar la volatilidad del valor de los activos de la firma. El primer método se basa en una serie histórica del valor de los activos de la firma, el cual puede estimarse a través del valor de mercado del capital propio, el valor de mercado de la deuda que es transada en el mercado y el valor en libro de la deuda que no se transa en el mercado. El segundo método, que es el que se emplea en este estudio, hace uso del Lemma de Itô, del cual se obtiene un sistemas de dos ecuaciones en el que solamente las variables Vt y σv son desconocidas. Se asume que el valor del capital propio St, sigue un proceso de Gaus-Winner con volatilidad σS:
donde σS es la desviación estándar, a es la tasa de retorno instantánea y Zt sigue un movimiento browniano.
Por otro lado, el valor del capital propio es función del tiempo y del valor de los activos de la firma, St = f (Vt,t). Aplicando el Lemma de Itô se tiene que:
De la comparación de los coeficientes del proceso de Gaus-Winner en (6) y (7), se tiene la primera ecuación dada por:
La segunda ecuación resulta de comparar el valor observado del mercado de St, t, con su valor teórico, es decir:
De esta manera, el sistema de dos ecuaciones en el cual solamente las variables Vt y v son desconocidas es:
Para resolver (10) y estimar los valores de Vt y sV, se necesita tener las estimaciones del valor observado del mercado del capital propio, St y de la volatilidad de los retornos del capital propio, sS. St se calcula como:
donde ∆it es el número de acciones en circulación de la compañía i, al final del año t y Pit es el precio de cierre de la acción i en el año t.
La volatilidad de los retornos diarios del capital propio de la compañía i en el año t,  se estimó a través de la desviación estándar y la volatilidad histórica de los retornos de la acción como se presentan en las ecuaciones (12) y (13) respectivamente11.
se estimó a través de la desviación estándar y la volatilidad histórica de los retornos de la acción como se presentan en las ecuaciones (12) y (13) respectivamente11.
donde ritl es el retorno diario continuo de la acción i el día l del año t, y está dado por:
siendo pitl el precio de cierre de la acción i el día 1 del año t.
Al considerar la volatilidad histórica de los retornos del capital propio se tiene en cuenta los patrones heterocedásticos de los retornos del capital propio. Dada la importancia que representa la volatilidad del capital en la estimación del valor de los activos de la firma y de la volatilidad de dichos activos, es de interés en esta investigación validar si hay diferencias significativas entre la volatilidad del capital propio estimada con desviación estándar, y la estimada a través de la volatilidad histórica.
Como se ha presentado en este artículo cuando se emplea el modelo de Merton (1974) se pueden tener estimaciones de la probabilidad neutral de incumplimiento y de la probabilidad de incumplimiento de la compañía; la primera se obtiene cuando se considera la tasa libre de riesgo (ecuación (1)) y la segunda cuando se emplea la tasa de crecimiento de los activos de la compañía (ecuación (3)) la cual se ha aproximado mediante la tasa del crecimiento del PIB. Es de interés en este trabajo validar si hay diferencias entre las probabilidades neutrales de incumplimiento y las probabilidades de incumplimiento de las compañías.
2.2 Datos, fuentes y procesamiento de la información
El estudio incluye empresas que cotizaron en el mercado colombiano durante el periodo 2005-200712. Durante ese lapso de tiempo se reconoce el periodo expansivo de la economía colombiana lo cual se ve reflejado en el incremento del PIB del país, evitando de esta manera los efectos exógenos que podría ocasionar en la estimación de las probabilidades de incumplimiento la inclusión de periodos de crisis financiera que comenzó a reconocerse en la literatura financiera a partir de 2008.
En el cuadro 1 se presentan el número de empresas incluidas y la distribución de las empresas por sectores económicos.

La información de balances y estados de resultados corresponde a la Superintendencia Financiera de Colombia. La información sobre precios y acciones en circulación fue obtenida de la Bolsa de Valores de Colombia (cuadro 2).

Se seleccionaron las compañías que presentaron alta bursatilidad por ser las que con mayor frecuencia transaron sus acciones en el mercado de valores colombiano. Las compañías así seleccionadas pertenecieron al Índice General de la Bolsa de Valores de Colombia durante el periodo de análisis. La frecuencia de la información de balances y estados de resultados y número de acciones en circulación es anual; la frecuencia de información de los precios de las acciones es diaria. Las variables consideradas para cada compañía se presentan en el cuadro 3. El procesamiento de los datos se efectuó con Mathematica 6.0, SPSS, Excel y R.

3. Resultados y discusión
3.1 Variables determinantes de la probabilidad de incumplimiento
Para estimar las probabilidades de incumplimiento según el modelo de Merton (1974), siguiendo las expresiones (2) y (3) se necesita: la tasa libre de riesgo (r), la tasa de crecimiento de los activos de la empresa (µ) (para la cual hemos tomado como proxy el crecimiento del PIB), el valor nominal en libros de la deuda (D), el tiempo al vencimiento de la deuda (T), el valor del capital propio (St) y la volatilidad del capital propio (σS). En el cuadro 4 se muestran los valores promedios de las variables mencionadas.

Durante el periodo de estudio se puede apreciar una relación positiva entre la tasa libre de riesgo y la tasa de crecimiento del PIB. Es decir, en la medida en que se incrementó el PIB durante el periodo 2005-2006 también se incrementó la tasa libre de riesgo.
Al considerar la tasa del crecimiento del PIB como una proxy de la tasa de crecimiento de la empresa, manteniendo los otros factores constantes, lo que podría esperarse es que las probabilidades de incumplimiento de las compañías consideradas en el estudio disminuyeran del año 2005 a 2007, ya que la tasa de crecimiento del PIB aumenta en dicho periodo.
En la medida en que se presentó una mayor capitalización bursátil también se incrementó el endeudamiento de las empresas consideras en el estudio. La volatilidad del capital propio disminuyó a una tasa del 13,10% desde el año 2005 al 2007, lo cual indica que el riesgo total que asumieron los tenedores de las acciones disminuyó durante el periodo de estudio, y las empresas del sector financiero que otorgaron deuda a estas empresas experimentaron una probabilidad incumplimiento menor del año 2005 a 2007.
En el cuadro 4 se observa que la volatilidad del capital propio estimada con la desviación estándar es muy similar a la estimada con la volatilidad histórica; la prueba de rango de Wilcoxon13 nos permite validar de una manera más objetiva la igualdad de dichas estimaciones (cuadro 5).

A un nivel de significancia del 1%, no existe la suficiente evidencia para rechazar la hipótesis que en los años 2005, 2006 y 2007 la volatilidad del capital propio estimada con la desviación estándar de sus rendimientos, es igual a la volatilidad del capital propio estimada a través de la volatilidad histórica de los mismos rendimientos del capital propio. Razón por la cual en adelante se presenta los resultados obtenidos con la volatilidad del capital propio estimada con la desviación estándar de sus rendimientos.
3.2 Estimación del valor y la volatilidad de los activos
Calculada la desviación estándar del capital propio a partir de las ecuaciones (12) y (13), se estima el valor de los activos de la firma, Vt y su volatilidad, σV del sistema de ecuaciones (10).
En los resultados del cuadro 6 se aprecia una correlación negativa entre el valor de los activos de las firmas y su volatilidad, lo cual indica que entre el 2005 y el 2007 a medida que se incrementó el valor de los activos de las empresas incluidas en el análisis, se disminuyó su volatilidad, lo cual también indica que las empresas del sector financiero que otorgaron deuda a estas empresas experimentaron una probabilidad de incumplimiento menor de 2005 a 2007. Debe tenerse en cuenta que, para cada compañía incluida en el análisis, el valor estimado de sus activos (obtenido a través de la solución del sistema de ecuaciones (10)) es función del valor de la deuda en libros de la firma. El número de empresas analizadas son 17 en el año 2006, 20 en 2006 y 25 en 2007 y, como se puede apreciar en el anexo 1, de las empresas analizadas en 2007, específicamente Isagen, etb y Ecopetrol presentan un componente alto en el valor de la deuda lo que ocasiona un monto elevado en la estimación del valor de sus activos y, por tanto, del promedio de las empresas consideradas en ese año.
Considerando que no se presentaron diferencias significativas en la volatilidad del capital propio estimada con la desviación estándar de los rendimientos y la estimada con la volatilidad histórica, en el cuadro 6 se presentan las estimaciones del valor de los activos y la volatilidad de los activos obtenidas con las estimaciones de la volatilidad del capital propio calculadas mediante la desviación estándar.

3.3 Probabilidades de incumplimiento y tasas de recuperación por empresa
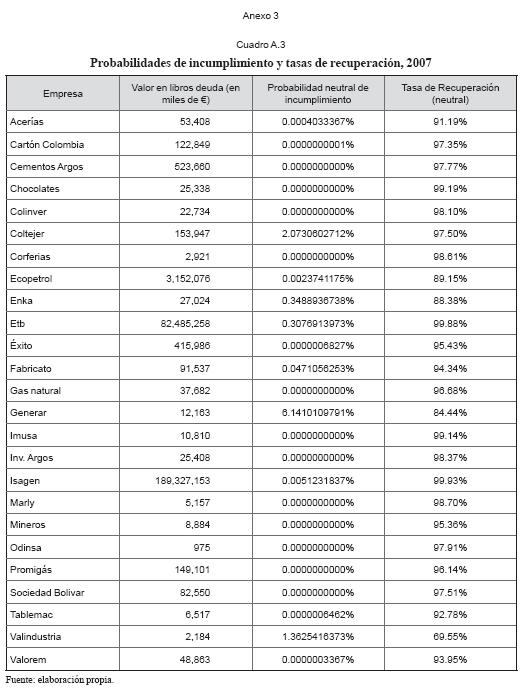
Con las estimaciones del valor de los activos con sus correspondientes volatilidades, los niveles de la tasa libre de riesgo, el crecimiento de los activos de la empresa y el nivel de la deuda financiera en libros, se estiman las probabilidades neutrales de incumplimiento, las probabilidades de incumplimiento y las tasas de recuperación dado el incumplimiento para cada empresa como se muestran en los anexos 1, 2 y 3 para los años 2005, 2006 y 2007 respectivamente. En el cuadro 7 se presentan las estadísticas básicas de las probabilidades de incumplimiento y las tasas de recuperación dado el incumplimiento para cada año del periodo analizado.
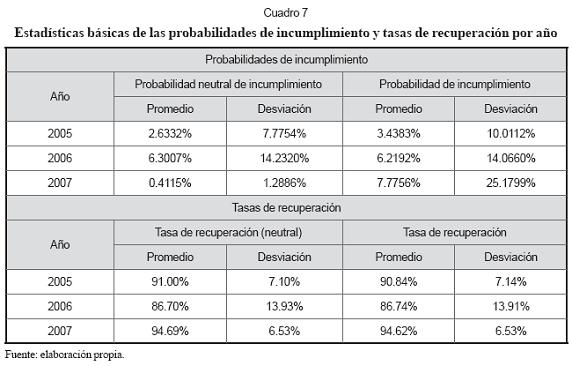
Debe tenerse en cuenta que para calcular la probabilidad de incumplimiento de la firma se ha remplazado la tasa la libre de riesgo por la tasa de crecimiento del PIB. Este cambio, como se puede observar en el cuadro 7, produce un incremento notable en la probabilidad de incumplimiento comparada con la probabilidad neutral de incumplimiento en el año 2007.
La probabilidad de incumplimiento de una compañía está determinada por la distancia al incumplimiento (3).
 siempre valores mayores que cero, por lo cual ante crecimientos (o disminución) de la tasa de crecimiento de la empresa, el valor de la distancia al d2(t) se incrementa (disminuye). Por otro lado, de la ecuación (2) se tiene que la derivada parcial de σ(-d2(t)) con respecto a µ:
siempre valores mayores que cero, por lo cual ante crecimientos (o disminución) de la tasa de crecimiento de la empresa, el valor de la distancia al d2(t) se incrementa (disminuye). Por otro lado, de la ecuación (2) se tiene que la derivada parcial de σ(-d2(t)) con respecto a µ:

toma siempre valores menores que cero, por lo cual la probabilidad de incumplimiento de la empresa disminuye cuando se incrementa µ, y aumenta cuando disminuye.
Ahora ¿qué tan grande es el efecto de una variación en la tasa de crecimiento de la empresa, en la probabilidad de incumplimiento? Fijadas T, t y σV, el efecto depende del valor inicial de la distancia al incumplimiento d2(t). Recordando que la probabilidad de incumplimiento de una compañía está dada por Α(d2(t)), entonces mientras más alejada esté d2(t) de cero menor va a ser el efecto de un cambio en la tasa de crecimiento de la compañía sobre la probabilidad de incumplimiento de la misma. Este razonamiento podría ser una explicación del porque la tasa de crecimiento de una compañía, contrario a lo planteado por Crosbie y Bohn (2003), sí podría tener un efecto discriminante en la probabilidad de incumplimiento de la firma.
Específicamente, al observar los resultados que se presentan en el cuadro 8, puede afirmarse al 1% de significación estadística, que no existe la suficiente evidencia para no rechazar la hipótesis de que durante cada uno de los años del periodo estudiado, existió una diferencia significativa entre las probabilidades neutrales de incumplimiento y las probabilidades de incumplimiento de las firmas.

En adelante, se seguirán presentando los resultados de las probabilidades neutrales riesgo de incumplimiento ya que a pesar de que en este trabajo se sigue a Samaniego et al. (2007), cuesta aceptar del todo que el crecimiento de los activos de las empresas es similar al crecimiento del PIB. Se ha explicado cómo la tasa de crecimiento podría incidir en la probabilidad de incumplimiento de una compañía y, por supuesto, la tasa de crecimiento utilizada en este estudio debería refinarse mediante modelos capm, como proponen Löffler y Posch (2007), de tal manera que se pudiese contar con una estimación más precisa del crecimiento de los activos de una compañía. En consecuencia, los resultados de este estudio no acumulan evidencias en la dirección del trabajo de Crosbie y Bohn (2003), en el cual la tasa libre de riesgo o la tasa de crecimiento de los activos de la empresa tienen poco poder discriminante para la estimación de la probabilidad de incumplimiento de una compañía.
3.4 Probabilidades de incumplimiento y tasas de recuperación por sector
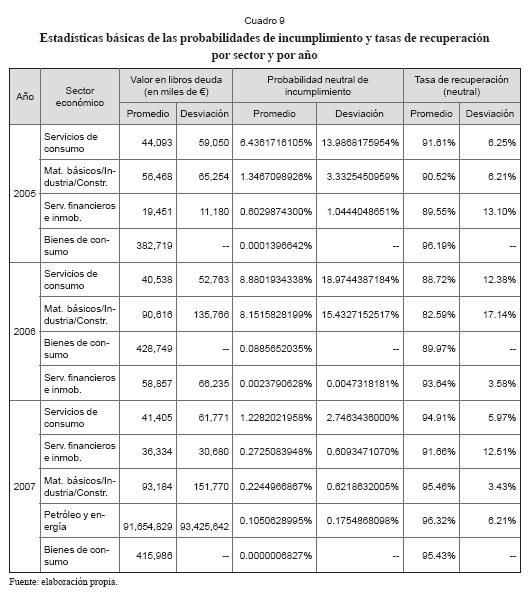
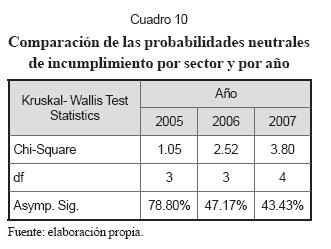
En el cuadro 9 se presentan los resultados de nivel de deuda, probabilidad neutral de incumplimiento y las tasas de recuperación por sector. Dentro de cada año los sectores se han ordenado de manera descendente de acuerdo con la probabilidad neutral de incumplimiento. En el año 2005, las empresas de los sectores de servicios de consumo, materiales básicos/ industria/construcción y las de servicios financieros e inmobiliario presentaron, en su orden, las mayores probabilidades neurales de incumplimiento en promedio. En 2006, las probabilidades más altas de incumplimiento se presentaron en las empresas del sector de servicios de consumo seguidas de las del sector de materiales básicos/industria/ construcción y luego las del sector de bienes de consumo. En 2007, las probabilidades neutrales de incumplimiento más altas se presentaron en su orden, el sector de servicios de consumo, el sector de servicios financieros e inmobiliario y luego el sector de materiales básicos/industria/ construcción. Sin embargo, los resultados del estudio a nivel de sector también indican que, mediante la aplicación del test de Kruskal-Wallis (cuadro 10) y al 1% de significación estadística, no se puede rechazar la hipótesis de que no hubo diferencias estadísticas significativas en los años 2005, 2006 y 2007 entre las probabilidades neutrales de incumplimiento de las empresas agrupadas por sectores según la clasificación del mercado de valores colombiano.
4. Comentarios generales
En la presente investigación se utiliza el modelo de Merton (1974), que limita su aplicación a las empresas de las cuales se dispone de información bursátil; sin embargo, las razones que justifican la utilización de este modelo concreto en nuestra investigación son principalmente las dos siguientes. En primer lugar, el modelo de Merton (1974) nos da estimaciones de las probabilidades de incumplimiento y de la tasas de recuperación de la deuda dado el incumplimiento. Calculadas las probabilidades de incumplimiento y las tasas de recuperación, las empresas pueden darle el tratamiento a su cartera como si fuera una cartera de una empresa del sector de los seguros. Mediante la aplicación de conceptos de la teoría actuarial se puede modelar la pérdida total a que estarían expuestas las compañías por incumplimiento de sus clientes14.
Se menciona la teoría actuarial porque en ella podemos encontrar una metodología para calcular unas provisiones como indicadores de las pérdidas a que estaría expuesta la empresa por incumplimientos de sus clientes. Aplicar la teoría actuarial requiere que tratemos el conjunto de las cuentas por cobrar a clientes de una compañía del sector real o la cartera de créditos dadas a los clientes de una entidad de crédito, como una cartera de seguros en la cual se conoce el número de elementos que la componen, los montos de las exposiciones por cada elemento, las probabilidades de incumplimiento de cada elemento y las tasas de recuperación si se llega a presentar el incumplimiento. Las tres variables mencionadas son objeto de estudio en el modelo de Merton (1974) lo que facilitaría la aplicación de conceptos de la teoría actuarial para la gestión de riesgo de crédito en términos de cuantificar las pérdidas por exposición a dicho riesgo.
Uno de los objetivos de la gestión del riesgo y, en particular, del riesgo de crédito es que las empresas puedan conocer los niveles de exposición al riesgo y que puedan tomar medidas para minimizar las pérdidas por exposición a dicho riesgo. Consideramos que la complementariedad que se puede obtener de aplicar la teoría financiera tradicional y la teoría actuarial, es de gran relevancia para alcanzar dicho objetivo de la gestión de riesgos.
En segundo lugar, las probabilidades y las tasas de recuperación dado el incumplimiento pueden relacionarse con los indicadores contables de las mismas compañías que cotizan en Bolsa. Luego, a través del significado de la Generalización Científica, las empresas que no cotizan en Bolsa o que no disponen de información de clasificación de sus clientes como buenos o malos, pero que sí disponen de su información contable, podrían tener una alternativa para la estimación de dicha probabilidad de incumplimiento. Aunque la relación entre los indicadores contables y la probabilidad de incumplimiento no se aborda en este documento, se reitera la importancia que tiene la aplicación del modelo de Merton (1974) en esta fase de la investigación del proyecto de donde se deriva este artículo.
Conclusiones
En este documento se han cuantificado la probabilidad neutral de incumplimientos y las tasas de recuperación dado el incumplimiento para empresas que cotizaron en la Bolsa de Valores de Colombia en el periodo 2005-2007. El análisis de los resultados nos permite concluir que:
• Durante el periodo de estudio se puede apreciar una relación positiva entre la tasa libre de riesgo y la tasa de crecimiento del PIB.
• En la medida en que se presentó una mayor capitalización bursátil también se incrementó el endeudamiento de las empresas consideras en el estudio.
• Se aprecia una correlación negativa entre el valor de los activos de las firmas y su volatilidad.
• La volatilidad del capital propio estimada con la desviación estándar disminuyó a una tasa del 13,10%, mientras que la estimada a través de la volatilidad histórica lo hizo a una tasa del 13,25% de 2005 a 2007. Sin embargo, al 1% de significación estadística, durante el periodo analizado no se puede rechazar la hipótesis de queno hubo diferenciasignificativaentre la volatilidad del capital propio calculada con la desviación estándar y la volatilidad histórica de los retornos del capital propio.
• No se puede rechazar la hipótesis de que existieron diferencias significativas entre las probabilidades neutrales de incumplimiento y las probabilidades de incumplimiento de las compañías.
• A nivel de sectores, al 1% de significación estadística, no se puede rechazar la hipótesis de que no hubo diferencias significativas en las probabilidades de incumplimiento. Para los años analizados se observó que las empresas del sector de servicios de consumo presentan mayor probabilidad de incumplimiento de la deuda financiera, seguidas de las empresas del sector materiales básicos/ industria/construcción. Las empresas del sector de petróleo y energía y la de bienes de consumo presentaron la probabilidad más baja de incumplimiento de la deuda financiera.
Por todo lo anterior, las empresas del sector financiero que otorgaron deuda a las compañías que se transaron en la Bolsa de Valores de Colombia y que presentaron alta bursatilidad experimentaron una disminución en la probabilidad incumplimiento del año 2005 a 2007.
Para un desarrollo posterior se plantea calcular la tasa de crecimiento de los activos de las compañías mediante el capM, con el fin de obtener unas probabilidades de incumplimientos más ajustadas a la realidad de cada empresa. Si se dispone de información más detalla de cada compañía sobre sus estructuras de vencimiento de la deuda, se podría aplicar el modelo de Geske (1977), a través del cual se pueden obtener estimaciones de las probabilidades de incumplimiento de las compañías tanto de la deuda de corto plazo como de la deuda de largo plazo.
Los resultados obtenidos en este trabajo son de gran importancia, no únicamente por sí mismos, sino también porque pueden ser utilizados para la cuantificación del valor en riesgo (VaR) y el Tail VaR (TVaR) por exposición a riesgo de crédito de las empresas mediante la aplicación de conceptos de la teoría actuarial. Específicamente, una futura investigación puede tomar en consideración los resultados de este estudio y estimar el VaR y el TVaR mediante el enfoque de distribución de la pérdida total (lda) a través de los modelos individual y colectivo de riesgo, el enfoque de Basilea ii y por simulación utilizando distintas distribuciones estadísticas.
Notas al pie de página
1 Jarrow y Protter (2004).
2 Crouhy et al. (2000).
3 Ramaswamy (2005) y Dunkel y Weber (2007).
4 Atiya (2001).
5 Wei (2008) y Zhu y Chiu (2007).
6 Entrevistas efectuadas en septiembre de 2007 a directores de riesgo de entidades financieras colombianas.
7 Geske (1977) considera que el valor de los activos del capital propio sigue el comportamiento de una opción call compuesta con subyacente el valor de los activos de la firma. De esta manera estima la probabilidad de incumplimiento de corto plazo y la probabilidad de incumplimiento a largo plazo dado que no se ha incumplido la deuda de corto plazo.
8 Samaniego et al. (2007) utilizan la tasa de crecimiento del PIB de España en el 2003 como una proxy de la tasa de crecimiento de los activos (µ) de las empresas españolas que se transan en el mercado de valores español. Löffler y Posch (2007) proponen estimar µ, para cada firma a través del CAPM.
9 Deng (2005), Jackson et al. (1999) y Crouhy et al. (2000).
10 JP Morgan and Company (1997).
11 Siguiendo el algoritmo sugerido por Löffler y Posch (2007), en Excel mediante el procedimiento solver se realizaron algunas estimaciones de lavolatilidad y del valor de los activos de las empresas encontrando, que en muchas ocasiones el valor de la empresa se estimaba como la suma del valor nominal de la deuda y el valor del capital propio; el mismo valor inicial que es sugerido por Löffler y Posch (2007). Por esta situación se tomó como estimaciones para la volatilidad y el valor de los activos de la empresa las obtenidas mediante Mathematica 6.0.
12 La ventana de análisis, 2005-2007, quedó determinada por la homogenización del periodo de estudio de la investigación del cual hace parte este artículo. En el proyecto de investigación más general se incluyen empresas colombianas y empresas españolas, las cuales son objeto de comparación razón por la cual la unidad monetaria que se ha utilizado en este trabajo es el Euro.
13 En este estudio se emplean los test no paramétricos del rango de signos de Wilcoxon y el test de Kruskal y Wallis para muestras relacionadas y para muestras independientes ya que no asumen ningún supuesto a priori sobre la distribución de donde provienen los datos. Sin embargo, hay que tener en cuenta que el test de rangos de Wilcoxon para dos muestras relacionadas no considera los empates entre las variables validadas; razón por la cual cuando los empates de las variables validadas superaban el 50% de los datos, se optó por no rechazar la hipótesis de igualdad entre los valores de las variables validadas.
14 Chen y Panjer (2009) y Carreras (2006).
Lista de referencias
1. Altman, E. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. Journal of Finance, 23, 589-609. [ Links ]
2. Altman, E. (2000). Predicting financial distress of companies: Revisiting the Z-Score and Zeta Models. Recuperado el 29 de septiembre de 2008, de http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.25.1884. [ Links ]
3. Altman, E.; Haldeman, R. and Narayanan P. (1977). Zeta analysis. A new model to identify bankruptcy risk of corporations. Journal of Banking and Finance, 1, 589-609. [ Links ]
4. Altman, E.; Marco, M. and Varetto, F. (1994). Corporate distress diagnostics: Comparison using linear discriminant analysis and neural networks (the Italian experience). Journal of Banking and Finance, 18, 505-529. [ Links ]
5. Altman, E. and Sabato, G. (2005). Modeling credit risk for SMEs: Evidence from the US market. Recuperado el 29 de septiembre de 2008, de http://ssrn.com/abstract=872336. [ Links ]
6. Arora, N.; Jeffrey R. and Fanlin, Z. (2005). Reduced form vs. structural models of credit risk: A case study of three models. Journal of Investment Management, 3 (4), 43-67. [ Links ]
7. Atiya, A. F. (2001). Bankruptcy prediction for credit risk using neural networks: A survey and new results. IEEE Transactions on Neural Networks, 12, 929-935. [ Links ]
8. Basilea (1988). Convenio de capital. Comité de Supervisión Bancaria de Basilea, Convenio de Capital. Banco de Pagos Internacionales. Basilea, Suiza. [ Links ]
9. Basilea (2001). Convenio de capital. Proceedings of the 11th. International Conference of Banking Supervisors, 20-22 september, Basilea, Suiza. [ Links ]
10. Basilea (2004). Convergencia internacional de medidas y normas de capital. Comité de Supervisión Bancaria de Basilea, Marco revisado junio. Banco de Pagos Internacionales. Basilea, Suiza. [ Links ]
11. Black, F. and Scholes, M. (1973). The pricing of options and corporate liabilities. Journal Political Economy, 81 (3), 637-654. [ Links ]
12. Carreras, P. M. (2006). Credit risk modeling using insurance methods. Barcelona: Tesis doctoral Universidad de Barcelona. [ Links ]
13. Chen, C. J. and Panjer, H. (2003). Unifying discrete structural models and reduced-form models in credit risk using a jump-diffusion process. Insurance: Mathematics and Economics, 33 (2), 357-380. [ Links ]
14. Chen, C. J. and Panjer, H. (2009). A Bridge from Ruin Theory to Credit Risk. Review of Quantitative Finance and Accounting, 32 (4), 373-403. [ Links ]
15. Chen, Z. F.; Liv, Y. Y. and Wang, X. F. (2008). Comparative study on credit risk models. Proceedings of 2008 International Conference on Risk and Reliability Management, I-II, 189-191. [ Links ]
16. Coyle, B. (2000). Corporate credit analysis. Chicago: Amacom. [ Links ]
17. Crosbie, P. and Bohn, J. R. (2003). Modeling Default Risk. KMV Corporation. [ Links ]
18. Crouhy, M.; Galai, D. and Mark, R. (2000). A comparative analysis of current credit risk models. Journal of Banking and Finance, 24, 59-117. [ Links ]
19. DeLara, H.A. (2003). Medición y control de riesgos financieros. México: Limusa Noriega Editores. [ Links ]
20. Deng, Z. W. (2005). Moody's KMV model and its apply in credit risk evaluation of corporate. Proceedings of International Conference on Construction and Real Estate Management, 1-2, 773-775. [ Links ]
21. Duan, J. C. and Andras, F. (2009). Estimating the structural credit risk model when equity prices are contaminated by trading noises. Journal of Econometrics, 150 (2), 288-296. [ Links ]
22. Dunkel, J. and Weber, S. (2007). Efficient Monte Carlo methods for convex risk measures in portfolio credit risk models. Proceedings of the 2007 Winter Simulation Conference, 1-5, 937-945. [ Links ]
23. Elizalde, A. (2005). Credit Risk Models II: Structural Models. Madrid: CEMFI and UPNA. [ Links ]
24. Ericsson, J. and Reneby, J. (2005). Estimating structural bond pricing models. Journal of Business, 78 (2), 707-735. [ Links ]
25. Geske, R. (1977). The valuation of corporate liabilities as compound options. Journal of Financial and Quantitative Analysis, 12 (4), 541-552. [ Links ]
26. Greene, W. H. (2000). Econometric Analysis, 2nd . ed., New York: Prentice Hall Internacional Editions. [ Links ]
27. International Actuarial Association (2004). A global Framework for Insurer Solvency Assessment. Research Report of the Insurer Solvency Assessment Working Party. [ Links ]
28. Jackson, P.; Nickell, P. and Perraudin, W. (1999). Credit risk modeling. Financial Stability Review, 94-121. [ Links ]
29. Jarrow, R. A.; Protter, P. and Sezer, A. D. (2007). Information reduction via level crossings in a credit risk model. Finance and Stochastics, 11, 195-212. [ Links ]
30. Jarrow, R.A. and Protter, P.(2004). Structural versus reduced form models: A new information based perspective. Journal of Investment Management, 2 (2), 1-10. [ Links ]
31. Jones, P.; Mason, P. S. and Rosenfeld, E. (1984). Contingent claims analysis of corporate capital structures: An empirical investigation. Journal of Finance, 39 (3), 611-625. [ Links ]
32. JP Morgan and Company (1997). CreditMetrics. Documento Técnico. Nueva York: JP Morgan. [ Links ]
33. Loffler, G. and Posch, P. (2007). Credit Risk Modeling. England: John Wiley and Sons. [ Links ]
34. Márquez, J. (2006). Una nueva visión del riesgo de crédito. México: Limusa - Noriega Editores. [ Links ]
35. Merton, R. (1974). On the pricing of the corporate debt: the risk structure of interest rates. Journal of Finance, 29 (2), 449-470. [ Links ]
36. Pederson, G. D. and Zech, L. (2009). Assessing credit risk in an agricultural loan portfolio. Canadian Journal of Agricultural Economics, 57, 169-185. [ Links ]
37. Ramaswamy, S. (2005). Simulated credit loss distribution. Journal of Portfolio Management, 31, 91-99. [ Links ]
38. Saavedra, G. M. L. and Saavedra, G. M. J. (2010). Modelos para medir riesgo de crédito de la banca. Cuadernos de Administración, 23 (40), 295-319. [ Links ]
39. Samaniego, R.; Trujillo, A. y Martin, J. L. (2007). Un análisis de los modelos contables y de mercado en la evaluación del riesgo de crédito: aplicación al mercado bursátil español. Revista europea de dirección y economía de la empresa, 16 (2), 93-110. [ Links ]
40. Seidler, J. and Petr, J. (2009). Implied market loss given defaultin the Czech Republic: Structural-model approach. Finance a Uver/Czech Journal of Economics and Finance, 59 (1), 20-40. [ Links ]
41. Soros, G.; Simons, J.; Paulson, J.; Griffin, K. and Falcone, P. (2008). Statement before the U.S House of Representatives Committee on oversight and Government Reform. U.S. Congress. Recuperado el 16 de noviembre de 2008, de http://republicans.oversight.house.gov. [ Links ]
42. Vassalou, M. and Xong, Y. (2004). Default risk in equity returns. Journal of Finance, LIX (2), 831-868. [ Links ]
43. Wei, R. (2008). Development of credit risk model based on fuzzy theory and its application for credit risk management of commercial banks in China. 4th. International conference on wireless communications, networking and mobile computing, 1-31, 10339-10342. [ Links ]
44. Zech, L. and Pederson, G. (2004). Application of credit risk models to agricultural lending. Agricultural Finance Review, 64, 91-106. [ Links ]
45. Zhu, Y. and Chiu, W. H. (2007). Credit risk assessment using the RBF neural network. Information. Management and Algorithms, II, 125-128. [ Links ]