Introducción
La enseñanza de las ciencias tiene un gran desafío: cómo generar en el aula situaciones de enseñanza en la que los estudiantes se pregunten sobre los fenómenos naturales y elaboren explicaciones utilizando los modelos. De allí, la importancia de la argumentación como una competencia indispensable para promover el pensamiento crítico en los procesos de enseñanza y aprendizaje de los conceptos científicos, con el fin de lograr una comprensión profunda de la realidad.
Enseñar y aprender ciencias requiere de estrategias basadas en el lenguaje, es decir, el aprendizaje es un proceso social en el cual las actividades discursivas son esenciales. Se reconoce aquí una estrecha relación entre las competencias comunicativas y el aprendizaje de los modelos científicos y se arriesga la hipótesis de que a una mejora en dichas competencias corresponde un aprendizaje de mayor calidad, y que aprender a pensar es aprender a argumentar (Henao et ál., 2008).
En relación con lo anterior, se establece la importancia de aprender a argumentar, al tiempo que se reconoce la necesidad de indagar, en primer lugar, cómo los estudiantes elaboran sus argumentos: ¿Qué cuenta para ellos como un dato?, y ¿qué como conclusión o explicación?, ¿qué tipo de justificaciones utilizan y en qué casos las utilizan?, ¿en cuáles situaciones utilizan modelos, conceptos, leyes o principios disciplinares para justificar sus conclusiones?, ¿qué procesos siguen para argumentar mientras resuelven problemas? Y ¿qué niveles epistémicos es posible identificar en sus argumentos escritos? Son, entre otras, preguntas clave como punto de partida para enseñar a razonar y a argumentar (Henao et ál., 2008).
En definitiva, asumimos que promover las prácticas argumentativas en el aula de clase, conlleva reconocer que la argumentación es una actividad social. Dicha actividad permite, en el estudiante la cualificación en los usos de lenguajes, el desarrollo de habilidades cognitivas, sociales y emocionales, la comprensión de los conceptos y teorías estudiadas y la formación como un ser humano crítico, capaz de tomar decisiones como ciudadano (Ruiz, 2015).
Lo anterior originó la pregunta central de este trabajo: ¿Cuáles son los niveles argumentativos y su relación con los modelos explicativos del concepto de circuitos eléctricos en los estudiantes de grado once de la Institución Educativa Pablo Emilio Riveros del municipio de Acacias-Meta?
Antecedentes
Numerosas investigaciones se identificaron y se han planteado sobre el concepto de circuito eléctrico, entre ellas tenemos: "Los cómics en la enseñanza de la Física: Diseño e implementación de una secuencia didáctica para circuitos eléctricos en bachillerato" (Agüero et ál. 2012); "Aprender competencias en una propuesta para la enseñanza de los circuitos eléctricos en Educación Primaria" (Pro Bueno et ál. 2010); "Las interpretaciones de los estudiantes de BUP sobre electrocinética ejemplos con circuitos de corriente continua" (Acevedo, 1989); y, por último, la propuesta circuitos eléctricos: "Una aplicación de un modelo de enseñanza-aprendizaje basado en las ideas previas de los alumnos" (Varela et ál., 1988).
Los estudios anteriormente relacionados brindaron elementos de orden teórico y metodológico que orientaron el desarrollo del presente estudio, ya que en algunos de estos el trabajo fue realizado con estudiantes en diferentes niveles educativos y se plantearon diversos campos de conocimiento en los que se desarrollaron procesos de argumentación y se mostraron avances en los grupos de cada una de las investigaciones; sin embargo, la presente investigación hace la diferencia, pues además de identificar niveles iniciales y finales, la intencionalidad investigativa también fue la comprensión de los diferentes modelos explicativos sobre el concepto de circuitos eléctricos, trascendiendo el concepto de corriente eléctrica y el modelo de circuito eléctrico sencillo (modelo de Volta).
Marco teórico
La importancia de la argumentación en el aprendizaje de las ciencias
La argumentación es una forma de discurso que debe ser apropiada por los estudiantes y enseñada explícitamente en la clase de ciencias; así, la alfabetización científica se consigue a partir de la lectura crítica de diferentes fuentes, la participación en debates y la argumentación. En esa medida, es necesario argumentar en la clase de ciencias porque el discurso ayuda a construir conocimiento científico, promueve la interacción social, desarrolla procesos de pensamiento a través del lenguaje y juega un papel importante en la construcción de explicaciones, modelos y teorías. Una de las principales razones para enseñar argumentación en la clase de ciencias, sostiene Sánchez et ál. (2013), es que los estudiantes deben tener una idea clara de lo que significa la ciencia, especialmente la naturaleza social del conocimiento científico, y para ello se hace necesario que los jóvenes construyan y analicen argumentos científicos con implicación social en el aula. Ello implica, además, motivar en los estudiantes la reflexión sobre sus propios procesos de aprendizaje y sobre la forma en que se estructuran sus conocimientos. El compromiso epistemológico frente a los estudiantes, debe prevalecer más que la crítica sobre las observaciones inconsistentes o irrelevantes de los demás, debe tener en cuenta el poder explicativo que se traduce en cambios conceptuales. (Sánchez et ál., 2013).
El modelo de Toulmin es explicado con claridad por (Sardá, 2000) al afirmar que: según este modelo, en una argumentación, a partir de unos datos obtenidos o de unos fenómenos observados, justificados de forma relevante en función de razones fundamentadas en el conocimiento científico aceptado, se puede establecer una afirmación o conclusión. Esta afirmación puede tener el apoyo de los calificadores modales y de los refutadores o excepciones (Sardá, 2000).
De esta forma, los autores ilustran claramente la función que cumple cada órgano del argumento en el modelo argumentativo de Toulmin. Este modelo, ha sido objeto de estudio en diferentes áreas. Entre los estudios que se han realizado para explicarlo, vale la pena citar el adelantado por (Osborne, 2004), quienes, estudiando ambientes de aprendizaje que favorecieran la enseñanza de la argumentación en ciencias, proponen una escala que permite la calificación de la calidad de la argumentación. Dicha escala consta de cinco niveles que incluyen los elementos definidos en el modelo argumentativo de Toulmin. La Tabla 1 ilustra dicha escala.
Tabla 1 Niveles de Argumentación propuestos por Erduran, Simon y Osborne, 2004
| Nivel | Descripción |
| 1 | La argumentación consiste en argumentos que son solo una simple afirmación, dato o conclusión |
| 2 | La argumentación tiene argumentos que constan de afirmaciones o datos y justificaciones, pero sin refutaciones |
| 3 | La argumentación tiene argumentos con una serie de afirmaciones, datos o respaldos y justificaciones con refutación débil ocasional |
| 4 | La argumentación tiene argumentos con una serie de afirmaciones o datos, justificaciones o respaldos y garantías con refutación débil ocasional |
| 5 | Argumentación que manifiesta un amplio argumento con más de una refutación. |
Fuente: (Pinochet, 2015, p. 320). Traducida y adaptada de Osborne et ál. (2004).
Los niveles argumentativos surgen de la necesidad de ahondar las explicaciones que dan los estudiantes sobre los conceptos científicos en la medida que se van apropiando del lenguaje adecuado que facilite describir, relacionar e interpretar situaciones propias de su contexto cuando, en los escenarios educativos, el debate se reduce a cierto número de estudiantes y al no intercambio de ideas, sino a la búsqueda de una respuesta correcta, los argumentos serán simples. Es difícil llegar a argumentos de una alta calidad, pues en la mayoría de casos los contraargumentos provienen de los otros, pero estas discusiones requieren que el otro o los otros estén en el mismo nivel de conversación, no que alguien sepa más que otro, o que participe más. Si no se logra llegar a lo anteriormente mencionado, será complicado que los estudiantes lleguen a partir de una pregunta a generar una serie de tesis que puedan o no estar soportadas por garantías, las cuales también pueden estar soportadas por datos que pueden ser estadísticos, hechos, ejemplos, etc., y sería una limitación para que los estudiantes lleguen al nivel argumentativo 5 de Osborne, Erduran y Simón.
Modelos en la enseñanza de las ciencias
Si consideramos que las ideas iniciales de los estudiantes son distintas y que sus procesos de razonamientos son personales y diferentes para cada uno de ellos, no se puede esperar que todos ellos desarrollen el mismo modelo y de la misma forma. Por ello, la enseñanza en ciencias se debe fundamentar en modelos como en el proceso de construcción de modelos, por lo que el aprendizaje es un proceso gradual, y la construcción de modelos constituye los cimientos de este.
En esta misma línea de investigación en la enseñanza de las ciencias, que propende por una formación desde la argumentación y que tiene como fundamentos explorar, desarrollar y modificar las ideas o los conocimientos previos de los estudiantes, se encuentra la propuesta teórica sobre la elaboración de modelos, desarrollada por (Greca, 1998), Johnson-Laird (1983 en Justi, 2006), entre otros autores, y antes de describir sus aspectos centrales, se explican algunos conceptos que articulan dicha propuesta: modelos, modelos mentales y modelos conceptuales; para comprender su articulación desde la enseñanza.
Implicaciones de la teoría de modelos en la enseñanza de las ciencias
De acuerdo con lo expresado, los modelos mentales elaborados por los estudiantes son incompletos y van siendo ampliados o modificados a medida que se generan espacios para tal propósito, considerando que este proceso no es el producto de la transmisión de significados, sino una consecuencia de la evolución cognitiva que resulta de la interacción entre los modelos mentales del estudiante y los modelos conceptuales según afirman Oliva y Aragón (2009).
Justi (2006), propone los siguientes argumentos que justifican el papel que los modelos deben desempeñar en la enseñanza de las ciencias:
Aprender ciencias. Los estudiantes deben tener conocimientos sobre la naturaleza, ámbito de aplicación y limitaciones de los principales modelos científicos (ya sean estos consensuados, es decir, aceptados actualmente por la comunidad científica, o bien aquellos que hayan sido aceptados en un determinado contexto).
Aprender sobre ciencias. Los estudiantes deben comprender adecuadamente la naturaleza de los modelos y ser capaces de evaluar el papel de los mismos en el desarrollo y difusión de los resultados de la indagación científica.
Aprender a hacer ciencias. Los estudiantes deben ser capaces de crear, expresar, comprobar y justificar sus propios modelos.
Lo anterior significa, según Justi y Gilbert "que la construcción de modelos es una actividad con mucho potencial para implicar a los estudiantes en hacer ciencias, pensar sobre las ciencias y desarrollar pensamiento científico y crítico" (2003, p.178). De esta forma, las ciencias dejarían de ser algo que se lee en los libros, para transformarse en una actividad mediante la cual los fenómenos se estudian de forma activa, en una atmósfera de cooperación participativa, con más tiempo y recursos compatibles.
En la tabla 2 encontramos las principales ideas de los diferentes modelos explicativos de la pila en un circuito sencillo de corriente continua.
Tabla 2 Diferentes modelos explicativos de la pila en un circuito sencillo de corriente continua
| Hechos experimentales en relación con la función de la pila en un circuito | Modelo de Volta | Modelo colombiano | Modelo de Ohm | Modelo de Kirchhoff |
| - Pila de Volta I Al poner en contacto dos metales diferentes a través de un “conductor húmedo” se encuentra que cada uno de ellos adquiere una carga neta y opuesta en signo | La ‘fuerza electromotriz’ de la pila es la capacidad para separar cargas y mantenerlas separadas | La fuerza electromotriz de la pila no es otra cosa que la capacidad que tienen algunos cuerpos de generar electricidad en otros | Noción de ‘fuerza electroscópica’, relacionada con la densidad superficial de carga | La fuerza electromotriz que separa las cargas en la pila mide la energía que se da a la unidad de carga que circula por el circuito. La pila genera diferencia de ‘fuerza electroscópica’ que es identificada como la magnitud diferencia de potencial definido por Poisson |
| Electricidad y cuerpos I Cargados | Magnitud cualitativa. Fluido eléctrico | Magnitud cuantitativa. Fluido eléctrico | Magnitud cuantitativa. Fluido eléctrico | Magnitud cuantitativa La noción de fluido eléctrico empieza a cuestionarse |
| - Corriente eléctrica I en un circuito | No se sabe medir | No se sabe medir | La corriente se debe a diferencia entre dos puntos de valores de‘ fuerza electroscópica’ | Magnitud cuantitativa, puede medirse con el galvanómetro |
| Circuitos eléctricos I rudimentarios de corriente continua | Noción de circuito cerrado | Cuerpos cargados con electricidad de distinto signo se atraen a través de un conductor que los une | Analogía con la teoría del calor de Fourier. La corriente eléctrica circula por el circuito debido a la diferencia entre los valores de ‘fuerza electroscópica’ (densidad superficial de carga) entre dos puntos del mismo | La corriente circula debido a la diferencia de potencial entre dos puntos del circuito. Considera el movimiento de corriente como un balance entre la energía generada por la pila y la consumida en el circuito |
Fuente: Guisasola et ál., 2008, p. 1604.
Metodología
La presente investigación se desarrolló bajo un enfoque cualitativo de alcance descriptivo en tres momentos: el primero fue de Ubicación o diagnóstico, se identificaron los modelos explicativos iniciales de los estudiantes que hicieron parte de este estudio mediante un cuestionario inicial de lápiz y papel; el segundo, desubicación o intervención, se aplicó una unidad didáctica diseñada para intervenir los niveles argumentativos y los modelos explicativos del concepto de circuitos eléctricos de los estudiantes y el tercer momento de reenfoque o cierre, en torno al análisis de los cambios en los modelos explicativos y de los niveles argumentativos que utilizaron para explicar el concepto sobre circuitos eléctricos después de la aplicación de la unidad didáctica mediante un debate grupal.
En la investigación participaron 24 estudiantes de grado 11 entre los 16 y 17 años del Colegio Pablo Emilio Riveros de la modalidad de Electrónica, que es elegida por los estudiantes para cursarlos durante dos años de la media técnica.
Se aplicó un instrumento inicial y final para identificar los niveles argumentativos y los modelos explicativos del concepto de circuitos eléctricos comprendiendo la transición entre un nivel y otro, de igual manera en los modelos explicativos en el tránsito de un modelo a otro; se construyó un instrumento escrito con once preguntas, desarrolladas antes y después de la intervención didáctica.
Unidad didáctica
En el momento de desubicación o intervención, partiendo de los resultados iniciales obtenidos se diseñó y se aplicó una unidad didáctica con la que se abordaron los modelos explicativos que los estudiantes de grado 11 utilizan para explicar el concepto de circuitos eléctricos, al igual que su manera de argumentar. Mediante esto, se buscó la construcción compartida de conceptos a través de la problematización y la promoción de interacción lingüística, guiada por el docente.
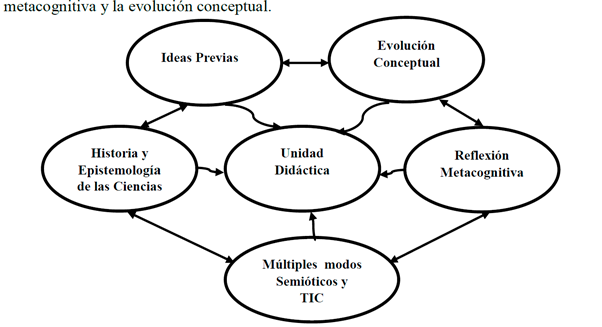
Según Tamayo (2006) y Sánchez et ál. (1993), la unidad didáctica es un proceso flexible de planificación de la enseñanza de los contenidos relacionados con un campo del saber específico para construir procesos de aprendizaje en una comunidad determinada. Debe estar constituida a partir de las ideas previas, la historia y la epistemología de las ciencias, los distintos modos de representación semiótica y las Tic, la reflexión metacognitiva y la evolución conceptual.
La UD estuvo enmarcada en doce sesiones de clase, teniendo como base el instrumento de ideas previas (cuestionario inicial), los obstáculos y modelos explicativos encontrados a partir de este, centrada en la argumentación y asociada al concepto de circuito eléctrico, bajo el modelo de argumentación de Toulmin a partir de los constructos teóricos de Tamayo. Esta intervención fue realizada en tres momentos: ubicación, desubicación y reenfoque.
En el momento de reenfoque o cierre el docente abordó el concepto de argumentación partiendo del modelo argumentativo de Os-borne et ál. (2004) y lo ilustró con un ejemplo de la cotidianidad. Con esto, los invitó a resolver, en pequeños grupos, una actividad en la que se les propone desarrollar una discusión y llegar a acuerdos para luego responder por escrito. Las respuestas así obtenidas, fueron puestas en la plenaria del grupo y sometidas al consenso general. Cada grupo defendió su posición y se desarrollaron discusiones que permitieron enriquecer los aportes de cada grupo, favoreciendo el aprendizaje de los conceptos y promoviendo la competencia argumentativa.
Para determinar los modelos explicativos se hizo uso de la información contenida en la tabla 2 (Características de los modelos explicativos), en la que se recogen los principales elementos con los que la literatura describe cada uno de los modelos explicativos. Mientras que, para definir los niveles de argumentación se utilizó la tabla 1 (Niveles de argumentación), estas herramientas permitieron dar orden a los datos obtenidos.
Posteriormente, se realizó una revisión y transcripción de los materiales de audio que se obtuvieron durante el desarrollo de este trabajo, para la transcripción del material, se utilizó la metodología propuesta por Candela (2001), con la que se facilita este proceso. De acuerdo con Hernández et ál. (2010), las transcripciones son leídas y releídas, tanto como sea necesario, para poder comprender el sentido general de los datos. Hecho esto, los datos son organizados de acuerdo con el tipo de datos o teniendo en cuenta el instrumento que permitió la recogida de los datos. Finalmente, y ya con los datos organizados y separados, se realiza una triangulación de datos (Hernández et ál., 2010). Lo cual, permite dar mayor validez a las categorías identificadas.
Para el desarrollo del análisis comprensivo se seleccionaron 6 estudiantes del grupo inicial constituido por 24 estudiantes; el criterio fue el resultado del cuestionario inicial sobre modelos explicativos y niveles argumentativos iniciales, teniendo en cuenta que en los estudiantes se caracterizaron varios modelos explicativos en las situaciones propuestas; respecto a los niveles argumentativos se identificaron los niveles 1, 2 y 3. También se tuvo como referente la participación en todas las actividades, ya que los estudiantes no estuvieron presentes en algunas clases durante el desarrollo de la unidad didáctica.
Resultados
Las respuestas proporcionadas por los estudiantes fueron analizadas teniendo en cuenta las convenciones citadas en la Tabla 3, con el fin de identificar la estructura del argumento y la recurrencia de los marcadores discursivos, que son expresiones como: esto es, así las cosas, sin embargo, por cierto, pues, por ende, es decir, por ejemplo, además y otras unidades lingüísticas especializadas en encadenar los diferentes fragmentos discursivos señalando explícitamente el tipo de relación semántica que existe entre ellos, guiando así la interpretación del discurso que se transmite, usados en sus respuestas; los cuales aparecen resaltados en negrita.
Tabla 3 Convenciones utilizadas para el análisis de los argumentos
| Símbolo | Nombre | Característica |
| T | Tesis o hipótesis | Tesis o hipótesis. Permite defender un punto de vista o un asunto |
| D | Datos | Datos, son evidencias que apoyan la tesis o hipótesis (citas, reportes) |
| J | Justificaciones | Justificaciones, con esta encuentra una relación entre la tesis y los datos |
| R | Refutación | Refuta el argumento |
| E | Estudiante | Unidad de trabajo |
| P | Pregunta | Están en el instrumento |
Fuente: elaboración propia.
Terminada la unidad didáctica, se realizó la actividad de modelos finales, con el fin de identificar el progreso de los modelos explicativos y los niveles argumentativos de los educandos.
En síntesis, los estudiantes presentaron cambios en sus modelos explicativos sobre el concepto de circuito eléctrico, pues ellos lograron describir, reconocer y justificar las principales ideas de los diferentes modelos explicativos, partiendo desde el concepto de circuito elemental hasta llegar al circuito más complejo. Además, al finalizar en todas sus respuestas hace uso de modelos explicativos, de tal manera que el desarrollo de la unidad didáctica permitió el enriquecimiento conceptual de los estudiantes (Arzola et ál., 2011).
Esto nos lleva a pensar, que las actividades diseñadas que se utilizaron durante la aplicación de la unidad didáctica pudieron haber aportado gradualmente en la apropiación de conocimientos específicos sobre el concepto de circuitos eléctricos y sus diferentes modelos explicativos, tal y como afirma Greca (1998), la capacidad de comprender una teoría estará determinada por la capacidad del estudiante para formar modelos, que incluyan las relaciones fundamentales de la teoría y de los cuales sea posible extraer explicaciones y predicciones, que estén de acuerdo con las concepciones científicamente compartidas.
Para terminar, la enseñanza encaminada a partir de la construcción de modelos debe facilitar, que los estudiantes identifiquen los alcances y limitaciones de sus modelos construidos, desarrollen formas de pensar, expresar y explicar los fenómenos físicos, y participen en discusiones que permitan una proximidad a su naturaleza e historia.
Después de aplicar el instrumento final con el propósito de analizar los avances en los niveles argumentativos, ya que los estudiantes presentaban una tendencia hacia el nivel 1, se puede concluir que los estudiantes logran hacer argumentos de mejor calidad si se comparan con los obtenidos en el instrumento inicial. Esta aseveración se hace porque los argumentos escritos presentan una estructura más clara, hay mayor coherencia en sus respuestas, hay uso de una mejor terminología científica.
Es necesario recalcar que una peculiaridad que presentaban los argumentos obtenidos en el instrumento inicial es que carecían de encabezado, es decir, los estudiantes eran muy puntuales a la hora de contestar diferente a las nuevas concepciones, estas presentan una estructura más organizada. Otra característica que se evidenció en el instrumento final es que los estudiantes intentaron hacer justificaciones para sus tesis, apoyada de citas de lo que escuchó de su docente y de las diversas fuentes de información suministradas durante las sesiones desarrolladas, además se observa que utilizan correctamente los signos de puntuación para dar más coherencia al texto.
Es válido aclarar que este tipo de argumentos obtenidos en el instrumento final no presentan aún refutaciones o contraargumentos, tal como se observa en la tabla 4, donde la mayor tendencia es hacia el nivel argumentativo 2 de Erduran et ál. (2004), razón por la cual se debe seguir trabajando con ejercicios que ayuden a aumentar el discurso del estudiante.
Tabla 4 Modelos explicativos y niveles argumentativos presentados en los estudiantes antes y después
| Estudiante | Pregunta | Modelo explicativo inicial Nivel argumentativo inicial | Modelo explicativo final Nivel argumentativo final |
| E1 | P3 | “En la figura No. 2 ya que según la ley de ohm se establece que el voltaje es directamente proporcional a la intensidad de corriente (D), es decir, a mayor voltaje mayor intensidad de corriente (J)” Nivel 1 | “El bombillo que tendrá mayor luminosidad es el de la figura 2 (T), porque tiene dos generadores (pilas) conectados en serie (D), es decir, hay mayor voltaje, por lo tanto, se mueve más corriente, hay mayor fuerza de las pilas para separar las cargas y mantenerlas separadas, en otras palabras, el voltaje es directamente proporcional a la corriente (J)” Nivel 2 |
| E3 | P3 | “La figura 2 porque está recibiendo más voltaje, o energía (D) por parte de las dos pilas, por lo cual iluminaría más” Nivel 1 | “La figura No. 2, porque el voltaje mueve la corriente (T), es decir, a mayor voltaje mayor intensidad de corriente eléctrica, mayor flujo de electrones (D), pues se encuentran conectadas las dos pilas en serie, provocando mayor luminosidad en el bombillo (J)” Nivel 2 |
| E4 | P6 | “Al pagarse o desconectarse un bombillo los demás dejaran de funcionar ya que no sigue transcurriendo la energía (D), se corta el paso” Nivel 1 | “Si se funde o quita un bombillo de los circuitos en serie, el circuito queda abierto (T), es decir, no habrá paso de corriente (D), por ende, los demás bombillos no encenderán puesto que la corriente solo tiene un único camino (J)” Nivel 2 |
| E5 | P7 | “Si en la figura No. 3 y No. 4 se desconecta o se quema uno de los bombillos no sucedería nada (D), la corriente se transmitiría para los demás sin perder la interconexión” Nivel 1 | “Al quitarse o quemarse un bombillo, los demás bombillos funcionarán igualmente puesto que están en paralelo (T), por lo tanto, dicha interrupción no interrumpe el flujo de electrones en las otras ramas del circuito (D), pues cada dispositivo funciona en forma independiente de los demás (J)” Nivel 2 |
| E6 | P9 | “D porque el bombillo estará recibiendo toda la energía de los demás bombillos (D) al ser un solo recorrido para llegar al bombillo D” Nivel 1 | “El bombillo D va a tener mayor luminosidad porque a este llegan todas las cargas de los otros tres bombillos (T), pues en cualquier nudo, la suma de todas las corrientes que entran debe ser igual a la suma de todas las que salen (D), pues la corriente total es la que pasa por el bombillo D y esta se distribuye en el nudo por los bombillos A, B y C (J)” Nivel 2 |
| E10 | P8 | “En la figura 3 las bombillas brillaran con mayor intensidad ya que estos son independientes, dando así más luminosidad (D), ya que es un circuito en paralelo” Nivel 1 | “En la figura 3 brillará más (T), ya que su resistencia que se opone al paso de la corriente es menor (D) y la diferencia de potencial es igual debido a que el circuito está en paralelo (J), en la figura 1 hay mayor resistencia porque en un circuito en serie la resistencia es mayor produciendo menor corriente, por tanto, menor luminosidad en los bombillos (R)” Nivel 3 |
Fuente: elaboración propia.
Conclusiones
Con base en el análisis realizado en los modelos explicativos y los niveles argumentativos de los estudiantes sobre los circuitos eléctricos, y teniendo en cuenta la caracterización de estos y sus cambios en los tres momentos de la investigación, se establecen las siguientes conclusiones:
Se lograron identificar las dificultades mediante la actividad de los modelos explicativos iniciales y elaborar una unidad didáctica para superar obstáculos de aprendizaje en el proceso de enseñanza sobre el concepto de los circuitos eléctricos. Asimismo, se observó en los estudiantes el enriquecimiento de sus modelos explicativos, haciendo uso de los diferentes modelos en el transcurso de la investigación, dependiendo de la situación planteada a resolver para dar respuesta a las situaciones propuestas en los tres momentos; por otro lado, fueron muy constantes en el uso de los modelos explicativos y no se evidenció innovaciones en estos, por consiguiente, se prueba la variedad de los modelos explicativos usados en los estudiantes sobre los circuitos eléctricos.
Respecto a los niveles argumentativos caracterizados en los modelos explicativos, se observa que la constancia en el desarrollo de textos argumentativos de nivel 2 en los estudiantes, de tal manera que, con el enriquecimiento de sus modelos explicativos, cambiaron de un nivel argumentativo 1 a un nivel argumentativo 2 y en algunos casos a un nivel 3, al elaborar párrafos argumentativos conformados por varios componentes. En todos los modelos explicativos usados se identifica ese nivel argumentativo, a través de la elaboración en sus respuestas escritos argumentativos, conformados por conclusiones y otros componentes como datos, justificaciones y ejemplificaciones, mejorando sus procesos argumentativos mediante el desarrollo de las actividades propuestas en la unidad didáctica.
La intervención didáctica a través del diseño y aplicación de la üD como estrategia de enseñanza y aprendizaje, demuestra unos cambios importantes en la estructura argumentativa de los estudiantes, logrando un avance significativo en la manera de entender los fenómenos científicos. Por consiguiente, la relación de la argumentación y los modelos explicativos se pudo generar debido a diversos factores. Primero, las actividades estuvieron diseñadas para promover la argumentación sobre el concepto de circuito eléctrico; segundo, la implementación de actividades de argumentación individual antes de las grupales; tercero, la co-construcción de argumentos en las discusiones grupales, donde se logró evidenciar como la argumentación al articular datos, conclusiones, justificaciones y refutaciones con la evaluación de los modelos, ha servido para establecer lo que hoy se conoce como "los modelos de la ciencia" (Aleixandre et ál., 2013). Estos, pueden explicar situaciones problema como los que ocurren en los circuitos eléctricos.
La investigación desarrollada confirma la afirmación que promover las prácticas argumentativas en el aula de ciencias, conlleva reconocer que la argumentación, además de ser una actividad social, puede cualificar los procesos de aprendizaje de los conceptos. De ahí que, y teniendo en cuenta que los bajos niveles argumentativos identificados en los estudiantes están relacionados con los modelos explicativos alejados o incompletos de los modelos científicos, al abordar la enseñanza de un concepto es fundamental reconocer la estructura que de él tienen los estudiantes y diseñar las estrategias más asertivas para intervenirlas y aportar aspectos de orden conceptual que enriquezcan sus argumentos.
Recomendaciones
Como resultado de la investigación, se recomienda trabajar con estrategias de fortalecimiento en los procesos de enseñanza y aprendizaje de las ciencias a partir de la epistemología del concepto y el pensamiento crítico con sus dimensiones, en el caso de esta investigación la argumentación, que permitan avanzar en la construcción de argumentos, a partir de actividades explicitas sobre la enseñanza de los procesos argumentativos y las características de los textos argumentativos, para que los estudiantes logren llegar al nivel 4 y 5 de la argumentación de Simon, Erduran y Osborne.