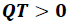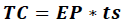INTRODUCCIÓN

La trazabilidad juega un papel importante en las cadenas de suministro de alimentos, ya que se relaciona directamente con su calidad y seguridad (^{Pizzuti et al. 2017}), permite garantizar la inocuidad y lograr confianza del consumidor (^{Aung & Chang, 2014}), además promueve el desarrollo de una gestión eficaz de la cadena de suministro (^{Dandage et al. 2017})y permite identificar el histórico, la ubicación y la ruta de un producto o un lote de productos, a través de esta (^{ICONTEC, 2000}).

En la gestión logística de la cadena de alimentos y de agricultura, se han identificado problemas de trazabilidad en los alimentos (^{Bosona & Gebresenbet, 2013}). Según ^{Rong & Grunow (2010)}, la trazabilidad recibe menos atención en la literatura en temas relacionados con la planeación de la producción y la distribución, resultando relevante que los investigadores incluyan estos temas, para generar soluciones pertinentes en este sector.

En particular, ^{Hobbs (2016)} analizó las implicaciones de trazabilidad en cadenas de suministro de carne y ^{Ding et al. (2015)} encontraron que se han realizado esfuerzos en los supermercados de China, por incrementar la trazabilidad en sus cadenas de suministro. Asimismo, ^{Narsimhalu et al. (2015)}, exploraron la influencia de los factores de trazabilidad en el desempeño de las cadenas de suministro de lácteos en Australia.

Por otro lado, incluir aspectos de trazabilidad en los sistemas de producción genera impactos económicos y operativos en las organizaciones (^{Wang et al. 2010}). En relación con el análisis de costos de trazabilidad, ^{Asioli et al. (2014)} realizaron un análisis de regresión lineal, para determinar la relación existente entre los niveles de trazabilidad, los costos y los beneficios reales y esperados de la rastreabilidad en la cadena de suministro de la pesca italiana, concluyendo que, una mayor amplitud de la trazabilidad, incrementa los costos.

En la literatura, se encuentran investigaciones en las que se desarrollaron modelos matemáticos, para tratar la trazabilidad en cadenas de suministro, como lo es el caso de ^{Grillo et al. (2017)}, quienes presentan un modelo matemático para cadenas de suministro de frutas, como la naranja y la mandarina, donde buscan maximizar dos objetivos: el beneficio total y la frescura media del producto.

^{Gautam et al. (2017)} desarrollaron un modelo de programación no lineal, que considera la minimización de costos en una cadena de suministro de kiwis, incluyendo los costos de responsabilidad en la ocurrencia de contaminación, considerando la trazabilidad, como la implementación de la tecnología de identificación de radio frecuencia.

En relación con los procesos de producción, ^{Rong & Grunow (2010)} desarrollaron un modelo de planificación de la producción y la distribución de alimentos, que permitiera controlar la dispersión, considerando la potencialidad de recolectar los productos del mercado, el impacto en los clientes y los esfuerzos logísticos que implica.

^{Comba et al. (2013)} y ^{Wang et al. (2010)}, buscaron identificar una relación entre la trazabilidad y la definición de tamaño de lote. Por un lado, ^{Comba et al. (2013)} propusieron un modelo matemático para la gestión de la trazabilidad de los productos a granel durante la producción, el almacenamiento y la entrega, proporcionando la definición de lotes en términos de su composición y tamaño. Por su parte, ^{Wang et al. (2010)} presentaron un modelo de programación no lineal entera mixta, para determinar el tamaño de lote de producción, incorporando el costo potencial de retirar el producto del mercado asociado a la trazabilidad, sin considerar que, en este tipo de industrias, se presentan listas de materiales para los productos elaborados, que incluyen diferentes tipos de materias primas, en distintas cantidades.

Según lo presentado anteriormente, la definición del tamaño de lote de producción tiene una relación estrecha con la trazabilidad que se requiere para el producto. Por tanto, es importante incluir elementos de la trazabilidad en las decisiones orientadas a la determinación del tamaño de lote de producción; en otras palabras, para establecer la trazabilidad de los lotes de materia prima que se requieren para un lote de producto terminado es necesario definir cuál será el tamaño de este lote, debido a que definirá la cantidad de lotes de materia prima requeridos, que incidirán en la determinación de la trazabilidad.

Definir un tamaño de lote de producto terminado grande representa incluir gran cantidad de lotes de una misma materia prima, que pueden provenir de diferentes proveedores con diferentes procesos y niveles de riesgo en la calidad, lo que aumentará el esfuerzo para realizar la trazabilidad; mientras que definir tamaños pequeños de lote de producción, representa incluir un solo lote de una misma materia prima, lo que significa simplificar el esfuerzo a la hora de realizar la trazabilidad.

De lo anterior, se puede decir, que dada la relación entre tamaño de lote de producto terminado y el esfuerzo que se debe hacer para realizar la trazabilidad a los lotes de materia prima, es necesario establecer una estrategia, que permita definir el tamaño de lote de producto terminado, considerando el impacto de la trazabilidad.

Tal como lo plantea ^{Wang et al. (2010)}, el costo de retirar productos del mercado representa una estrategia interesante para relacionar la trazabilidad y la definición de tamaño de lote de producto terminado, ya que la trazabilidad tiene como uno de sus objetivos garantizar la inocuidad de los productos; una mejor trazabilidad, se debe reflejar en menores deterioros de productos finales y, a su vez, en menores costos de retirar productos en el mercado.

Si el tamaño de lote de producto terminado es tan grande que, para cada una de las materias primas requeridas se deban emplear diferentes lotes que provienen de diferentes fuentes, no solo se dificulta la trazabilidad, sino que los riesgos de calidad que se puedan tener con los proveedores se acumulan y esto hace que aumente la posibilidad de que se presenten problemas de calidad con el aumenta el costo de retirar productos del mercado.

Por otro lado, otro elemento que agrega complejidad a la determinación de la trazabilidad es el tamaño de lote de envío al cliente, ya que establece una relación con el tamaño de lote de producción, la cantidad de inventario de producto terminado y la gestión de la vida útil de los productos finales. En tal sentido, tamaños de lote grandes de producto terminado, en presencia de tamaños de envío pequeños a los clientes, producen un inventario alto, lo que incrementa la posibilidad de que el producto salga al mercado con una menor vida útil; esto se reflejará en costos por retirar productos del mercado.

Con estos elementos y sabiendo que los materiales son fundamentales para el cálculo de requerimientos de materia prima, la presente investigación tuvo como objetivo desarrollar una metodología que permita determinar el tamaño de lote, considerando la trazabilidad, representada en el costo de retirar productos del mercado, en un sistema de producción contra inventario, con tamaño de lote de entrega discreto definido por el usuario y con listas de materiales explicitas, para el cálculo de las necesidades de materia prima.

Se hace una extensión al trabajo de ^{Wang et al. (2010)} y como principales aportes se tienen: se adicionan el concepto de lista de materiales, para la determinación de los requerimientos específicos de materia prima, para cada lote de producto terminado y se considera la utilización de diferentes lotes del mismo tipo de materia prima, provenientes de diferentes proveedores, lo que con lleva a precios distintos y diferentes niveles de calidad.

En este documento, se tiene la siguiente estructura: inicialmente, la metodología utilizada para establecer el modelo de programación de producción, la definición y descripción del modelo y, posteriormente, un análisis de los resultados junto con los respectivos escenarios, para el análisis de sensibilidad y las conclusiones.

MATERIALES Y MÉTODOS

Como estrategia metodológica, se desarrolló un modelo matemático de programación no lineal entero mixto, que permite incluir las variables productivas y los elementos de trazabilidad en la toma de decisiones, alrededor del tamaño de lote de producción. A continuación, se presentan las generalidades del modelo y los detalles específicos de la formulación.

Definición del modelo propuesto

Generalidades del modelo. Las extensiones consideradas son:

Una vez definidas las variables y los parámetros, se representa en la figura 1, el problema que se aborda al definir un tamaño de lote de producción, considerando la trazabilidad, su dependencia con los diferentes lotes de materias primas de diversos proveedores y su relación con el tamaño de lote de envío de producto terminado al cliente.

Se tiene que en el proceso de producción, se debe definir el tamaño de lote de producción QT, el cual, estará compuesto por la suma de los requerimiento de materia prima rk_k provenientes de la lista de materiales; cada cantidad de materia prima tipo k requerida Qk_k podrá provenir de lotes de diferentes proveedores l_ik y cada lote tendrán una capacidad cpi_ik, en la medida en que requiera utilizar materia prima de diferentes proveedores, por la capacidad que estos tengan para completar el total de materia prima tipo k (Q_k). Se activa la variable binaria YI_ik, por cada lote i que se requiera de la materia prima k, es decir, que la cantidad requerida de cada lote dependerá de la capacidad que tenga para completar el total de materia prima del mismo tipo.

Entonces, la sumatoria de la variable binaria YI_ik, indicará la cantidad de lotes que se requieren para producir el lote de producción QT, de tal modo que, entre mayor sea el tamaño de lote producción y menor sean las capacidades de los lotes de materia prima, se incrementará la dispersión y, con esto, la dificultad para realizar trazabilidad.

Por otro lado, cuando ya se tiene el lote de producto terminado QT y se requiere enviar al cliente, se establece un tamaño de lote de envío xp, que depende de las condiciones del contrato acordadas o de condiciones de transporte, entre más pequeño sea este lote de envío, mayor será el número de envíos para el cliente y, a su vez, mayor será el periodo que se tenga el inventario en la planta, lo cual, incrementa el costo de inventario y reduce el tiempo de vida útil que tendrá el producto, después de salir de planta.

Modelo propuesto

Función objetivo

Restricciones:

En el modelo propuesto, la ecuación E1 representa la función objetivo y está conformada por los costos totales de: alistamiento, materia prima, retirar productos del mercado, posesión e inventario de producto terminado deteriorado u obsoleto. Las ecuaciones E2 y E3 permiten determinar el requerimiento de la materia prima k. Las ecuaciones E4, E5 y E6 permiten fijar el tamaño de lote de producto terminado. La E7 es funcional y permite activar la variable binaria de uso del lote i de una materia prima k. Las ecuaciones de E8 a E11 representan, respectivamente, los costos totales de: inventario, alistamiento, de retirar y de materia primas. Las ecuaciones de E12 a E15 permiten establecer el número de pedidos durante el periodo de escases y la cantidad faltante de producto terminado. Las ecuaciones de E16 a E18 determinan el costo de obsolescencia. Las ecuaciones de la E19 a E21 permiten definir el tiempo de ciclo. La ecuación E22 permite hacer el cálculo de la dispersión y E23 son las de tipo de variables.

Descripción detallada del modelo. A continuación, se detallan los elementos principales y diferenciadores de modelación considerados en esta propuesta. Se iniciará con la definición del tamaño de lote, a partir de la lista de materiales, posteriormente, con el cálculo de la dispersión del tamaño de lote; después, la definición del período de tiempo de ciclo y el cálculo del inventario promedio de producto terminado y, finalmente, la definición del envío del tamaño de lote.

Definición del tamaño de lote de producción del tipo de producto terminado. En el modelo propuesto, la cantidad requerida de materia prima de tipo k, QK _k , es igual a la multiplicación de la cantidad de lote de producto terminado ( QT ) y el requerimiento de cada materia prima de tipo k:

La cantidad de materia prima de tipo k debe ser igual a la sumatoria de materia prima de tipo k aportada por todos los lotes i:

El tamaño de lote de producto terminado es igual al producto del número de envíos de producto terminado por la cantidad de producto terminado pactada con el cliente por entrega:

Las siguientes ecuaciones son restricciones del tamaño de lote de producción:

La siguiente ecuación expresa que la variable YI _ik es igual a 1, si QI _ik es diferente de cero.

Cálculo de la dispersión. La dispersión del tamaño de lote de un sistema corresponde a la suma de todas las materias primas de la dispersión descendente y de todos los productos terminados de la dispersión ascendente

La dispersión descendente corresponde al número de lotes de producto que contiene partes de un lote de materia prima y la dispersión ascendente, al número de diferentes lotes de materia prima utilizadas para producir un lote de producto.

En la siguiente ecuación, se representa la dispersión del lote de producción.

Definición del periodo de tiempo de ciclo. El tiempo de ciclo, se define como:

Definición del inventario promedio del producto terminado. Hay dos partes de inventario consideradas en el modelo: el inventario de producto terminado acumulado durante el tiempo de producción, como se puede observar en el área triangular en la figura 2 y el inventario de producto terminado, listo para entrega, representado en el patrón en escalera en la figura 2.

El inventario promedio, se puede expresar como la siguiente integral evaluada entre 0 y T:

El primer componente la ecuación del IP , que se representa como A1 , calcula el nivel de inventario promedio de productos terminados acumulados durante la producción.

La base del triángulo sombreado de la figura 2 está dada por QT/tp, que es el tiempo necesario para reponerlo. La altura del triángulo es QT ; con esto, se puede definir el inventario como:

Integrando, se obtiene:

El segundo componente, la ecuación del IP , que se representa como A1 , calcula el nivel del inventario listo para entrega (patrón en escalera) y es la sumatoria de la cantidad exacta para envíos individuales de producto terminado.

El área del inventario de producto terminado listo para entrega, se puede expresar como:

Reemplazando en el segundo término del inventario promedio, se obtiene:

Consolidando, se obtiene:

Definición del número de envíos requeridos durante el periodo de escasez de demanda del producto terminado. Este es igual al número de envíos totales en el ciclo de producción de un lote de productos terminado menos el número de envíos en el periodo normal.

Definición de la cantidad faltante de producto terminado para satisfacer la demanda. Una vez se ha definido el número de envío en el periodo de escases ET , la cantidad faltante se obtiene así:

El costo de obsolescencia. Se define como la penalización que reciben los fabricantes, debido a que los productos no cumplen con los requerimientos fijados () en el contrato y se define como:

La anterior expresión, se realiza en el modelo a través de las siguientes ecuaciones.

En este caso, si el número de envíos de producto terminado EP supera el número de pedidos que se podían entregar dentro de la vida útil, YY toma el valor de uno, indicando que algunos de los envíos llegarán por fuera de la vida útil, generando, con esto, la activación del costo de obsolescencia.

RESULTADOS Y DISCUSIÓN

Validación del modelo: Para la validación del modelo propuesto, se utilizó un caso de estudio de producción de salchichas, en el que se consideraron, como materias primas, cinco tipos de carnes requeridas para el producto; en la figura 3, se presenta la lista de materiales, donde se visualizan los flujos y los diferentes lotes para un mismo tipo de materia prima y el requerimiento de la materia prima de tipo k, en un producto terminado. Los otros parámetros generales del modelo, se presentan en la tabla 1.

Para la solución del modelo, con el caso de estudio, se utilizó, como herramienta de implementación, el software Lingo® Versión 8.0, en donde se cargaron los parámetros y las restricciones establecidas, se generaron 79 variables y 64 restricciones.

La función objetivo dio como resultado $128.769.700; se pudo identificar, que los costos de materias primas tienen mayor participación en el costo total, puesto que el coeficiente de probabilidad de retirar el producto terminado tiene un historial de 0,15; el costo potencial de retirar productos del mercado es de $9.754.875; el costo de ordenar es de $655.500, por lo que el número de órdenes enviadas, que está dado por dm/QT, es de 6,9.

Respecto a las otras variables productivas, el costo de mantener es de $278.571 y, por último, el costo de obsolescencia es igual a cero, debido a que no se presentó ningún envío durante el periodo de escasez y, por consiguiente, ningún producto llega fuera del ciclo de vida, pactado con el cliente.

El tamaño de lote es 500 unidades, que serán entregadas a través de envíos de cantidades fijas de producto terminado de 50 unidades cada día, aproximadamente. Con los resultados del modelo fue posible identificar que predomina el costo de las materias primas frente al riesgo de utilizar un lote i de materia prima tipo k, que se encuentra asociado al costo potencial de retirar producto del mercado.

Para analizar el impacto de la consideración de la trazabilidad en las variables productivas asociadas al tamaño de lote de producción, se propusieron 4 escenarios, con el fin de realizar un análisis de sensibilidad de los principales parámetros y los cambios en las variables del modelo. La descripción de los escenarios es la siguiente:

Escenario 1: Incremento en xp : En este escenario, con el propósito de identificar el impacto que tiene el tamaño de entrega xp en las variables de producción y en la definición del tamaño de lote, se realizaron variaciones de dicha entrega. Para ello, se evalúa el modelo, incrementando el tamaño xp en unidades de 5 cantidades hasta 100 unidades, manteniendo constante los demás parámetros.

Escenario 2: Variación en ri _ik : Dado que el parámetro riik está relacionado directamente con la dispersión DL de la ecuación E22 del modelo, se propone realizar variaciones, para identificar el impacto de la dispersión en la variables tamaño de lote y en el costo de retirar el producto. Para ello, se fijaron todos los parámetros, exceptuando los riesgos de cada lote i disponible de materia prima de tipo k. Los valores de ri_ik que se consideraron para el cálculo inicial del estudio de caso, se toman como medida para realizar el análisis de este escenario. Cada valor se multiplica por un porcentaje, que va desde 5, incrementándose en 5 unidades porcentuales, hasta llegar al 100 por ciento.

Escenario 3: Variación en λ: El coeficiente de retirar productos del mercado, λ se relaciona con la trazabilidad en la ecuación E10, por ello, con el propósito de identificar el efecto de la consideración de la trazabilidad en el costo de retirar y, por ende, en la definición del tamaño de lote, se realizaron variaciones en λ; para ello, se tomaron valores desde 5 por ciento, incrementándose en 5 unidades porcentuales, hasta alcanzar el 100 por ciento.

Escenario 4: Variación en cpi_ik: En la ecuación E7, se identifica que la capacidad de los lotes de materia prima cpiik se relaciona indirectamente con la trazabilidad, ya que, entre más pequeña sea la capacidad de los lotes, más veces se activa la variable YI_ik, en tal sentido, para identificar el impacto que tiene la trazabilidad en el tamaño de lote se realizaron variaciones en los valores de cpi_ik multiplicándolos por un porcentaje que va desde 5, incrementándose en 5 unidades, hasta llegar al 100 por ciento.

Análisis de sensibilidad: Escenarios

Escenario 1. Incremento en xp: Entre mayor sea la cantidad de producto terminado enviado por cada entrega, el tamaño de lote QT se incrementa en múltiplos del valor de xp y se tiene una tendencia creciente en el costo total.

En la figura 4, se presentan los resultados de los cuatro escenarios planteados en esta investigación. En la figura 4a, se presentan las variaciones en xp frente a la dispersión del lote de producción (DL) y el costo total, entre mayor sea la cantidad del tamaño de producto terminado xp y, por ende, de QT, la tendencia de la dispersión del lote es creciente, puesto que se necesitan mayor número de lotes de un mismo tipo de materias primas, para cumplir con la orden de producción.

Escenario 2. Variación en ri _ik : Cuando los riesgos de los lotes de materia prima se cambian, se puede determinar que, entre mayor sea el riesgo, mayor será el costo potencial de retirar productos del mercado y, por ende, el costo total de la producción; sin embargo, dado que de la vida útil del producto terminado y de la vida útil contratada restringen el tamaño de lote, este se mantiene constante, generando que los otros costos no varíen, atenuando el efecto del costo de retirar productos (Figura 4b).

Escenario 3. Variación en λ: En la figura 4c, se puede observar que, entre mayor sea el coeficiente de retirar del mercado un producto λ en específico, mayor será el costo potencial de retirar productos del mercado (CR).

Asimismo, se puede identificar que el costo total del modelo de planeación de producción se comporta de manera análoga al costo potencial de retirar productos del mercado.

Escenario 4. Variación en cpi _ik : De acuerdo con la figura 4d, se puede observar que, para un mismo tipo de materia prima, cuando la capacidad de los lotes disponibles es baja, la dispersión del lote se ve afectada, ya que se requieren más lotes de materia prima para cumplir con los requerimientos y esto implica una mayor dispersión.

El desarrollo y el análisis de los escenarios permiten plantear que ciertos aspectos de la trazabilidad, tales como la homogeneidad de las materias primas, tiene una gran incidencia dentro de la definición del tamaño de lote de producción, por lo que su variabilidad presenta un impacto importante dentro del costo potencial de retirar productos del mercado.

La inclusión de la dispersión en el cálculo del tamaño de lote es un elemento bastante útil, puesto que permite conocer la dimensión de las relaciones que hacen parte del proceso de fabricación y esto da una representación de la complejidad que puede tener el proceso de retirar productos del mercado, dada una eventualidad. Asimismo, se pudo observar que el incremento en la dispersión no es recomendable, dentro de la definición del lote de producción.

A partir de los análisis, se logró identificar que un elemento clave dentro de la definición del tamaño de lote es una adecuada selección de la materia prima y, por ende, de los proveedores, ya que, minimizando el riesgo y la variabilidad de cada uno, se obtiene uniformidad y calidad de los productos generados, lo cual, se refleja en la diminución del costo potencial de retirar productos del mercado.

El desarrollo de problemas de optimización, como el presentado, desde el punto de vista académico, logra ser bastante interesante, puesto que se está adaptando y desarrollando una nueva perspectiva para dar respuesta a una nueva exigencia del mercado; sin embargo, gran parte de los resultados de estas prácticas dependen de la capacidad que tengan las compañías de implementar y gestionar un sistema de trazabilidad.

La inclusión de las listas de materiales permitió una definición más precisa de los lotes de materia prima, a partir del lote de producto terminado definido, lo cual, trasfiere, de manera directa, el tamaño de lote de producto en la dispersión y, este, a su vez, en el costo de recoger productos en el mercado, que representa la trazabilidad en el problema de toma de decisiones.