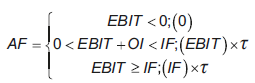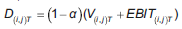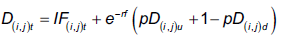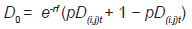1. Introducción
El modelo de descuento de flujos de fondos es uno de los métodos de mayor difusión y uso en la valuación de empresas. Presenta diferentes variantes según el tratamiento otorgado al costo del capital y la manera en que son exteriorizados los ahorros fiscales, a saber: a) Costo Capital Promedio Ponderado (CCPP, o WACC por su sigla en inglés Weighted Average Cost of Capital), b) flujos de fondos a capital, y c) valor presente ajustado (APV, por su sigla en inglés Adjusted Present Value) (Ruback, 2002; Damodaran, 2006; Booth, 2007; Fernández, 2014). En su versión tradicional, el descuento de flujo de fondos presenta cuestiones controvertidas, especialmente el tratamiento de los ahorros fiscales producto del uso de la deuda financiera y el impacto que tienen en el valor de la firma el apalancamiento financiero y los escenarios contingentes de continuidad o liquidación. El modelo de descuento de flujos de fondos explica el valor de la empresa de una manera sencilla pero poco realista, a partir de una relación funcional lineal originada por ahorros fiscales positivos y flujos de fondos esperados promedios, estos últimos resumiendo potenciales escenarios de la empresa.
Estimar el valor actual de los ahorros fiscales proyectados sobre una base determinística, tiene poco que ver con la realidad de los negocios, ya que su existencia se encuentra condicionada por: a) resultados imponibles positivos, b) impuesto operativo a las ganancias mayor o igual que el valor de los ahorros fiscales, c) intangibilidad o variabilidad de las normas tributarias. Asimismo, para la estimación del valor intrínseco de la firma y el capital propio, el modelo debe reformularse e incorporar los escenarios contingentes de continuidad y liquidación. Los escenarios son: (a) flujos de fondos libres superiores a los pagos de deuda, su consecuencia es la continuidad de la firma, (b) insuficiencia de flujos de fondos libres, que deriva en la liquidación automática de la empresa y cancelación de los pasivos con los activos disponibles, descontados los costos de quiebra.
Atendiendo a las consideraciones precedentes, este trabajo desarrolla un modelo de valuación de la firma y el capital propio, incorporando la naturaleza contingente de los ahorros fiscales condicionados a los potenciales escenarios de continuidad y liquidación de la firma. Para ello se propone valuar ahorros fiscales asemejando sus flujos a una cartera de opciones, siguiendo el modelo propuesto por Velez Pareja (2016). En relación a la incorporación de los escenarios contingentes, son adaptados los modelos binomiales contenidos en los trabajos de Broadie y Kaya (2007) y Milanesi (2014). La lógica de estos trabajos reside en el clásico concepto de considerar el valor del patrimonio neto como una opción de compra, pero a diferencia de las publicaciones indicadas y para presentar un marco coherente con el tratamiento de los ahorros fiscales, se supone que el valor de la firma sigue un proceso estocástico geométrico browniano (Brandao, Dyer y Hahn, 2005; Smith, 2005), mientras que los resultados operativos antes de impuestos son explicados por un proceso estocástico aritmético browniano.
En lo que resta del documento, la estructura del trabajo es la siguiente: en la sección dos se presenta el marco teórico en donde se exponen el conjunto de ecuaciones destinadas a cuantificar el valor del ahorro fiscal asimilado a una cartera de opciones, y el modelo binomial de valuación condicionado a resultados de liquidación. La tercera sección desarrolla el abordaje metodológico y, a continuación, se presentan los principales resultados. Se utilizó el análisis de sensibilidad para diferentes niveles de apalancamiento financiero con el fin de comparar los resultados obtenidos entre el modelo tradicional y el desarrollo propuesto. Finalmente, se presentan las principales conclusiones.
2. Marco teórico: modelo binomial de valuación en estados contingentes
En esta sección se procederá a derivar y exponer el conjunto de ecuaciones que explican las relaciones contingentes entre valor, ahorros fiscales y efectos del endeudamiento frente a escenarios de insolvencia y continuidad de la empresa. A partir de lo anterior, se conforma la propuesta para la determinación del valor de la empresa y el patrimonio neto frente a escenarios contingentes.
2.1. El valor actual del ahorro fiscal como una cartera de opciones
Tradicionalmente, el valor del ahorro fiscal para un periodo se estima de la siguiente manera.
Donde IF representa la magnitud de intereses financieros computables y τ la alícuota marginal del impuesto. El valor actual de los sucesivos ahorros fiscales es igual a
La ecuación (2) plantea uno de los principales focos de debate entre los académicos y practicantes. En este caso, r es la tasa a la cual son actualizadas las corrientes futuras de ahorros fiscales. Ahora bien, la doctrina ha desarrollado un importante debate relativo a que tasa de actualización debe ser utilizada, el cual a continuación será sintetizado. Existen dos posiciones extremas: a) Modigliani y Miller (1963) proponen actualizar los ahorros fiscales a la tasa libre de riesgo, b) Miles y Ezzell (1980, 1985) proponen actualizar los ahorros en el primer año al costo de la deuda y los años subsiguientes a las tasa del costo del capital para una firma desapalancada k u . También hay autores con posturas ecléticas entre las posiciones extremas indicadas, entre ellos Taggart (1991), Inselbag y Kaufold (1997), Tham y Wonder (2001), Tham y Velez Pareja (2001), Tham y Wonder (2002), Booth (2002), Farber, Gillet y Szafarz (2006), Cooper y Nyborg (2006), Oded y Michel (2007), Velez Pareja (2016). Los anteriores consideran que el valor de los ahorros fiscales es condicionado por la estructura objetivo de capital de la firma, entendiendo por estructura objetivo al mantenimiento de un ratio de mercado en relación al valor de la deuda (posición b) (Miles y Ezzell, 1980, 1985); o en otro extremo, mantener un valor actual fijo de deuda (posición a) (Modigliani y Miller, 1963).
Una tercera posición es la que plantea Fernández (2014). Este autor sostiene que las posiciones anteriores son apropiadas para firmas irreales, ya que la primera se emplea en el caso de empresas con un valor actual de deuda fijo y la segunda cuando el valor de la deuda se calcula como un múltiplo del valor de mercado del patrimonio de la firma. Su posición reside en calcular un valor intermedio de estructura de capital objetivo a partir de ratios de endeudamiento calculados a valor de libros. Se apoya en la evidencia encontrada en trabajos empíricos donde el ratio de endeudamiento a valor de libros se mantiene constante, igual que su ratio de endeudamiento a valores de mercado. Esto hace que tenga mayor sentido caracterizar estructuras de capital en el largo plazo a partir de valores de libros fijos, en lugar de valores de mercado. En palabras de Copeland, Koller y Murrin (2000, p.482)“la literatura financiera no provee una clara respuesta en relación a cuál tasa de descuento para los ahorros fiscales de intereses es la teóricamente correcta”.
Siguiendo a Vélez Pareja (2016), se propone desarrollar e incorporar en el modelo de valuación la determinación del valor del ahorro fiscal aplicando la teoría de opciones, a partir del modelo binomial. Sus ventajas consisten en considerar en la determinación de los ahorros fiscales los estados contingentes. Además, evita el debate respecto de la tasa de actualización a ser utilizada, ya que en el enfoque de opciones el riesgo es tratado en los flujos de fondos, reservándose la tasa libre de riesgo simplemente para reflejar el valor tiempo del dinero.
Con tasas de deuda fijas y legislación tributaria estable, la única fuente de riesgo está dada por la variabilidad de los resultados. Entonces, los ahorros fiscales dependen de: a) resultados operativos positivos (EBIT), b) resultados mayores o iguales al valor del ahorro fiscal, en caso contrario, su deducción tiene como techo el valor de la ganancia operativa imponible. Los escenarios contingentes indicados se expresan a continuación:
De esta forma, las ecuaciones 1 y 2 serán correctas siempre y cuando se verifique las condiciones a) y b), sujeto a que los riesgos fiscales sean replicados por los precios de los activos financieros negociados en el mercado de capitales. No obstante, las situaciones contingentes de indicadas en la ecuación 3, son abordadas por la teoría de opciones reales. En este sentido, el valor de los ahorros fiscales se asemeja a una cartera de opciones, la cual se encuentra constituida por una posición larga y corta correspondiente a una opción de compra americana, conocida como estrategia de caps (techos). En esta cartera, el subyacente lo constituye la base imponible del impuesto, es decir, los resultados operativos S t = EBIT t . Por lo tanto, el valor del ahorro fiscal es igual a la suma algebraica entre el valor de una posición larga en un call americano C(O) t , con precio de ejercicio X = 0 y una posición corta sobre un call C(IF) t con ejercicio igual al ahorro fiscal computable
X = IF × τ. La idea intuitiva reside en suponer que la empresa ejerce el call siempre que los resultados sean mayores que cero (condición a, ecuación 3). La posición corta actúa como un techo igual al valor del ahorro fiscal en el caso que los resultados sean mayores que los intereses (condición b, ecuación 3). Las canastas de opciones son del tipo americano, ya que son ejercidas periódicamente al cierre del ejercicio fiscal.
Por lo tanto, los flujos de fondos asociados a los valores terminales (T) de la cartera surgen de las siguientes condiciones:
Flujo 1: no ejercicio, inexistencia de ahorro fiscal: EBIT < 0; (0).
Flujo 2: ejercicio de la opción valor de la opción impuesto operativo a las ganancias: C (0)T = max (EBIT × τ ; 0 ). El ejercicio de la posición larga va desde 0 < EBIT < IF ; (EBIT) × τ hasta infinito.
Flujo 3: venta de la opción de compra (ahorro fiscal): C (IF) T = min((EBIT) × τ; (IF) × τ ). El ejercicio de la posición se activa desde EBIT + 0I ≥ IF; (IF) × τ con el techo pertinente.
El valor de la cartera es la diferencia entre el impuesto a las ganancias proyectado calculado sobre el resultado operativo, y el impuesto a las ganancias calculado sobre el resultado neto de intereses, condicionado a los flujos y ejercicios precedentes C(AF) T = C (0) T − C(IF) T . La expresión sintética correspondiente al valor terminal de la opción es:
En la proyección del EBIT, al suponer valores positivos como negativos, es empleado el proceso aritmético browniano1. Seguidamente es aplicado el clásico modelo binomial (Cox, Ross y Rubinstein, 1979)2. Para ello es importante definir para todo periodo t = 1...T y nodo (i, j) de la rejilla binomial, la expresión correspondiente al valor actual de los ahorros fiscales, así:
Donde el término V A T-t+1 e -rt representa el valor del ahorro fiscal del periodo T − t + 1 actualizado a la tasa libre de riesgo.
En cada nodo del instante T se supone continuidad y determinismo en el valor del ahorro fiscal estimado, a partir de la ecuación 4. Entre el intervalo de tiempo de los nodos T-t, el valor del ahorro fiscal se integra con el valor de la opción C (AF) T , y el valor actual de los ahorros fiscales esperados en T-t+1 para (i,j) VAF T-t(i,j)e-rt. Empleando probabilidades neutrales al riesgo3 en cada nodo (i,j) de la rejilla, se determina el ahorro fiscal con la lógica de un cap americano, en este caso, con techo igual a IF × τ,
Si se procede a notar a la cartera de opciones como  , la expresión queda planteada de la siguiente manera:
, la expresión queda planteada de la siguiente manera:
2.2. El modelo binomial, posibilidades de liquidación y el valor del ahorro fiscal
En esta sección se integran las ecuaciones empleadas para estimar el valor del ahorro fiscal al modelo binomial de valuación, con posibilidades de liquidación o continuidad (Broadie y Kaya, 2007; Milanesi, 2014), como propuesta integradora para estimar un valor de empresa, condicionado a la naturaleza contingente de las variables analizadas.
En este caso se supone que los flujos de fondos proyectados residuales deben ser suficientes para atender los pagos de deuda, en su defecto se procede a cancelar los intereses de la deuda y se procede a liquidar el patrimonio neto. Consecuentemente, el valor de la firma es el valor actual del EBIT, condicionado a los escenarios de liquidación y valor actual de los ahorros fiscales futuros. Por lo tanto, el valor del patrimonio de los propietarios es el valor actual de los flujos residuales incorporando los contingentes escenarios de liquidación y valor actual de los ahorros fiscales futuros. En los escenarios de liquidación no se esperan ahorros fiscales y se asume que no se pueden trasladar quebrantos tributarios a otros sujetos. Se debe tener presente que el modelo numérico binomial se basa en el desarrollo el trabajo de Milanesi (2014). En el anexo es planteado el desarrollo matemático del mismo.
De esta forma, existen tres momentos condicionados por escenarios de insolvencia o continuidad. El primero es el valor terminal en el instante T, el segundo está dado por el intervalo (t<T; t≥1), finalmente el valor actual es en el instante t=1 →0. El valor de la firma, condicionado en el horizonte T presenta el siguiente conjunto de ecuaciones para el caso de continuidad:
En el caso de liquidación las ecuaciones quedan planteadas como:
En los intervalos temporales intermedios, es decir (t<T; t≥1), las ecuaciones para valorar la empresa en situación de solvencia son:
La liquidación de la firma es capturada por las siguientes expresiones,
Finalmente, el valor de la firma y capital propio en t=0 es obtenido una vez calculados los valores finales (T, punto (I)) e intermedios (t<T; t> punto (II)), condicionados por los escenarios (continuación-liquidación). Se trabaja a partir del periodo de tiempo t=1 hasta t=0; (t=1 →0),
En esta instancia se obtiene el valor esperado de la firma y del capital propio condicionado a situaciones de insolvencia e incorporando contingentemente valores de ahorro fiscal.
3. Metodología
El modelo desarrollado formalmente en el apartado precedente, será analizado aplicando el enfoque metodológico de estudio de casos. Este no debe confundirse con la clásica herramienta pedagógica empleada en administración conocida como análisis de casos (Castro Monge, 2010). El análisis de casos busca revisar algún aspecto concreto en la organización con vista a fomentar el debate. Por el contrario, la metodología de estudio de casos, partiendo de las relaciones teóricas contenidas en la teoría, tiene por fin establecer proposiciones teóricas destinadas a sostener y ampliar el modelo estudiado. En este caso, las relaciones se encuentran contenidas en el marco de la valuación de empresas, en particular mediante el enfoque de pagos contingentes contenidos en la teoría de opciones reales.
Para ello, se parte de una empresa hipotética cuyo EBIT asciende a valor actual de $1004, con un costo del capital (k u ) del 10%, volatilidad del resultado (σ) del 35% y tasa libre de riesgo (r) 5%. El costo financiero de la deuda se mantiene fijo en un 10%, el valor actual de la deuda asciende a $100 y la alícuota marginal de impuesto a las ganancias es del 35%. Adicionalmente, se supone que el ratio de endeudamiento se mantiene estable en términos absolutos, ascendiendo al 45% del valor intrínseco de la empresa en t=0, mientras que el valor intrínseco inicial de la firma es V=$1.000, por lo tanto D = $450. En el caso de liquidación de la empresa por insolvencia, se supone que los costos de quiebra (α) originados en la reorganización empresarial ascienden al 3% del valor de los activos, al momento de la disolución5. Además, el ratio de flujos de fondos (RFF) asciende a 10%. En la siguiente sección serán aplicados los modelos y analizados los resultados obtenidos, tanto para la determinación y valuación de ahorros fiscales contingentes, como para el modelo numérico binomial.
4. Resultados
En esta sección se presentan los principales resultados al aplicar el modelo a partir del caso hipotético enunciado en la sección anterior. Además del estudio de las relaciones funcionales, son comparados los resultados del modelo y la versión tradicional del descuento de flujos de fondos, obtenidos mediante análisis de sensibilidad sobre el grado de apalancamiento financiero.
4.1. El valor del ahorro fiscal como una canasta de opciones
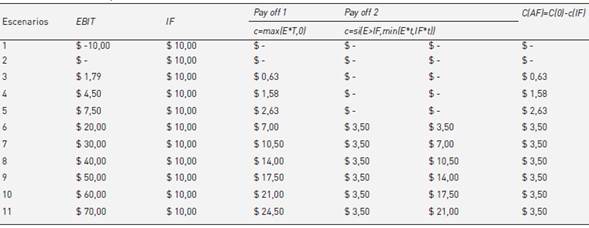
Para ilustrar el tratamiento de los ahorros fiscales como una canasta de opciones, la tabla 1 presenta el resultado de la opción sensibilizando el EBIT de la firma.
Las tres últimas columnas de la tabla 1 integran el flujo de pagos de la cartera de opciones que replica el valor del ahorro fiscal. En la cuarta columna son presentados los valores de la primer opción, C(0)T = max (EBIT × τ ; 0). La quinta columna expone la posición corta en el call, con ejercicio igual al valor de los intereses, C(IF) T = min ((EBIT) × τ ; (IF) × τ )6. Finalmente, en la sexta columna son expuestos los posibles resultados producto del ahorro fiscal. Por otra parte, surgen de la cartera de opciones la posición larga y corta sobre un call, con diferentes precios de ejercicio X 1 = O; X2 = IF . Cabe destacar que el techo de la cartera es activado por la posición corta. La figura 1 grafica el comportamiento del ahorro fiscal como canasta de opciones.
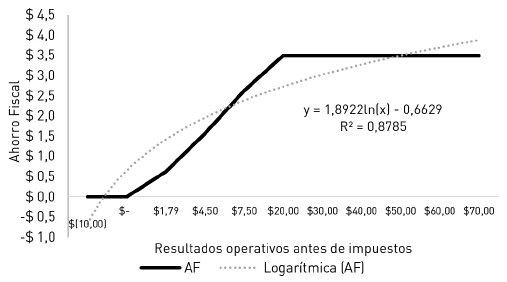
Fuente: elaboración propia.
Figura 1 Perfil de resultados correspondiente a la canasta de opciones que replica el valor del ahorro fiscal.
A continuación se desarrolla el proceso recursivo contenido en las ecuaciones 6 y 7. Para estimar el valor de los ahorros fiscales esperados, primero se debe proyectar el EBIT con un proceso aritmético browniano, aplicando el tradicional modelo binomial. En este caso, los valores correspondientes a los coeficientes de ascenso y descenso son u = e σt = 1,490 y d = e σt = 0,7046. La expresión utilizada es la siguiente7:
En la ecuación precedente, las variaciones  y
y  son constantes a lo largo del intervalo de proyección. Los resultados son expuestos en la tabla 2.
son constantes a lo largo del intervalo de proyección. Los resultados son expuestos en la tabla 2.
Tabla 2 Proyección del EBIT según proceso aritmético browniano
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ 100,00 | $ 141,91 | $ 183,81 | $ 225,72 | $ 267,63 | $ 309,53 |
| $ 70,47 | $ 112,38 | $ 154,28 | $ 196,19 | $ 238,10 | |
| $ 40,94 | $ 82,84 | $ 124,75 | $ 166,66 | ||
| $ 11,41 | $ 53,31 | $ 95,22 | |||
| $ -18,12 | $ 23,78 | ||||
| $ -47,66 |
Fuente: elaboración propia.
Posteriormente, se procedió a obtener los insumos que el modelo necesita para aplicar las ecuaciones 6 o 7, con el fin de calcular el valor del ahorro fiscal. La tabla 3 presenta los valores terminales (t=5) de la posición larga en el call con precio de ejercicio X=0.
Tabla 3 Proyección de los valores terminales en cada nodo para la posición larga en el call
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ 35,00 | $ 49,67 | $ 64,33 | $ 79,00 | $ 93,67 | $ 108,34 |
| $ 24,66 | $ 39,33 | $ 54,00 | $ 68,67 | $ 83,33 | |
| $ 14,33 | $ 29,00 | $ 43,66 | $ 58,33 | ||
| $ 3,99 | $ 18,66 | $ 33,33 | |||
| $ - | $ 8,32 | ||||
| $ - |
Fuente: elaboración propia.
La tabla 4 expone los valores terminales correspondientes a la posición corta en el call, con precio de ejercicio X=IF.
Tabla 4 Proyección de los valores terminales en cada nodo para la posición corta en el call
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 |
| $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | |
| $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | ||
| $ - | $ 12,60 | $ 12,60 | |||
| $ - | $ - | ||||
| $ - |
Fuente: elaboración propia.
Las tablas 3 y 4 presentan, en cada uno de los nodos, el evento contingente de manera desagregada. A continuación, la tabla 5 expone la rejilla con el impuesto a pagar proyectado en cada nodo.
Tabla 5 Proyección de los valores terminales correspondientes al impuesto a pagar proyectado
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ 22,40 | $ 37,07 | $ 51,73 | $ 66,40 | $ 81,07 | $ 95,74 |
| $ 12,06 | $ 26,73 | $ 41,40 | $ 56,07 | $ 70,73 | |
| $ 1,73 | $ 16,40 | $ 31,06 | $ 45,73 | ||
| $ 3,99 | $ 6,06 | $ 20,73 | |||
| $ - | $ 8,32 | ||||
| $ - |
Fuente: elaboración propia.
El valor contingente terminal correspondiente al ahorro fiscal terminal, en cada nodo (C(AF)T-t(i, j) =C(O)T-t(i, j) -C(IF)T-t(i, j)), surge por la diferencia entre los valores proyectados correspondientes al impuesto operativo (tabla 3) y el impuesto a pagar proyectado estimado (tabla 5). La tabla 6 sirve de antesala para calcular el valor actual contingente de las corrientes de ahorros fiscales aplicando las ecuaciones 6 y 7. Previamente es importante calcular los coeficientes equivalentes ciertos, p = ( e rt - d) / ( u - d) como su complemento 1- p. En este caso ascienden a p=0,4851 y 1-p=0,5148.
Tabla 6 Proyección de los valores terminales correspondientes al ahorro fiscal
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 |
| $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | |
| $ 12,60 | $ 12,60 | $ 12,60 | $ 12,60 | ||
| $ - | $ 12,60 | $ 12,60 | |||
| $ - | $ - | ||||
| $ - |
Fuente: elaboración propia.
Como todo modelo de valuación, uno de los supuestos fuertes consiste en asumir que el valor del ahorro fiscal en t(i,j)=T(i,j) sigue el comportamiento de una perpetuidad sin crecimiento . La tabla 7 presenta el valor del ahorro fiscal para cada nodo, y el valor actual de todos los nodos.
Tabla 7 Estimación del valor del ahorro fiscal
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ 210,65 | $ 238,66 | $ 252,88 | $ 252,60 | $ 252,31 | $ 252,00 |
| $ 179,51 | $ 223,28 | $ 252,60 | $ 252,31 | $ 252,00 | |
| $ 130,41 | $ 192,16 | $ 252,31 | $ 252,00 | ||
| $ 59,48 | $ 128,90 | $ 252,00 | |||
| $ - | $ - | ||||
| $ - |
Fuente: elaboración propia.
En este caso, el valor actual de los ahorros fiscales asciende a $210,65, una cifra sensiblemente superior a su estimación determinística $157,5 (ecuación 2). Este es un resultado propio de un enfoque de opciones, que permite capturar la totalidad de escenarios contingentes proyectados. Para ilustrar el funcionamiento del modelo y las principales diferencias con los resultados que arrojan las ecuaciones 1 y 2, se sensibiliza la razón de endeudamiento y la tasa de interés. De esta forma, la tabla 8 presenta los resultados del análisis de sensibilidad correspondiente a las ecuaciones 6 y 7 (ahorro fiscal con opciones - AFO).
Tabla 8 Resultados del análisis de sensibilidad ecuaciones 6 y 7
| $ 210,65 | 20% | 30% | 45% | 50% | 70% | 100% |
|---|---|---|---|---|---|---|
| 4% | $ 54,57 | $ 81,37 | $ 122,05 | $ 135,61 | $ 163,84 | 234,057211 |
| 8% | $ 108,49 | $ 140,43 | $ 210,65 | $ 234,06 | $ 318,73 | 441,614962 |
| 12% | $ 140,43 | $ 210,65 | $ 307,35 | $ 341,50 | $ 453,93 | 377,356408 |
| 20% | $ 234,06 | $ 341,50 | $ 486,36 | $ 365,28 | $ 425,23 | 194,85528 |
Fuente: elaboración propia.
Por otra parte, la tabla 9 aplica análisis de sensibilidad, suponiendo ahorro fiscal determinístico (AFD) (ecuaciones 1 y 2). En este caso, la tasa de actualización empleada es la libre de riesgo, mientras que los intereses reconocen el costo de deuda (ki) del 8%.
Tabla 9 Resultados del análisis de sensibilidad ecuaciones 1 y 2
| $ 252,00 | 20% | 30% | 45% | 50% | 70% | 100% |
|---|---|---|---|---|---|---|
| 4% | $ 56,00 | $ 84,00 | $ 126,00 | $ 140,00 | $ 196,00 | $ 280,00 |
| 8% | $ 112,00 | $ 168,00 | $ 252,00 | $ 280,00 | $ 392,00 | $ 560,00 |
| 12% | $ 168,00 | $ 252,00 | $ 378,00 | $ 420,00 | $ 588,00 | $ 840,00 |
| 20% | $ 280,00 | $ 420,00 | $ 630,00 | $ 700,00 | $ 980,00 | $ 1.400,00 |
Fuente: elaboración propia.
A partir de lo anterior, queda manifestada la diferencia entre los enfoques, la cual reside en el carácter contingente que debe otorgársele a la valuación del ahorro fiscal. Más allá de la cuestión matemática, el enfoque de opciones arroja un valor resumen de los posibles futuros no determinísticos. Por el contrario, la concepción clásica supone determinismo en la estimación del valor del ahorro fiscal (ecuación 2); por lo tanto, la existencia de riesgo o su prescindencia dependerá de la tasa empleada (Modigliani y Miller, 1963; Miles y Ezzell, 1985; Fernández, 2014). No se debe perder de vista que, ceteris paribus, el conjunto de variables macroeconómicos que explican ahorros fiscales, se condicionan a la existencia de resultados imponibles. Dado lo anterior, la Figura 2 grafica la relación entre ahorros fiscales, calculados con ambos enfoques y la evolución del endeudamiento.

Fuente: elaboración propia.
Figura 2 Evolución del ahorro fiscal en relación al endeudamiento de la firma enfoques AFO y AFD
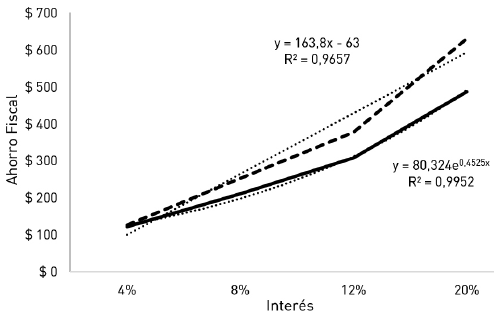
La curva exponencial es la que mejor ajusta los datos en el modelo AFO y la lineal para explicar la evolución del AFD, en relación a la deuda. Nuevamente para ambos se confirma la misma lógica, sin considerar riesgos de insolvencia, el incremento del apalancamiento financiero presenta una relación positiva con los ahorros fiscales.
En el modelo AFO la forma funcional es exponencial, producto de la asimetría positiva de las opciones reales ante variaciones positivas de variables directamente relacionadas con la prima8. En el caso de AFD, por su carácter determinístico se ajusta a relaciones lineales. Por lo tanto, la figura 3 supone fijo el nivel de endeudamiento (45% del valor del activo) y se concentra en la relación que existe entre el ahorro y la tasa de interés. Igual que en el caso anterior, la tendencia en AFO se ajusta perfectamente a un modelo exponencial y en AFD a un modelo lineal.
4.2. El modelo binomial, liquidación de la firma y ahorros fiscales
En este apartado se analiza el modelo en su totalidad, donde se proyecta el valor de la firma y el valor del escudo fiscal. La tabla 10 desarrolla la primera rejilla binomial, donde en la primera fila de cada nodo se proyecta el valor de la firma (V) según ecuación la A.1 (anexos). Los coeficientes de ascenso y descenso son los empleados en el apartado 4.1, diferenciándose por el hecho de que el valor de la firma sigue un proceso geométrico. La segunda fila de cada nodo proyecta el EBIT, bajo un proceso aritmético browniano conforme se desarrolló en la tabla 2. La tercera fila del nodo presenta el valor de la deuda según ecuación A.2 (anexos).
Tabla 10 Rejilla binomial valores proyectados V, EBIT y D.
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| $ 900,00 | $ 1.149,44 | $ 1.468,03 | $ 1.874,90 | $ 2.394,56 | $ 3.058,23 | V |
| $ 100,00 | $ 141,91 | $ 183,81 | $ 225,72 | $ 267,63 | $ 309,53 | EBIT |
| $ 36,00 | $ 36,00 | $ 36,00 | $ 36,00 | $ 36,00 | $ 486,00 | D |
| $ 570,80 | $ 729,00 | $ 931,05 | $ 1.189,10 | $ 1.518,67 | V | |
| $ 70,47 | $ 112,38 | $ 154,28 | $ 196,19 | $ 238,10 | EBIT | |
| $ 36,00 | $ 36,00 | $ 36,00 | $ 36,00 | $ 486,00 | D | |
| $ 362,01 | $ 462,35 | $ 590,49 | $ 754,15 | V | ||
| $ 40,94 | $ 82,84 | $ 124,75 | $ 166,66 | EBIT | ||
| $ - | $ 36,00 | $ 36,00 | $ 486,00 | D | ||
| $ 229,59 | $ 293,23 | $ 374,50 | V | |||
| $ 11,41 | $ 53,31 | $ 95,22 | EBIT | |||
| $ 36,00 | $ 36,00 | $ 486,00 | D | |||
| $ 145,61 | $ 185,97 | V | ||||
| -$ 18,12 | $ 23,78 | EBIT | ||||
| $ 36,00 | $ 486,00 | D | ||||
| $ 92,35 | V | |||||
| -$ 47,66 | EBIT | |||||
| $ 486,00 | D |
Fuente: elaboración propia.
En la tabla 11 son calculados los valores resultantes de aplicar las ecuaciones A.3, A.4 y A.5 (anexos), esto es el valor del capital propio (E), deuda (D) y empresa (V) no condicionado a ningún evento de liquidación.
Tabla 11 Rejilla binomial valores proyectados E, D y V no condicionados
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| $ 459,67 | $ 700,47 | $ 1.042,15 | $ 1.520,46 | $ 2.191,96 | $ 3.133,77 | E |
| $ 320,93 | $ 375,06 | $ 414,74 | $ 439,75 | $ 462,30 | $ 486,00 | D |
| $ 780,60 | $ 1.075,53 | $ 1.456,88 | $ 1.960,21 | $ 2.654,26 | $ 3.619,77 | V |
| $ 278,54 | $ 448,25 | $ 695,20 | $ 1.039,10 | $ 1.522,77 | E | |
| $ 301,87 | $ 375,03 | $ 432,47 | $ 462,30 | $ 486,00 | D | |
| $ 580,41 | $ 823,28 | $ 1.127,67 | $ 1.501,40 | $ 2.008,77 | V | |
| $ 146,36 | $ 260,18 | $ 440,37 | $ 686,81 | E | ||
| $ 262,99 | $ 358,26 | $ 447,42 | $ 486,00 | D | ||
| $ 409,34 | $ 618,44 | $ 887,79 | $ 1.172,81 | V | ||
| $ 53,67 | $ 116,30 | $ 252,00 | E | |||
| $ 199,40 | $ 309,91 | $ 455,63 | D | |||
| $ 253,07 | $ 426,21 | $ 707,63 | V | |||
| $ - | $ - | E | ||||
| $ 115,13 | $ 203,46 | D | ||||
| $ 115,13 | $ 203,46 | V | ||||
| $ - | E | |||||
| $ 43,35 | D | |||||
| $ 43,35 | V |
Fuente: elaboración propia.
La tabla 11 constituye el insumo para estimar el valor de la firma condicionado a las probabilidades de insolvencia, computando el ahorro fiscal. Con dicha información se está en condiciones de construir la tercera rejilla expuesta en la tabla 12. En efecto, primero se debe estimar el valor de la firma en el horizonte T, los pares de ecuaciones que se activan por fila son: capital propio9 (ec.8-continuidad); (ec.11-liquidación); deuda10 (ec.9-continuidad; ec.12-liquidación); empresa11 (ec.10-continuidad; ec.13-liquidación).
Tabla 12 Rejilla binomial valores proyectados E, D y V condicionados
| t=0 | 1<t<T | T | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | |
| $ 987,29 | $ 1.045,03 | $ 1.442,84 | $ 1.962,78 | $ 2.675,90 | $ 3.133,77 | E |
| $ 389,41 | $ 411,06 | $ 450,74 | $ 475,75 | $ 498,30 | $ 486,00 | D |
| $ 1.376,70 | $ 1.456,09 | $ 1.893,58 | $ 2.438,54 | $ 3.174,20 | $ 3.619,77 | V |
| $ 492,52 | $ 747,91 | $ 1.066,09 | $ 1.451,60 | $ 1.522,77 | E | |
| $ 337,87 | $ 411,03 | $ 468,47 | $ 498,30 | $ 486,00 | D | |
| $ 830,39 | $ 1.158,94 | $ 1.534,56 | $ 1.949,90 | $ 2.008,77 | V | |
| $ 317,71 | $ 499,19 | $ 781,43 | $ 686,81 | E | ||
| $ 262,99 | $ 394,26 | $ 483,42 | $ 486,00 | D | ||
| $ 580,70 | $ 893,45 | $ 1.264,85 | $ 1.172,81 | V | ||
| $ 88,56 | $ 262,50 | $ 252,00 | E | |||
| $ 89,67 | $ 152,30 | $ 455,63 | D | |||
| $ 323,96 | $ 608,42 | $ 707,63 | V | |||
| $ - | $ - | E | ||||
| $ 123,12 | $ 203,46 | D | ||||
| $ 123,66 | $ 203,46 | V | ||||
| $ - | E | |||||
| $ 43,35 | D | |||||
| $ 43,35 | V | |||||
Fuente: elaboración propia.
Los valores estimados recursivamente en el segmento intermedio 1<t<T son: capital propio12 (ec.14-continuidad; ec.17-liquidación); deuda13 (ec.15-continuidad; ec.18-liquidación); empresa14 (ec.16-continuidad; ec.19-liquidación).
Finalmente, en t=1→0, las ecuaciones 20 (capital propio), 21 (deuda) y 22 (valor de la empresa) se aplican de manera recursiva. Los valores obtenidos se presentan en la tabla 12.
Del análisis de sensibilidad y suponiendo la tasa constante (tabla 13), el tradicional modelo de Modigliani y Miller (MM)15 arroja un valor creciente a medida que aumenta el apalancamiento financiero de la firma. En cambio, el modelo binomial mantiene el valor de la firma constante, presentando una leve tendencia negativa producto del incremento de la probabilidad de insolvencia.
Tabla 13 Sensibilidad de valores modelos valoración binomial (VB) y MM en relación con el apalancamiento
| ki=8% | 20% | 30% | 45% | 50% | 100% |
| MM | $ 1.112,00 | $ 1.168,00 | $ 1.252,00 | $ 1.280,00 | $ 1.560,00 |
| VB | $ 1.380,22 | $ 1.380,22 | $ 1.376,70 | $ 1.376,70 | $ 1.370,19 |
Fuente: elaboración propia.
La figura 4 expone el comportamiento indicado, la forma funcional del valor para el modelo binomial es exponencial del tipo V l = V u e -bD . En el caso del modelo tradicional la tendencia se explica por una curva del tipo V l = V u + bD .
Los resultados obtenidos indican que el modelo binomial determina el valor de la firma en función a la evolución del EBIT y la capacidad de repago de la deuda. De esta forma, el valor estimado surge por condicionarse a probabilidades de insolvencia y consecuente liquidación. Además, ajusta el impacto positivo del valor contingente del ahorro fiscal a los potenciales escenarios, en particular de no ganancia. La tabla 14 muestra el impacto porcentual del ahorro fiscal sobre el valor de la firma, a medida que aumenta el apalancamiento.
Tabla 14 Relación ahorro fiscal-valor de la firma
| AF/V | 20% | 30% | 45% | 50% | 100% |
| MM | 11,2% | 16,8% | 25,2% | 28,0% | 56,0% |
| VB | 7,9% | 10,2% | 15,3% | 17,0% | 23,3% |
Fuente: elaboración propia.
Nuevamente, la tabla 14 confirma que el impacto del ahorro fiscal es menor en el modelo binomial, producto de la reducción de la base imponible e incremento de posibilidades de insolvencia.
5. Conclusiones
El trabajo presentó un modelo numérico experimental que otorga un tratamiento contingente al valor actual derivado de los ahorros fiscales y condiciona el valor de los activos a las posibilidades de liquidación de la empresa. La clave reside en adaptar el enfoque de opciones, en virtud a su tratamiento de los contingentes escenarios futuros de continuidad o liquidación de la firma. Los hechos futuros son producto de la evolución de los resultados operativos, condicionando el pago de la deuda y la existencia de ahorros fiscales. Por ende, es difícil o vagamente ajustado a la realidad suponer linealidad en el comportamiento del valor de la firma, como si lo hace el modelo de descuento de flujos de fondos, en sus versiones tradicionales.
Respecto de los ahorros fiscales, su valor está condicionado por variables como la magnitud y presencia de resultados imponibles, valor del impuesto a las ganancias operativo e intangibilidad de las normas tributarias. En este aspecto, el debate en materia financiera es profundo con dos posiciones extremas destacadas, como la propuesta de Modigliani y Miller (1963) o Miles y Ezzell (1980,1985) y diferentes matices que cobran las propuestas intermedias. En el presente trabajo se propone estimar el valor del ahorro fiscal como una cartera de opciones. Su valor contingente es representado por una combinación entre una posición larga y una posición corta en un call, con diferentes precios de ejercicio e igual fecha de vencimiento. El enfoque permite:
a) Asignar un tratamiento contingente a los ahorros fiscales futuros, condicionados a la existencia de escenarios que permitan la deducibilidad de intereses.
b) Evitar el debate sobre la tasa de actualización debido a que el enfoque de opciones utiliza la tasa libre de riesgo y el ajuste se practica en los flujos.
Finalmente, se ha desarrollado un modelo binomial de valoración que integra el tratamiento como canasta de opciones de los ahorros fiscales con los escenarios de continuidad y liquidación. Esto permite generar una función de valor exponencial, propio del proceso geométrico y aritmético browniano al que evoluciona el valor y los resultados operativos, como de la asimetría de los modelos de opciones. Los resultados obtenidos en el análisis de sensibilidad, evidencian el impacto atenuado del valor actual de los ahorros fiscales sobre el valor actual de la firma. Este comportamiento es el resultado de considerar los estados contingentes.
No se debe perder de vista que valuar una empresa constituye un trabajo intelectual, la complejidad de variables interrelacionadas condicionadas a futuros escenarios, se reducen a un valor esperado y dispersión relativa sobre este, para la toma de decisiones. Es por ello que el modelo utilizado debe incorporar la contingencia de los futuros que condicionan el valor de la firma.