Fecha de recepción: 9 de abril de 2010 Fecha de aprobación: 30 de mayo de 2010

RESUMEN

En este trabajo, se presenta el modelado de un Sistema de Manufactura Flexible (SMF), con procesos concurrentes y recursos compartidos mediante Sistemas a Eventos Discretos (SED), específicamente Redes de Petri (RdP), y GRAFCET. El SMF se plantea como un modelo hipotético que se modela con una RdP con el objeto de identificar su dinámica y hallar la secuencia óptima de funcionamiento del sistema. Se desarrolló un modelo matemático que permite estimar el vector de tiempo acumulado de un proceso modelado mediante una RdP, el cual constituye la base para hallar la mejor secuencia posible del sistema modelado. Por último, se realizó una implementación en el Laboratorio de Automatización de la Universidad Militar Nueva Granada, que simula el funcionamiento del SMF modelado por un montaje electrohidroneumático controlado con GRAFCET mediante PLC.

Palabras Clave: GRAFCET, sistemas a eventos discretos, sistemas de manufactura flexible, redes de Petri.

ABSTRACT

This paper shows a model of Flexible Manufacturing System (FMS) with concurrent processes and shared resources based on Discrete Event Systems through Petri Nets (PN) and GRAFCET. FMS is represented by a hypothetic model that is modeled by a PN to identify its dynamic and achieve the optimal system sequence. A mathematical model was developed to find the time accumulated vector for processes in a system modeled by PN. Using this vector it is possible locate the best system sequence. Finally, in order to simulate the FMS modeled, an electro-hydro-pneumatic assembly controlled by GRAFCET through PLC was implemented in Automation Lab at Universidad Militar Nueva Granada.

Keywords: discrete event systems, flexible manufacturing systems, GRAFCET, Petri nets.

INTRODUCCIÓN

Los Sistemas de Manufactura Flexible (SMF) pueden representarse con Sistemas Dinámicos Híbridos y modelados mediante Sistemas a Eventos Discretos con técnicas tales como Redes de Petri y GRAFCET. Los SMF constan de varias estaciones de trabajo o máquinas controladas por computadora y conectadas entre sí, por un sistema de alimentación y transporte que permite el flujo de trabajos entre los componentes del sistema global. Esta estructura permite la manufactura de múltiples productos de forma simultánea, brindando gran flexibilidad y adaptabilidad [4]. Dado que este tipo de sistemas resulta ser de mayor complejidad que los sistemas convencionales por su modelado y programación, es necesario la implementación de teorías avanzadas tales como las teorías de Sistemas a Eventos Discretos como Redes de Petri y GRAFCET [12] [13]. Así mismo, para encontrar secuencias óptimas de programación dentro de la producción, resulta apropiado utilizar métodos de optimización, métodos heurísticos o técnicas híbridas que combinan las ventajas de diferentes métodos [5].

Este artículo cuenta con cinco secciones divididas de la siguiente manera: la primera, presenta la introducción del trabajo realizado, estableciendo conceptos básicos sobre SMF; la segunda, muestra la descripción del modelo hipotético del Sistema de Manufactura Flexible, la representación del modelo en RdP del SMF y la caracterización del sistema; la tercera, plasma el modelo matemático desarrollado para estimar el vector de tiempo acumulado para procesos modelados mediante RdP; la cuarta, muestra la implementación Electro HidroNeumática controlada mediante GRAFCET que se llevó a cabo en el Laboratorio de Automatización de la Universidad Militar Nueva Granda; finalmente, y la última, presenta las conclusiones y trabajos futuros.

1. REPRESENTACIÓN DEL SISTEMA

En esta sección, se hace una breve descripción de las teorías de Sistemas a Eventos Discretos (SED), Redes de Petri (RdP), y GRAFCET, ya que todo el trabajo presentado se basa en las teorías mencionadas. Posteriormente, se describe el sistema desarrollado que se basa en un modelo hipotético de producción de chocolates, que se escogió por que tiene dos procesos concurrentes y tres recursos compartidos. Por último, se presenta la RdP diseñada para este sistema con su caracterización respectiva.

1.1. DESCRIPCIÓN TEÓRICA DE SOPORTE

Los Sistemas a Eventos Discretos (SED), permiten modelar Sistemas Dinámicos Híbridos (SDH). Los SDH combinan sinérgicamente, la lógica y la dinámica continua de sistemas; un clásico ejemplo, es el caso de procesos de tiempo continuo que se supervisan utilizando algoritmos de lógica de marcado y decisión [1], [2]. Los SED permiten representar sistemas en los cuales el comportamiento de entrada y salida se encuentra descrito en secuencias a eventos, sujetos al estado que tenga un número finito de cambios dentro de un intervalo finito de tiempo [3]. Los SED reemplazan la discretización por la cuantificación de las variables de estado, mejorando la respuesta dinámica de los sistemas de control digital y reduciendo el costo computacional y el tráfico de información entre la planta y el controlador. Dentro de las técnicas de SED, se contemplan las Redes de Petri y el GRAFCET.

Las Redes de Petri (RdP), fueron desarrolladas como una herramienta para simular propiedades dinámicas de los sistemas complejos mediante modelos gráficos de procesos concurrentes y distribuidos [6]. Una RdP es un método de modelización de Sistemas a Eventos Discretos con el cual es posible controlar, evaluar y optimizar diferentes procesos. Las RdP son grafos orientados compuestos por lugares y transiciones que se encuentran unidos por arcos, donde los lugares representan los estados del modelo, los arcos indican la dirección de evolución de la RdP y las transiciones representan las entradas del sistema; de su activación o desactivación dependerá el funcionamiento de la red [8] [9].

La sigla GRAFCET significa GRÁfico Funcional de Control de Etapas y Transiciones [10]. GRAFCET es un método gráfico de modelación y diseño de automatismos que se fundamenta en la teoría de Redes de Petri. Dentro de las ventajas que introduce este método, están la metodología y la estructura que lo representa, ya que con esto es posible obtener gran claridad, legibilidad y síntesis a la hora de controlar procesos o sistemas a eventos discretos. Un GRAFCET se comporta como una red de Petri viva, binaria y por ende, conforme [7]; por tal motivo, los elementos que componen el GRAFCET se aproximan en gran medida a los de una RdP [11].

1.2. DESCRIPCIÓN DEL SISTEMA

El modelo hipotético está enmarcado en una planta de producción de chocolates en donde se tienen dos procesos de producción paralelos: barras y bolas de chocolate. Cada uno de estos procesos está compuesto por dos acciones u operaciones: 1) el llenado del chocolate en el molde y 2) el transporte de los chocolates para su posterior empaque. Con el fin llevar a cabo las acciones definidas, se cuenta con tres máquinas, específicamente manipuladores industriales, que son compartidas por ambos procesos. Las funciones de cada manipulador son las siguientes: 1) hace el llenado para los dos procesos; 2) efectúa la acción de transporte para ambos procesos; y 3) realiza el llenado para el proceso 2 y el transporte para el proceso 1. Las figuras 1 y 2 muestran la descripción de los procesos mencionados.

1.3. RED DE PETRI (RDP) DEL SMF

La RdP del modelo hipotético consta de los dos procesos de producción paralelos. El Proceso 1 (bolas de chocolate), se encuentra en el lado derecho de la RdP, con un ligero sombreado, mientras que el Proceso 2 (barras de chocolate), se encuentra en el lado izquierdo de la RdP. Los lugares o plazas que representan las máquinas que intervienen en el proceso, están encerrados en un rectángulo y tienen la marca M1, M2 y M3 respectivamente. Para el análisis de la red, las máquinas se llamarán "Recursos Compartidos".

Mediante una RdP se modela el sistema hipotético planteado que se muestra en la figura 3; la descripción de cada lugar de la red, se presenta en las tablas 1, 2 y 3.

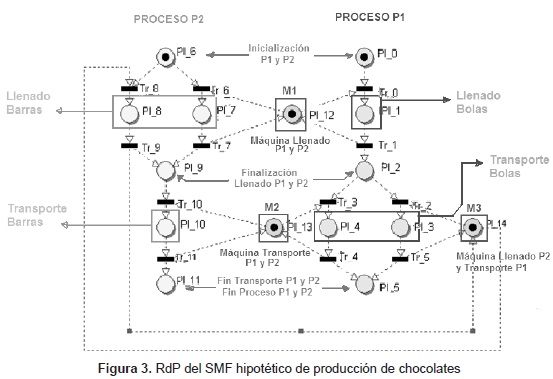
Los lugares de operación de la RdP modelan las actividades que se deben realizar en cada proceso. A cada operación (actividad), se le asigna un tiempo específico de acuerdo con la máquina utilizada; estos tiempos se reflejan en la tabla 4. Los tiempos están especificados en Unidades de Tiempo (UT).

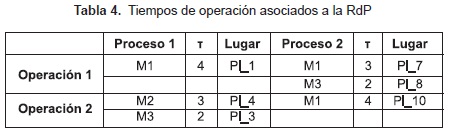
A modo de ejemplo, se analizará la operación 1 del proceso P2 que hace alusión al llenado de las barras de chocolate: Si se realiza la operación con la máquina M1 (Pl_1), tardará 3 UT, mientras que la misma operación con la máquina M3 (Pl_1), durará 2 UT. Analizando la RdP modelada y la caracterización de la misma, se establecieron las siguientes secuencias de funcionamiento del sistema, que son las posibles alternativas significativas que puede tomar la RdP de la figura 3.

• secuencia 1 (Sd1) -> P1: Pl_1, Pl_3 y P2: Pl_7, Pl_10
• Secuencia 2 (SD2) -> P1: Pl_1, Pl_4 y P2: Pl_7, Pl_10
• secuencia 3 (Sd3) -> P1: Pl_1, Pl_4 y P2: Pl_8, Pl_10
• Secuencia 4 (SD4) -> P1: Pl_1, Pl_3 y P2: Pl_8, Pl_10

2. MODELO MATEMÁTICO

Basados en el modelo matemático de la Ecuación de Tiempo Remanente (ETR), elaborado por Mejía [5], [14], [15], se desarrolla la Ecuación de Tiempo Acumulado de Procesos (ETAP), representada por la Expresión 1.

Donde M(k + 1) es el vector de marcado que indica el estado de evolución de la red (Expresión 2) y M_T(k + 1), es el vector de tiempo acumulado del proceso, que almacena la información de tiempo para cada operación, según la evolución de la red (Expresión 3).

A es la matriz de incidencia del sistema modelado. M(k) representa el vector de marcado en el instante k, es decir, en el instante anterior. El vector M_T(k), representa el tiempo de proceso acumulado para el instante k.

T simboliza la matriz diagonal de tiempos de proceso para los lugares de operación, de dimensiones [nxn], y matemáticamente se evalúa como el conjunto expuesto en la Expresión 4.

Donde t_ij = t_i, cuando i = j y cuando t_ij sea un lugar de operación, t_ij = 0 en cualquier otro caso.

t_i es la i-ésima posición del vector de tiempo de espera (time delay), asociado con los lugares de operación o visto desde otra perspectiva, se dice que t_i es el tiempo que tarda en llevarse a cabo la operación asociada al lugar ⁱ, dentro de un proceso simulado mediante una rdP.

u(k) es el vector de control de dimensiones [mx1], determina qué transición se dispara después de k disparos, u_j(k) es la j-ésima posición de u en el tiempo k.

La ETAP calcula de forma acumulada en cada instante de evolución de la red el tiempo que gasta un proceso de producción con procesos concurrentes y recursos compartidos. La diferencia fundamental con la ETR es que se necesita conocer el tiempo final de cada posible secuencia de operación, mientras que la ETAP lo va calculando según sea la evolución de la red. Es importante tener en cuenta que el modelo matemático de la ETAP está planteado para condiciones ideales, es decir, que no tiene en cuenta los tiempos de espera entre operaciones.

Los valores para las variables de la ETAP para el modelo hipotético modelado de producción de chocolates, se presentan en las siguientes expresiones:

Matriz de incidencia de la red:

Matriz de tiempos de operación:

El vector de marcado inicial

Vectores de control o secuencias de disparo

Evaluando la ETAP con el vector de control u₄(k), junto con los demás parámetros de la ecuación, se obtuvo el resultado enunciado en la expresión 13.

Es importante que el lector tenga en cuenta que las ecuaciones de tiempo relacionadas en este documento, representan los casos ideales dentro de los cuales no existen tiempos de espera entre procesos.

3. IMPLEMENTACIÓN

El sistema hipotético se llevó a simulación física, mediante un montaje electrohidroneumático en el cual se simula la RdP de la figura 3, con los elementos que se encuentran en el Laboratorio de Automatización de la Universidad Militar Nueva Granada, tal como se aprecia en la figura 4. Dentro de este ensamble, el montaje neumático representa los procesos o secuencias de actividades del sistema global y el montaje hidráulico representa las máquinas o recursos compartidos del sistema.

En el montaje neumático, se utilizaron tres cilindros de doble efecto para las operaciones de llenado y tres cilindros de simple efecto para las operaciones de transporte. Se usaron dos sensores ópticos, uno inductivo y tres finales de carrera para las señales de los cilindros de doble efecto.

El montaje hidráulico está compuesto por tres motores que simulan las tres máquinas o recursos compartidos, y tres válvulas que permiten el control de los motores, dos de ellas biestables de tres posiciones y una monoestable de dos posiciones. Cada vez que se accione un motor, significará que una máquina está siendo utilizada dentro del sistema modelado: el movimiento del motor en un sentido simulará que está siendo utilizada por un proceso; si gira en sentido contrario significará que está siendo utilizada por el otro proceso; y cuando el motor esté estático significará que el recurso no está siendo utilizado por alguno de los procesos.

Además de los motores, para el funcionamiento de las máquinas, se programaron luces industriales que permiten visualizar en tres colores diferentes el funcionamiento de las mismas.

Las tablas 5 a 7 muestran la descripción de los elementos del montaje electrohidroneumático. La tabla 5 contiene el listado de convenciones utilizadas para definir los elementos de la implementación; la tabla 6 presenta la relación de entradas del sistema, y la tabla 7 muestra la relación de los elementos de salida del sistema.

El modelo de la RdP se lleva a implementación en un autómata (PLC), que controla el sistema mediante la técnica de GRAFCET [11]. Se utilizó el PLC 300 de Siemens bajo el software Simatic - S7 Graph [14]. La estructura de los GRACET programados se puede ver en la figura 5.

Para el modelo hipotético implementado, se consideraron cuatro secuencias de funcionamiento del sistema, que fueron expuestas en la Sección II - Ítem C. A cada secuencia se le aplicó la ETAP, y se probaron sus resultados en la implementación electro hidroneumática controlada por GRAFCET.

A continuación, se presenta un análisis de las cuatro posibles secuencias de producción del sistema:

En la primera (SD1), que se muestra en la figura 6, puede observarse cómo el llenado, para las barras y para las bolas, se lleva a cabo mediante la misma máquina M1, desaprovechando el recurso M3; para este caso, una de las operaciones deberá esperar a que la otra concluya. En la fase de transporte, se optimizan los recursos debido a que siempre se está efectuado con máquinas diferentes para cada proceso; sin embargo, debido a la condición anterior, bastaría con una sola máquina ya que no sería posible tener barras y bolas a la vez.

En la segunda (SD2), la operación de llenado para las barras y las bolas se realiza con la máquina M1 y la operación de transporte se lleva a cabo con la máquina M2. Analizando la estructura de la red y el comportamiento de la misma, se puede llegar a la conclusión de que la secuencia SD2 es la menos apropiada para mejorar los tiempos de producción del sistema, debido a que tanto para P1 como P2 los recursos se comparten en todas las operaciones efectuadas, inutilizando los recursos de la máquina de M3.

Para la tercera (SD3), el llenado de las barras se realiza con la máquina M3 y el de bolas con la máquina M1, con lo cual se maximiza la operación de llenado de los productos; sin embargo, en la etapa de transporte se comparten el recurso M2 para P1 y para P2.

Para la secuencia SD4, cada operación dentro de cada proceso, utiliza un recurso diferente, lo cual hace que el proceso se efectúe en menor tiempo, maximizando el funcionamiento de los recursos (máquinas).

Al evaluar la ETAP, la secuencia que ocupa menor tiempo de producción es la SD4, con un valor total de 6 UT para cada uno de los procesos; estos resultados pueden apreciarse en la Expresión 12, donde se evalúa la ETAP para la SD4. Los tiempos de espera del sistema para la SD4 son de 6 UT para P1 y de 8 UT para P2 (figura 7).

La tabla 8 muestra la relación de tiempos para cada secuencia presentada. Tomando estos resultados de tiempo y teniendo en cuenta el análisis realizado para cada secuencia, se puede concluir que la secuencia SD4 es la mejor secuencia de funcionamiento para el sistema, debido a que maximiza los recursos de máquina y minimiza el tiempo de producción.

4. CONCLUSIONES

De acuerdo con la teoría aplicada y a los resultados obtenidos a nivel físico y nivel de simulación, se seleccionó la secuencia SD4 como la mejor secuencia para el sistema hipotético implementado basado en el criterio de tiempo mínimo de producción.

Se planteó un modelo matemático que calcula el tiempo de operaciones en procesos concurrentes con recursos compartidos, cuyo objetivo es encontrar medidas de desempeño del sistema que permitan determinar la secuencia que mejore los tiempos de producción del sistema modelado.

Como trabajo futuro, se plantean dos tareas específicas: 1) Perfeccionar el modelo matemático de la ETAP con el fin de tener en cuenta todos los tiempos de las posibles secuencias de producción; y 2) mediante técnicas de optimización o técnicas heurísticas, pueda encontrase la secuencia óptima de producción para un proceso industrial, sin tener en cuenta el número de estados u operaciones que este pueda llegar a tener.

REFERENCIAS BIBLIOGRÁFICAS

[1] A van der Schaft and H. Schumacher (2000). An introduction to hybrid dynamical systems. Springer, Berlin.         [ Links ]

[2] Zaytoon J. (2001). Systèmes dynamiques hybrides. Hermès Science Publication, Paris.         [ Links ]

[3] Kofman Ernesto. (2003) Simulación y Control de Sistemas Continuos por Eventos Discretos; Rosario, Argentina. Tesis Doctoral (Doctor en Ingeniería). Universidad Nacional del Rosario. Facultad de Ciencias Exactas, Ingeniería y Agrimensura.         [ Links ]

[4] Vallejo E. (1998). Sistemas Flexibles de Manufactura. Ingeniería & desarrollo. Universidad del Norte. 3-4: 43-49. Barranquilla - Colombia.         [ Links ]

[5] Castro López A. L. y Mejia G. (2005). Combinación de Métodos Heurísticos con Redes de Petri para la Programación de Sistemas de Manufactura Flexible. Departamento de Ingeniería Industrial. Universidad de los Andes. Bogotá - Colombia.         [ Links ]

[6] Peña P. Alirio J. (1999) Sobre las Redes de Petri R-difusas. On R-fuzzy Petri Nets. Divulgaciones Matemáticas Vol. 7. No.1, pp. 87-99. Laboratorio de Algebra teórica y computacional (LATyC). Facultad de Ciencias, Universidad de Zulia, Venezuela.         [ Links ]

[7] Simarro R. (2007). Apuntes de clase Automatización Industrial. Universidad Politécnica de Valencia. personales.upv.es/rausifer/        [ Links ]

[8] Petri Nets (2000). 21^st International Conference on Applications and Theory of Petri Nets. Aarhus, Denmark.         [ Links ]

[9] Tadao Murata (1989). Petri Nets: Properties, Analysis and Applications. Proceedings of the IEEE, Vol. 77, No. 4.         [ Links ]

[10] Balcells. J., Romeral J.L. (1998) Autómatas Programables. Ed. Alfaomga marcombo ISBN 970-15-0247-7.         [ Links ]

[11] González V. (2005). Memorias Curso sobre GRAFCET y GEMMA. Informática Industrial II - Universidad de Oviedo. Oviedo - España. http://www.isa.uniovi.es/~vsuarez//ii2/index.htm.         [ Links ]

[12] Mu Der Jeng, Reyu Wen Jaw, Pen Li Hung (1997). Scheduling FMS with Due Dates Based on Petri State Equations. Proceedings of the IEEE. p 2724.         [ Links ]

[13] H. Yu, A. Reyes, S. Cang and S. Lloyd (2003). Combined Petri net modeling and AI based heuristic hybrid search for flexible manufacturing systems. Part 1 Petri net modeling and heuristic search. Computers & Industrial Engineering.         [ Links ]

[14] S7 Graph Siemens. (2008) http://www.automation.siemens.com/simatic/industriesoftware/html_76/products/simatic-s7-graph-maintenance.htm.         [ Links ]

[15] Mejia Gonzalo and Odrey Nicholas G. Petri Net Models and Heuristic Search for scheduling of Manufacturing Systems: A comparative Study. Departamento de Ingeniería Industrial. Universidad de los Andes. Bogotá - Colombia. Departamento de Ingeniería Industrial y de Sistemas. Universidad de Lehigh. Bethlehem, PA, USA.         [ Links ]

[16] Mejia Gonzalo (2003). Timed Petri net modeling and optimization with heuristic search for flexible manufacturing workstations. Emerging Technologies and Factory Automation, IEEE Conference Proceedings. ETFA apos;03. Volume 1, Issue. Page(s): 211 - 217 vol.1 DOI 10.1109/ ETFA.2003.1247708.         [ Links ]