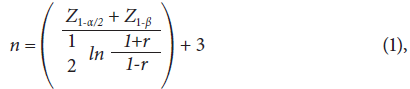Introducción
Una estructura de pavimento está conformada por capas de diferente espesor y calidad, que se apoyan sobre una capa de soporte conocida como subrasante. Convencionalmente, las capas que forman la estructura del pavimento son sub-base, base y carpeta asfáltica para pavimentos flexibles, y subbase y losa de concreto hidráulico para pavimentos rígidos. En algunos casos, y principalmente en vías de primer nivel en pavimentos flexibles, se han incorporado capas adicionales usualmente estabilizadas o se estabilizan las capas granulares de tal manera que se aprovechen mejor las propiedades de cada componente de la estructura y se reduzca el espesor de las capas del pavimento [1]. En cualquiera de los casos, el tipo y las propiedades de la subrasante son determinantes en los requerimientos y en el futuro desempeño de la estructura de pavimento. La subrasante puede estar constituida por el suelo en su estado natural o por suelo mejorado mediante geosintéticos, procesos mecánicos o químicos [2]. Para las subrasantes de suelos finos, como las estudiadas en este artículo, las investigaciones recientes han demostrado que la subrasante controla en general (alrededor del 80%) las deformaciones de la estructura de pavimento [3].
El nivel de esfuerzos en pavimentos rígidos o flexibles correctamente diseñados es considerablemente bajo comparado con la resistencia de los materiales, por lo que no se espera falla por esfuerzo cortante de las capas para las cargas de diseño. Las deformaciones del pavimento bajo los esfuerzos ocasionados por las repeticiones de cargas del tráfico son las que definen el deterioro y la funcionalidad de la estructura. Por tal razón, la rigidez elástica es la propiedad más importante para la caracterización de los materiales de las capas del pavimento, incluida la subrasante. El ensayo de módulo resiliente (MR), que mide la relación entre la amplitud de un esfuerzo desviador cíclico y la deformación recuperable, es una prueba de laboratorio incorporada por algunos métodos de diseño para considerar la rigidez elástica de los materiales. No obstante, el ensayo MR requiere usar equipos especializados y personal capacitado para realizar dicho ensayo, y hay aún un gran debate sobre la variabilidad de los resultados para muestras probadas bajo condiciones similares. Por ejemplo, [4] en 2012 compararon valores de MR cuando las deflexiones se miden mediante transductores de desplazamiento internos o externos, y encontraron que las diferencias pueden ser del orden del 50%, con valores mayores de desplazamiento obtenidos mediante transductores internos. Para una misma muestra, también se observan importantes variaciones (del 50% o mayores) en los resultados de CBR (15 en total por cada ensayo) cuando se cambia el esfuerzo de confinamiento o el esfuerzo desviador [5]. Por esta razón, algunos autores han sugerido métodos simplificados para obtener un valor de diseño promedio (e. g., [6]), lo que es aún objeto de debate. Otros investigadores han sugerido predecir un único valor del módulo resiliente a partir de las propiedades índice o la resistencia al esfuerzo cortante del suelo [7].
Debido a lo anterior, varias metodologías de diseño aceptan obtener la rigidez del suelo a partir de correlaciones con otras propiedades. Por ejemplo, la AASHTO guide for design of pavement structures [8], propuesta en 1993 por la American Association of State Highway and Transportation Officials (AASHTO), acepta obtener el módulo elástico de la subrasante a partir de correlaciones con propiedades como contenido de finos, contenido de humedad, índice de plasticidad, límite líquido, entre otras. También existen diferentes procedimientos, tanto estáticos como dinámicos, que miden la resistencia o rigidez del suelo, a partir de los que se puede obtener un valor estimado del módulo resiliente. Algunos métodos estáticos incluyen: a) valor de soporte de California (CBR, por sus siglas en inglés), b) valor de resistencia Hveem (valor R) y c) ensayo de placa de carga (valor K). Entre los métodos dinámicos se encuentran a) penetrómetro dinámico de cono (DCP, por sus siglas en inglés), b) deflectómetro de impacto ligero (LWD, por sus siglas en inglés) y c) deflectómetro de impacto portátil (FWD, por sus siglas en inglés). Los ensayos descritos se realizan in situ, con excepción del CBR que puede llevarse a cabo tanto en campo como en laboratorio. Algunas de estas pruebas, i. e., FWD, se realizan sobre la superficie del pavimento y sirven para determinar tanto la rigidez de las capas de la estructura del pavimento como la de la subrasante [9-10]. [8] también permite diseñar la estructura a partir del CBR, cuya realización es más fácil, rápida y económica, comparada con el ensayo del módulo resiliente, y que ha sido usado con éxito en diseño de pavimentos durante casi un siglo. Por esta razón, la mayoría de los ensayos de campo descritos también han sido correlacionados con el CBR.
Con el fin de basar el diseño de la estructura de pavimento en su desempeño a largo plazo, e incluir variables de tipo climático y ambiental en el diseño, la AASHTO propuso en 2008 la Mechanistic-empirical pavement design guide: a manual of practice [11] para reemplazar la guía previa de 1993 [8]. La nueva metodología ha sido adoptada por algunos departamentos de transporte en los Estados Unidos desde hace menos de una década, y en América Latina y en nuestro país solo se usa para chequear diseños realizados mediante otras normativas en algunos proyectos de gran envergadura. Aunque esta nueva metodología se basa en el valor del MR para caracterizar la rigidez de la subrasante, únicamente requiere la realización directa de estos ensayos para vías de primer nivel. Para pavimentos en vías de menor importancia, el valor MR puede ser obtenido a partir de correlaciones, e. g., con el CBR o la compresión inconfinada.
Por las razones discutidas, ha sido una práctica común en países en desarrollo, e incluso en países desarrollados en vías de segundo o tercer nivel, diseñar la estructura de pavimento a partir del CBR. En los Estados Unidos, por ejemplo, el Asphalt Institute, el U.S. Army Corps of Engineers, la AASH-TO [8], incluso la Mechanistic-empirical pavement design guide: a manual of practice [11] bajo ciertas circunstancias, permiten diseñar la estructura de pavimento a partir del CBR [12]. Aunque el CBR no define una propiedad elástica del suelo, como sí lo hace el módulo resiliente, los buenos resultados obtenidos a través de su amplio uso en diseño de pavimentos [13-15], y el gran debate que aún genera el ensayo del módulo resiliente, mantiene el CBR como una de las pruebas preferidas para el diseño de pavimentos.
A pesar de su amplia aceptación y utilización, no es siempre posible realizar ensayos de CBR, en especial en suelos finos, como los discutidos en este artículo. Para subrasantes naturales de suelos finos, el CBR debería realizarse in situ o en laboratorio sobre muestras inalteradas, debido a que la recompactación de muestras en el laboratorio altera sus propiedades. El ensayo in situ, aunque es preferido porque se evalúa el suelo sin alterar su estructura o esfuerzos de confinamiento, es costoso y requiere el uso de vehículos pesados como sistema de reacción. Para estos ensayos, la subrasante debe estar nivelada y expuesta, lo que no siempre es posible, en especial en proyectos nuevos. En cuanto a ensayos de laboratorio sobre muestras inalteradas, la toma de dichas muestras no es posible en todos los casos. Por ejemplo, en proyectos nuevos en los que debido a la topografía la cota de diseño de la subrasante se localiza varios metros por debajo de la cota del terreno en el momento de la exploración (e. g., vías temporales para proyectos hidroeléctricos, de explotación minera, entre otros; o vías nuevas en zonas de topografía escarpada), la obtención de una muestra inalterada para CBR es un proceso complejo, dispendioso y en muchos casos imposible de realizar, debido a la profundidad por la que está limitada la ejecución de un apique (menor de 2 m o 3 m). Para vías existentes, no se permite realizar apiques en gran cantidad, debido a que es necesario romper el pavimento. Además, en los casos en los que se pueden tomar las muestras inalteradas, la necesidad de evaluar la condición saturada en suelos finos incrementa considerablemente el tiempo y costo de los ensayos CBR.
Cuando se realizan estudios para diseño de pavimentos, se deben ejecutar perforaciones mecánicas o barrenos manuales, usualmente en mayor cantidad y hasta profundidades mayores de las de los apiques para muestras de CBR. De esta manera, si se establece una correlación entre el valor del CBR de un suelo fino con ensayos de rutina como la compresión inconfinada o algunas propiedades índice, que se pueden realizar sobre muestras extraídas de perforaciones o barrenos, se podría realizar una mejor caracterización de la rigidez del corredor de diseño. Estos resultados podrían ser utilizados para obtener valores tentativos de CBR en aquellos sitios donde no es posible realizar estos ensayos o para ampliar la información en los tramos donde sí se han realizado estas pruebas. Debe resaltarse que la obtención del CBR a partir de estas correlaciones podría usarse para diseños preliminares, y no exime al diseñador de hacer ensayos de CBR o módulo resiliente, al menos para verificar los diseños durante la construcción.
A pesar de que existe en la literatura un número importante de correlaciones para obtener el CBR en función de las propiedades índice del suelo (e. g., [16,17]), ese no es el caso de la resistencia al esfuerzo cortante de muestras inalteradas de suelos finos, mediante el ensayo de compresión inconfinada. La poca información en la literatura corresponde a ensayos triaxiales no consolidados no drenados (UU) sobre muestras mezcladas con granulares o a ensayos sobre suelos finos con penetrómetro de bolsillo [12,18-20]. Por otra parte, las correlaciones encontradas [12,16-20] son presentadas sin realizar un previo análisis estadístico y en algunos casos se reportan pocos ensayos con gran variabilidad en los resultados.
Para ayudar a llenar ese vacío en el estado actual en ingeniería de pavimentos, este artículo presenta resultados de una investigación realizada con el fin de correlacionar el CBR inalterado con la resistencia a la compresión inconfinada del suelo y algunas propiedades índice tanto para muestras con humedad natural como saturadas. Se discuten los resultados de ensayos de CBR, clasificación y compresión inconfinada sobre 38 muestras, que cubrieron un amplio rango de propiedades de resistencia y plasticidad. Mediante gráficas de dispersión y la utilización del paquete estadístico Minitab [21], se realizan los diferentes análisis para definir cuáles de estas propiedades pueden correlacionarse con el CBR.
Materiales y métodos
Cantidad, localización y toma de muestras
En la mayoría de los casos, el número de ensayos en investigaciones experimentales en ingeniería geotécnica es limitado por factores económicos o de infraestructura y montaje, y no por la cantidad necesaria para tener un muestreo estadístico adecuado. En nuestra investigación, hallamos el número mínimo de ensayos (n) requerido desde el punto de vista estadístico, por medio del coeficiente de correlación de Pearson (r), como se indica en la ecuación (1).
donde Z 1-α/2 , Z 1-β son factores que dependen de la seguridad y el poder estadístico deseados.
Se utilizó un coeficiente de correlación de Pearson r igual a 0,60 (i. e., se espera al menos una correlación de 0,60), y una seguridad y poder estadístico del 95%. Para estas condiciones, los valores de Z 1-α/2 , Z 1-β son 1,96 y 1,645, respectivamente, y el número mínimo requerido de muestras es de 30 (ecuación (1)). Se asumió un bajo coeficiente r, debido a que este es inversamente proporcional al número requerido de muestras, i. e., si se obtiene una correlación mayor, como se espera en este estudio, se necesitaría menor número de muestras para tener un análisis estadístico confiable.
Con el fin de estudiar suelos de diferentes características, las muestras fueron extraídas de tres regiones en Colombia: a) Santiago de Cali y algunos municipios aledaños: Yumbo, Palmira, Candelaria, Florida, Jamundí; b) municipios del norte del Cauca: Puerto Tejada, Villa Rica, Miranda y Santander de Quilichao; y c) Popayán. Se eligió Popayán, debido a que ahí se encuentran suelos blandos con alto grado de humedad, provenientes de cenizas volcánicas, que difieren de las otras dos regiones.
Los ensayos de CBR y compresión inconfinada fueron realizados sobre muestras de suelo fino inalteradas; posteriormente, sobre las mismas muestras, se llevaron a cabo los ensayos de análisis granulométrico y contenido de humedad. Los límites de Atterberg se ejecutaron sobre muestras alteradas. Las muestras en campo se obtuvieron mediante apiques de aproximadamente 1,0 m x 1,0 m de sección transversal y profundidad entre 0,40 m y 1,10 m. En los apiques, se hincó el molde para los ensayos de CBR y contiguo a este se hincó el tubo de pared delgada (shelby). Las muestras inalteradas se protegieron con parafina para evitar pérdida de humedad y se llevaron al laboratorio a fin de realizar los ensayos mencionados. Las muestras alteradas fueron tomadas después de retirar el molde CBR y el tubo shelby.
Ensayos de laboratorio
Los ensayos se realizaron siguiendo las normas técnicas ASTM International. Para los 38 sitios evaluados, se ejecutaron ensayos de CBR, compresión inconfinada, límites de Atterberg, análisis granulométrico por tamizado y contenido de humedad natural, según las normas ASTM D1883-05, D2166-00, D4318-10, D6913-09 y D2216-10, respectivamente [22-26].
Los ensayos de compresión inconfinada se realizaron sobre muestras inalteradas con 5,1 cm de diámetro y una altura igual a dos veces su diámetro. Esta relación de esbeltez es sugerida por las normas técnicas para evitar el pandeo y el cruce de los planos de falla de la muestra durante la prueba. Los ensayos de CBR se realizaron para el molde estándar de 15,2 cm de diámetro y 17,8 cm de altura.
Se determinó el CBR con la humedad natural del suelo en una de las caras, posteriormente las muestras se sumergieron en agua durante cuatro días y se realizó nuevamente el ensayo sobre la otra cara, con el fin de simular las condiciones más críticas que se puedan presentar durante periodos de lluvia o para subrasantes cercanas a fuentes de agua. La tabla 1 incluye un resumen de la localización de las muestras y de los resultados de los ensayos.
Tabla 1 Ubicación de muestras y resultados de ensayos de laboratorio
| N.º | Lugar | CBR nat. (%) | CBR sat. (%) | LL (%) | PI (%) | qu (kg/cm2) | SUCS |
|---|---|---|---|---|---|---|---|
| 1 | Yumbo | 1,5 | 1,1 | 73,0 | 42,1 | 0,29 | CH |
| 2 | Candelaria 1 | 3,8 | 1,3 | 45,8 | 30,4 | 0,37 | ML |
| 3 | Candelaria 2 | 4,0 | 1,4 | 28,1 | 3,9 | 0,59 | ML |
| 4 | Popayán 1 | 14,8 | 13,7 | 80,0 | 28,1 | 3,78 | MH |
| 5 | Popayán 2 | 17,5 | 14,8 | 57,6 | 8,5 | 4,32 | MH |
| 6 | Candelaria 3 | 7,2 | 1,7 | 71,7 | 41,6 | 2,27 | CH |
| 7 | Candelaria 4 | 6,3 | 2,7 | 37,5 | 6,5 | 1,58 | ML |
| 8 | Popayán 3 | 12,2 | 3,7 | 36,0 | 10,4 | 3,00 | ML |
| 9 | Popayán 4 | 6,0 | 3,7 | 48,8 | 21,7 | 1,79 | CL |
| 10 | Popayán 5 | 6,9 | 3,6 | 56,4 | 36,9 | 2,19 | CH |
| 11 | Miranda 1 | 8,5 | 2,2 | 50,6 | 18,4 | 2,06 | MH |
| 12 | Miranda 2 | 4,3 | 3,9 | 46,7 | 16,8 | 1,20 | ML |
| 13 | Florida 1 | 3,5 | 3,1 | 40,8 | 13,0 | 1,20 | ML |
| 14 | Florida 2 | 4,2 | 3,6 | 60,6 | 24,3 | 1,72 | MH |
| 15 | Puerto Tejada 1 | 6,3 | 3,5 | 26,2 | 7,9 | 2,04 | CL |
| 16 | Puerto Tejada 2 | 5,9 | 4,4 | 81,0 | 56,6 | 1,90 | CH |
| 17 | Puerto Tejada 3 | 9,1 | 5,3 | 56,0 | 21,1 | 2,51 | MH |
| 18 | Palmira 1 | 4,3 | 2,4 | 67,1 | 27,4 | 2,17 | MH |
| 19 | Palmira 2 | 4,2 | 1,1 | 46,5 | 17,2 | 1,45 | ML |
| 20 | Palmira 3 | 3,7 | 3,3 | 44,2 | 19,2 | 1,39 | CL |
| 21 | Palmira 4 | 8,0 | 7,3 | 39,3 | 21,0 | 2,26 | CL |
| 22 | Cali 1 | 3,0 | 2,8 | 76,1 | 37,0 | 0,82 | MH |
| 23 | Cali 2 | 2,0 | 1,6 | 41,6 | 18,6 | 0,64 | CL |
| 24 | Jamundí 1 | 7,0 | 4,5 | 53,8 | 21,5 | 1,50 | MH |
| 25 | Jamundí 2 | 3,4 | 1,5 | 65,5 | 38,0 | 1,07 | CH |
| 26 | Villa Rica 1 | 9,9 | 5,3 | 54,2 | 21,4 | 2,12 | MH |
| 27 | Villa Rica 2 | 3,4 | 1,1 | 93,0 | 56,2 | 0,85 | MH |
| 28 | Villa Rica 3 | 1,3 | 0,97 | 65,7 | 29,4 | 0,21 | MH |
| 29 | Santander de Quilichao 1 | 2,0 | 1,6 | 51,1 | 17,6 | 0,67 | MH |
| 30 | Santander de Quilichao 2 | 6,9 | 3,9 | 63,9 | 16,8 | 2,59 | MH |
| 31 | Santander de Quilichao 3 | 20,0 | 12,7 | 74,3 | 36,1 | 6,63 | MH |
| 32 | Cali 3 | 5,7 | 3,3 | 58,0 | 20,5 | 2,20 | MH |
| 33 | Cali 4 | 0,93 | 0,89 | 63,0 | 26,8 | 0,10 | CH |
| 34 | Cali 5 | 14,3 | 8,3 | 45,0 | 18,2 | 3,30 | ML |
| 35 | Popayán 6 | 4,9 | 2,5 | 69,0 | 32,4 | 2,92 | MH |
| 36 | Popayán 7 | 1,6 | 0,73 | 48,1 | 14,2 | 0,68 | ML |
| 37 | Popayán 8 | 0,93 | 0,73 | 51,1 | 18,3 | 0,52 | MH |
| 38 | Popayán 9 | 2,40 | 1,8 | 53,7 | 19,0 | 1,11 | MH |
SUCS: Sistema Unificado de Clasificación de Suelos [28].
Fuente: Elaboración propia.
Resultados y análisis estadístico
Con la información obtenida de los ensayos de laboratorio se prepararon gráficas de dispersión entre el CBR, tanto natural como saturado, y las demás propiedades evaluadas. Para las variables que en las gráficas de dispersión mostraron cierta tendencia con el CBR, se realizó un análisis estadístico más detallado con diferentes modelos de regresión, con el fin de encontrar la mejor correlación entre las variables. Para verificar si un modelo de regresión simple es adecuado, se debe comprobar el cumplimiento de los siguientes supuestos: distribución normal de residuos, inexistencia de datos asimétricos o con valores atípicos y varianza constante para los residuos. Para tal fin se realizan gráficas de probabilidad normal de residuos, histograma de residuos y dispersión de residuos versus ajustes [27].
Para verificar la distribución normal de los residuos, se compara el valor P de la gráfica de probabilidad normal de residuos con un nivel de significancia especificado, a (usualmente 0,1, 0,05, 0,01), que define la probabilidad de rechazar la hipótesis nula cuando esta es cierta. Para fines prácticos en análisis estadístico, suele tomarse un nivel de significancia a = 0,05, i. e., el 5% de probabilidad de error. Más información sobre el valor a y su selección puede encontrarse en [21,29]. Si el valor de P, que mide la fuerza de la evidencia para descartar la hipótesis nula, es igual o menor que el valor de significancia, se rechaza la hipótesis nula y se concluye que los datos no siguen una distribución normal. Si, por el contrario, el valor de P es mayor que el nivel de significancia, no se puede rechazar la hipótesis nula, puesto que no hay evidencia suficiente para concluir que los datos no siguen una distribución normal [21]. En este caso, la hipótesis nula es verdadera y se considera que los residuos siguen una distribución normal. La distribución normal de los residuos también puede evaluarse gráficamente, a partir de la gráfica de probabilidad normal de residuos. Si la distribución es normal, dicha gráfica debe seguir una tendencia lineal. Para comprobar que no hay datos asimétricos o que se incluyan valores atípicos, se utiliza el histograma de residuos. La asimetría se refleja mediante largas colas en dirección, y los valores atípicos se presentan cuando hay algunas barras muy alejadas de las otras [21]. Ambas condiciones son indeseables en la regresión. En cuanto a la varianza constante para los residuos, se verifica a partir de la gráfica de dispersión de residuos versus ajustes. En dicha gráfica, los puntos deben ubicarse aleatoriamente a ambos lados de la escala horizontal, con patrones no detectables en los puntos [21]. Si los tres supuestos descritos se pueden satisfacer, la correlación es confiable y se puede proponer una ecuación entre las variables correlacionadas.
Gráficas de dispersión para CBR en estado natural
Las figuras 1, 2 y 3 presentan gráficas de dispersión para el CBR natural versus el límite líquido, el índice de plasticidad y la resistencia a compresión inconfinada, respectivamente. En las figuras 1 y 2 (límite líquido e índice de plasticidad), se puede apreciar que las nubes de puntos son muy dispersas y no muestran una tendencia clara, por lo que se puede establecer que para los suelos analizados no existe una buena correlación entre el CBR natural y el límite líquido o el índice de plasticidad. En la figura 3, que relaciona el CBR natural con la resistencia a compresión inconfinada, se puede ver que la nube de puntos está mejor agrupada y sigue una tendencia aproximada de tipo lineal, por lo que resulta conveniente realizar un análisis más detallado para determinar alguna correlación entre estas dos variables.
Gráficas de dispersión para CBR en estado saturado
Las figuras 4, 5 y 6 muestran gráficas de dispersión de CBR saturado con el límite líquido, el índice de plasticidad y la resistencia a la compresión inconfinada, respectivamente. Al igual que para el CBR en estado natural, en las figuras 4 y 5 (límite líquido e índice de plasticidad) se aprecia que la nube de puntos es muy dispersa y no hay una tendencia definida. Debido a lo anterior, se puede establecer que el CBR en estado saturado no presenta relación con el límite líquido y el índice de plasticidad. En la figura 6, que ilustra el CBR saturado versus la resistencia a la compresión inconfinada, se puede ver que la nube de puntos sufre una leve dispersión si se compara con la misma gráfica para el CBR natural (figura 3), pero sigue cierta tendencia y puede ser analizada estadísticamente para encontrar alguna relación entre estos dos parámetros.
Aunque no se incluyen debido a limitación de espacio, se prepararon gráficas de dispersión compuestas del límite líquido y el índice de plasticidad versus el CBR; del límite líquido, índice de plasticidad y contenido de finos versus el CBR; y del límite líquido, índice de plasticidad y humedad natural versus el CBR. El comportamiento fue similar al mostrado en las figuras 1, 2, 4 y 5; i. e., no se encontró una adecuada correlación entre estas combinaciones y el CBR, o al menos no fue tan clara como para la resistencia a la compresión inconfinada. Para esta, que mostró una mejor correlación con el CBR natural y saturado, también se evaluó si existe alguna relación específica, es decir, si hay tendencias diferentes con el CBR para cada tipo de suelo (limo o arcilla) o de compresibilidad (alta o baja). Se encontró que ni el tipo de suelo ni su compresibilidad afectan la relación entre la resistencia a la compresión inconfinada y el CBR; i. e., las tendencias son similares cuando se incluyen todas las muestras o cuando se analizan por separado limos y arcillas, o suelos de alta y baja compresibilidad.
Modelos de regresión para CBR natural versus compresión inconfinada
Después de verificar que el tipo de suelo y su compresibilidad no influyen en los resultados, se evaluaron modelos de regresión para encontrar una correlación entre el CBR y la compresión inconfinada, que sea aplicable para cualquier tipo de suelo y compresibilidad. Se utilizó el paquete estadístico Minitab [21]. En esta sección, se discuten estos modelos de regresión para el CBR natural.
Regresión lineal simple para CBR natural
Se plantea la ecuación (2) para el análisis estadístico, y las figuras 7, 8 y 9 muestran las gráficas de probabilidad normal, el histograma de residuos y la dispersión de residuos versus ajustes, respectivamente.
donde y es el CBR natural, x 1 es la compresión inconfinada, β 0, β 1 , son coeficientes por estimar y ε es el error.
En la gráfica de probabilidad de residuos ilustrada en la figura 7, se obtiene un valor P = 0,225>0,05, lo que significa que como hipótesis nula los residuales tienen distribución normal. Dicha figura sigue una tendencia lineal, por lo que se corrobora la distribución normal de los residuos. En la figura 8, no se observan largas colas en dirección o barras muy alejadas, por esta razón no hay asimetría o valores atípicos. Sin embargo, debido a que la gráfica de dispersión de residuos versus ajustes, ilustrada en la figura 9, muestra un cambio en la dispersión de la nube de puntos en forma de embudo abierto hacia afuera, el supuesto de varianza constante no se cumple, no hay homogeneidad en la distribución de la nube de puntos, de modo que la regresión lineal propuesta no es adecuada. Es necesario entonces realizar una transformación a la variable de respuesta para mejorar el modelo. Se evaluaron transformaciones utilizando el logaritmo y la raíz cuadrada del CBR, y se obtuvieron mejores resultados con la transformación mediante raíz cuadrada, como se describe a continuación.

Fuente: Elaboración propia.
Figura 7 Probabilidad normal de residuos: CBR natural versus compresión inconfinada.

Fuente: Elaboración propia.
Figura 8 Histograma de residuos: CBR natural versus compresión inconfinada.
Transformación de CBR natural que utiliza raíz cuadrada
Se propone transformar los valores de CBR natural a partir de la ecuación (3), y se preparan las gráficas de probabilidad normal, histograma y dispersión de residuos versus ajustes, como se ilustra en las figuras 10, 11 y 12, respectivamente.
donde  es la transformación del CBR natural mediante la raíz cuadrada.
es la transformación del CBR natural mediante la raíz cuadrada.
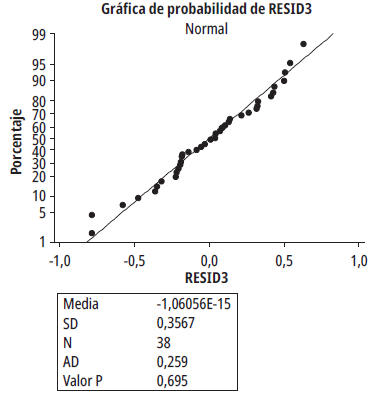
De la gráfica de probabilidad de residuos ilustrada en la figura 10, se obtuvo un valor P =0,695>0,05, es decir, que como hipótesis nula los residuales tienen distribución normal. Dicha figura sigue una tendencia lineal, lo que comprueba la distribución normal de los residuos. A partir del histograma de los residuos ilustrado en la figura 11, no se observan valores atípicos o asimétricos. De la gráfica de dispersión de residuos versus ajustes, ilustrada en la figura 12, se puede apreciar que la nube de puntos alrededor de 0 no presenta cambios en su dispersión, lo que satisface el supuesto de varianza constante. Debido a que se cumplen los tres supuestos, se concluye que el modelo realizado es apropiado. La tabla 2 presenta los resultados de dicho modelo, y se propone la ecuación (4) para obtener el CBR natural en función de la resistencia a la compresión inconfinada.
Fuente: Elaboración propia.
Figura 10 Probabilidad normal de residuos: raíz cuadrada CBR natural versus compresión inconfinada.

Fuente: Elaboración propia.
Figura 11 Histograma de residuos: raíz cuadrada CBR natural versus compresión inconfinada.

Fuente: Elaboración propia.
Figura 12 Dispersión de residuos versus ajustes: raíz cuadrada CBR natural versus compresión inconfinada.
Tabla 2 Resultado del análisis de regresión: raíz cuadrada CBR natural versus compresión inconfinada
| Predictor | Coef. | SE coef. |
|---|---|---|
| Constante | 1,229 | 0,101 |
| Comp. inconfinada | 0,609 | 0,0461 |
| Correlación de Pearson: raíz CBR natural versus compres. inconfinada = 0,911 | S = 0,36 r-cuad. = 0,829 r-cuad. (ajustado) = 0,824 |
Coef.: coeficiente de regresión; SE coef.: error estándar del coeficiente de regresión; S: desviación estándar; r-cuad.: coeficiente de determinación.
Fuente: Elaboración propia.
donde CBR nat es el CBR (%) bajo condiciones de humedad natural y qu es la resistencia a la compresión inconfinada (kg/cm2).
Modelos de regresión para CBR saturado versus compresión inconfinada
Se prepararon gráficos de probabilidad normal de residuos, histograma de residuos y dispersión de residuos versus ajustes para el CBR sin transformar y para la raíz cuadrada del CBR, sin obtener adecuados resultados para definir la correlación. Los mejores resultados para el CBR saturado se obtuvieron con la transformación mediante el logaritmo, como se describe en detalle a continuación.
Transformación de CBR saturado que utiliza logaritmo
Se plantea la ecuación (5) para la transformación, y las gráficas de probabilidad normal de residuos, histograma de residuos y dispersión de residuos versus ajustes se ilustran en las figuras 13, 14 y 15, respectivamente.
donde Log(y sat ) es la transformación del CBR saturado mediante el logaritmo.
De la gráfica de probabilidad de residuos ilustrada en la figura 13, se obtiene el valor P = 0,304>0,05, lo que significa que como hipótesis nula los residuales tienen distribución normal. No se observan valores asimétricos o atípicos en el histograma de residuos ilustrado en la figura 14. La varianza constante se verifica en la gráfica de dispersión de residuos versus ajustes, ilustrada en la figura 15, en la que se puede observar que la nube de puntos no presenta cambios de dispersión, por lo que muestra homogeneidad en su distribución. Los resultados del análisis estadístico se incluyen en la tabla 3, y se propone la ecuación (6) para obtener el valor del CBR saturado a partir de la resistencia a la compresión inconfinada.

Fuente: Elaboración propia.
Figura 13 Probabilidad normal de residuos: logaritmo CBR saturado versus compresión inconfinada.

Fuente: Elaboración propia.
Figura 14 Histograma de residuos: logaritmo CBR saturado versus compresión inconfinada.

Fuente: Elaboración propia.
Figura 15 Dispersión de residuos versus ajustes: logaritmo CBR saturado versus compresión inconfinada.
Tabla 3 Resultado del análisis de regresión: logaritmo CBR saturado versus compresión inconfinada
| Predictor | Coef. | SE coef. |
|---|---|---|
| Constante | 0,0479 | 0,0554 |
| Comp. inconfinada | 0,217 | 0,0252 |
| Correlación de Pearson: log CBR saturado versus compres. inconfinada = 0,820 | S = 0,198 r-cuad. = 0,672 r-cuad. (ajustado) = 0,663 |
Fuente: Elaboración propia.
donde CBR sat es el valor del CBR (%) en estado saturado y q u es la resistencia a la compresión inconfinada (kg/cm2).
Discusión
Aunque existe amplia información en la literatura sobre correlaciones del CBR con propiedades índice, como el límite líquido, el índice de plasticidad, el contenido de humedad o de finos, la densidad seca, entre otras (e. g., [16-17]), en muchas ocasiones, las correlaciones propuestas presentan una gran variabilidad con bajos coeficientes de correlación (r) o determinación (r 2). En la mayoría de los casos (e. g., [12,16-20]), estas correlaciones son obtenidas sin considerar el número adecuado de muestras desde el punto de vista estadístico. En esta investigación, a pesar de hallar cierta tendencia entre el CBR con variables como límite líquido, índice de plasticidad, contenido de finos y humedad natural (o bien de manera individual, o bien mediante combinaciones entre estas propiedades), se observó una importante dispersión en los datos. Por esta razón, este artículo se enfoca en las correlaciones obtenidas para determinar el CBR inalterado en condiciones de humedad natural y saturado como una función de la resistencia a la compresión inconfinada. Dichas correlaciones, indicadas en las ecuaciones (4) y (6), mostraron una tendencia bien definida, con coeficientes de determinación (r 2 ) igual a 0,83 y 0,67, para el CBR natural y saturado, respectivamente. Estos coeficientes son bastante adecuados para investigaciones experimentales en ingeniería geotécnica, en especial considerando la cantidad de muestras analizadas (38) y que las correlaciones son aplicables a cualquier tipo de suelo fino (limos o arcillas) de alta o baja compresibilidad. Los coeficientes de correlación de Pearson (r) obtenidos fueron de 0,91 y 0,82, respectivamente. Dichos coeficientes son mayores que el coeficiente usado para calcular el número mínimo de muestras (r = 0,60), lo que significa que el número de muestras analizadas es adecuado desde el punto de vista estadístico, y las correlaciones propuestas son estadísticamente confiables.
Existen en la literatura pocas referencias sobre correlaciones del CBR con la resistencia al esfuerzo cortante, en especial para suelos de grano fino. A través de una amplia revisión de literatura realizada antes de preparar este artículo, no se encontraron correlaciones entre el CBR de laboratorio de muestras de suelo fino inalteradas y la resistencia a la compresión inconfinada. Se encontró alguna información con ensayos de resistencia al corte, en especial triaxiales tipo no consolidado no drenado (UU, por sus siglas en inglés), realizados sobre muestras reconstituidas de suelos granulares o mezclas de suelos granulares y suelos finos [12,19]. También se halló una correlación del CBR sobre muestras inalteradas de grano fino y su resistencia al corte determinada mediante penetrómetro de bolsillo, con lo cual los resultados de resistencia al corte pueden presentar grandes variaciones [20].
[18] en 1961 propuso que la resistencia a la penetración del pistón del molde CBR podría ser relacionada con la capacidad portante. [18] afirmó que, a pesar de que el CBR es una medida del módulo de deformacion del suelo, en la práctica se había evidenciado que el esfuerzo necesario para penetrar el pistón hasta la profundidad mínima requerida (0,1") estaba relacionado con su capacidad portante última.
Posteriormente, [19] en 1979 investigaron la resistencia de subrasantes de arcilla y su relación con la humedad, plasticidad y CBR. Para arcillas remoldeadas, a partir de modelos de estudios de zapatas realizados por [30] en 1951, se encontró que el esfuerzo requerido para penetrar el pistón CBR era igual a la mitad de la capacidad portante última del suelo, y propusieron la ecuación (7) para obtener el CBR en función de la resistencia no drenada. En el mismo año, [20], a partir del estudio de la resistencia de arcillas inalteradas usando un penetrómetro, sugirió que el esfuerzo requerido para penetrar el pistón CBR era igual a la capacidad última del suelo, y propuso la ecuación (8) para calcular el CBR de muestras inalteradas de arcillas sobreconsolidadas. Recientemente, en 2007, [12] también sugirieron que el CBR es igual a la capacidad portante última del suelo; no obstante, se verificó su aplicabilidad para muestras reconstituidas, y no para muestras inalteradas, como lo propuso [20].
donde S u es la resistencia no drenada del suelo (kPa).
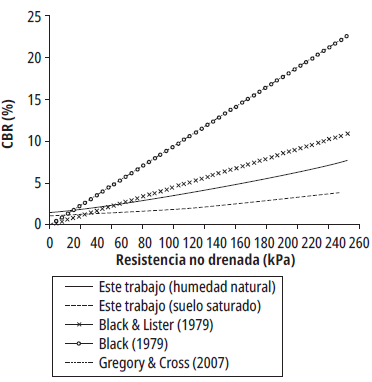
La figura 16 presenta una comparación de las correlaciones encontradas en nuestra investigación con respecto a las sugeridas para suelos finos por [12,19-20]. A pesar de que en nuestro estudio se encontraron valores de q u hasta de 650 kPa, la comparación en la figura 16 solo se realiza hasta valores q u = 250 kPa (consistencia muy firme a dura), debido a que fue el máximo valor encontrado en los ensayos de laboratorio discutidos en algunas de las referencias usadas para la comparación y a que es un adecuado límite superior de resistencia al corte para la mayoría de los subrasantes naturales con suelos de grano fino.
Fuente: Elaboración propia.
Figura 16 Comparación correlaciones entre CBR y resistencia no drenada en este estudio con correlaciones existentes en la literatura.
En la figura 16, se pueden observar diferencias importantes entre las correlaciones encontradas en la literatura, con respecto a las halladas en esta investigación. Aunque para valores de q u menores de 20 kPa (CBR<2%) las diferencias no son muy notorias, estas se acentúan cuando se incrementa la consistencia, con valores más bajos obtenidos en nuestra investigación. Por ejemplo, en suelos de consistencia media a firme (50 kPa<qu<100 kPa), los CBR obtenidos en este estudio son hasta tres y cuatro veces menores (humedad natural y saturado, respectivamente) que los sugeridos por [12] o por [20]. Cuando la consistencia del suelo aumenta (q u >100 kPa), la proporción de las diferencias en general se mantiene para el suelo con humedad natural e incrementa un poco para el caso saturado (tres y cinco veces, respectivamente). En términos del valor de CBR [12,20], pueden arrojar CBR hasta el 20% mayor que los hallados en esta investigación (aproximadamente el 24% versus el 4%), cuando la consistencia del suelo es de muy firme a dura (qu≥250 kPa).
De las correlaciones encontradas en la literatura, la que presenta valores más cercanos a los hallados en este estudio es la propuesta por [19] en 1979 para muestras remoldeadas. Para qu ≠250 kPa, esta correlación arroja valores aproximandamente 1,5 y 2,5 veces mayores (humedad natural y saturado, respectivamente) que los hallados en este estudio. Estas diferencias disminuyen para suelos con menor consistencia. No obstante, debe resaltarse que [19] sugirieron que esta ecuación debería usarse para muestras alteradas, y en nuestro estudio las muestras investigadas fueron inalteradas. Como se mencionó, para la correlación encontrada en la literatura para muestras inalteradas sobreconsolidadas, [20] sugiere valores hasta cinco veces mayores que los encontrados. Aunque en esta investigación no se evaluó el grado de sobreconsolidación de las muestras, para las resistencias en las que las diferencias se vuelven más importantes (q u >100 kPa), las muestras también deben haber tenido un alto grado de sobreconsolidación, dada la alta relación entre la resistencia no drenada y el esfuerzo efectivo (Su/s'vo>5); i. e., las muestras de mayor consistencia también eran sobreconsolidadas; sin embargo, se presentan grandes diferencias con respecto a [20].
La información presentada en la figura 16, y discutida, evidencia la importancia de tener una correlación específica para obtener el CBR inalterado de suelos finos de la región y del país, a partir de la resistencia a la compresión inconfinada. Las pocas correlaciones existentes entre el CBR y la resistencia al corte fueron obtenidas en otros lugares del mundo muchos años atrás o a partir de pocos ensayos sobre muestras remoldeadas o con penetrómetro de bolsillo. Se puede apreciar que en las tres correlaciones sugeridas para suelos de grano fino [12,19-20], los valores de CBR son mayores que los obtenidos en este estudio, en especial para suelos saturados con consistencia media o mayor. Por esta razón, usar dichas correlaciones en suelos de la región y del país sería poco conservador, y podría ponerse en riesgo el futuro desempeño de la estructura de pavimento. En esta investigación, incluimos limos y arcillas de alta y baja plasticidad con consistencia muy blanda a dura. Por lo anterior, la correlación propuesta puede usarse como un punto de partida para conocer la rigidez en estado inalterado de cualquier tipo de subrasante de suelo fino. Sin embargo, debe resaltarse que esta correlación podría no ser aplicable a suelos con medio o alto potencial de expansión, que no fueron encontrados en ninguno de los 38 sitios explorados.
Conclusiones y observaciones
En esta investigación, se estudiaron 38 muestras que involucraron limos y arcillas de alta y baja plasticidad, con consistencia entre muy blanda y dura. Los suelos fueron seleccionados para cubrir un amplio rango de propiedades, con límite líquido entre el 26 y el 93%, índice de plasticidad entre el 4 y el 57% y resistencia a la compresión inconfinada entre 0,10 y 6,6 kg/cm2.
Se encontraron dos correlaciones para obtener el CBR inalterado de suelos finos a partir de su resistencia a la compresión inconfinada. Para la transformación del CBR natural, se utilizó la raíz cuadrada, que permitió obtener un coeficiente de determinación (r 2) igual a 0,83. Para el CBR saturado, se utilizó el logaritmo, con el que el r 2 obtenido fue de 0,67. Es de esperarse que el coeficiente de determinación del CBR disminuya para el caso saturado, debido a que el ensayo de compresión in-confinada siempre se realiza bajo condiciones de humedad natural. Las correlaciones obtenidas son aplicables a cualquier tipo de suelo, independiente de su plasticidad, humedad o consistencia. Los coeficientes r 2 encontrados se consideran suficientemente adecuados para investigaciones experimentales en ingeniería geotécnica.
A pesar de que se intentó correlacionar el CBR, tanto en estado natural como saturado, con propiedades índice como los límites de Atterberg, humedad natural y contenido de finos, la tendencia entre las variables no fue tan buena como en la resistencia a compresión inconfinada, ni de forma individual ni para combinaciones entre ellas.
Las correlaciones obtenidas fueron comparadas con tres correlaciones propuestas en la literatura para suelos finos. La resistencia al corte en las correlaciones usadas para la comparación fue hallada mediante ensayos triaxiales tipo UU sobre muestras remoldeadas o a través de ensayos con penetrómetro sobre muestras inalteradas. No se encontró en la literatura alguna correlación entre el CBR de muestras inalteradas y su resistencia a la compresión inconfinada, como las propuestas en esta investigación. Las correlaciones halladas en la literatura mostraron valores de CBR inalterado considerablemente mayores que los obtenidos en este estudio. Debe resaltarse que en dichas correlaciones no se especifica si el CBR fue determinado en estado natural o saturado, lo que debería considerarse en subrasantes de suelos de grano fino.
Obtener correlaciones con un ensayo de relativa facilidad en la toma de muestra y en su realización, y soportadas por un análisis estadístico, constituye un aporte importante a la ingeniería geotécnica. Las correlaciones permiten obtener el CBR tanto en condiciones de humedad natural como saturado y son aplicables a cualquier tipo de suelo y plasticidad, lo que resalta aún más su importancia. Estas correlaciones pueden ser utilizadas como valores iniciales de prediseño en aquellos lugares donde no es posible tomar muestras inalteradas para CBR o para expandir la información de sitios donde se pueden realizar estos ensayos. La información obtenida debe ser verificada, al menos durante el proceso constructivo, después de efectuar el movimiento de tierras, en caso de no haber llevado a cabo ensayos durante el diseño.