Introducción
Los métodos empíricos para el diseño de pavimentos, basados en valores de California Bearing Ratio (CBR) como estimativo de resistencia, se desarrollaron a partir de las experiencias en vías existentes o en proyectos de investigación de gran envergadura, como el AASHO Road Test; mientras que los métodos mecanicistas, que usan el módulo resiliente (Mr) como parámetro de diseño, requieren un entendimiento teórico para lograr extender su aplicación a diferentes condiciones [1]. Estudios realizados por autores como Uzan [2], Carvalho y Schwartz [3] y Mashayekhi et al. [4] han evaluado las ventajas de emplear métodos que parten de la medida del Mr en lugar del CBR para el diseño de pavimentos. Estos estudios han demostrado que el diseño con métodos empíricos da como resultado, generalmente, estructuras más robustas de lo necesario o, en otras palabras, que existe un sobredimensionamiento de las mismas. Mashayekhi et al. [4] demostraron que los espesores de las capas del pavimento pueden llegar a ser hasta 33 % mayores.
No obstante lo anterior, muchos países, particularmente los países en desarrollo, todavía utilizan métodos de diseño que tienen un gran componente empírico, debido a que los procedimientos de diseño analíticos o mecanicistas más sofisticados requieren a menudo suposiciones con respecto al comportamiento del material, y los ensayos para obtener los parámetros de diseño no son de uso rutinario, debido a que los equipos para su ejecución no son fácilmente asequibles [5]. En otras palabras, los ensayos cíclicos que permiten determinar el Mr son relativamente complejos, los equipos son costosos, su disponibilidad es limitada y su ejecución consume una cantidad de tiempo considerable [6], [7], además de requerir personal capacitado.
Investigaciones sobre la respuesta de los suelos ante cargas cíclicas han impulsado el deseo y la necesidad de obtener el valor de Mr de manera económica y sencilla, con el objetivo de generar menor incertidumbre en el diseño de pavimentos, con respecto a las metodologías de base empírica [6]. Este problema se ha estudiado para desarrollar métodos alternativos y determinar el Mr [1], [8], [9]. Dentro de estos métodos se encuentra uno que propone la modificación o extensión del ensayo de CBR, ajustado para simular las cargas cíclicas a las que está sometido un pavimento, conocido como ensayo CBR cíclico (CCBR), con el cual se obtiene el módulo equivalente (E equi ) [2], [1], [8], [9].
En el presente artículo se muestran los resultados de E equ¡ para la caracterización mecánica de suelos blandos de subrasante típicos de la zona lacustre de Bogotá, mediante el ensayo de cCBR adaptado de las pruebas propuestas por Araya [1] y Sas et al. [6], comparados con los valores de Mr obtenidos sobre muestras idénticas en ensayos triaxiales aplicando la norma INV-156-13 "Módulo resiliente de suelos y agregados", cuya norma de referencia es la AASHTO T-307 "Standard Method of Test for Determining the Resilient Modulus of Soils and Aggregate Materials".
Ensayo CBR cíclico (CCBR)
El principio del ensayo CCBR es utilizar el equipo de CBR convencional, pero aplicando cargas repetitivas hasta llegar a un estado en el cual la deformación permanente sea nula o despreciable. Es decir, se trata de una extensión del ensayo de CBR (figuras 1a y 1b) dado que generalmente se emplean el mismo molde, la misma velocidad de aplicación de la carga (1.27 mm/min), el mismo pistón (49.64 mm de diámetro) y la misma cantidad de pesas de sobrecarga de 2.27 kg aproximadamente cada una (mínimo dos) [1], [6].

Fuente: elaboración propia.
Figura 1 Ensayo CCBR. (a) Deformación en función de la carga. (b) Desarrollo de las deformaciones con los ciclos de carga. (c) Deformación en función del tiempo. (d) Carga en función del tiempo
De manera más detallada, el ensayo de CCBR consiste en utilizar tres muestras inalteradas idénticas, contenidas en moldes de CBR, y penetrar cada una de ellas a una profundidad diferente (alrededor de 2.54 mm, 1.27 mm y 0.625 mm), registrando el esfuerzo requerido para alcanzar esa profundidad; este esfuerzo se aplica y se retira de manera repetida durante al menos 100 ciclos a una velocidad de 1.27 mm/min, hasta alcanzar un comportamiento resiliente, donde la variación en la deformación permanente entre ciclos consecutivos es menor a 3 %. Para asegurar un contacto permanente entre la muestra y el pistón, en el proceso de descarga se llega a una carga equivalente de cerca del 10 % de la registrada para la penetración objetivo (figuras 1c y 1d). La deformación resiliente que se utiliza para los análisis corresponde al promedio de las presentadas en los últimos cinco ciclos de ensayo.
Del CCBR se determina el E equ¡ , que representa una medida promedio de la rigidez de una muestra a niveles de esfuerzo superiores a los aplicados en un ensayo triaxial cíclico. Opiyo [10] desarrolló tres ecuaciones para estimar ese módulo en función del esfuerzo aplicado y la deformación recuperable: una de ellas es una ecuación empírica que asume que la deformación elástica ocurre en una parte cónica y en una parte cilíndrica, siendo la deformación total la suma de ambas (figura 2); otra es una simulación de elementos finitos, en la cual se asume una fricción total entre el molde y la muestra; y la última es una simulación que establece un deslizamiento total entre el molde y el suelo. Adicionalmente, cabe resaltar que las simulaciones aquí trabajadas utilizan un estrecho rango de propiedades elásticas (relación de Poisson y módulo de elasticidad) para obtener los resultados.

Fuente: Araya [1].
Figura 2 Deformación cónica y cilíndrica en la solución aproximada para calcular el módulo mediante el CCBR
Dentro de las limitaciones de estas técnicas de estimación del E equ¡ se encuentra el hecho de que se debe asumir un ángulo de distribución de la carga en la parte cónica para el caso de la solución aproximada, y que la condición real entre el molde y el suelo no es de fricción total ni tampoco de desplazamiento total en el caso de las simulaciones por elementos finitos.
Partiendo de la segunda limitación, Araya [1], utilizando también modelaciones con elementos finitos, propone una ecuación en la que se tiene una condición más ajustada entre el molde y el espécimen. Además, las muestras de suelo consideradas en la simulación van desde materiales granulares de muy buena calidad hasta marginales, con el objetivo de considerar una amplia gama de propiedades elásticas.
Dada las mejoras evidentes presentadas por esta última propuesta, resultado de un análisis más ajustado a la condición real del material, se consideró como la más adecuada para determinar el E equ¡ en el presente estudio.
La expresión propuesta por Araya [1] se presenta en (1), donde E equ¡ es el módulo equivalente en MPa, α es el radio del pistón de penetración en mm, w es la deformación resiliente promedio de los últimos cinco ciclos del ensayo en mm, σ p es la presión aplicada por el pistón (resta entre la presión aplicada y la de contacto) en MPa y v es la relación de Poisson; esta última se establece como 0.45, puesto que es un valor considerado típico para los suelos arcillosos de subrasante encontrados en la zona lacustre de Bogotá.
En este estudio, la toma de datos de carga y deformación se realizó mediante un sistema de adquisición de datos compuesto por una celda de carga tipo S, un transductor de desplazamiento y un software desarrollado en LabviEW, tal como se observa en las figuras 3 y 4.
Los módulos equivalentes obtenidos en los tres ensayos realizados sobre muestras de la misma exploración permiten determinar su dependencia de los niveles de esfuerzo y, por tanto, se pueden comparar y validar modelos constitutivos obtenidos mediante este ensayo y el de Mr, que se realiza en una prueba triaxial de carga cíclica, tal como la expuesta en la norma INV-156-13 "Módulo resiliente de suelos y agregados".
Los modelos constitutivos seleccionados en el estudio corresponden al modelo k - σ d (2) y al modelo universal (3), que tienen en cuenta el esfuirzo deiviador, que se ha revelado como e 1 parámetro más influyente en el módulo de suelos arcillosos blandos [11], [12].
Aquí, M r es el módulo resiliente en MPa, Pa es la presión atmosférica (establecida como 102 kPa en Bogotá), σ d es el esfuerzo desviador en MPa, θ el esfuerzo bulk en MPay T oct elcortante octaédrico en MPa.
Cabe aclarar que, aunque en el estudio se trabajaron ambos modelos, en el presente documento únicamente se reportan los resultados obtenidos de la comparación del modelo k - σ d , debido a que el análisis estadístico utilizado únicamente puede ser empleado en ecuaciones que dependan de una sola variable, en este caso σ d (el modelo universal depende del θ y de Toct).
Metodología
Se realizaron perforaciones en diferentes lugares de la zona lacustre de Bogotá, área establecida por mapas del Decreto 523 de 2010 [13], donde se tomaron muestras a profundidades comprendidas entre 0.4 y 2.0 metros. En algunos casos, para encontrar los estratos de suelos blandos de este estudio, fue necesario atravesar capas de materia orgánica y rellenos construidos con anterioridad para nivelar el terreno.
En la tabla 1 se presentan los resultados de la caracterización física y mecánica (CBR sobre muestra inalterada) de las muestras obtenidas de cada una de las exploraciones. Tal como se observa, en el estudio se incluyeron muestras de arcilla y de limo de alta compresibilidad (CH-MH) y limos de baja compresibilidad (ML) que, en algunos casos, tenían raíces y trazos de materia orgánica (figura 5). En general, los suelos analizados tienen valores de Gs comprendidos entre 2.68 y 2.72, y un grado de saturación entre el 86 % y el 96 %, valores típicos a las profundidades evaluadas de suelos que se encuentran en zona lacustre [14], [15].

Fuente: fotografías de los autores.
Figura 5 Muestras con presencia importante de raíces y materia orgánica
Tabla 1 Montaje de celda de carga y transductor de desplazamiento
| Explo. | Prof. (m) | Humedad (%) | Peso unitario total (kN/m3) | e | Pasa n.° 200 (%) | LL (%) | IP (%) | SUCS | CBR1 ** (%) | CBR2 + (%) * |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.30 - 1.50 | 45 | 16.94 | 1.28 | 100 | 94 | 62 | CH | 2.5 | - |
| 2 | 1.20 - 1.40 | 46 | 16.97 | 1.29 | 100 | 98 | 69 | CH | 2.4 | - |
| 3 | 1.60 - 1.80 | 60 | 15.43 | 1.76 | 98 | 97 | 66 | CH | 1.8 | - |
| 4 | 0.80 - 1.00 | 82 | 13.96 | 2.42 | 54 | 46 | 6 | ML | 4.9 | 3.4 |
| 5 | 1.20 - 1.40 | 47 | 16.61 | 1.35 | 99 | 96 | 65 | CH | 4.0 | - |
| 6 | 1.00 - 1.20 | 61 | 15.72 | 1.74 | 99 | 99 | 69 | CH | 1.5 | 1.1 |
| 7 | 0.80 - 1.00 | 63 | 15.53 | 1.78 | 99 | 90 | 59 | CH | 1.7 | - |
| 8 | 0.50 - 0.80 | 102 | 12.68 | 3.21 | 70 | 129 | 57 | MH | 5.1 | 2.2 |
| 9 | 0.50 - 0.80 | 82 | 13.45 | 2.55 | 79 | 132 | 60 | MH | 3.4 | 3.3 |
| 10 | 0.50 - 0.80 | 96 | 13.32 | 2.87 | 61 | 125 | 66 | MH | 3.9 | 3.6 |
| 11 | 0.50 - 0.70 | 95 | 13.77 | 2.72 | 52 | 122 | 55 | MH | 4.0 | 3.5 |
| 12 | 0.60 - 0.80 | 107 | 13.41 | 3.05 | 53 | 125 | 50 | MH | 2.7 | 2.6 |
| 13 | 0.40 - 0.60 | 103 | 13.53 | 2.98 | 57 | 114 | 46 | MH | 3.2 | 2.2 |
| 14 | 0.50 - 0.70 | 89 | 13.30 | 2.73 | 59 | 120 | 53 | MH | 4.2 | - |
| 15 | 1.80 - 2.00 | 69 | 15.29 | 1.93 | 99 | 79 | 50 | CH | 1.7 | - |
| 16 | 0.50 - 0.70 | 109 | 13.37 | 3.16 | 53 | 132 | 68 | MH | 3.6 | 1.2 |
| 17 | 0.50 - 0.70 | 111 | 13.42 | 3.18 | 59 | 97 | 31 | MH | 4.4 | 3.0 |
| 18 | 0.40 - 0.70 | 85 | 14.55 | 2.34 | 51 | 104 | 49 | MH | 4.5 | 4.4 |
| 19 | 0.40 - 0.70 | 91 | 14.17 | 2.57 | 51 | 109 | 51 | MH | 3.6 | - |
** CBR muestra inalterada
+ CBR después de cuatro días
*- indica que no se realizó el ensayo
Fuente: elaboración propia.
También es posible resaltar que algunos valores de peso unitario total corroboran la presencia de materia orgánica detectada con la simple observación del material (figura 5), y que la presencia de arenas contribuye a valores de CBR superiores. Los valores de CBR no superan el 5 %, incluso aquellos obtenidos sobre las muestras antes de inmersión en agua, lo que era de esperar debido a la consistencia blanda de los suelos de la zona lacustre de la ciudad [16], [17]. Cabe resaltar que en los ensayos en los que las muestras se sometieron a inmersión, no se registró expansión.
Resultados
Tal como se presenta en (2), en el modelo k - σ d el esfuerzo desviador es el único atributo para evaluar el comportamiento del módulo. Con el fin de validar los resultados obtenidos del ensayo de cCBR para hallar valores de Mr, el procedimiento consistió en hacer uso del análisis de regresión.
En este documento se presentan únicamente algunos de los resultados, considerados representativos del buen ajuste obtenido en general, correspondientes a las muestras de menor y mayor humedad (exploraciones 1 y 17), peso unitario (exploraciones 8 y 2), contenido de arena (exploraciones 1 y 18) e índice de plasticidad (exploraciones 4 y 6). Los valores de Mr y E equ¡ encontrados se muestran en las tablas 2 y 3, respectivamente.
Tabla 2 Mr (en MPa) del ensayo triaxial cíclico INV - E - 156 - 13
* Esfuerzos en kPa
Fuente: elaboración propia.
Tabla 3 E equi (en MPa) para diferentes penetraciones ensayo CCBR
| Valores de E equi (en MPa) | ||||
|---|---|---|---|---|
| Pen. (mm) | 2.54 | 1.27 | 0.625 | |
| Exploración | 1 | 31.4 | 29.4 | 26.7 |
| 2 | 31.7 | 29.5 | 28.6 | |
| 4 | 19.5 | 14.8 | 14.1 | |
| 6 | 32.8 | 32.5 | 29.3 | |
| 8 | 18.7 | 15.4 | 14.2 | |
| 17 | 24.3 | 23.2 | 16.9 | |
| 18 | 24.1 | 13.8 | 13.4 | |
Fuente: elaboración propia.
El análisis comienza con la determinación de la calidad de un buen ajuste estadístico, que según Rehman et al. [18] se consigue con un R2>0.7; de manera general, para todas la exploraciones realizadas, al evaluar el comportamiento del Mr y del E equ¡ respecto a σ d se obtienen R2 superiores a dicho estándar, tal como se advierte en la figura 6.

Fuente: elaboración propia.
Figura 6 Relación entre Mr y Eequi (CCBR) con el esfuerzo desviador de las muestras de mayor y menor. (a) Humedad. (b) Peso unitario. (c) % de arena. (d) Índice de plasticidad
Al observar los resultados p ara estos rangos de humedad, de pesos unitarios, de c ntenido de arena y de plasticidad, se puede decir que los valores del E equ¡ tienen correspondencia con los del Mr de los suelos que se obtienen a elevados niveles de esfuerzo, independientemente de sus características físicas.
Una vez establecida la buena correlación entre el módulo (resiliente o equivalente) y a d , se sabe que es viable el siguiente paso del análisis, que es determinar los intervalos de predicción. De acuerdo con Wonnacott y Wonnacott [19], este ejercicio consiste en la estimación de un intervalo de valores en el que se producirá una observación futura con determinada probabilidad, dado lo que ya se ha observado.
Para calcula r los intervalos de predicción, asumiendo que los datos de Mr y E equ ¡ utilizados se ajustan a una ddistribución normal, se hace uso de (4), donde m es la pendiente de la regresión, p el punto de corte con e 1 eje "y", n el número de datos (15 en este caso, que corresponden a los obtenidos en el ensayo de Mr), s es una constante calculada con (5), z es el nivel de confianza y x̅ es el promedio de los valores de σ d .
Para este caso particular, se realizó el análisis para determinar los intervalos de predicción, con un 95% de confiabilidad (z = 1,96), a partir de los resultados del ensayo de Mr (figura 7a); posteriormente, utilizando el modelo constitutivo k - σ d obtenido del ensayo de CCBR, se calculan los Mr a los mismos niveles de esfuerzo del ensayo Mr. Se considera que el modelo constitutivo presentado en el CCBR es adecuado para determinar el Mr a bajos niveles de esfuerzo, si dichos valores calculados caen dentro de los intervalos de predicción (figura 7b).
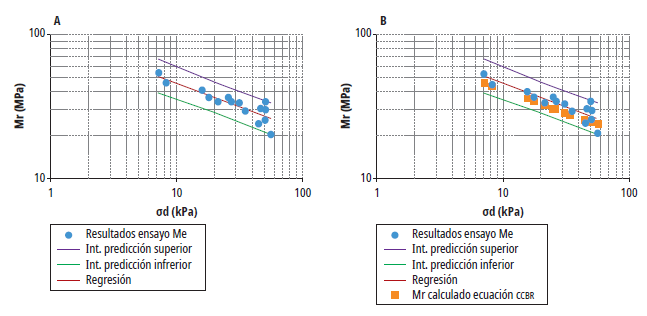
Fuente: elaboración propia.
Figura 7 Ejemplo gráfico, (a) Intervalos de predicción y regresión, (b) Ajuste de predicción de la ecuación constitutiva de CCBR
Así como se hizo con el ajuste estadístico, a continuación se presentan los resultados de los intervalos de predicción para las muestras de menor y mayor humedad, peso unitario, contenido de arena e índice de plasticidad (figura 8). Los resultados de estas muestras son representativos de los encontrados en todas las exploraciones ejecutadas.

Nota: se emplea la misma convención de colores de la figura 7b.
Fuente: elaboración propia.
Figura 8 Intervalos de predicción y validación del modelo k-σd del E equi del ensayo CCBR de las muestras de mayor y menor. (a) Humedad. (b) Peso unitario. (c) % de arena. (d) Índice de plasticidad
A partir de la figura 8 es posible observar que, como era de esperar, los suelos de subrasante estudiados presentan menores valores de módulo cuando la humedad aumenta y cuando el peso unitario disminuye [20]. Además, se puede establecer que, para las muestras evaluadas, a menor índice de plasticidad el módulo disminuye. Por otra parte, se resalta que la muestra que no contiene arena presenta, para igual a d , una mayor rigidez en comparación con aquella que contiene un elevado contenido de arena, lo que se atribuye a la presencia significativa de raíces en esta última. Por otra parte, las muestras con menor peso unitario tienden a ser las que tienen menos plasticidad y más arena, es decir, los limos.
También es posible establecer, a partir de la figura 8, que los valores de k 2 son similares en todas las muestras, exceptuando aquellas con menor peso unitario, lo que quiere decir que los suelos blandos de subrasante analizados en este estudio presentan una dependencia similar de su módulo con respecto a σ d . El hecho de que la muestra de menor peso unitario no registre esta misma dependencia podría atribuirse a la presencia de materia orgánica en este suelo, que además registra el menor valor de k x .
Finalmente, las ecuaciones constitutivas del E equ¡ obtenidas a partir del ensayo de CCBR permiten obtener un estimado del Mr con un 95% de confiabilidad, en diferentes condiciones de humedad, peso unitario, plasticidad y granulometría de los suelos blandos de subrasante. Lo anterior demuestra que la prueba de CCBR puede ser una opción viable para estimar Mr, ante la carencia de una infraestructura adecuada para ejecutar este ensayo.
Conclusiones
Los resultados muestran, en general, que es posible obtener los valores del Mr, determinados a niveles de esfuerzo más bajos, a partir de modelos constitutivos del E equi , con un buen nivel de predicción. Es decir, con el ensayo CCBR se puede tener una buena estimación del Mr de suelos blandos de subrasante, independientemente del tipo de suelo (arcilla o limo) y de su humedad, densidad, plasticidad e incluso de su granulometría; por tanto, esta prueba demuestra ser una opción viable, económica y sencilla, en ausencia de los equipos necesarios para la ejecución del ensayo triaxial cíclico definido por los estándares.
Adicionalmente, se puede observar que el E equi tiene correspondencia con el Mr que se obtendría a niveles de esfuerzo mayores a los que es sometida la muestra en un ensayo triaxial estándar. En caso de trabajar con ambos ensayos en simultáneo, es posible establecer un modelo constitutivo que abarque un mayor rango de esfuerzos.
Por otra parte, es importante resaltar que, a pesar de que el CCBR es una opción adecuada para estimar valores de rigidez, la ejecución de un ensayo de este tipo requiere más trabajo de campo y laboratorio que la de un ensayo triaxial cíclico, debido a que en la exploración se requiere la extracción de tres moldes inalterados de CBR por ensayo, en lugar de la obtenida con un tubo de pared delgada, y se necesita ejecutar tres veces el mismo procedimiento, algo que no ocurre en el ensayo de Mr. Sin embargo, su gran ventaja es que el equipo requerido es una prensa, que se encuentra en cualquier laboratorio donde se realicen ensayos de rutina, algo que no sucede con la máquina triaxial usada en el Mr.
Otro punto fundamental de cuidado en el ensayo CCBR es que el proceso de extracción de muestras debe hacerse con cuidado y teniendo la mayor proximidad posible entre las tres muestras, con el fin de que estas sean lo más similares posibles en sus propiedades, y así tenga validez el análisis de los resultados obtenidos.
Finalmente, los resultados obtenidos demuestran que la fórmula presentada por Araya (2011) [1] para el cálculo del E equi es adecuada, aun cuando se realizaron suposiciones respecto a la relación de Poisson, se recomendaría en futuras investigaciones incluir ensayos que permitan la determinación de tal parámetro, para refinar aún más los valores de E equi calculados.



















