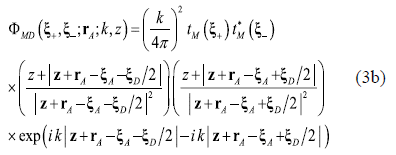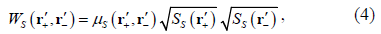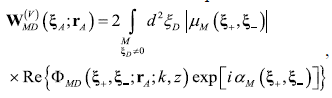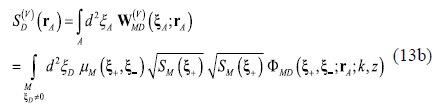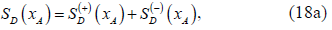Introduction
The wave superposition is the standard fundamental concept to explain interference and diffraction with classical waves and quantum particles. It plays the role of physical principle in the classical context (Born & Wolf, 1993), while in the quantum context, it is used as a mathematical procedure for the calculation of the spatial probability density associated to the particles (Feynman, et al., 1965).
The mathematical formalization of both contexts bases on the Helmholtz equations corresponding to the spatial or time-independent parts of the classical wave equation in free-space and the field-free Schrodinger's equation, respectively. The term "wave" names the complex valued eigen-functions of the Laplacian operator in the respective Helmholtz equation. In addition, the same terminology and mathematics is used for referring the results of the experiments, whose setups for waves and particles have the same configuration, differing only in scale.
However, the meanings of the term wave in such contexts are quite different. In classical optics, it describes the physical disturbance due to the electric field oscillations at each point in space. In quantum mechanics, it is called the complex amplitude of probability and its squared modulus determines the spatial probability density, i.e. it does not describe a physical disturbance. So, the wave superposition realizes the addition of disturbances of classical waves at each point of space but the determination of conditional probabilities to find the quantum particle at a given position.
These different interpretations of the wave superposition lead to the conclusion that interference of classical waves and quantum particles have not been explained from a common and unique physical principle. Moreover, the standard description of interference with single quantum particles, from electrons (Matteucci, et al., 2013) to molecules (Nairz, et al, 2003) (Juffmann, et al., 2012), requires the assumptions of wave-particle duality, self-interference and quantum wave collapse, which turn this explanation in a mystery in the heart of quantum mechanics (Feynman & Hibbs, 1965).
Then, the question arises on the pertinence of searching for a unique physical principle of interference and diffraction with classical waves and quantum particles. A more accurate mathematical model should be discarded as pertinence criterion, because the high accuracy of the standard formulation has been corroborated by its predictions of a wide variety of interference and diffraction experiments. Consequently, any alternative formulation should maintain the mathematical fundamentals of the standard one.
Technology and innovation development in both classical and quantum physics is neither a pertinence criterion. Contemporary nano- and micro-technologies widely use the so-called wave nature of matter in current applications (Capelli, et al., 2014). The theoretical development of quantum physics has not been hampered by the necessity of an alternative theory of interference and diffraction. Actually, the difficulties and limitations of the interference and diffraction description of quantum particles have been regarded as a point-feature or singularity of the quantum physics, i.e. "the only mystery in the heart of quantum mechanics".
Thus, the main pertinence criterion seems to be epis-temological, that is the challenge to solve this mystery by taking into account that only the necessary causes should be taken into account to explain physical phenomena and effects of the same kind should be attributed to the same cause. A successful response to that challenge should give more insight on the physics of interference and diffraction.
To this aim, a new description is proposed in the current paper. Its basic quantity is the two-point correlation, instead of the wave function, which is the basic quantity of the standard description. Although the two-point correlation was firstly used as basic quantity by the theory of optical coherence (Mandel & Wolf, 1995), an important difference between the new description and this theory is established. Indeed, the new description introduces a geometrical interpretation of the two-point correlation in close connection with the experimental setup configuration, section 2. In this context, the two-point correlation is contributed by the setup instead of being an attribute of the classical waves and the quantum wave functions, as assumed in the standard description (Mandel & Wolf, 1995). In addition, any experiment is modeled according to the P & M (preparation-measurement) scheme with two accessible states named the source-turn-off and the source turn-on states. Specifically, the experiments prepare two-point correlations in the source-turn-off state and measure energy distributions in the source-turn-on state.
The physical principle of the new description of interference and diffraction is discussed in section 3. It is not the wave superposition and does not require support hypotheses like wave-particle duality, self-interference and quantum wave collapse. Regardless the different technology scales of the interference and diffraction experiments with classical waves and quantum particles, both the setup design requirements and the mathematical description of the experiments are essentially the same, section 4. Its non-paraxial formulation can predict the spatial distribution of the wave or particle energy along distances from the source comparable to the wavelength (Castañeda, et al., 2016 a, b) (Castañeda, 2017 b), including polarization effects in case of electromagnetic waves (Castañeda, 2014) (Castañeda, 2016). So, the geometric model becomes an efficient tool for the development of very compact optical and quantum devices. In sections 5 and 6 some experimental evidences of its validity are discussed, and the conclusions are presented in section 7.
The geometric interpretation
The conceptual sketch in Figure 1 realizes the P & M scheme for any interference or diffraction experiment with classical waves or quantum particles.

Figure 1 Conceptual sketch of the setup for field-free or free-space interference or diffraction. S: source plane, M: mask plane, and D: detector plane. The shadowed circles on each plane represent the structured supports of spatial coherence, and the W-functions are the two-point correlations at the respective planes. Reduced coordinates, indicated by the arrows on each plane, specify the pairs of point in any structured support. The solid line cone in the SM-stage represents the prepared correlation cone, while the dotted line cone in the MD-stage represents the energy cone to be measured.
Reduced coordinates are adopted in order to specify the two-point correlation at each plane i.e. (r’A,r'
D
) for the S-plane, (ξA, ξD) Ό for the M-plane and (r
A
, r
D
) for the D-plane. They allow determining univocally pairs of points on the respective plane, equidistant from the point specified by the coordinate with suffix A, and with separation vectors given by the coordinate with suffix D, whose positions are then
 and
and
 respectively. Thus,
respectively. Thus,
 and
and
 denote the two-point correlation at the S, M and D planes respectively, of any pair of points symmetrically placed with respect to the center denoted by the coordinate suffixed A. The area around these centers outside which the two-point correlation values are negligible is called the structured support of correlation (Castañeda & Matteucci, 2017). Thus, the separation vectors of the pairs of points enclosed by any structured support are shorter than the support size. Such pairs of points are correlated in some extent, while those with longer separation vectors are non-correlated.
denote the two-point correlation at the S, M and D planes respectively, of any pair of points symmetrically placed with respect to the center denoted by the coordinate suffixed A. The area around these centers outside which the two-point correlation values are negligible is called the structured support of correlation (Castañeda & Matteucci, 2017). Thus, the separation vectors of the pairs of points enclosed by any structured support are shorter than the support size. Such pairs of points are correlated in some extent, while those with longer separation vectors are non-correlated.
It is known that the two-point correlation is the eigen-function of the Laplacian operators of two Helmholtz equations, with the same eigen-value (Mandel & Wolf, 1995). Its mathematical form can be determined by solving the Helmholtz equations by the Green's function method. It allows expressing the two-point correlation on a plane as the output of a time-independent modal expansion defined in the volume delimited by a previous input plane and the output plane, with the following features: (i) the expansion kernel is a set of volumetric scalar geometrical modes, defined by the boundary conditions of that volume, and (ii) the values of the two-point correlation at the input plane are the input of the modal expansion.
It is worth noting that the two-point correlation is, in general, a spatial non-local function, but includes local values specified by the null separation vectors. These local values determine the spatial distribution of the energy at the output plane once the source of waves or particles is put into operation. It allows characterizing the P & M scheme of the experiments as follows: (i) preparation in the SM-stage means the determination of the output two-point correlation at the M plane, given an input two-point correlation at the S plane; (ii) measurement in the MD-stage means the determination of the output spatial distribution for the energy at the D plane, given a prepared two-point correlation at the M plane as input. So, the mathematical formulation of the P & M scheme is realized by
for the prepared two-point correlation at the M-plane, and
fo r the spatial distribution for the energy to be measured at the D-plane. It is obtained by evaluating the two-point correlation at the D-plane for
 .
.
The integrands of Eqs. (1) are given by the non-paraxial modal expansions
And
respectively, with W S (r’+, r’_ ) the two-point correlation at the S-plane. The integration kernels in Eqs. (2) are the scalar, deterministic, non-paraxial and three-dimensional modes (Castañeda, 2017 b) (Castañeda & Matteucci, 2017)
defined in the volume of the SM-stage, and
defined in the volume of the MD-stage, where
And
are the complex transmissions of the S and the M- planes respectively. The quantities
 and
and
 are called the absorbance of the respective plane and determine the amount of the incident energy that crosses the plane (Born & Wolf, 1993). It is worth noting that the mode arguments denote the geometric features at the input and the output planes related by the modes. Indeed,
are called the absorbance of the respective plane and determine the amount of the incident energy that crosses the plane (Born & Wolf, 1993). It is worth noting that the mode arguments denote the geometric features at the input and the output planes related by the modes. Indeed,
 relates any structured support of correlation on the S-plane, specified by (r’+ ,r’-) to each structured support on the M-plane given by (
relates any structured support of correlation on the S-plane, specified by (r’+ ,r’-) to each structured support on the M-plane given by (
 ); while
); while
 relates any structured support of correlation on the M-plane to each point A rA on the detector at the D-plane. In this way, the modes in Eq.(3a) shape the space in the SM-stage in accordance to the stage boundary conditions, for the preparation of the two-point correlation at the M-plane; in turn, the modes in Eq.(3b) shape the space in the MD-stage in accordance to this stage boundary conditions, for the measurement of the power spectrum. It is worth remarking that the geometric modulation of the space provided by the modes in Eqs. (3) is independent from the physical and statistical properties of the source of waves or particles attached at the S-plane.
relates any structured support of correlation on the M-plane to each point A rA on the detector at the D-plane. In this way, the modes in Eq.(3a) shape the space in the SM-stage in accordance to the stage boundary conditions, for the preparation of the two-point correlation at the M-plane; in turn, the modes in Eq.(3b) shape the space in the MD-stage in accordance to this stage boundary conditions, for the measurement of the power spectrum. It is worth remarking that the geometric modulation of the space provided by the modes in Eqs. (3) is independent from the physical and statistical properties of the source of waves or particles attached at the S-plane.
The k parameter of the modes plays an important role in the geometric modulation of the space. It is related to the eigen-value _k 2 of the Laplacian operators in the Helmholtz equations solved by the two-point correlation, and can be expressed as k = 2π/λ, where λ denotes the length along which the exponential argument of the modes evolves in 2π. This length is essentially determined by the setup boundary conditions and explains the scale differences in the setup design for material particles (nanoscale) and waves (microscale at visible frequencies). For this reason, λ is called the space scale metric (Castañeda, 2017 b) (Castañeda & Matteucci, 2017).
Now, it is crucial to clarify the relationship of the space scale metric with the optical and the de Broglie wavelengths λ’, defined as physical attributes of waves and particles by the formulas λ’ν = c for a classical wave of frequency ν and free-space speed c, λ’E = hc for the photon of energy E, with h the Planck constant, and λ’ p = h for a quantum particle momentum p. It is worth remarking that the standard formulation does not make difference between λ and λ’, thus labelling both symbols with the term wavelength and its physical meanings, and regarding its geometrical feature as a secondary property. In this sense, the expressions above involving λ’ corroborate the wave nature of the quantum particles, thus supporting the assumption that interference and diffraction are distinctive behaviors of wave phenomena, including the quantum particles. In addition, k = 2π/λ'.
In contrast, the new interpretation (i) underlines the different meanings of λ and λ’ as equally important, and (ii) interprets the expression λ’ = λ as a coupling condition of the physical object (waves and particles) to the experimental setup, i.e. classical waves and quantum particles move according to the geometric modulation established by the modes of parameter k = 2π/λ only if their respective frequency, energy or momentum assure the achievement of the condition λ = λ’. Otherwise, their movement through the setup does not follow such geometric modulation. Because of these features, the new model proposes interference and diffraction as resulting from the geometric modulation of space determined by the setup configuration, instead of being the distinctive behaviors of wave phenomena. Furthermore, such features lead to the conclusion that interference and diffraction experiments should have the same configuration but different scales for classical waves and quantum particles, as widely reported in literature, for instance the double slit interference experiment in optics (Born & Wolf, 1993) and with single electrons (Matteucci, et al., 2013).
Now, let us analyze the meanings of Eqs. (2). They are modal expansions defined in the volumes of the SM- and the MD-stages respectively that describe the distributions of the respective input two-point correlations, W
S
(r’+, r’_) and
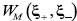 , over the geometric modes in the stages to give the prepared two-point correlation at the M-plane,
, over the geometric modes in the stages to give the prepared two-point correlation at the M-plane,
 , and the spatial distribution of the energy to be measured at the D-plane, S
D
(rA ). The input two-point correlations have energy units because they involve the energy distributions of the classical waves and the quantum particles at the corresponding planes, denoted by
, and the spatial distribution of the energy to be measured at the D-plane, S
D
(rA ). The input two-point correlations have energy units because they involve the energy distributions of the classical waves and the quantum particles at the corresponding planes, denoted by
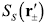 and
and
 respectively. In this way, the input two-point correlations include the physical and statistical attributes of the waves and particles moving in the setup. However, it is possible to analyze the pure geometrical (or energy independent) feature of interference and diffraction as follows.
respectively. In this way, the input two-point correlations include the physical and statistical attributes of the waves and particles moving in the setup. However, it is possible to analyze the pure geometrical (or energy independent) feature of interference and diffraction as follows.
Let us begin with the preparation of the two-point correlation in the SM-stage. The two-point correlation at the S-plane can be expressed as
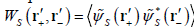 , with
, with
 and the asterisk denoting ensemble average and complex conjugate, respectively. The functions
and the asterisk denoting ensemble average and complex conjugate, respectively. The functions
 are the eigen-functions of the individual Helmholtz equations for the spatial coordinates r’±. They can be expressed as
are the eigen-functions of the individual Helmholtz equations for the spatial coordinates r’±. They can be expressed as
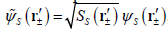 , where
, where
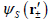 represents the geometric feature of the eigen-functions provided
represents the geometric feature of the eigen-functions provided
 . So
. So
 stands and therefore
stands and therefore
 as expected. On the other hand, W
S
(r’+,r’_) should Mfil the Schwarz inequality
as expected. On the other hand, W
S
(r’+,r’_) should Mfil the Schwarz inequality
 (Mandel & Wolf, 1995), which can be expressed as equation by introducing the appropriate dimensionless coefficient
(Mandel & Wolf, 1995), which can be expressed as equation by introducing the appropriate dimensionless coefficient
 on the right. Consequently, the two-point correlation takes the mathematical form
on the right. Consequently, the two-point correlation takes the mathematical form
provided
 with
with

 . From Eq. (4) follows
. From Eq. (4) follows
 , which is called the complex degree of correlation (Castañeda, 2017 b) (Castañeda & Matteucci, 2017) at S-plane. Its meaning can be established consistently from Eq. (4) that represents the spatial correlation of the emission of waves or particles by the source. The energy attributes of the emitted waves and particles are completely denoted by the factor
, which is called the complex degree of correlation (Castañeda, 2017 b) (Castañeda & Matteucci, 2017) at S-plane. Its meaning can be established consistently from Eq. (4) that represents the spatial correlation of the emission of waves or particles by the source. The energy attributes of the emitted waves and particles are completely denoted by the factor
 , while the complex degree of correlation involves only the geometric component of the eigen-functions. So,
, while the complex degree of correlation involves only the geometric component of the eigen-functions. So,
 denotes the spatial correlation between pairs of emitting points at the S plane as the geometrical (or energy independent) feature of W
S
(r’+, r’_). It is worth remarking the theoretical consistency of this interpretation, because it gives new insight to the meaning established in partially coherent optics as the measurement of the spatial correlation of the emitted waves (Mandel & Wolf, 1995).
denotes the spatial correlation between pairs of emitting points at the S plane as the geometrical (or energy independent) feature of W
S
(r’+, r’_). It is worth remarking the theoretical consistency of this interpretation, because it gives new insight to the meaning established in partially coherent optics as the measurement of the spatial correlation of the emitted waves (Mandel & Wolf, 1995).
The complex degree of correlation exhibits the following mathematical properties: (i)
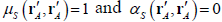 , (ii)
, (ii)
 and (iii) its support around a given point r’A is just the structured support of correlation centered at such position.
and (iii) its support around a given point r’A is just the structured support of correlation centered at such position.
Now, let us analyze the pure geometrical (or energy independent) feature of the preparation SM-stage. It becomes apparent by setting W S (r’+ ,r’_)= 1 with μ s (r’+ ,r_) = 1 in Eq. (4), for any pair of points in the emission area of the source at the S plane. Thus, the energy units become irrelevant, and Eqs. (1a) and (2a) take the forms
And
Equations (5) realize the source-turned-off state of the setup. The source-turned-on state is established by setting Eq. (4) with the energy distribution and the spatial correlation properties of the physical source attached at the S plane. Equations (5) lead to a very important and novel interpretation of the source-turned-off state:
(i) The complete set of geometric modes are established with the same relative weight in the SM-stage volume by the stage configuration.
(ii) The arguments of
 relate each point r’A on the emission area of the S plane with any structured support on the M plane, specified by (ξ+ ,ξ_). So,
relate each point r’A on the emission area of the S plane with any structured support on the M plane, specified by (ξ+ ,ξ_). So,
 can be geometrically interpreted as cones in the SM-stage, with vertices at each emission point on the S plane and with the structured supports at the M plane as bases. Their specific geometry is determined by the modal expansion (5a) and spatially modulates the SM-stage.
can be geometrically interpreted as cones in the SM-stage, with vertices at each emission point on the S plane and with the structured supports at the M plane as bases. Their specific geometry is determined by the modal expansion (5a) and spatially modulates the SM-stage.
(iii) Equation (5a) points out that the cone value at its vertex r' A is determined by the contributions of all the pairs of points contained in the structured support centered at the cone vertex, symmetrically distributed around this vertex with separation vectors r’D. Each pair contributes with a specific mode, given by Eq. (3a), to the modal expansion of the cone.
(iv) The modal expansion (5b) overlaps the cones
 with vertices on all the emission points at the S plane and bases on the same structured support at the M plane, thus determining the prepared two-point correlation over this structured support. It means that each cone
with vertices on all the emission points at the S plane and bases on the same structured support at the M plane, thus determining the prepared two-point correlation over this structured support. It means that each cone
 describes the spatial or geometrical contribution of the structured support centered at a given point of the S plane to the preparation of the two-point correlation over any structured support on the M plane. For this reason,
describes the spatial or geometrical contribution of the structured support centered at a given point of the S plane to the preparation of the two-point correlation over any structured support on the M plane. For this reason,
 is called the correlation cone, Figure 1 (Castañeda, 2017 b) (Castañeda & Matteucci, 2017).
is called the correlation cone, Figure 1 (Castañeda, 2017 b) (Castañeda & Matteucci, 2017).
So, Eq. (4) and the analysis above specify the role of the physical source of waves and particles in the source-turned-on state. The energy distribution and the two-point correlation properties of the source cannot create more or different modes in the SM-stage. These source attributes can only select a subset of modes and change their relative weights, so that W S (r’+, r’_ ) plays the role of a modal filter.
High correlated and uniform sources select the complete set of modes with the same relative weight. In this case, the correlation cones provide the more elaborated geometric modulation of the SM-stage volume. The subset of modes selected by low correlated and/or non-uniform sources and their different relative weights simplify the geometric modulation of the stage. The simplest one is used by a single point source placed at any position r’A = r’0, so that
 and the correlation cones are given by
and the correlation cones are given by
Therefore, the prepared two-point correlation over any structured support at the M-plane becomes
Figure 2 illustrates the magnitudes of the correlation cone with vertex on r’ 0 =0 and basis centered at ξ, A =0 for (a) quantum particles and (b) classical waves.
Non-correlated extended sources are of special interest because they represent most the thermal emission sources of light or matter particles. They are described by w s (r’ + ,r’_)= s s (r' A )δ(r’ p ) for the points in the emission area of the source, so that

Figure 2 (a)-(b) Magnitudes of the correlation cones and (c)-(d) energy cones associated to a single point source at the S-plane in the SM-stage for (a), (c) individual quantum particles and (b), (d) classical waves. Vertical profiles in (a)-(b) describe the Lorentzian cross-section of the structured support centered on the optical axis at z = 100λ, while in (c)-(d) describe the Lorentzian cross-section of the illuminated area at z = 100λ.
describes the correlation cones with vertices at each emission point of the source, and
describes the prepared two-point correlation over any structured support at the M plane. The paraxial approach of Eq. (7b) in partially coherent optics is called the Van Cittert -Zernike theorem (Born & Wolf, 1993). Accordingly, the source-turned-on state reveals that (i) a set of correlation cones are selected and weighted at the input plane, (ii) their overlapping modulates geometrically the space in the SM-stage, thus producing the increase of the two-point correlation at the output plane.
An important feature of the prepared two-point correlation is that the effective size of the structured supports of correlation at the M plane is finite, and the biggest is the Lorentzian shaped support provided by the correlation cone associated to a single point source at the S-plane. The increase of the source size reduces the sizes of the structured supports, as shown in Figure 3 (a)-(b). This reduction is greater by non-correlated sources than by correlated sources in some extent, as illustrated in (c)-(d).

Figure 3 Comparison of the shapes and sizes of the structured supports of correlation centered at ξ A = 0 on the M plane. N is the number of emitting points of the corresponding linear source. The spacing of the set of points is a = λ/2, so that the arrays are under diffraction condition (Castañeda, 2017 a). The central maxima determine the effective area of the structured supports. (a) and (b) show that the size of the structured support diminishes as the number of points (i.e. the source size) increases. In (c) and (d), the decreasing of the structured support related to a given set of points is due to a reduction of the two-point correlation at the S-plane.
Now, let us analyze the pure geometrical (or energy independent) feature in the MD-stage for the energy measurement at the D-plane. Let us begin by regarding the source-turned-off state, in which the prepared two-point correlation in Eq. (5b) is the input to the modal expansion (2b). It means that the geometric modulation of space in the SM-stage induces the geometric modulation of the space in the MD-stage.
This causal connection between the geometric modulations of space in the two stages realizes the P & M scheme for interference and diffraction, with the following features:
(i) The modal expansion (2b) shows that the prepared two-point correlation described by Eq.(5b) is a modal filter that selects and weights a subset of the modes in the MD-stage, given by Eq. (3b).
(ii) The arguments of wMB(ξA;rA) relates each point ξA at the M plane to all points at the D plane. So, wMB(ξA;rA) can be geometrically interpreted as cones in the MD-stage, with vertices at each point rA on the M plane and with the detection area at the D plane as bases. The specific geometry of the cones is determined by the modal expansion (2b) and specify the spatial modulation of the MD-stage.
(iii) Equation (2b) points out that the cone value at its vertex % A is determined by the contributions of all the pair of points contained in the structured support centered at the cone vertex, symmetrically distributed around this vertex with separation vectors ξσ. Each pair contributes with a specific mode, given by Eq. (3b) to the modal expansion of the cone.
(iv) Equation (1b) overlaps all the cones wMB(ξA;rA) in the MD-stage, thus determining the spatial distribution of the energy to be measured, once the setup state changes to source-turned-on. It means that each cone wMB(ξA;rA) describes the contribution of the structured support centered at a given point of the M plane to the energy distribution to be measured at the D plane. For this reason, wMB(ξA;rA) is called the energy cone, Figure 1 (Castañeda, 2017 b) (Castañeda & Matteucci, 2017).
By using the Schwarz inequality as before, by the source-turned-on state, the prepared two-point correlation can be expressed as
where SΜ(ξ±) represents the energy distribution of the waves or particles arriving to the M plane, and

 denotes the complex degree of correlation at this plane, with
denotes the complex degree of correlation at this plane, with

 and similar mathematical properties to those of the complex degree of correlation at the S plane. Therefore, the prepared two-point correlation filters the modes of the expansion (2b) with basis on the energy distribution and/or the degree of correlation at the M plane. Figure 2 illustrates the Lorentzian shaped energy cones provided in the SM-stage by a point source placed on the optical axis at the S plane for (c) quantum particles and (d) classical waves. The vertical profiles describe the spatial distribution of the energy of the particles and waves arriving to the plane placed at z' = 100λ from the S plane.
and similar mathematical properties to those of the complex degree of correlation at the S plane. Therefore, the prepared two-point correlation filters the modes of the expansion (2b) with basis on the energy distribution and/or the degree of correlation at the M plane. Figure 2 illustrates the Lorentzian shaped energy cones provided in the SM-stage by a point source placed on the optical axis at the S plane for (c) quantum particles and (d) classical waves. The vertical profiles describe the spatial distribution of the energy of the particles and waves arriving to the plane placed at z' = 100λ from the S plane.
The source-turned-off state is realized in the MD-stage by setting S M (ξ±)=1, in such a way that W M (ξ + , ξ_)=μ Μ (ξ+, ξ_) holds and is determined by Eq. (5b). By replacing it in Eq. (2b), the geometry of the energy cones in the MD-setup is revealed, i.e.
For interpretation purposes, it is very useful to separate the component of the cone provided by the pairs of points (ξD
#Ο) enclosed in the structured support that determine the integration domain of Eq. (9), and the component provided by the center of the structured support (ξD=0) , i.e. the contribution associated to the single point in the support. It is performed by introducing the dimensionless function
 , with δ(ξD) the Dirac's delta, in the integral of Eq. (9) so that
, with δ(ξD) the Dirac's delta, in the integral of Eq. (9) so that
It follows
as the cone component provided by the single point at the support center. It is a real valued and positive definite function that describes a Lorentzian shaped cone. In addition,
with Re denoting the real part, by regarding

 . It leads to
. It leads to
with
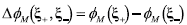 the phase difference of the transmission function of the M plane at the pair of points ζ±. It is a real valued function that takes on positive and negative values and describes a cone whose geometry has a spatially oscillating modulation with a Lorentzian envelope.
the phase difference of the transmission function of the M plane at the pair of points ζ±. It is a real valued function that takes on positive and negative values and describes a cone whose geometry has a spatially oscillating modulation with a Lorentzian envelope.
An important difference between the cones
 and
and
 is appreciable in Eqs. (11). The first one is defined by a single mode which is independent from the prepared degree of correlation at the M plane. It only depends on the MD-stage configuration and its geometry is the same for all the single points of the M plane with non-null absorbance. In contrast, the second one is determined by a modal expansion weighted by the prepared degree of correlation, and therefore it depends on the two setup stages. As a consequence,
is appreciable in Eqs. (11). The first one is defined by a single mode which is independent from the prepared degree of correlation at the M plane. It only depends on the MD-stage configuration and its geometry is the same for all the single points of the M plane with non-null absorbance. In contrast, the second one is determined by a modal expansion weighted by the prepared degree of correlation, and therefore it depends on the two setup stages. As a consequence,
 if the prepared degree of correlation nullifies.
if the prepared degree of correlation nullifies.
Accordingly, only the cone
 is actually induced by the preparation SM-stage and its role in the cone overlapping established in Eq. (10) is to modulate the cones
is actually induced by the preparation SM-stage and its role in the cone overlapping established in Eq. (10) is to modulate the cones
 , thus determining the complete geometry of the cone
, thus determining the complete geometry of the cone
 that characterizes the space modulation of the MD-stage. For this reason, the cone
that characterizes the space modulation of the MD-stage. For this reason, the cone
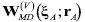 is called the modulating cone (Castañeda, 2017 b) (Castañeda & Matteucci, 2017).
is called the modulating cone (Castañeda, 2017 b) (Castañeda & Matteucci, 2017).
The change of state to source-turned-on is realized by setting the prepared energy distribution at the M plane,
 , in Eq. (8). According to Eqs. (11), this energy distributes on the cones in the volume of the MD-stage as follows:
, in Eq. (8). According to Eqs. (11), this energy distributes on the cones in the volume of the MD-stage as follows:
and
respectively. Thus, the spatial distribution of the energy measured at the D plane can be expressed as

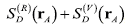 , with
, with
And
the individual contributions of the cone components in Eqs. (12), obtained from Eqs. (1b) and (10). Both energy terms are real valued but
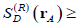 and it is independent from the prepared two-point correlation at the M plane, while
and it is independent from the prepared two-point correlation at the M plane, while
 takes on positive and negative values and depends closely on the prepared two-point correlation. In fact,
takes on positive and negative values and depends closely on the prepared two-point correlation. In fact,
 and therefore
and therefore
 if the prepared degree of correlation nullifies. In addition, the energy distribution in the MD-stage should be conservative. Specifically,
if the prepared degree of correlation nullifies. In addition, the energy distribution in the MD-stage should be conservative. Specifically,
With
Then, it follows
and
which implies,
The above analysis lead to the following conclusions:
(i) The coefficient S
M
(ξΑ) | t
M
(ξA) |2 in Eq. (12a) represents the energy of the wave disturbance or the particle that crosses the M plane at the vertex of the cone
 . This energy is a physical observable and distributes over such cone, thus being recorded by the detector still if there are no modulating cones. For this reason,
. This energy is a physical observable and distributes over such cone, thus being recorded by the detector still if there are no modulating cones. For this reason,
 is called the real cone. It is therefore theoretically reasonable to postulate the presence of a point emitter at the real cone vertex that emits the energy S
M
(ξΑ) | t
M
(ξA) |2 when the wave disturbance or the particle crosses such point. Such emitter is called the real point emitter (Castañeda, 2017 b) (Castañeda & Matteucci, 2017), and its contribution
is called the real cone. It is therefore theoretically reasonable to postulate the presence of a point emitter at the real cone vertex that emits the energy S
M
(ξΑ) | t
M
(ξA) |2 when the wave disturbance or the particle crosses such point. Such emitter is called the real point emitter (Castañeda, 2017 b) (Castañeda & Matteucci, 2017), and its contribution
 at the D plane is the emitted energy component of the measured energy.
at the D plane is the emitted energy component of the measured energy.
The energy
 is not a physical observable but has the important role to modulate spatially the emitted energy
is not a physical observable but has the important role to modulate spatially the emitted energy
 thus producing the measured energy distribution
thus producing the measured energy distribution
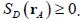 . It means that
. It means that
 . It is worth noting that the modulating energy
. It is worth noting that the modulating energy
 is essentially provided by the experimental setup. Indeed, it depends on the prepared degree of correlation at the M plane and its modes are determined by the MD-stage configuration. In addition, the coefficient
is essentially provided by the experimental setup. Indeed, it depends on the prepared degree of correlation at the M plane and its modes are determined by the MD-stage configuration. In addition, the coefficient
 in Eq. (13b) is introduced by the mathematical condition named Schwarz inequality and only assures the achievement of the requirement S
D
(rA ) ≥ 0. Indeed, if the experiment preparation provides high correlation and a uniform energy distribution at the M plane, then
in Eq. (13b) is introduced by the mathematical condition named Schwarz inequality and only assures the achievement of the requirement S
D
(rA ) ≥ 0. Indeed, if the experiment preparation provides high correlation and a uniform energy distribution at the M plane, then
 . Only under this condition
. Only under this condition
 holds at some points rA on the D plane, in accordance with the experimental observation of destructive interference. Therefore, the coefficient
holds at some points rA on the D plane, in accordance with the experimental observation of destructive interference. Therefore, the coefficient
 assures the achievement of
assures the achievement of
 at those points under such condition.
at those points under such condition.
The conclusions above lead to the following novel interpretation for the expression
It means that the measured energy distribution results from the spatial modulation of the emitted energy by the energy contributed by the experimental setup. Therefore, the modulating energy plays the role of the potential energy in the dynamical energy equation that specifies the total energy S D (rA ) of the classical wave disturbance or quantum particle that arrives to each point of the detector, in the source-turned-on sate of the setup.
In other words, Eq. (14) represents the global interaction of the emitted waves or particles with the setup, and points out that the spatial distribution of the measured energy, named interference or diffraction pattern, is a direct result of such interaction.
Consequently, in the source-turned-on state the modulating cone
 plays the role of a potential, whose name of geometric potential is clearly justified by the analysis above. It is theoretically reasonable to postulate the presence of a point emitter at the modulating cone vertex that emits the correlation energies
plays the role of a potential, whose name of geometric potential is clearly justified by the analysis above. It is theoretically reasonable to postulate the presence of a point emitter at the modulating cone vertex that emits the correlation energies
 which distributes over the modes of the expansion (12b), thus configuring the geometric potential in the volume of the MD-stage. This emitter is called the virtual point emitter, because of the mathematical properties of the geometric potential discussed above.
which distributes over the modes of the expansion (12b), thus configuring the geometric potential in the volume of the MD-stage. This emitter is called the virtual point emitter, because of the mathematical properties of the geometric potential discussed above.
Now, a unique physical description of interference and diffraction can be formulated for classical waves and quantum particles, by regarding two accessible states for the two-stage experimental setup in the P & M scheme. Basically, it regards that the setup configuration establishes a geometric modulation in the space with the physical ability to affect the movement of waves and particles in the setup, thus producing the interference and diffraction patterns.
More specifically, once the setup is configured in the source-turned-off state, the correlation cones spatially modulate the preparation stage thus determining the prepared complex degree of correlation on the mask plane. In addition, real cones are established in the measurement stage from the mask points at which wave disturbances or particles can cross the mask after the state change of the setup. The prepared degree of correlation induces modulating cones in the measurement stage that overlap the real cones modulating them geometrically. When the setup state changes to source-turned-on, local events of emission, mask-crossing and detection of wave disturbances or particles take place in the device. It is irrelevant that several of such events occur simultaneously as in case of classical waves, or sequentially as in case of individual quantum particles, because the description of the pattern formation at the detector plane is independent of this feature.
After an emission event, the emitted wave or particle arrives to a point in the prepared structured support of correlation of the cone with vertex on the emission point. Wave and particle arrivals are characterized by local energy amounts at the arrival point on the M plane. After crossing the mask at this point, the wave or the particle should move through the geometric potential induced in the measurement stage by the prepared two-point correlation. Consequently, its energy spatially changes, thus indicating that the wave disturbance or the particle is driven along preferential directions by the geometric potential up to its detection.
This physical and geometrical description is quite different to the standard one, because it does not base on the wave superposition and not requires the wave-particle duality, the self-interference or the wave collapse hypotheses.
The new principle
The above description of interference and diffraction can be synthetized in a physical principle with the corresponding law. To this aim, let us consider the simplest basic interference experiment, i.e. the double pinhole experiment with classical waves or quantum particles, named the Young's experiment, Figure 4. It is sufficient to analyze the measurement MD-stage in order to synthesize the new principle and law by assuming a given two-point correlation W M (ξ +,ξ_), prepared at the M plane. The transmission function of the double pinhole mask fulfils the formula
with b the pinhole separation. The first line of Eq. (15) refers to the individual pinholes, characterized by the factor δ ( ξ
D
), while the second line refers to the correlated pair and include the two degrees of freedom in orientation of the separation vector. The cone
 that describes the geometric modulation of the space can be expressed as
that describes the geometric modulation of the space can be expressed as
It results from the overlapping of two real cones with vertices at the pinholes and one modulating cone with vertex at the midpoint between the pinholes, in the opaque segment of the mask.
In the source-turned-off state of the setup, the real cones take the Lorentzian shaped form
and the modulating cone has the cosine cross-section with Lorentzian envelope (Figure 4) given by
It is apparent in Eq. (16c) that the non-null spatial correlation of the two pinholes (|μΜ (b)\ > 0) is the requirement for the existence of the modulating cone, i.e. both pinholes must be included in the prepared structured support of correlation centered at the midpoint between them. This condition implies that the pinhole separation must be shorter than the size of the prepared structured support. Otherwise, the modulating cone disappears and the MD-stage contains only the real cones.
Once the setup state changes to source-turned-on, the factors s
M
(± b/2) and
 appear respectively in the real cone, Eq. (16b) and Figure 5 (a)-(b), and in the modulating cone, Eq. (16c), thus giving the geometric potential defined as and illustrated in Figure 5 (c)-(d). Consequently,
appear respectively in the real cone, Eq. (16b) and Figure 5 (a)-(b), and in the modulating cone, Eq. (16c), thus giving the geometric potential defined as and illustrated in Figure 5 (c)-(d). Consequently,
 in Eq. (16a) becomes the energy cone illustrated in Figure 5 (e)-(f).
in Eq. (16a) becomes the energy cone illustrated in Figure 5 (e)-(f).

Figure 4 Conceptual sketch of the Young interference experiment, according to the P & M scheme. r and v label the real and the virtual point emitters. Upper graph: the source-turned-off state (the real cones in the MD-stage are not shown). Bottom graph: the source-turned-on state.
The coefficient
 establishes that both pinholes must remain open during the movement of the wave and the particles from the source to the detector (S
M
(±b/2) > 0). It is a necessary but not sufficient requirement for the existence of the geometric potential, still in experiments with individual particles that cross only one of the pinholes at a time. If any of the pinholes is blocked, then the coefficient
establishes that both pinholes must remain open during the movement of the wave and the particles from the source to the detector (S
M
(±b/2) > 0). It is a necessary but not sufficient requirement for the existence of the geometric potential, still in experiments with individual particles that cross only one of the pinholes at a time. If any of the pinholes is blocked, then the coefficient
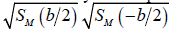 nullifies and the geometric potential disappears. Summarizing, the necessary and sufficient condition to establish the geometric potential in the MD-stage is that the two pinholes must be open and spatially correlated. It is realized by the definition of the two-point correlation in Eq. (8).
nullifies and the geometric potential disappears. Summarizing, the necessary and sufficient condition to establish the geometric potential in the MD-stage is that the two pinholes must be open and spatially correlated. It is realized by the definition of the two-point correlation in Eq. (8).
The necessary and sufficient condition for the geometric potential has an important physical implication. When both pinholes are open but non-correlated, so that μ Μ (ξ + ,ξ_)=0 for ξ D - b, then the energy cone in the stage results from the overlapping of the two real cones associated to the pinholes, without the modulation of the geometric potential, Figure 5 (a)-(b). It confirms that the geometric potential cannot be obtained by overlapping real cones. It can only be established by the setup configuration. Therefore, the interference modulation of the energy distribution in the MD-stage should be obtained by overlapping each real cone individually with the geometric potential, as shown in Figure 6.

Figure 5 Measurement MD-stage of the Young interference experiments with classical waves on the left column and with individual quantum particles on the right column. (a)-(b) Real cones, (c)-(d) geometric potential, and (e) and (f) modulated energy cones. the vertical and the horizontal axes are - 20λ ≤ x A ≤ 20λ and 0≤z≤10λ respectively. The pinhole separation is 10λ.

Figure 6 Energy cones in the measurement MD-stage associated to the individual interaction between the real point emitter in the pinhole at ξ Α =5λ and the virtual point emitter at ξ Α =0, in the Young interference depicted in Figure 5, with classical waves on the left column and with individual quantum particles on the right column. The vertical axes are - 20λ ≤ x A ≤ 20λ in (a)-(b) and -106λ≤x A ≤ 10 A in (c)-(d), and the horizontal axes are 0≤z≤10λ in (a)-(b) and 105A ≤ z ≤ 106λ in (c)-(d). Dotted lines in (a)-(b) delimit the region occupied by the non-modulated real cone associated to the real point emitter in Fig. 5 (a)-(b).
The analysis above indicates that the meaning of spatial coherence should be extended. In the standard formulation, it is described as an exclusive attribute of the physical objects (waves or particles). The new model relates two features to it: (i) the ability of the setup configuration to determine the set of geometric modes for the correlation cones, and (ii) the filtering ability of the source of waves and particles to select and to weight the subset of geometric modes that effectively conforms the correlation cones. It has been shown before that the preparation of the two-point correlation at the M-plane is the choice of a geometrical modulation, performed by the source correlation, among all the possible ones that can be provided by the setup. It means that the direct role of the source spatial coherence is restricted to the preparation stage.
The physical description in the last paragraph of the section before is confirmed by Figure 6 (a)-(b), i.e. the wave disturbance and the crossing particles by the pinhole at ξ Α = 5λ find, in the volume of the MD-stage, the geometric potential provided by the virtual point emitter at ξ Α = 0. Consequently, they must move through the spatial modulation established by such geometric potential. The upper region of the graphs with respect to the dotted lines illustrates the energy cones after a great enough number of crossing events. This is the region occupied by the corresponding non-modulated real cone in Figure 5 (a)-(b). The modulation of the bottom region is due to the geometric potential only.
At a far enough distance from the mask, the individual real cones fill the whole volume of the stage. Therefore, the corresponding modulated energy cone fills the whole volume too, as shown in Figure 6 (c)-(d). Because the geometric potential performs the same geometric modulation to the real cones associated to the both pinholes, the graphs (c)-(d) are the same for the energy coming for any of the pinholes. As a consequence, if the detection is realized in the far-field region, it is not possible to distinguish the energy distribution contributed by each of the pinholes. However, this indistinguishability is removed, still maintaining some spatial modulation, in the very near region to the M-plane as shown in the graphs (a)-(b). It also means that the interference modulation does not require the overlapping of the real cones.
Figures 5 and 6 evidence the meaning of the space scale metric and its relationship with the wave and particle wavelengths in the measurement MD-stage, i.e. similar shaped patterns essentially differing in scale, are obtained with classical waves that simultaneously illuminate the two pinholes and with individual quantum particles that crosses only one pinhole at a time.
This analysis clearly departs from the description based on the wave superposition, in which the (classical or quantum) wave contributions from the both pinholes constitute the necessary and sufficient cause of interference. The standard description precludes the occurrence of interference when only one of the two open pinholes contributes with wave disturbance or particle crossings. In case of interference with individual quantum particles, this requirement leads to the notion of self-interference of the particles in order to provide the required probability amplitudes at the both pinholes. Self-interference is also behind the interference with classical waves, because the disturbances at the two pinholes belongs to the same wave-front. In contrast the geometric interpretation does not require the self-interference notion, because in this framework interference is formed because of the spatial modulation of the real cones by the geometric potential, which forces the energy of the waves and the particles to be distributed on certain preferential regions of space.
The overlap of the individual modulated real cones gives the well-known interference patterns, recorded after a great enough number of detection events. Thus, the energy cone in the MD-stage can be expressed as
with
the individual modulated real cones by the geometric potential. From Eqs, (1b) and (17) it follows
as the energy distribution recorded by the detector at the M-plane, with
the energy distribution over the basis of each modulated energy cone. In addition,
is the energy distribution across the basis of each individual real cone, provided by the wave disturbance or the crossing particles at the corresponding pinhole, while
is the potential energy across the basis of the geometric potential cone provided by the stage configuration. This potential energy spatially modulates the energy provided by the individual real cones. It should be noted that:
(i) and
 but
but
 takes on positive and negative values. Therefore,
takes on positive and negative values. Therefore,
 holds for
holds for
 .
.
(ii) The energy distribution provided by the real cones is independent from the prepared two-point correlation, while the potential energy does. In other words, the preparation of the two-point correlation in the SM-stage determines the potential energy distribution at the D-plane.
(iii) Because
 , and
, and

 , then
, then
 it means that the distribution of the energy in each individual modulated real cone is conservative.
it means that the distribution of the energy in each individual modulated real cone is conservative.
The analysis above leads to the following conclusions:
(i) Only three point emitters, two real and one virtual, are required to describe the energy measurement in the MD-stage of the double pinhole Young interference. These point emitters are placed at different positions on the M-plane, i.e. the real point emitters are in the pinholes and the virtual point emitter is at the opaque segment of the mask between de pinholes.
(ii) Equation (18b) can be interpreted as the energy at the D-plane due to the interaction, at the M-plane, between each real point emitter that characterizes the classical waves or the quantum particles, and the virtual point emitter that characterizes the experimental setup. These interactions are separate and their effects are additive as expressed in Eq. (18a).
(iii) Because the overlap of the real cones cannot produce interference modulation, the interaction between the real point emitters is forbidden. This feature is an additional departure of the geometric interpretation from the standard models based on the wave superposition.
The general statement that interference is the result of the separate interaction between individual real point emitters and the virtual point emitters constitute the principle of interference in the framework of the geometrical interpretation. It can be equivalently stated as follows: interference results from the interaction between the emitted waves or particles with the geometric potential determined by the setup configuration.
Although the geometric modulation of space in both the SM- and the MD-stages, arranged in a P & M scheme, occurs in the source-turned-off state, interference is a physical phenomenon occurred in the source-turned-on state. Therefore, Eq. (18b) constitutes the general law of interference in this framework.
From interference to diffraction
In the framework of the geometric interpretation, the interaction principle synthetized from the double pinhole interference is the general principle for interference and diffraction. In the following, grating interference and diffraction are discussed from this point of view.
It has been proved in classical optics that a P & M schemed setup with space scale metric λ and a regular array, with spacing b and length L, of real point emitters of waves attached at the M-plane produces interference if b > λ and diffraction if b < λ and L > λ (Castañeda, 214, 2017 a). Now, the validity of this result is extended for interference and diffraction with quantum particles.
To this aim, let us assume, for simplicity and without loss of generality, a similarly configured setup with a pinhole grating at the M plane with a linear array of 2 M + 1 pinholes (M a positive integer). In the source-turned-on state, the pinhole grating determines a corresponding array of real point emitters, and the setup configuration induces a set of 0 ≤ N ≤ 4M -1 virtual point emitters distributed along the segment of pinholes, whose specific number and strength depend on the shape and size of the prepared degree of correlation. They are placed at the positions ξ Α = ( m + n ) b¡ 2 which are the midpoints between pairs of pinholes with separations ξ Β =(m - n)b, inscribed in the prepared structured supports centered at the ξ Α positions.
The set of real point emitters contributes the energy distribution
at the D plane, while the potential energy distribution there due to the set of virtual point emitters is given by
so that the energy distribution resulting from the interaction between the sets of real and virtual point emitters is given by
 . It is illustrated in Figure 7 for a great enough number of emission events of an array of 21 identical real point emitters (M = 10), of length L = 10λ and spacing b = λ/2, under the prepared correlation degree μ
Μ
(mb,nb) = 1 that produces the maximal number of virtual point emitters, i.e. 39. Accordingly, diffraction should occur in the measurement MD-stage when the setup is in the source-turned-on state.
. It is illustrated in Figure 7 for a great enough number of emission events of an array of 21 identical real point emitters (M = 10), of length L = 10λ and spacing b = λ/2, under the prepared correlation degree μ
Μ
(mb,nb) = 1 that produces the maximal number of virtual point emitters, i.e. 39. Accordingly, diffraction should occur in the measurement MD-stage when the setup is in the source-turned-on state.

Figure 7 Diffraction in the measurement MD-stage resulting from the interaction between 39 virtual point emitters associated to 21 high correlated pinholes and the corresponding individual real point emitters, for single quantum particles on the left column and for classical waves on the right column. Vertical axes are corresponding to Χ A (μm) and the horizontal axes to z (μm) Energy profiles are shown at the corresponding vertical axes. Symbols + and - denote the positive and negative semi-axis. Images were enhanced on the left part (left column) and on the right part (right column) to appreciate details. Delta-like peaks were truncated for presentation purposes.
It is remarkable that, in spite of the discreteness of the set of real point emitters, non-paraxial slit diffraction patterns are formed from relative short distances to the far-field by both classical waves (Castañeda, 2014 a, b) (Castañeda, 2017 a) and individual quantum particles (Castañeda, et al., 2016 a, b) (Castañeda & Matteucci, 2017), in good accordance with reported experimental results in light optics (Born & Wolf, 1993) and electron optics (Matteucci, 1990) (Matteucci, et al., 2013). As expected, the graphs are similarly shaped but different in scale. So, the diffraction condition proved for classical waves is also fulfilled by individual quantum particles. It leads to the conclusion that, in the framework of the proposed geometric model, diffraction occurs in the source-turned-on state of the setups, provided that the discrete set of radiant point emitters fulfils the condition b < λ and L > λ, with λ the setup space scale metric, b the array spacing and L the array length, independently if waves or particles move in it.
It should be remarked that discreteness in this context is not a consequence of a sampling procedure for numerical calculations, but a physical condition for the experimental realization of diffraction. Indeed, it has been proved that any linear array of real point emitters with L < λ/10 behaves like a single real point emitter independently from the number of point emitters, the prepared two-point correlation and the sampling procedure to perform the numerical predictions (Castañeda, 2017 a). It is due to the fact that the setup cannot provide a geometric potential capable to modulate the real cones of such array. This conclusion contrasts with the standard notion that only continuous (classical or quantum) wave-fronts can produce or predict the buildup of diffraction patterns. Continuous arrays of real point emitters seem to be redundant sets for diffraction.
In many cases, the attached mask at the M plane can gather points in separate sets, with separations longer than the space scale metric, but each one with b < λ and L > λ. These sets can be inscribed, partially or completely, in the prepared two-point correlation. So, in the source-turned-on state the setup provides a geometric potential with:
(i) An interference modulation component for the interactions between the real point emitters of any set with the virtual point emitters that associate this set with the other sets.
(ii) A diffraction modulation component for the interactions between the real point emitters of a set with the virtual point emitters associated to pairs with the same set.
(iii) The diffraction component of the geometric potential modulates the interference component.
Let us illustrate these features with the simplest experimental situation, i.e. the double slit experiment, whose energy cones in the MD-stage are shown in Figure 8. The slits of the mask at the M plane determine two co-linear arrays of 11 real point emitters each one, with b = λ/2 and L = 5λ. The arrays separation is a = 10λ. A Gaussian two-point correlation is prepared, whose standard deviation σ Μ determines the correlation length (i.e. the size of the structured supports) at the M plane. So, the setup induces 0<N L <19 virtual point emitters within each slit, and 0≤N a ≤21 virtual point emitters at the opaque region between the slits, depending on the value of σΜ. The distributions of the discrete sets of real point emitters in the slits are represented by the energy profiles at z = 0 in all graphs of Figure 8. The maximal number of virtual point emitters, N L + N a = 40, are induced in graphs (a)-(b) for classical waves. The real point emitters of both slits interact with this set of virtual point emitters, so that the wave energy distributes over the geometric potential in the MD-stage as shown in (a) near the M plane and (b) in the far-field, after a great enough number of crossing events through the slits. The geometric potential modulates the individual real cones before they are completely overlapped, in the region near the M plane, and produces a high contrasted interference pattern modulated by diffraction in the far-field.
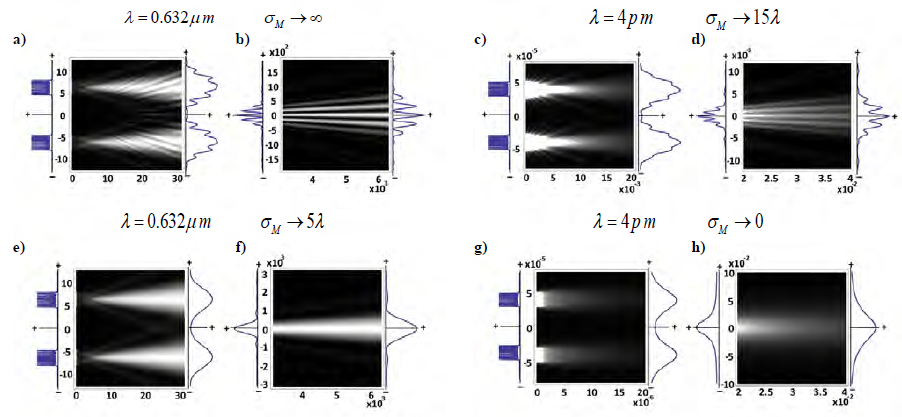
Figure 8 Energy cones in the MD-stage of a double slit experiment with Gaussian two-point correlation prepared at the M-plane, with correlation length σ Μ . The setup is configured for classical waves (λ = 0.632μm) and for single quantum particles (λ = 4pm). x A (μm) and z (μm) are the vertical and the horizontal axes, respectively. Energy profiles are shown at the corresponding vertical axes. Symbols + and -denote the positive and negative semi-axis. Graphs on the left column describe the energy cones near the slit mask, while those on the right column denotes the energy cones in the far-field. Images are enhanced for presentation purposes.
The set of virtual point emitters diminishes in (c)-(d) to 19 < N L + N a < 40 for single quantum particles, by reducing the correlation length in such a way that the structured supports centered at ach slit covers them completely but the structured support centered at the midpoint between the two slits cover them partially. Consequently, the diffraction component of the geometric potential is maintained but the contrast of the interference component is reduced. It means that the real point emitters realize the interaction with the maximal set of virtual point emitters within each slit, but with a smaller set of virtual point emitters between the slits.
The correlation length is reduced to the slit width in (e)-(f) for classical waves, so that N = N L = 19. It means that the interference component of the geometric potential is filtered out and only the diffraction component remains. Therefore, the sets of real point emitter of each slit interact only with the virtual point emitters within the slit. The energy cones near the M plane as well as in the far field do not exhibit interference modulation, so that the energy distribution of the wave at the D plane in the far-field reproduces the diffraction pattern associated to each individual slit.
Finally, the correlation length becomes σ Μ << b in (g)-(h) for single quantum particles, so that N = 0. Both components of the geometric potential are filtered out and there are no interactions. So, the overlapping of the Lorentzian shaped real cones gives Lorentzian shaped energy cones too.
The results above point out a worthy feature of the structured supports of correlation: each virtual point emitter interacts only with the pairs of radiant point emitters inscribed in its structured support. Accordingly, there is no interaction between the real and the virtual point emitters placed at the same point.
The complete map of interactions can be determined by using the spectrum of classes of point emitters, a novel and very effective tool reported in (Castañeda, 2016) for classical waves and (Castañeda & Matteucci, 2017) for quantum particles.
Non-paraxial Talbot carpets
They are interference patterns that repeat at given axial positions in the region near the M plane in the MD-stage (Wen, et al., 2013). They are produced when b >> λ, so that the geometric potential contains mainly high spatial frequency modes. Consequently, the interference patterns will be highly contrasted and sharply localized along the z-axis, and their main maxima will be extremely narrow.
Figure 9 illustrates similar shaped non-paraxial Talbot carpets with light waves and single quantum particles. It is remarkable that the vertical patterns with the highest main maxima are not equidistant along the propagation axis nor have the same spacing. It is due to the non-linear argument of the geometric potential modes. This non-paraxial feature, predicted by the geometric model, is crucial in technological applications, in which the stringent tolerances for the substrate positioning is definitive to build molecular nano-wires. Specifically, by using molecules, a real time adjustment of the thin film patterning is not feasible so that a precise design of the experimental setup is strictly needed. In this sense, the far-field paraxial approach is not a suitable methodology for the calculation of Talbot carpets with single particle interference, required by technological developments.

Figure 9 Talbot carpets with classical waves (left column) and individual quantum particles (right column). The prepared correlation degree is equal to one. Five real point emitters with spacing of 104 λ are considered in (a)-(b), and 21 emitters with spacing 105 λ are considered in (c)-(d). x A (μm) and z (μm) are the vertical and the horizontal axes, respectively, with -103λ ≤x A ≤ 103λ and 2χ10 6 λ≤z≤4χ10 6 λ in (a)-(b) and with -2χ104 λ≤χ Α ≤2χ104λ and 109λ ≤ z ≤ 1.8 χ 109 λ in (c)-(d).
Reported experimental evidences
Remarkable experimental evidences of the validity of the geometric model were recently reported (Castañeda, et al., 2016 a, b). Indeed, it provided accurate predictions of experimental interference patterns performed by other authors, with single electrons (Matteucci, et al., 2013), single molecules of Phthalocyanine (PcH2) and its derivative (F24PcH2) (Juffmann, et al., 2012), and Fullerene C60 (Nairz, et al., 2003). These beautiful experiments open new basic and practical perspectives, not only to test the wave nature of massive particles, but also to develop technological applications regarding the scaling down of molecule based devices as transistors and diodes used in organic electronics (Cappelli, et al., 2014).
The validity of the geometric model has been evidenced in case of interference and diffraction of electromagnetic waves too (Castañeda, 2014 a). Furthermore, two-dimensional arrays of real and virtual point emitters have been used for modelling diffraction and interference with light wave-fronts (Castañeda, 2014 b). Such arrays can be decomposed in a finite number of additive one-dimensional distributions, so that the geometric model can be applied with mathematical simplicity and without lack of generality.
Conclusion and summary
The physical description of interference and diffraction with classical waves and quantum particles has been discussed in the framework of a geometric model based on a unique principle and the same general law. The principle is the interaction between real point emitters that characterize the waves and particles moving in the setup, and the virtual point emitters that characterize the setup. It is quite different from the wave superposition, the fundamental notion of the standard description, not only in form but also in meaning. It has been proved, for instance, that the overlapping of real cones, which is the geometrical simile of the wave superposition, cannot produce the spatial distribution of energy called interference.
The fundamental features of the principle were discussed in detail, and the corresponding general law of interference was established by regarding that any interference or diffraction setup is configured in a P & M (preparation-measurement) scheme and has two accessible states named the source-turned-off and the source-turned-on states, determined by the operation of the source of waves or particles. In this context, the emission, mask crossing and detection events of the wave or particle energy are assumed as local events.
In addition, in the source-turned-off state the setup configuration provides a geometric modulation of the space by determining a set of geometric modes in the setup volume. Once the state changes to source-turned-on, a subset of specific modes is selected and weighted to configure correlation cones in the preparation SM-stage as well as cones of geometric potential in the measurement MD-stage. Consequently, pairs of points included in the structured supports of correlation (i.e. the bases of the correlation cones) at the mask plane become correlated in some extent and, because of this, such points become connected to specific modes of the geometric potential in the MD-stage.
The wave disturbance or the individual particle that arrives to a crossing point of the mask in a given structured support is characterized by the real point emitter placed at such point, which individually interacts with the virtual point emitter at the center of the structured support. Consequently, the wave disturbance or the single particle must move along the preferential directions determined by the corresponding geometric potential in the MD-stage, so that its energy at the detector becomes affected by the potential energy provided by the geometric potential.
It is expressed by the new general law for this interaction, which is an energy equation that involves the energy of the wave or the single particle and the potential energy provided by the setup. This law describes the energy distribution of interference and diffraction patterns depending on the distribution of the real point emitters at the mask plane.
The P & M scheme is therefore realized as the preparation of two-point correlation and the corresponding geometric potential, and the measurement of energy distributions.
As a very important consequence, the standard explanations of quantum interference and diffraction based on the wave-particle duality, self-interference and wave collapse are irrelevant in the framework of the geometric model, thus solving the mystery in the heart of quantum mechanics.
It is remarkable that the geometric model is completely causal and deterministic. Therefore, a subject to be analyzed in next papers concern the effects of the statistical features of the emission, the crossing and the detection events on this model.
Finally, the geometric model has been validated by its accurate prediction of interference and diffraction patterns with light (i.e. scalar optical fields) and electromagnetic waves (i.e. by including polarization states), single electrons and different types of single molecules.