Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introducción
El estudio de las llamadas nanoestructuras magnéticas suscita gran interés debido a sus propiedades físicas, entre las cuales se destacan los bajos puntos de fusión, la fotoluminiscencia debida a efectos cuánticos, y el superparamagnetismo en algunos materiales como el hierro (Fe), el cobalto (Co) y el níquel (Ni), y a sus diversas aplicaciones tecnológicas (Lu, et al., 2004; Gupta, et al., 2005; Sun, 2000; Cowburn, et al., 1999; Dormann, et al., 2007; Landeros, et al., 2009; Cisternas & Vogel, 2015), por ejemplo, los dispositivos de alta frecuencia, los filtros de información, las guías de onda, los cabezales de lectura en discos duros, las memorias magnéticas de acceso aleatorio (magnetoresistive random-access memory, MRAM), las MRAM de torsión de espín, y los osciladores de torsión de espín, entre otros (Philip, et al., 2008; Philip, et al., 2003).
Las propiedades magnéticas de nanoestructuras ferro-magnéticas como las películas delgadas, los nanohilos, y los nanotubos, entre otras, se han estudiado exhaustivamente tanto de forma experimental (Nielsch, et al., 2005; Schellekens, et al., 2013) como teórica (D Albuquerque & Castro, et al., 2002; García del Muro & Solans, 1997; Suarez O. J., et al., 2009; Suarez, et al., 2012). Su estudio teórico generalmente se ha abordado a partir del régimen de temperatura. A temperatura cero la dinámica de la magnetización se ha investigada mediante el uso de las ecuaciones dinámicas de Landau-Lifshitz (LL) y Landau-Lifshitz-Gilbert (LLG) (Landau & Lifshitz, 1935; Mayergoyz, et aí, 2009). En el caso de la temperatura finita, la dinámica magnética se ha modelado mediante el uso de la ecuación de Landau-Lifshitz-Bloch (LLB) (Garanin, 1991; Garanin, 1997), con resultados confiables en los fenómenos que se presentan a distintas temperaturas y escalas de tiempo ultrarrápidas. Por ejemplo, el método se ha convertido en una herramienta indispensable para la caracterización de la demagnetización ultrarrápida inducida por láser (Sultan, et al., 2012), el movimiento de la pared de dominio impulsado térmicamente a través del efecto espín-Seebeck (Hinzke & Nowak, 2011), el efecto de torsión de giro a temperaturas elevadas (Haney & Stiles, 2009; Schieback, et al., 2009), la grabación magnética asistida por calor (McDaniel, 2012), la dinámica ultrarrápida en materiales ferrimagnéticos (Atxitia, et al., 2012; Suarez, et al, 2015), y el caos determinista en partículas magnéticas (Suarez, et al., 2017).
En el área de la demagnetización ultrarrápida inducida por láser, se ha demostrado que la ecuación LLB describe adecuadamente la dinámica en materiales como el Ni y el gadolinio (Gd). La característica principal de la ecuación LLB, que la hace idónea para la dinámica de magnetización ultrarrápida, es que presenta un término de relajación longitudinal que proviene de la fuerte interacción magnónfonón.
Uno de los efectos más estudiados para entender la dinámica de magnetización de partículas magnéticas ha sido la resonancia ferromagnética (RFM). Esta técnica se ha utilizado para medir parámetros de disipación, la relación giromagnética y la constante de anisotropía en películas delgadas (Farle, 1998; Ellis, et al., 2012) y en sistemas de válvula de espín, compuestas de iridio-manganeso (IrMn), Co, rutenio (Ru) y níquel-hierro (NiFe). Los modelos teóricos se han elaborado con la aproximación de temperatura cero mediante las ecuaciones LL y LLG. En estos estudios se ha observado que la dependencia angular del campo de resonancia muestra un acoplamiento antiferromagnético y campos de anisotropía unidireccionales, lo cual hace que el sistema presente un comportamiento que se ajusta casi a la perfección, en comparación con los resultados experimentales (Tarazona-Coronel, et al, 2014). Asimismo, en múltiples estudios teóricos realizados a temperatura cero se han contrastado sus modelos con los experimentales, con muy buenos resultados (Curiale, 2008; Anaya-Calvo, 2013; Forzani, et al, 2016).
En estudios más completos se han analizado los efectos de la temperatura finita. Por ejemplo, en la caracterización de películas delgadas de Ni50Fe50 depositadas sobre substratos de Si(001), se observó mediante el uso de la RFM que el campo de resonancia como función del ángulo del campo en el plano exhibe simetría uniaxial en todas las muestras, con un ligero corrimiento hacia valores menores a medida que disminuye la temperatura. Este comportamiento está asociado con las variaciones térmicas de la magnetización en el plano, lo que a su vez induce una disminución en la anisotropía de superficie en el sistema (Díaz de Sihues, et al., 2006). En estudios teóricos recientes también se han reportado los efectos de la temperatura en la resonancia ferromagnética. Empleando la ecuación LLB, los autores determinaron el espectro de absorción como función de la temperatura en una partícula magnética de material hierro-platino (FePt) y encontraron que la frecuencia de resonancia y el campo aplicado presentaban un corrimiento hacia valores menores de frecuencia con el aumento de la temperatura (Ostler & Ellis, 2014).
En este trabajo se hizo un estudio teórico sistemático de la resonancia de partículas magnéticas de diferentes materiales (FePt, Co y Ni) a temperatura finita y en presencia de un campo magnético externo. Se escogieron dichos materiales porque se conocen todos los parámetros que se requieren para la modelación bajo la aproximación de campo medio. Son muy pocos los estudios analíticos reportados en las bases de datos sobre nanoestructuras magnéticas en los que se consideran las variaciones de temperatura; ello nos motivó a llevar a cabo diversos estudios en esta línea de trabajo, la cual es un nicho importante de investigación.
El documento está organizado de la siguiente manera: en una primera sección se presenta el modelo teórico, en la siguiente se muestran y analizan los resultados obtenidos y en la última se presentan las conclusiones.
Modelo teórico
Se estudió una partícula magnética anisotrópica asumida como un monodominio, a temperatura finita en presencia de un campo magnético aplicado con dos componentes: una componente constante, H0, y una componente dependiente del tiempo, (h(t). La evolución temporal del vector de magnetización a temperatura finita se modeló mediante la ecuación de Landau-Lifshitz-Bloch (LLB):
donde m representa el vector de magnetización normalizado (m = M/M s ); M s es la magnetización de saturación de la partícula a temperatura cero absoluto; αӏӏ y α⊥ son los parámetros de disipación longitudinal y perpendicular, respectivamente; ү representa la relación de radio giromagnética de un electrón libre, y H eff representa el campo magnético efectivo del sistema. Este campo contiene todas las contribuciones de campo que sean consideradas en un sistema particular de estudio.
En este caso, el campo efectivo utilizado se expresa de la siguiente forma:
donde H Ap representa el campo magnético aplicado, y H AN es el campo de anisotropía definido de la forma:
El último término en la ecuación (2) es un campo de temperatura, el cual siempre se encuentra presente en el campo efectivo debido a que es un término que aparece en la deducción de la ecuación LLB. En las ecuaciones (2) y (3) m
e
(T) es la magnetización de equilibrio, y
y
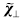son las susceptibilidades magnéticas paralela y perpendicular, las cuales son funciones de la temperatura. Los parámetros
y m
e
se toman desde la aproximación de campo medio. La magnetización de equilibrio se obtiene a partir de la ley de Curie-Weiss:
, donde ( es el momento magnético atomístico, J0 la intensidad del campo de intercambio, y ( = 1/k
B
T siendo k
B
la constante de Boltzmann (Garanin, 1997).
La función B(y) = coth (y) - 1/y representa la función de Langiven, la cual describe la magnetización para materiales como el Ni y FePt, mientras que para Co, la magnetización se modela con la función de Brillouin: B (y)
con valor de espín S=1/2 (Moreno, et al., 2016).
Los parámetros de disipación longitudinal y perpendicular dados en la ecuación (1) son funciones de la temperatura, que en la aproximación de campo medio se definen como:
donde α es el coeficiente de disipación a temperatura cero. Las susceptibilidades magnéticas paralela y perpendicular son dadas por las expresiones:
donde K(T) = K m e n (T), siendo K 0 = K(T = 0) la constante de anisotropía a temperatura cero y n un exponente de escala específico para cada material.
Se hizo aquí un estudio comparativo de la resonancia ferromagnética a temperatura finita en tres materiales: FePt, Co y Ni. En la Tabla 1 se presentan los valores de los parámetros utilizados para las simulaciones, así como las correspondientes expresiones para el cálculo de la intensidad del campo de intercambio (J0) en la aproximación de campo medio.
Tabla 1 Parámetros utilizados para la caracterización del sistema (Anaya-Calvo, 2013; Ostler & Ellis, 2014; Garanin, 1991).
| Material | Parametros | |||||
|---|---|---|---|---|---|---|
| Ms (J/Tm3) | Tc (K) | K0 (J/ m3) | μ (Am2) | η | J0 | |
| FePt | 1,05 × 106 | 660 | 8,2 × 106 | 3,23 μB | 2,1 | 3kBTc |
| Co | 1,42 × 106 | 1360 | 5,3 × 105 | 1,72 μB | 3 | kBTc |
| Ni | 4,8 × 105 | 630 | 5,3 × 103 | 0,61 μB | 3 | 3kBTc |
Análisis y resultados
Se estudió una partícula magnética con anisotropía uniaxial a lo largo del eje z; el campo externo aplicado tuvo una componente constante, Hz=H0||z, aplicada a lo largo del eje fácil y una componente armónica dependiente del tiempo, (h(t), aplicada de forma perpendicular a este con la condición |δh(t)| << |Hz|. Cerca de la resonancia, el campo (h(t) suministra energía suficiente al sistema como para compensar las pérdidas de energía asociadas con la interacción de los momentos magnéticos y el medio circundante, lo cual mantiene la magnetización en un estado dinámico. Dada la excitación del campo dependiente del tiempo, la magnetización puede escribirse como M = M0 + (m, donde M0=M0m representa la magnetización de equilibrio y 5m representa la parte dinámica de la magnetización, con la condición |5m| << |M0|.
Empleando la ecuación LLB, se determinó la evolución temporal del vector de perturbación 5m, el cual se escribe finalmente en forma matricial como
, donde
es un tensor en variable compleja llamado "tensor de susceptibilidad magnética", el cual es dado como
donde (
0 es la permeabilidad magnética del vacío, y A es una matriz 2 x 2 cuyas componentes están dadas por:
donde
, siendo Ω0 la frecuencia natural del sistema. La parte imaginaria de una componente del tensor de susceptibilidad magnética brinda información sobre la absorción energética que presenta el sistema. La componente x de dicho tensor, en nuestro caso, viene dada por la expresión:
donde
.
En las Figuras 1 y 2 se presentan gráficos de la componente x de la parte imaginaria del tensor de susceptibilidad magnética como función del campo constante Hz y la frecuencia Ω, respectivamente, para los materiales A) FePt, b) Co y c) Ni, a diferentes temperaturas. En los diferentes materiales la resonancia se obtiene para diferentes valores del campo aplicado Hz y la frecuencia del campo dependiente del tiempo.
Figura 1 Componente x de la parte imaginaria del tensor de susceptibilidad magnética como función del campo aplicado Hz para diferentes temperaturas. Las figuras se realizaron para: (a) FePt a 600 GHz, (b) Co a 30GHz y (c) Ni a 3 GHz.
Figura 2 Componente x de la parte imaginaria del tensor de susceptibilidad magnética como función de la frecuencia para diferentes temperaturas. Las figuras se realizaron para un campo aplicado fijo de 1T en (a) FePt, (b) Co y (c) Ni.
En la Figura 1 se observa que en materiales con ani-sotropías más altas, el efecto de la resonancia empieza a evidenciarse a frecuencias y campos más altos, como son los casos del FePt (Figura 1a) y del Co (Figura 1b), donde las frecuencias que se requieren para que se presente el efecto de la resonancia son del orden de 102 GHz y 10 GHz. El Ni presenta la menor anisotropía, por lo cual la resonancia se presenta a partir de frecuencias mucho más bajas, del orden de los 100 GHz (Figura 1c). El efecto de la temperatura juega un papel importante en la resonancia ferromagnética. Al mantener fija la frecuencia Ω, y al aumentar paulatinamente la temperatura del material, la magnitud del vector de magnetización va disminuyendo, al igual que la anisotropía, por lo que para evidenciar el efecto de la resonancia se requieren valores cada vez más altos del campo Hz. La absorción de energía para los diferentes materiales también se ve afectada por la temperatura.
A medida que la temperatura aumenta, la absorción para cada material disminuye, como se evidencia en la altura de los picos de resonancia. En la Figura 1b, para el Co a bajas temperaturas se observa un comportamiento un poco diferente: la absorción desde T/TC = 0 aumenta hasta una temperatura del orden de 4,5 TC, a partir de la cual empieza a disminuir. Este comportamiento se debe al modelo que se emplea para describir la magnetización de equilibrio, me. Con este modelo, me permanece casi constante hasta una temperatura de 0,4 TC, disminuyendo muy poco hasta una temperatura de 0,5 TC, lo cual hace que el factor Ω0 /m(T) en el denominador del tensor de susceptibilidad se vea fuertemente afectado.
En la Figura 2 se muestra el gráfico de la componente x de la parte imaginaria del tensor de susceptibilidad como función de la frecuencia y para diferentes temperaturas. Se puede evidenciar que la frecuencia de resonancia para los diferentes materiales disminuye a medida que aumenta la temperatura del sistema, pero dicha disminución se presenta de manera más marcada en materiales con mayor anisotropía.
En la Figura 3 se muestran los gráficos de la componente x de la parte imaginaria del tensor de susceptibilidad como función de la amplitud de campo Hz a una frecuencia Ω de 3500GHz para diferentes temperaturas. En este caso de frecuencias altas para los materiales Ni y Co, se presentan campos de resonancia mucho más altos que los que presenta el material FePt, el cual posee mayor campo de anisotropía.
Figura 3 Componente x de la parte imaginaria del tensor de susceptibilidad magnética como función del campo aplicado para los tres materiales. Las figuras se realizaron para: (a) T = 0, (b) T = 0.4Tc y (c) T = 0.7Tc, todos a una frecuencia Ω de 3500GHz.
La absorción de energía en cada material es diferente: en los materiales Ni y Co se observó que la absorción de energía es diferente en los regímenes de bajas y altas frecuencias. Con bajas frecuencias, como en el caso de la Figura 1, estos materiales presentan mucha más absorción que el material FePt, pero en el régimen de altas frecuencias, la absorción de energía disminuye sustancialmente, como se observa en la Figura 3. Además, en el régimen de altas frecuencias (Co, Ni), con el aumento de la temperatura en el material FePt el campo de resonancia cambia apreciablemente hacia valores más altos, lo que no se presenta en los materiales Co y Ni, con los cuales estos campos cambian muy poco.
Conclusiones
Se analizó teóricamente la resonancia ferromagnética de una partícula magnética anisotrópica a temperatura finita, específicamente con los materiales FePt, Co y Ni. El estudio se hizo empleando la ecuación de Landau-Lifshitz-Bloch. Se encontró que la temperatura tiene un efecto importante en los valores de campo y frecuencia de resonancia. En el régimen de baja frecuencia con el aumento de la temperatura en los tres materiales se presentó un corrimiento en el campo de resonancia hacia valores más altos, acompañado con una disminución en la absorción de energía. En el régimen de alta frecuencia para los materiales Co y Ni, el campo de resonancia no cambió mucho con el aumento de la temperatura, en tanto que en el material FePt el campo resonante aumentó sustancialmente.
En materiales con alta anisotropía el efecto de la resonancia se evidencia solo con valores altos de campo y frecuencia, como es el caso del material FePt. En los materiales con anisotropía más baja, Co y Ni, la resonancia empieza a observarse a valores bajos de campo y frecuencia. En el caso de los materiales Co y Ni se observaron dos regímenes de resonancia a bajas y altas frecuencias. A altas frecuencias en estos materiales se requieren campos resonantes muy altos, incluso más altos que el requerido en el caso del material FePt, que posee una alta anisotropía. Una buena comprensión de los efectos de la temperatura y de la anisotropía cristalina en las propiedades resonantes de sistemas magnéticos es crucial para todas las potenciales aplicaciones tecnológicas en que se requiera la inyección y la absorción de energía.
