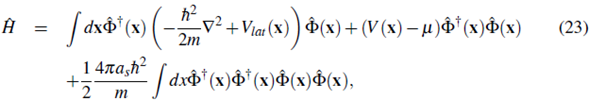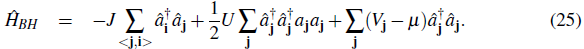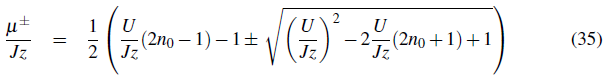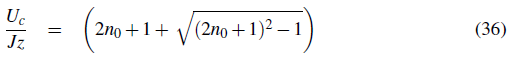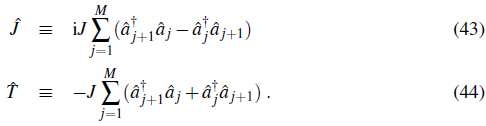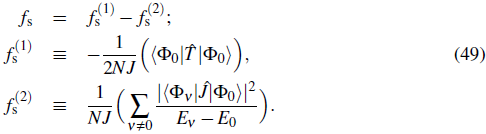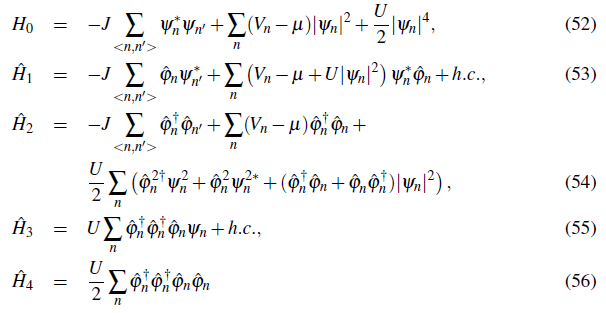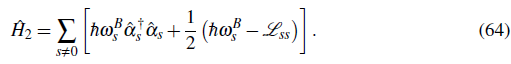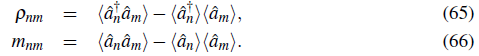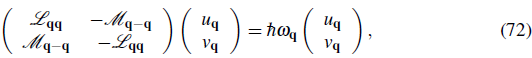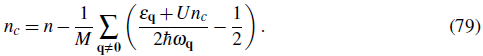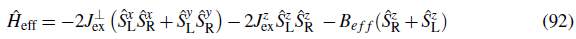Introduction
Ultracold atoms and molecules provide opportunities for studying quantum many-body physics with unprecedented flexibility in the design, control and analysis of experiments. This has been made possible by cooling and trapping techniques that have been developed since the 1980s, by progress in optical control and imaging of atoms and molecules, and by developments in theory and experiment that make possible the independent evaluation of basic atomic and molecular properties.
When atoms are illuminated with laser beams, the oscillating electric field of the lasers induces a dipole moment in the atoms which in turn interacts with the electric field. This interaction modifies the energy of the internal states of the atoms in a way that depends on the light intensity. Therefore, a spatially dependent intensity induces a spatially dependent potential energy which can be used to trap the atoms. This is the basic idea of an optical lattice. Optical lattices have been widely used in atomic physics as a way to trap and cool atoms. In the recent years ultracold atoms in optical lattices have become a unique meeting ground for simulating strongly correlated quantum systems, exploring non-linear phenomena, investigating quantum coherence and generating large-scale entanglement, ultimately leading to quantum information processing in these artificial crystal structures.
This article begins by reviewing the basic physics of atom-light interactions and how they can be used to trap atoms in optical lattices. Then we discuss the behavior of a single atom in a lattice and introduce important concepts such as band structure, Bloch waves and Wannier functions. Finally we discuss theoretical mean field methods commonly used to deal with interacting systems and apply them to calculate the phase diagram of the Bose Hubbard model, an iconic model that describes the behavior of interacting bosons loaded in deep optical lattice potential. After that, we use the introduced techniques to compute quantum correlations and other many body properties of the system. We finalize by discussing the use of ultra-cold atoms in lattice as quantum simulators of quantum magnetism.
1 Materials and Methods
Bose Einstein condensation (BEC) in bosonic gases was predicted by Einstein in 1925 (Einstein, 1925a) based on the quantum statistics ideas developed by Bose for photons (Bose, 1924). The basic idea of BEC is that below a critical temperature a macroscopic number of particles occupy the lowest energy state: as the temperature, T, is decreased the de-Broglie wave length, which scales like T -1/2 , increases and at the critical point it becomes comparable to the inter-particle mean separation. At this point the wave functions of the particles are sufficiently smeared out so that there is always some overlap and a Bose Einstein condensate is formed. Although Einstein's prediction applied for a gas of noninteracting atoms, London suggested that, BEC could be the mechanism underlying the phenomenon of superfluidity in 4He (London, 1938a, 1938b), despite the strong interactions in this system. Further evidence for this point of view came from neutron scattering experiments (Svensson & Sears, 1987).
Experimental efforts to create a BEC in dilute gases date back to the 1980's (Silvera & Walraven, 1980). The first experiments concentrated on using atomic hydrogen but mainly the large rates of inelastic collision prevented these experiments from succeeding. It was not until 1995, using the advances made in laser cooling techniques (Foot, 1991), that BEC in dilute alkali atomic gases was achieved. The first series of experiments were done with rubidium (M. H. Anderson, Ensher, Matthews, Wieman, & Cornell, 1995), sodium (Davis et al., 1995) and lithium (Bradley, Sackett, & Hulet, 1997) vapors. In these experiments atoms are typically collected in a Magneto-Optical Trap (MOT) and compressed and cooled to micro-Kelvin temperatures using laser cooling techniques. They are then subjected to evaporative cooling a process that allows the system to be cooled to nano-Kelvin temperatures. At a critical phase space density BEC takes place. In such a condensate a macroscopic number of atoms, generally up to 106, collectively occupy the lowest energy state.
The experimental realization of BEC in alkali gases opened unique opportunities for exploring quantum phenomena on a macroscopic scale. However, weakly interacting dilute gases described by a mean field picture are the simplest many body systems one can possible find. In order to be in the weakly interacting regime, the ratio between the interaction energy of uncorrelated atoms at a given density, E
int
, and the quantum kinetic energy needed to correlate particles by localizing them within a distance of order of the mean inter-particle distance, E
kin
, must be small. For three dimensional systems E
int
~ n
 (a
s
is the scattering length, which fully characterizes the low energy scattering processes, n is the mean particle density and m is the atomic mass) and E
kin
~
(a
s
is the scattering length, which fully characterizes the low energy scattering processes, n is the mean particle density and m is the atomic mass) and E
kin
~
 n2/3. Thus, the ratio between these two energies is proportional to n
1/3
α
s
. In dilute alkali vapors this ratio is generally of order 0.02. To enter the strongly correlated regime, an obvious way to proceed is either to increase the density or to tune the scattering length. It is indeed possible to tune the scattering length to large values by using a Feshbach resonance. The problem of this approach is, however, that the lifetime of the condensate strongly decreases due to three-body loses. An entirely different way to reach the strongly correlated regime is by using optical lattices (see below). By increasing the depth of the optical lattice the ratio between kinetic energy and potential energy can be changed without changing the scattering length. The idea is that in the presence of an optical lattice the particles can acquire a very large kinetic effective mass,
n2/3. Thus, the ratio between these two energies is proportional to n
1/3
α
s
. In dilute alkali vapors this ratio is generally of order 0.02. To enter the strongly correlated regime, an obvious way to proceed is either to increase the density or to tune the scattering length. It is indeed possible to tune the scattering length to large values by using a Feshbach resonance. The problem of this approach is, however, that the lifetime of the condensate strongly decreases due to three-body loses. An entirely different way to reach the strongly correlated regime is by using optical lattices (see below). By increasing the depth of the optical lattice the ratio between kinetic energy and potential energy can be changed without changing the scattering length. The idea is that in the presence of an optical lattice the particles can acquire a very large kinetic effective mass,
Ekin ~
 n2/3 →Ekin ~
n2/3 →Ekin ~
 n
2/3
with m*~≫m and thus a significantly larger E
int
/E
k¡n
ratio. The beauty of this approach is that the lattice depth can be used as an experimental knob to change the kinetic to interaction energy ratio allowing us to reach different many-body regimes.
n
2/3
with m*~≫m and thus a significantly larger E
int
/E
k¡n
ratio. The beauty of this approach is that the lattice depth can be used as an experimental knob to change the kinetic to interaction energy ratio allowing us to reach different many-body regimes.
1.1 Optical Lattices
Optical lattices are periodic potentials created by light-matter interactions. When an atom interacts with an electromagnetic field, the energy of its internal states depends on the light intensity. Therefore, a spatially dependent intensity induces a spatially dependent potential energy. Optical lattices have been widely used in atomic physics as a way to trap and cool atoms.
Neutral atoms interact with light in both dissipative and conservative way.
The conservative interaction comes from the interaction of the light field with the induced dipole moment of the atom which causes a shift in the potential energy called AC Stark shift.
The dissipative interaction comes due to the absorption of photons followed by spontaneous emission. Laser cooling techniques make use of this dissipative process.
1.1.1 AC Stark Shift
Consider a two level atom, with internal ground state │g〉 and excited state │e〉 separated by an energy ħω
o
. The atom is illuminated with a monocromatic classical electromagnetic field E =
 (x)e
-ivt
+
(x)e
-ivt
+
 *(x)e
m
with amplitude
*(x)e
m
with amplitude
 (x) and angular frequency ω
=
2Πv.
(x) and angular frequency ω
=
2Πv.
The the electromagnetic field interacts with the atomic dipole, given by an operator
 =
μ
eg
│e〉 〈g│
+ μ*
eg
│g〉〈e│, with μ
eg
=
〈e│
=
μ
eg
│e〉 〈g│
+ μ*
eg
│g〉〈e│, with μ
eg
=
〈e│
 │g〉 the dipole matrix elements, and the total Hamiltonian of the system can be written as
│g〉 the dipole matrix elements, and the total Hamiltonian of the system can be written as
Going to the rotating frame, neglecting processes with a rapidly oscillating phase, exp( -i(ω o + ω)), and denoting the laser detuning by ∆ = ω - ω 0 , the total Hamiltonian can be written as
Where Ω.(x) is the Rabi frequency given by ħ Ω (x) = 2
 (x) • μ
ge
.
(x) • μ
ge
.
If the detuning is large compared to the Rabi frequency, │∆│≫ Ω, the effect of the atom-light interactions on the states, │e〉 and │g〉, can be determined with second order perturbation theory. In this case, the energy shift E g,e (2) J is given by
with the plus and minus sign for the │g〉 and │e〉 states respectively. This energy shift is the so called ac-Stark shift. Since the atoms are practically always in the ground state, the energy of the atoms is changed according to the stark shift
 which defines the optical potential.
which defines the optical potential.
Furthermore, if instead of interacting with an monocromatic electromagnetic field, the atoms are illuminated with superimposed counter propagating laser beams, the beams interfere and the interference pattern results in a periodic landscape potential or optical lattice.
1.1.2 Dissipative interaction
In the above discussion we implicitly assumed that the excited state has an infinite life time. However, in reality it will decay by spontaneous emission of photons. This effect can be taken into account phenomenologically by attributing to the excited state an energy with both real an imaginary parts. If the excited state has a life time 1/Γ e , the energy of the perturbed ground state becomes a complex quantity which we can write as
The real part of the energy correspond to the optical potential whereas the imaginary part represents the rate loss rate of atoms from the ground state. The sign of the optical potential seen by the atoms depend on the sign of the detuning. For blue detuning, ∆ > 0, the sign is positive resulting in a repulsive potential, and the potential minima correspond to the points with zero light intensity. On the other hand, in a red detuned light field, ∆ < 0, the potential is attractive and the minima correspond to the places with maximum light intensity.
The optimal detuning for an optical lattice depends on the available laser power I (Ω2 ∝ I) and the maximum dissipative scattering rate that can be tolerated. By using a small detuning it is possible to create larger trap depths for a given laser intensity since the optical potential scales as V ~ I/∆. However, since the inelastic scattering rate scales inversely proportional to the detuning squared as Γe/∆ V, the laser detuning should be chosen as large as possible within the available laser power in order to minimize inelastic scattering processes and create a conservative potential. For large detunings spontaneous emission processes can be neglected and the energy shift can be used to create a conservative trapping potential. This is the physics that describes optical lattices.
1.1.3 Lattice Geometry
The simplest possible lattice is a one dimensional lattice (1D) lattice. It can be created by retro reflecting a laser beam, such that a standing wave interference pattern is created. This results in a Rabi frequency Ω(x) = Ω o sin(kx) which yields a periodic trapping potential given by
where k = 2Π/λ is the the wave vector of the laser light and V 0 is four times times the intensity of a single laser beam without retro-reflection, due to the constructive interference of the lasers.
Periodic potentials in higher dimensions can be created by superimposing more laser beams. To create a two dimensional lattice potential for example, two orthogonal sets of counter propagating laser beams can be used. In this case the lattice potential has the form
Here k is the wave vector of the lattice light, e 1 and e 2 are polarization vectors of the counter propagating set and ¡¡ is the phase between them. If the polarization vectors are not orthogonal and the laser frequencies are the same, they interfere and the potential is changed depending on the time phase. This can be used to tune the geometry of the generated potential. A simple square lattice with one atomic basis can be created by choosing orthogonal polarizations between the standing waves. In this case the interference term vanishes and the resulting potential is just the sum of two superimposed 1D lattice potentials. Even if the polarization of the two pair of beams is the same, they can be made independent by detuning the common frequency of one pair of beams from that the other. Typically a negligible frequency difference compared with the optical frequency is required to achieve independence, thus, even in this case to a good approximation the wave vectors can be considered equal.
A more general class of two 2D lattices can be created from the interference of three laser beams (Blakie & Clark, n.d.; Peil et al., 2003) which in general yield non separable lattices. These kind of lattices can provide tighter on-site confinement, better control over the number of nearest neighbors and significantly reduced tunneling between sites compared with the counter propagating four beam square lattice. In Fig. 1 we show a variety of possible 2D optical lattice geometries that can be made by three and four interfering laser beams. Different type of lattice potentials can be created in 3D by the interference of at least 5 laser beams.
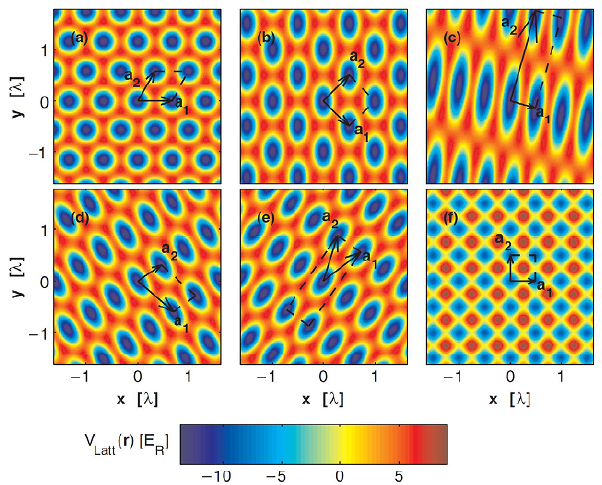
Figura 1 Optical lattices potential. (a) A hexagonal Lattice, (b) A square lattice, (c) A rectangular lattice, (d) An oblique lattice, (e) A centered rectangular lattice, (f) A four beam square lattice. (a)-(e)Lattice potentials are for different configurations of 3 beams, (f) is a potential for the 4 counter-propagating laser beam configuration. This figure is a courtesy of P. Blair Blakie (Blakie & Clark, n.d.)
Results and discussion
Cold atoms interacting with a spatially modulated optical potential resemble in many aspects electrons in the solid crystals ion-lattice potential. However optical lattices have many advantages with respect to solid state systems. Not only they are free from defects but also they can be controlled very easily by changing the laser field properties. Moreover, different from solids where the lattice spacings are generally of order of Amstrongs, lattice constants in optical lattices are typically three order of magnitude larger.
Bloch functions
One of the most important characteristics of a periodic potential is the emergence of a band structure. Consider a one dimensional particle described by the Hamiltonian H =
 + V
lat
(x), where V
lat
(x) = V
lat
(x + a). Bloch's theorem (Ashcroft & Mermin, 1976; Ziman, 1964) states that the eigenstates Φ
q
(n)
(x) can be chosen to have the form of a plane wave times a function with the periodicity of the potential:
+ V
lat
(x), where V
lat
(x) = V
lat
(x + a). Bloch's theorem (Ashcroft & Mermin, 1976; Ziman, 1964) states that the eigenstates Φ
q
(n)
(x) can be chosen to have the form of a plane wave times a function with the periodicity of the potential:
Using this ansatz into the Schrodinger equation, H Φ q (n) (x)= E q (n) (x) Φ q (n) (x), yields an equation for u q (n) (x) given by:
Bloch's theorem introduces a wave vector q. The quantity q should be viewed as a quantum number characteristic of the translational symmetry of the periodic potential, just as the momentum is a quantum number characteristic of the full translational symmetry of the free space. Even though is not the same, it turns out that hq plays the same fundamental role in the dynamics in a periodic potential than the momentum in the absence of the lattice. To emphasize this similarity ħq is called the quasimomentum or crystal momentum . In general the wave vector q is confined to the first Brilloiun zone, i.e. -Π/α < q ≤ Π/α.
The index n appears in Bloch's theorem because for a given q there are many solutions to the Schrodinger equation. Eq. (10) can be seen as a set of eigenvalue problems in a fixed volume, one eigenvalue problem for each q. Therefore, each of them, has an infinite family of solutions with a discretely spaced spectrum with modes labelled by the band index n. On the other hand, because the wave vector q appears only as a parameter in Eq. (10), the energy levels for a fixed n has to vary continuously as q varies. The description of energy levels in a periodic potentials in terms of a family of continuous functions Eq' each with the periodicity of a reciprocal lattice vector, 2Π/α, is referred as the band structure. The lattice potential is generally expressed in units of the atom recoil energy, E R = ħ 2 k 2 /(2m), with k = Π/α.
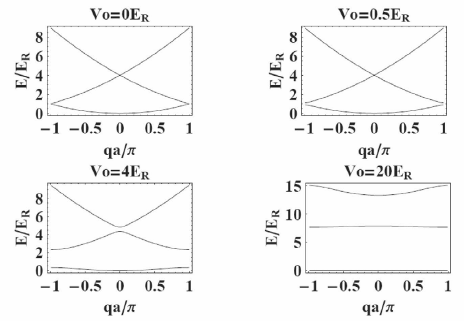
Fig. 2 shows the band structure of a sinusoidal potential. For V0 = 0, the particles are free so the spectrum is quadratic in q. As the potential is increased the band structure appears.The band gap increases and the band width decreases with increasing lattice depth.
In the absence of a lattice the eigenfunctions of the free system are plane waves (see Fig. 3). As the lattice depth is increased the barrier height between adjacent lattices sites increases and the eigenstates of the system tend to get localized at each lattice site (regions around the potential minima).
1.1.4 Wannier orbitais
Wannier orbitals are a set of orthogonal normalized wave functions that fully describe particles in a band and that are localized at the lattice sites. They are defined as:
where the sum is over the first Brillouin zone, M is the total number of lattice sites and x i is the position of the i th lattice site. Wannier orbitals are thus a unitary transformation of the Bloch functions and are formally an equivalent representation to describe the periodic system.
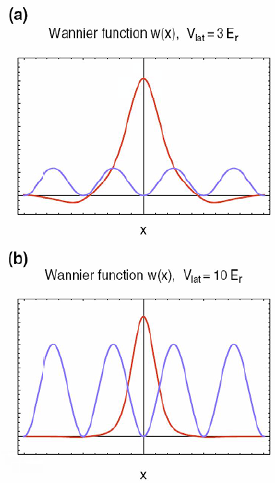
Figura 4 Wannier functions in a periodic potential plotted together with a schematic lattice potential. Wannier functions constitute an orthogonal set of maximally localized wave functions. For the 3E r system shown sidelobes are visible, for 10Er the sidelobes are hardly visible under the scale used in the figure.
The actual form of a Wannier function may be understood if we Eq.(8) to be approximately the same for all Bloch states in a band. Under this approximation the Wannier function at the origin can be shown to be
They look likes u (n) (x) at the site center, but it spreads out with gradually decreasing oscillations with are needed to ensure orhogonality. In Fig. 4 we show a Wannier orbital centered at the origin site.
1.1.5 Tight binding approximation
The tight-binding approximation deals with the case in which the overlap between Wannier orbitals at different sites is enough to require corrections to the picture of isolated particles but not too much as to render the picture of localized wave functions completely irrelevant.
In this regime to a very good approximation one can only take into account overlap between Wannier orbitals in nearest neighbor sites. Furthermore, if initially the atoms are prepared in the lowest band, the dynamics can be represented quite satisfactorily by using Wannier functions of only the lowest band. The tight-binding model is commonly used to solve the problem of a particle in a periodic potential when also an external potential V(x), not strong enough or sharp enough to induce interband transitions, is applied.
By expanding the wave function in lowest band Wannier orbitals,
we get the following equations of motion
with
J is the tunneling matrix element between nearest neighboring lattice sites and ε 0 is the unperturbed on site energy shift. Eq. (14) is known as the discrete Schrodinger equation (DSE) or tight binding Schrodinger equation.
For the special case of a sinusoidal potential V lat (x)= V 0 sin2 (kx) for which Mathieu functions are the exact solutions an analytic expression for J can be obtained:
with α =1.39666, β =1.051 and ү =2.12104 and Ṽ 0 = V 0 /E R . Note that J decreases exponentially with the lattice depth.
1.1.6 Semiclassical dynamics
Solving Eq. (14) is presumably not possible for an arbitrary V(xi). However, we get general insight to the nature of solutions by an application of the correspondence principle. It is well known that wave-packet solutions of the Schrodinger equation behave like classical particles obeying the equations of motion derived from the same classical Hamiltonian. The classical Hamilton equations are
Using the correspondence principle and the resemblance of the crystal momentum or quasi-momentum to real momentum, the semiclassical equations of a wave packet in the first band of a lattice can be written as (Ashcroft & Mermin, 1976; Ziman, 1964)
The semiclassical equations of motion describe how the position and wave vector of a particle evolve in the presence of an external potential entirely in terms of the band structure of the lattice. If we compare the acceleration predicted by the model with the conventional newtonian equation, m
 = -dV(x)/dx, we can associate an effective mass induced by the presence of the lattice, m*. This is given by
= -dV(x)/dx, we can associate an effective mass induced by the presence of the lattice, m*. This is given by
If no external potential is applied, V (x)
=
0, Bloch waves are the solutions of tight binding equation:
 with M is the total number of lattice sites. If also periodic boundary conditions are assumed, the quasimomentum q is restricted to be an integer multiple of
with M is the total number of lattice sites. If also periodic boundary conditions are assumed, the quasimomentum q is restricted to be an integer multiple of
 . The lowest energy band dispersion relation in this case is given by
. The lowest energy band dispersion relation in this case is given by
From the above equation it is possible to see the connection between J and the band width
The effective mass becomes
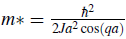 and close to the bottom of the band q → 0, m*→
and close to the bottom of the band q → 0, m*→
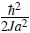 . Since the tunneling decreases exponentially with the lattice depth, the effective mass grows exponentially. In the presence of interactions, the large effective mass manifest itself in a substantial enhancement of the interaction to kinetic energy ratio, in comparison to the free particle case. This is the reason why atoms in optical lattice can reach the strongly interaction regime.
. Since the tunneling decreases exponentially with the lattice depth, the effective mass grows exponentially. In the presence of interactions, the large effective mass manifest itself in a substantial enhancement of the interaction to kinetic energy ratio, in comparison to the free particle case. This is the reason why atoms in optical lattice can reach the strongly interaction regime.
1.2 Bose Hubbard Hamiltonian and the superfluid to Mott insulator transition
The simplest non trivial model that describes interacting bosons in a periodic potential is the Bose Hubbard Hamiltonian. This model has been used to describe many different systems in solid state physics, like short correlation length superconductors, Josephson arrays, critical behavior of 4He and, recently, cold atoms in optical lattices (Jaksch, Brader, Cirac, Gardiner, & Zoller, 1998). It has been studied analytically with many different techniques (Krauth, Caffarel, & Bouchaud, 1992; Sheshadri, Krishnamurthy, Pandit, & Ramakr-ishnan, 1993; van Oosten, van der Straten, & Stoof, 2001; M. P. A. Fisher, Weichman, Grinstein, & Fisher, 1989; Freericks & Monien, 1996) as well as numerically (Batrouni, Scalettar, & Zimanyi, 1990; Scalettar, Batrouni, & Zimanyi, 1991; Niyaz, Scalettar, Fong, & Batrouni, 1991; Batrouni, Scalettar, Zimanyi, & Kampf, 1995; Batrouni et al., 2002). The Bose Hubbard Hamiltonian features a quantum phase transition from a superfluid to a Mott insulator state. This transition has been observed experimentally in ultracold atoms systems in 1D, 2D and 3D lattice geometries(Greiner, Mandel, Esslinger, Hansch, & Bloch, 2002; Paredes et al., 2004; Spielman, Phillips, & Porto, 2007).
We begin the analysis by considering the second quantized Hamiltonian that describes interacting bosonic atoms in an external trapping potential plus lattice. We will assume s-wave interactions which are the relevant interactions in ultra cold gases. In the grand canonical ensemble it is given by:
where
 (x) is the bosonic field operator which creates an atom at the position x, Vi
att
(x) is the periodic lattice potential, V (x) denotes any additional slowly- varying external potential that might be present (such as a harmonic trap), a
s
is the scattering length and m the mass of an atom. μ is the chemical potential which acts as a lagrange multiplier to fix the mean number of atoms in the grand canonical ensemble.
(x) is the bosonic field operator which creates an atom at the position x, Vi
att
(x) is the periodic lattice potential, V (x) denotes any additional slowly- varying external potential that might be present (such as a harmonic trap), a
s
is the scattering length and m the mass of an atom. μ is the chemical potential which acts as a lagrange multiplier to fix the mean number of atoms in the grand canonical ensemble.
Similar to the noninteracting situation where we used Wannier orbitals to span the single particle wave function, it is convenient to span the field operator in terms of Wannier or-bitals. Assuming that the vibrational energy splitting between bands is the largest energy scale of the problem, a conditions which can be fulfilled in most of the experiments, atoms only populate the lowest band and one can restrict the expansion to include only lowest band Wannier orbitals w0(x),
Here âj is the annihilation operator at site j which obeys bosonic canonical commutation relations. The sum is taken over the total number of lattice sites. If Eq. (24) is inserted in Ĥ and only tunneling between nearest neighbors is considered, we obtain the Bose Hubbard Hamiltonian
Here the notation < j, i > restricts the sum to nearest neighbors sites. J given by Eq.(15) and
The first term in the Hamiltonian proportional to J is a measure of the kinetic energy of the system. Next-to-nearest neighbor tunneling amplitudes are typically two orders of magnitude smaller than nearest neighbor ones in the tight-binding limit and to a good approximation they can be neglected.
The second term determines the interaction energy of the system. The parameter U measures the strength of the repulsion of two atoms at lattice site j. The integral (26) is not as sensitive as Eq. (15) to the oscillatory tails characteristic of the Wannier orbitals, and a Gaussian approximation can be used to estimate it (Jaksch et al., 1998). Under the Gaussian approximation, the ground state wave function centered at the origin of a separable sinusoidal lattice, with lattice depth V
α
in the α
=
x, y, z direction, has the form

 with Using this ansatz in the integral (26) yields an onsite interaction given by
with Using this ansatz in the integral (26) yields an onsite interaction given by
with the bar indicating the geometric mean. As the intensity of the lattice is increased the tunneling rate decreases exponentially and the onside interaction increases as a power law, V 0 d/4, (d is the dimensionality of the lattice).
The third term in the Hamiltonian takes into account the energy offset at site j due to a slow varying external potential V (x).
1.2.1 Superfluid Mott insulator transition
At zero temperature the physics described by the Bose Hubbard Hamiltonian can be divided in two different regimes. The interaction dominated regime when J is much smaller than U, and the system is in the Mott insulator phase, and the kinetic energy dominated regime, when tunneling overwhelms the repulsion and the system exhibits superfluid properties. The transition between the two regimes is a consequence of the competition between the kinetic energy which tries to delocalize the particles and the interaction energy which tries to localize them and to make the number fluctuations small.
In the superfluid regime, the kinetic energy term dominates the Hamiltonian and the system behaves as a weakly interacting Bose gas. Quantum fluctuations can be neglected and the system can be described by a macroscopic wave function. For the translationally invariant case the ground state consists of all atoms in the 0-quasimomentum mode
where N is the total number of atoms and
 is the anhihilation operator of an atom with quasimomentum. Remember α is the lattice spacing.
is the anhihilation operator of an atom with quasimomentum. Remember α is the lattice spacing.
Since the many body state is almost a product over identical single particle wave functions the system has a well defined phase and large number fluctuations ~
 . The macroscopic occupation of a single mode implies that the commutator of the annihilation and creation operators that create and destroy a particle in the condensate mode can be neglected with respect to the total number of atoms in the mode. Therefore, to a good approximation the field operator can be replaced by a c-number,
. The macroscopic occupation of a single mode implies that the commutator of the annihilation and creation operators that create and destroy a particle in the condensate mode can be neglected with respect to the total number of atoms in the mode. Therefore, to a good approximation the field operator can be replaced by a c-number,
This procedure can be interpreted as giving to the field operator a non zero average, 〈
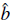 0〉 =
0〉 =
 , and thus a well defined phase to system. Because the original Hamiltonian is invariant under global phase transformation, this definition of BEC corresponds to an spontaneous symmetry breaking (Bogoliubov, 1947; Dalfovo, Giorgini, & Stringari, 1999; P. W. Anderson, 1966; Leggett, 2001; Leggett & Sols, 1991). The wave function associated with the condensate mode, in this case the zero quasi-momentum eigenstate
, and thus a well defined phase to system. Because the original Hamiltonian is invariant under global phase transformation, this definition of BEC corresponds to an spontaneous symmetry breaking (Bogoliubov, 1947; Dalfovo, Giorgini, & Stringari, 1999; P. W. Anderson, 1966; Leggett, 2001; Leggett & Sols, 1991). The wave function associated with the condensate mode, in this case the zero quasi-momentum eigenstate
 is often called "condensate wave function". It characterizes the off-diagonal long range order present in the one particle density matrix (Ginzburg & Landau, 1950; Penrose & On-sager, 1956).
is often called "condensate wave function". It characterizes the off-diagonal long range order present in the one particle density matrix (Ginzburg & Landau, 1950; Penrose & On-sager, 1956).
Strictly speaking, in finite size systems with well defined number of particles neither the concept of broken symmetry, nor the one of off-diagonal long range order can be applied. However the condensate wave function can still be determined by diagonalization of the one particle density matrix. The eigenstate with larger eigenvalue corresponds to the condensate wave function.
As interaction increases the average kinetic energy required for an atom to hop from one site to the next becomes insufficient to overcome the energy cost. Atoms tend to get localize at individual lattice sites and number fluctuations are reduced. Deep in the Mott insulator phase the ground state of the system instead consist of localized atomic wave functions with a fixed number of atoms per site.
where n 0 = N/M is the filling factor or mean number of particles per site. We have assumed that the number of particles is commensurate with lattice sites, i.e. that n 0 is an integer.
The lowest lying excitations that conserve particle number are particle-hole excitations (adding plus removing a particle from the system). The Mott phase is characterized by the existence of an energy gap. The gap is determined by the energy necessary to create one particle-hole pair.
1.2.2 Mean Field Phase diagram
The zero temperature Bose-Hubbard phase diagram (M. P. A. Fisher et al., 1989; Krauth et al., 1992) of a translational invariant system Vj = 0 exhibits lobe-like Mott insulating phases in the J-μ plane, see Fig. 5. Each Mott lobe is characterized by having a fixed integer density. Inside these lobes the compressibility, ∂ρ/∂μ with ρ the average density of the system, vanishes.
The physics behind this diagram can be understood as follows: If we start at some point in the Mott insulating phase and increase μ while keeping J fixed, there is going to be a point at which the kinetic energy of adding an extra particle and letting it hop around will balance the interaction energy cost. With an extra particle free to move around the lattice phase coherence is recovered and the system enters the superfluid regime. Similarly, by decreasing μ from a point in the Mott phase, at some point eventually it will be energetically favorable to remove one particle from the system. The extra mobile hole will induce also phase coherence and the system will condense in a superfluid state. Since the kinetic energy of the system increases with J, the width of the lobes decreases with J. The distance in the μ direction at fixed J between the upper and lower part of the lobe is the energy gap. At J = 0 the gap is just equal to U. Also at J = 0 the intersection points between the lobes with density p = n 0 and the ones with density ρ = n 0 + 1 are degenerated. Because there is not energy barrier to the addition of an extra particle at this generated points the system remain superfluid. Mott insulator phases occur only at integer densities, non-integer densities contours lie entirely in the superfluid phase because there is always an extra particle that can hop without energy cost.
The phase diagram includes two different types of phase transition. One type takes place at any generic point of the phase boundary, and it is driven by the energy cost to add or subtract small numbers of particles to the incompressible Mott state as explained above. On the other hand, the other type only occurs at fixed integer density and takes place at the tip of the lobes. This transition is driven at fixed density by decreasing U/J and enabling the bosons to overcome the on site repulsion. The two kinds of phase transition belong to different universality classes. In the generic one, the parameter equivalent to the reduced temperature δ = T - T c for finite temperature transitions that measures the distance from the transition is δ ~ μ- μ c , with μ c the chemical potential at the phase boundary. For the special fixed density, on the other hand, one must take δ ~ (J/U ) - (J/U)c. As shown in M. P. A. Fisher et al. (1989) provided δ ~ μ - μ c , the compressibility has a singular part scaling near the transition as δ -α , α > 0. This scaling does not apply at the special fixed density Mott-Superfluid transition for which δ ~ (J/U ) - (J/U ) c and differentiation with respect to delta becomes inequivalent to differentiation with respect to the chemical potential.
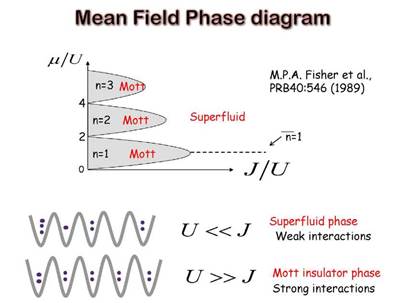
Figura 5 Zero temperature phase diagram of the Superfluid to Mott insulator transition. The dashed lines are contours with fixed integer density.
Most of the features of the phase diagram discussed above can be verified by simple calculations done using a decoupling mean field approximation. Under the decoupling approximation one introduces a real superfluid order parameter ψ =
 =
=
 , and constructs a consistent mean-field theory by substituting the kinetic energy term by
, and constructs a consistent mean-field theory by substituting the kinetic energy term by
into Eq. 25. This yields
where z = 2d is the number of nearest-neighbor sites. This Hamiltonian is diagonal with respect to the site index j, so we can use an effective onsite Hamiltonian. We will therefore drop the subscript j in the following.
By treating ψ as the perturbation parameter one can use perturbation theory to calculate the mean field energy. Assuming commensurate filling N/M = n 0 = 1,2,... , to zero order in ψ the ground state of the system will have energy E (0) no and exactly n 0 particles per site (Eq. 32). In this unperturbed occupation number basis the odd powers of the expansion of the energy in ψ will always be zero. Up to four order the ground state energy becomes
If we now follow the usual Landau procedure for second order phase transitions and minimize Eq. 34 with respect to the superfluid order parameter ψ, we find that ψ ≠ 0 when E (2) < 0 and that ψ = 0 when E (2) < 0. This means that E (2) = 0 signifies the boundary between the superfluid and the insulator phases. The solution E (2) = 0 occurs for
By equating μ + = μ- one finds the point of smallest U for each lobe which corresponds to the critical value at the tip:
1.2.3 The Bose Hubbard model and Superfluidity
The concept of superfluidity is closely related to the existence of a condensate in the interacting many-body system. Formally, the one-body density matrix ρ
(1)
(x, x') has to have exactly one macroscopic eigenvalue whichs defines the number of particles in the condensate; the corresponding eigenvector describes the condensate wave function Φ0 (x) =
 . A spatially varying condensate phase, Θ (x), is associated with a velocity field for the condensate by
. A spatially varying condensate phase, Θ (x), is associated with a velocity field for the condensate by
This irrotational velocity field is identified with the velocity of the superfluid flow, v s (x) = v0 (x) (Leggett, 1999; Lifshitz & Pitaevskii, 1980) and enables us to derive an expression for the superfluid fraction, f s . Consider a system with a finite linear dimension, L along the e1-direction, and a ground-state energy, E0, calculated with periodic boundary conditions. Now we impose a linear phase variation, Θ (x) = θx 1 /L with a total twist angle θ over the length of the system in the e1-direction. The resulting ground-state energy, E θ will depend on the phase twist. For very small twist angles, θ«Π, the energy difference, E 9 - E0, can be attributed to the kinetic energy, T s , of the superflow generated by the phase gradient. Thus,
where m is the mass of a single particle and N is the total number of particles so that mN f s is the total mass of the superfluid component. Replacing the superfluid velocity, vs with the phase gradient according to Eq. (37) leads to a fundamental relation for the superfluid fraction.
where the second equality applies to a one dimensional lattice system on which a linear phase variation has been imposed. Here the distance between sites is α, the phase variation over this distance is ∆θ, and the number of sites is M. In this case, J = ħ 2 /(2ma2).
Technically the phase variation can be imposed through so-called twisted boundary conditions (M. E. Fisher, Barber,& Jasnow, 1973). In the context of the discrete Bose-Hubbard model it is, however, more convenient to map the phase variation by means of a unitary transformation onto the Hamiltonian (Roth & Burnett, 2003; Rey et al., 2003). The resulting "twisted" Hamiltonian in this case
exhibits additional phase factors e±i∆θ - the so-called Peierls phase factors - in the hopping term. We calculate the change in energy E θ - E θ under the assumption that the phase change ∆θ is small so that we can write:
Using this expansion the twisted Hamiltonian (40) takes the following form:
where we retain terms up to second order in ∆θ. The current operator
 (Note that the physical current is given by this expression multiplied by
(Note that the physical current is given by this expression multiplied by
 ) and the hopping operator
) and the hopping operator
 are given by:
are given by:
The change in the energy E θ - E 0 due to the imposed phase twist can now be evaluated in second order perturbation theory
The first order contribution to the energy change is proportional to the expectation value of the hopping operator
Here │ψ0〉 is the ground state of the original Bose-Hubbard Hamiltonian. The second order term is related to the matrix elements of the current operator involving the excited states │Φ0〉 (v = i, 2,...) of the original Hamiltonian
Thus we obtain for the energy change up to second order in ∆θ
The quantity D, defined above, is formally equivalent to the Drude weight used to specify the DC conductivity of charged fermionic systems (Shastry & Sutherland, i990). The superfluid fraction is then given by the contribution of both the first and second order term:
In general both, the first and the second order term contribute. The superfluid fraction is 1 for the noninteracting system and decreases slowly for small U/J. In the region of the Mott transition f s drops rapidly and goes to zero in the Mott-insulator phase. The rapid decrease of the total superfluid fraction is largely due to the second order contribution.
1.2.4 Bogoliuov treatment of the superfluid to Mott transition
As mentioned before the Bose Hubbard Hamiltonian is the simples model that describes interacting bosons in a lattice. Even though the Hamiltonian looks simple in general it is very difficult to deal with exactly and perturbative or approximated treatments are in order. A systematic approach to deal with the weakly interacting regime uses the ideas proposed by Bogoliubov in 1947 (Bogoliubov, 1947). The Bogoliubov approximation starts by treating the field operator as a c-number plus a small fluctuating term. The c-number describes the condensate or the coherent part of the matter field and the fluctuating term accounts for quantum correlations. Since in a weakly interacting gas, quantum fluctuations are small, one can neglect third and higher terms in the fluctuating field and derive an effective quadratic Hamiltonian in the fluctuating field which can be exactly diagonalized.
In the following, we will apply the Bogoliubov approximation to the Bose Hubbard Hamiltonian and derive the correspondent Bogoliubov-de Genes(BdG) equations as developed in Refs. (van Oosten et al., 2001; Roth & Burnett, 2003; Rey et al., 2003). We will restrict our analysis to zero temperature T = 0.
In the very weakly interacting regime, to a good approximation, the field operator can be written in terms of a c-number plus a fluctuation operator:
Replacing this expression for â n in the Bose Hubbard Hamiltonian leads to :
with
Where < n, n > restricts the sum over m to nearest neighbors and h.c. stands for the hermitian adjoint. The terms of the Hamiltonian have been grouped in equations according to the number of non condensate operators which they contain.
The first step is the minimization of the energy functional H 0 . This requires the condensate amplitudes ψ n to be a solution of the following non-linear equation,
This equation is known as the discrete nonlinear Schrödinger equation (DNLSE). It is a discrete version of the so called Gross-Pitaevskii equation (GPE) (E. P. Gross, 1961; Pitaevskii, 2003). It can be also obtained by spanning the GPE equation in a Wannier orbital basis and then using the tight binding approximation (see Eq. 14.) If ψ
n
is a solution of Eq. 57 it means that the linear Hamiltonian
 1 vanishes.
1 vanishes.
The quadratic Hamiltonian
 2 allows the leading order effects of the non-condensate atoms to be taken into account.
2 allows the leading order effects of the non-condensate atoms to be taken into account.
 2 can be diagonalized by finding a basis of so-called quasiparticle states which do not interact which each other. Mathematically this involves a linear canonical transformation of the single-particle creation and annihilation operators
2 can be diagonalized by finding a basis of so-called quasiparticle states which do not interact which each other. Mathematically this involves a linear canonical transformation of the single-particle creation and annihilation operators
 and â
n
into quasiparticle operators
and â
n
into quasiparticle operators
 The transformation is what is known as Bogoliubov transformation and is given by
The transformation is what is known as Bogoliubov transformation and is given by
In general the spectrum of fluctuations includes a zero mode. This mode is the Goldstone boson associated with the breaking of global phase invariance by the condensate. The zero mode is essentially non perturbative and it introduces an artificial infrared divergence in low dimensional models. For this reason quadratic approximations are actually improved if the contribution from this mode is neglected all together (Al Khawaja, Andersen, Proukakis, & Stoof, 2002). A different way to deal with the zero mode has been proposed by Refs. (Castin & Dum, 1998; Gardiner, 1997; Morgan, 2000a, 2000b). For simplicity we are going to ignore zero mode fluctuations and restrict the fluctuation operators to act only on the excited states.
The Bogoliubov transformation Eq. 58 is required to be canonical, which means that it preserves the commutation relations and leads to bosonic quasiparticles. To satisfy this, the amplitudes {u s n , v s n } are constrained by the conditions:
The necessary and sufficient conditions that the quasiparticle amplitudes have to fulfill to diagonalize the Hamiltonian are provided by the so called Bogoliubov-de Gennes (BdG) equations
with u
s
= (u
s
1
, u
s
2
,...)
, v
s
= (v
s
1
, v
s
2
,...) and ψ =(ψ1 ψ2,.-). The matrices
 and
and
 are given by
are given by
with δ n1 the Kronecker delta which is one if n = k and zero otherwise. If the BdG equations are satisfied, the quadratic Hamiltonian takes the form
The quasi-particle energies ħω B s come in pairs: if ħω B s is a solution for the amplitudes (us, v s ) then -hmf is also a solution for the amplitudes (v s *,u s *). The solution with zero energy is always a solution and in this case the amplitudes must be proportional to the condensate (v0,u0) ∝ (ψ, ψ). We explicitly exclude the zero mode solution to guarantee that the excitations are orthogonal to the condensate.
To have a complete description of the quadratic Hamiltonian, we define the one-body density fluctuation matrix , ρ nm, and the anomalous average matrix, m nm , as:
The averages denote an ordinary quantum expectation value. In the zero temperature situation, the average is over the ground quasiparticle state given by â s │0〉 = 0 and the p nm and m nm can be written in terms of quasiparticle amplitudes as:
The quantity ρ nn represents the non-condensate population at position n or depletion at position n. If the average number of atoms is N, the depletion and condensate atoms are related by the equation:
To understand many-body effects included in the quadratic approximations we study the case where no external confinement is present, V n = 0. We assume a d dimensional separable square optical lattice with equal tunneling matrix element J in all directions and periodic boundary conditions. The total number of wells is M.
Due to the translational symmetry of the system the condensate amplitudes are constant over the lattice, ψ
n
=
 . The quasiparticle modes have a plane wave character and therefore can be related to quasimomentum modes:
. The quasiparticle modes have a plane wave character and therefore can be related to quasimomentum modes:
Here the vector q denotes the quasi-momentum whose components assume discrete values which are integer multiples of
 m with a is the lattice spacing. The amplitudes u
q
and v
q
m with a is the lattice spacing. The amplitudes u
q
and v
q
must satisfy the condition │uq│2 -│vq│2 = 1 and can all be chosen to be real and to depend only on the modulus of the wave vector (uq = u-q, vq = v -q ).
In the translationally invariant system the DNLSE reduces to
where z is the number of nearest neighbors z = 2d.
The BdG equations become the following 2 x 2 eigenvalue problem
with
Here we have introduced the definition ε
q
=

The quasiparticle energies ħω q and modes are found by diagonalizing Eq.(73):
And
with n the total density, n = N/M. The constrain that fixes the number of particles can be written as
As opposed to the free particle system where for high momentum always the single particle energy (which grows as q
2
) is dominant, in the presence of the lattice the single particle excitations are always bounded by 4Jd. Therefore, in the regime Un
c
/J > 1 the interaction term dominates for all quasimomentum and so ħω
q
~
 . On the other hand, in the weakly interacting regime, the most important contribution to the sum comes from the low lying modes. For these modes is also true that ħω
q
~
. On the other hand, in the weakly interacting regime, the most important contribution to the sum comes from the low lying modes. For these modes is also true that ħω
q
~
 . Thus, to a good approximation the condensate fraction can be written as:
. Thus, to a good approximation the condensate fraction can be written as:
with
In Eq.(82) the term
 is a finite size effect term which is important to keep for low density systems. α is a dimensionless quantity which depends only on the dimensionality of the system. In the thermodynamics limit, M → ∞ the sum can be replaced by an integral and we find
is a finite size effect term which is important to keep for low density systems. α is a dimensionless quantity which depends only on the dimensionality of the system. In the thermodynamics limit, M → ∞ the sum can be replaced by an integral and we find
The infrared divergency in the one dimensional thermodynamic limit is a consequence of the importance of long wave length correlations in low dimensional systems. For finite one dimensional systems however α (1, M) has a finite value.
Because Eqs. ((74)-(75)) are completely determined if n c is known, by solving Eq. (80) we obtain all necessary information. The solution of the algebraic equation is:
Eq. (86) tells us that for very weak interactions almost all the atoms are in the condensate. As interaction increases the condensate fraction decreases but it only vanishes when U/J → ∞. The BdG equations therefore fail to predict any superfluid to Mott insulator phase transition. Since for non integer fillings the system is never a Mott insulator the BdG equations describe much better incommensurate systems.
1.2.5 External trapping potential
Up to this point we have discussed the basic aspects of the superfluid-Mott insulator transition in a translationally invariant system. The situation is different for a inhomogeneous system with a fixed total number of atoms and external confinement. This is the case realized in experiments, where besides the lattice there is a harmonic trap that collects the atoms at the center. In this case the density of atoms is not fixed since the atoms can redistribute over the lattice and change the local filling factor.
To deal with the inhomogeneous case, it is possible to define an effective local chemical potential, μj = μ , - Vj, at each lattice site j. If the change in the mean number of atoms between neighboring sites is small, the system can be treated locally as an homogeneous system. Because in the inhomogeneous case, the local chemical potential is fixed by the density, as the ratio U/J is changed the system can cross locally the boundary between the superfluid and Mott insulator phases. For example if the chemical potential at the trap center falls into the n 0 = 2 Mott lobe, one obtains a series of Mott domains separated by a superfluid by moving to the boundary of the trap mimicking a wedding cake. In this manner, all different phases that exist for given J/U are present simultaneously.
The existence of such wedding-cake-like density profiles of a Mott insulator is supported by Monte Carlo calculations in one, two, and three dimensions. It has been pointed out recently nevertheless that at the quantitative level the local density approximation is not fully correct (Rigol, Batrouni, Rousseau, & Scalettar, 2009) and corrections of the local density approximation have been measured in 2D systems (Jimenez-Garcia et al., 2010).
The shell structure has been experimentally measured by using indirect methods such as mean field shifts (G. K. Campbell et al., 2006) and spatially selective microwave transitions together with spin changing collisions (Fölling, Widera, Müller, Gerbier, & Bloch, 2006). Just recently direct insituo imaging methods with single lattice site addressability have successfully resolved the shell structure in 2D systems (Gemelke, Zhang, Hung, & Chin, 2009; Bakr et al., 2010; Sherson, Weitenberg, Endres, Cheneau, & Bloch, 2010)
So far we have restricted our analysis to spinless bosons. In the following we will consider the more general situation in which the bosons carry an additional spin degree of freedom and discuss the application of spinfull bosons towards the investigation of quantum magnetism.
1.3 Quantum magnetism in Cold atom systems
Let me start this section by asking a question. Why are some material ferromagnetic or antiferromagnetic? The origin of magnetic ordering has been a topic of great interest in condensed matter Physics.
Quantum mechanical many-electron systems without interactions universally exhibit para-magnetism (they exhibit magnetic ordering only in the presence of a magnetic field). The origin of quantum magnetism should then be sought in electron-electron interactions. In most solids, however, the dominant part of the interaction between electrons is the Coulomb interaction, which is perfectly spin-independent. We are thus faced with a very interesting and fundamental problem in theoretical physics which is to determine whether spin-independent interactions can be the origin of magnetic ordering.
1.3.1 Exchange interactions
As initially proposed for electrons by Dirac and Fowler (1926, 1929) and Heisenberg (1926, 1928), effective spin-spin interactions can arise due to the interplay between the spin-independent Coulomb repulsion and exchange symmetry and do not require any direct coupling between the spins of the particles. The nature of such spin-exchange interactions is typically short-ranged, since it is governed by the wave function overlap of the underlying electronic orbitals.
The importance of exchange interactions can be already seen in two electron systems such as the excited states of the helium atom with one electron in the hydrogenic ground state Φ
1 and the other in an excited state Φ
0
. Since Coulomb repulsion is spin independent the ground state should be four fold degenerate, i.e. the states │↑, ↑〉, │ ↓, ↓〉, │↑, ↓〉, │ ↓, ↑〉 should have in principle the same energy. However, the Pauli exclusion principle enforces the wave function of fermionic particles to be antisymmetric under exchange and thus only the following configurations are allowed
 = (│Φ
1
Φ
2
〉 - (│Φ
1
Φ
2
〉) x │S
=
1,M
=
±1,0〉 also called orthohelium and
= (│Φ
1
Φ
2
〉 - (│Φ
1
Φ
2
〉) x │S
=
1,M
=
±1,0〉 also called orthohelium and
 (│Φ
1
Φ
2
〉 + (│Φ
1
Φ
2
〉) x │S
=
0,M
=
0〉 the so called parahelium. With │S
=
1,M
=
1〉
=
│ ↑,↑〉, │S
=
1,M
=
-1〉
=
│↓,↓〉 and │S
=
1,M
=
0〉
=
(│Φ
1
Φ
2
〉 + (│Φ
1
Φ
2
〉) x │S
=
0,M
=
0〉 the so called parahelium. With │S
=
1,M
=
1〉
=
│ ↑,↑〉, │S
=
1,M
=
-1〉
=
│↓,↓〉 and │S
=
1,M
=
0〉
=
 (│ ↑,↓〉
+
│ ↓,↑〉), the spin triplet states and │S
=
0,M
=
0〉
=
(│ ↑,↓〉
+
│ ↓,↑〉), the spin triplet states and │S
=
0,M
=
0〉
=
 (│
↑ ↓
〉,- │↓ ,↑ 〉) the singlet state. Since in the singlet spin configuration the electrons tend to be closer due to the spatially symmetric wave functions, the singlet experiences higher interaction energy than the triplets which on the contrast minimize their interaction energy by avoiding each other. Consequently quantum statistics breaks the spin degeneracy and makes the orthohelium (triplets) the lower energy state.
(│
↑ ↓
〉,- │↓ ,↑ 〉) the singlet state. Since in the singlet spin configuration the electrons tend to be closer due to the spatially symmetric wave functions, the singlet experiences higher interaction energy than the triplets which on the contrast minimize their interaction energy by avoiding each other. Consequently quantum statistics breaks the spin degeneracy and makes the orthohelium (triplets) the lower energy state.
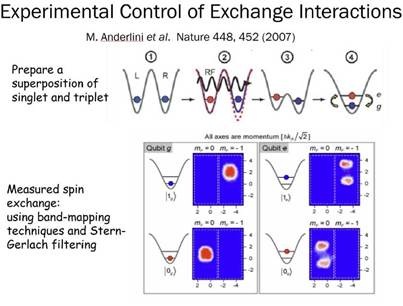
Figura 6 Experimental Control of exchange (Anderlini et al., 2007). Step 1: the system was initialized as qubit state, with one atom in the Right (R) well and one atom in the Left (L) well |1R, 1L). Here 0,1 correspond to two different hyperfine states of the atoms, which were used to encode the spin degree of freedom. Step 2: the two neighboring atoms were transferred to the qubit state |0L, 1R) using site-selective radio-frequency addressing based on the spin-state dependence of the potential (indicated by the differing blue and red potentials). Step 3: the potential barrier between the two sites was then lowered. Step 4: the two sites merged, allowing the atoms to interact. Careful control of the potentials during the merging process pushed the atom in the left site into the first excited state and the atom from the right site into the ground state of the final single-well configuration. Exchange interactions periodically the spin of the ground and excited atoms. The corresponding spin exchange induced oscillations were measured by using band-mapping and a Stern-Gerlach filtering protocol.
The singlet-triplet energy splitting induced by exchange can be modeled by the following spin Hamiltonian
with V ex a coupling constant proportional to the orbital overlap.
While exchange interactions have been extensively discussed in the context of fermions, similar exchange effects also apply to bosons, such as 87Rb with nearly state-independent interactions in the lowest hyperfine manifold F = 1. Except here the particle wavefunctions are symmetrised rather than anti-symmetrised and the singlet state becomes the low energy state. Exchange interactions between pairs of 87Rb atoms were measured and controlled in Anderlini et al. (2007) by initially preparing a Mott insulator state. Actually in the experiment the exchange interactions were used to create entanglement between pair of atoms.
Arrays of paired atoms were isolated and manipulated in the experiment via a double well lattice. This "superlattice" potential can be obtained by superimposing two standing light fields one with twice the periodicity of the other. Within a well the lowest and first vibrational states were used as the Φ 0 and Φ 1 orbitals, and the hyperfine states │F = 1, m F = -1〉, │F = 1, m F = 0〉 as the effective spin states ↑,↓
The steps followed in the experiment are summarized in Fig. 6
In a recent experiment exchange interactions were also probed and utilized for entanglement generation using optical tweezers instead of optical superlattices. See Kaufman et al. (2015) for details.
1.3.2 Superexchange interactions
In several topical insulators, such as ionic solids like e.g. CuO and MnO, however, an-tiferromagnetic order arises even though the wave function overlap between the magnetic ions is practically zero. In this case a "superexchange" interaction can be effective over large distance, as introduced in the seminal works of Kramers and Anderson (Kramers, 1934; P. W. Anderson, 1950). Here, the spin-spin interactions are mediated by higher-order virtual hopping processes, which in the case of bosons (fermions) leads to an (anti)-ferromagnetic coupling between particles on neighboring lattice sites (Auerbach, 1994). Such superexchange interactions are believed to play an important role in the context of high-T c superconductivity (Lee, Nagaosa, & Wen, 2006).
The first time-resolved experimental observation of superexchange interactions in double-well superlattices was reported in Ref. (Trotzky et al., 2008), which we proceed to describe. It used isolated system of two coupled potential wells, which constitutes the simplest concept for the investigation of superexchange-mediated spin dynamics between neighboring atoms. The experiment used a single double well potential occupied by a pair of bosonic atoms with two different spin-states denoted by t and 4-. If the vibrational level splitting in each well is much larger than all other relevant energy scales and intersite interactions are neglected, the system can be described in a two-mode approximation by the Bose-Hubbard-type Hamiltonian which can be written as:
where the operators
 and â
σL
,R create and annihilate an atom with spin σ in the left and right well respectively,
and â
σL
,R create and annihilate an atom with spin σ in the left and right well respectively,
 count the number of atoms per spin-state and well. J
σ
are the tunnel matrix elements (the subscript σ accounts for the fact that in principle the two spin states can see different lattice potentials) and
count the number of atoms per spin-state and well. J
σ
are the tunnel matrix elements (the subscript σ accounts for the fact that in principle the two spin states can see different lattice potentials) and
 are the onsite interaction energies between an atom in spin σ and other in σ'. The state of the system can be described as σ superposition of Fock states {│σ, σ'〉, │σσ', 0〉│0, σσ'〉}, where the left and right side in the notation represent the occupation of the left and right well, respectively, and the states │ σσ ',0〉 and │0, σσ '〉 are spin triplet states (the singlet states require the population of the second band to satisfy the symmetrization of the bosonic wave function and are consequently energetically forbidden).
are the onsite interaction energies between an atom in spin σ and other in σ'. The state of the system can be described as σ superposition of Fock states {│σ, σ'〉, │σσ', 0〉│0, σσ'〉}, where the left and right side in the notation represent the occupation of the left and right well, respectively, and the states │ σσ ',0〉 and │0, σσ '〉 are spin triplet states (the singlet states require the population of the second band to satisfy the symmetrization of the bosonic wave function and are consequently energetically forbidden).
In the limit of dominating interactions (Uσ , σ ' » J), when starting in the subspace of singly occupied wells, the energetically high lying doubly occupied states can only be reached as "virtual" intermediate states in second order tunneling processes. Such processes lead to a nearest neighbor spin-exchange interaction, which couples the states │σ, σ'〉:
These type of processes can be recast in an effective spin Hamiltonian valid for an arbitrary spin configuration (Auerbach, 1994; Duan, Demler, & Lukin, 2003; Kuklov & Svis-tunov, 2003):
where the effective coupling constants are given by
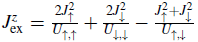
and

 acts as an effective magnetic field. Here constant terms have been dropped. Note that for fermionic particles the same Hamiltonian can be derived but one needs to replace
acts as an effective magnetic field. Here constant terms have been dropped. Note that for fermionic particles the same Hamiltonian can be derived but one needs to replace
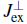 → -
→ -
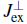 and set the U
σ,σ
terms to infinity, to account for the fermionic statistics.
and set the U
σ,σ
terms to infinity, to account for the fermionic statistics.
For the generic case of spin independent interactions U σ,σ = U (with a very good approximation the case for 87Rb atoms in the hyperfine level F = 1, which was the system used in Trotzky et al. (2008)), and spin independent tunnelings J σ,σ ' = J, one recovers the Heisen-berg Hamiltonian
with Jex =
 . The negative sign is for bosons and favors ferromagnetic correlations. The positive sign is for fermions and favors antiferromagnetism.
. The negative sign is for bosons and favors ferromagnetic correlations. The positive sign is for fermions and favors antiferromagnetism.
Let's now allow for the presence of a bias or a tilt along the double well axis. This is capture by adding to the Hamiltonian a term
When a potential bias ∆ > 0 is applied, the degeneracy of the two intermediate states in the superexchange process is lifted. For J, ∆ «.U this leads to a modification of the effective superexchange coupling with now Jex = J2 / ( U + ∆ )+J 2 /(U - ∆ ) = 2J2 U /(U 2 - ∆2 ). By tuning the bias to A > U, it is possible to change the sign of Jex and therefore to switch between ferromagnetic and antiferromagnetic superexchange interactions. For J << │U - ∆│ the picture of an effective coupling via two virtual intermediate states is again valid.
The measured dynamical observable was time-dependent Neel order parameter or spin imbalance N
z
- (
n↑
L
+
n↓R
-
n↑
R
-
n↓
R
)/2 starting with double wells initially prepared in │↑,↓). Here n↑,↓
;L
,R -〈
 t,;;í,R〉 denote the corresponding quantum mechanical expectation values.
t,;;í,R〉 denote the corresponding quantum mechanical expectation values.
Since the total magnetization operator, Ŝz
L + Ŝz
R, commutes with the Hamiltonian, for the initial conditions in consideration we can restrict the Hilbert space to those states with zero net total magnetization i.e. │↑,↓〉, │↑, ↓〉,│0, ↑↓〉 and │ ↑↓,0〉 . In this case for symmetric double wells (∆ = 0), the Hamiltonian Eq. 90 can be diagonalized analytically to give a valid picture for all values of J and U within the single band Bose-Hubbard model (BHM). A convenient basis is given by the spin triplet and singlet state │t/s〉
=
(│↑,↓〉 ± │↑,↓〉)
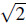 and the states │±〉 ≡ (│↑↓,0〉 ±|0, ↑↓〉)/
and the states │±〉 ≡ (│↑↓,0〉 ±|0, ↑↓〉)/
 . Two of the eigenstates are linear combinations of │t〉 and │+〉, where the one having the larger overlap with │t〉 is the ground state. The spin singlet │s〉 and the state │
-
〉 are already eigenstates themselves with energy 0 and U respectively. As a direct consequence, │
-
〉 cannot be reached from the initial state │↑,↓〉
=
(│s〉
+
│s〉)/
. Two of the eigenstates are linear combinations of │t〉 and │+〉, where the one having the larger overlap with │t〉 is the ground state. The spin singlet │s〉 and the state │
-
〉 are already eigenstates themselves with energy 0 and U respectively. As a direct consequence, │
-
〉 cannot be reached from the initial state │↑,↓〉
=
(│s〉
+
│s〉)/
 . Therefore, the dynamical evolution of the spin imbalance contains only two frequencies
. Therefore, the dynamical evolution of the spin imbalance contains only two frequencies
The extraction of these frequencies from time-resolved measurements allows for the determination of 2J = ħ
 and U = ħ(ω
1
- ω
2
) within the BHM.
and U = ħ(ω
1
- ω
2
) within the BHM.
In order to investigate the spin dynamics atoms in Trotzky et al. (2008) atoms were prepared in a 3D array of double wells with a Neel-type antiferromagnetic order, │↑,↓〉, in each double-well. After rapidly ramping down the short lattice and thereby the double well barrier the system was let to evolve for a hold time t, after which the spin-configuration was frozen out by ramping up the barrier and then the ensemble average N z (t) measured.
Two typical time traces characterized the dynamics. For low barrier depths (J/U > 1), there was a pronounced time evolution of the spin imbalance N z (t) consisting of two frequency components with comparable amplitudes and frequencies. With increasing interaction energy U relative to J, the frequency ratio increased, leaving a slow component with almost full amplitude and an additional high-frequency modulation with small amplitude (Fig. 1.3.2). For J/U«1, the fast modulation is completely suppressed and the only process visible was the superexchange oscillation.
1.3.3 Extended Bose-Hubbard Model
The inclusion of next-neighbor interactions to the simple BHM Hamiltonian defined in Eq. 90 leads to the extended Bose-Hubbard-type Hamiltonian. For simplicity let's focus on the experimentally relevant case of two coupled wells occupied by exactly two atoms in the two different spin-states │↑〉 and │↓〉
where ULR corresponds to the inter-well interaction energy ULR = and AJ =
 and ∆J=
and ∆J=
 . It is apparent that those terms in Eq. 96 proportional to AJ act in the same way on an arbitrary Fock state in the system as the tunneling operator does and therefore modify J to
J'
=
J
+
∆J,
while the terms proportional to ULR lead to an energy shift of the states with exactly one atom on each site with respect to the states with double occupancy in a single well. The states │s〉 and
│
-
〉 stay eigenstates of the system and the states │t〉 and │+〉 are now coupled via the matrix
. It is apparent that those terms in Eq. 96 proportional to AJ act in the same way on an arbitrary Fock state in the system as the tunneling operator does and therefore modify J to
J'
=
J
+
∆J,
while the terms proportional to ULR lead to an energy shift of the states with exactly one atom on each site with respect to the states with double occupancy in a single well. The states │s〉 and
│
-
〉 stay eigenstates of the system and the states │t〉 and │+〉 are now coupled via the matrix
with the eigenvalues
In the regime of strong interactions, the frequency ω 2 is assigned to the superexchange process and by means of perturbation theory up to second order, one finds the effective coupling parameter to be J'ex = 2J' /U - ULR. The direct spin-exchange term ULR favors an antiferromagnetic ground state for repulsively interacting bosons. However the case ULR > 2J' 2 /U is never reached and the ground state remains always ferromagnetic for bosons (anti-ferromagnetic for fermions). This is in agreement with the Lieb-Mattis theorem, which states that the ground state of two bosons in a spin independent potential is a spin triplet state. Experimentally deviations from the simple BHM were observed in Trotzky et al. (2008). In fact, the EBHM description yields ħ(ω 1 -ω 2 ) = U + 3ULR which better described the experimentally measured frequency difference for small short-lattice depths.
2 Conclusions
We discussed the basic physics that rules the quantum behavior of ultra-cold bosonic gases loaded in optical lattice, starting from their single particle behavior and going into the main properties that characterize the strongly interacting regime. Here we focused on describing the basic tools developed by the atomic physics community in the last few decades, with the mere purpose of introducing the basic concepts and to motive the interested reader to delve and follow up onto more recent developments accomplished on these systems. In fact, quantum simulation with ultracold atoms in optical lattices is now starting to reach the level of maturity necessary for the use of these systems for the investigation of complex quantum behavior in regimes not accessible to classical computers. In particular, the improved control of interactions and confinement (C. Gross & Bloch, 2017; Schafer, Fukuhara, Sugawa, Takasu, & Takahashi, 2020), and the development of improved site-resolved techniques such as quantum gas microscopes (C. Gross & Bloch, 2017; Schafer et al., 2020) and exquisite energy resolution allowed by state-of-the-art optical lattice clocks (S. L. Campbell et al., 2017), are opening untapped opportunities towards the design and engineering of synthetic quantum materials with capabilities beyond the ones offered by real materials. It is clear that there is a great vista ahead and new exciting developments to come in next generation experiments.