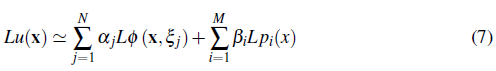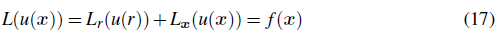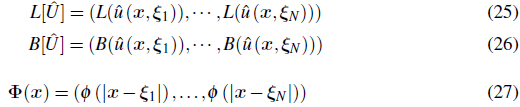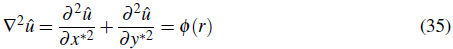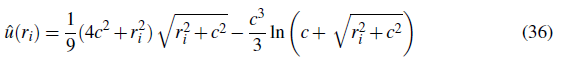Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introducción
El modelado y simulation numérica en la dinámica de fluidos y en los fenómenos de transporte, ha sido un tema relevante de investigation debido a su ocurrencia en diferentes aplicaciones de ingeniería. Una comprensión detallada de los fenómenos de transporte es un aspecto fundamental a la hora de diseñar, optimizar o mejorar los sistemas, y requiere la solution de modelos matemáticos basados en ecuaciones diferenciales ordinarias (EDO) o parciales (EDP) (Chejne J, 2016). Los métodos numéricos para resolver estos modelos se han convertido en una herramienta eficaz porque permiten obtener una description de las variables como la temperatura, presión y velocidad resolviendo las ecuaciones de conservación en su forma diferencial.
Los métodos numéricos tradicionales y más usuales para la solution de las ecuaciones diferenciales parciales en la dinámica de fluidos y fenómenos de transporte, son el método de diferencias finitas (Finite difference method FDM), elementos finitos (Finite element method FEM) y el método de elementos de frontera (Boundary element method BEM). Todos ellos poseen ventajas y desventajas, así como diferencias en la complejidad de su programación y su adaptabilidad a ciertos tipos de problemas. Sin embargo, el FDM requiere mallas rectangulares o estructuradas y por lo tanto es difícil de aplicar en dominios irregulares. FEM por su parte es más flexible geométricamente pero el mallado y la formulación pueden ser complejos. BEM es un método poderoso y semianalítico basado en funciones de Green y formulaciones integrales, pero está limitado por la disponibilidad o existencia de la solución fundamental de las ecuaciones gobernantes del problema y requiere aproximaciones especiales para los términos no lineales o las integrales de dominio.
En contraste con los métodos anteriores, los métodos sin malla (meshless) son esquemas de aproximación numérica que utilizan colocación de los operadores diferenciales en un conjunto de puntos o nodos, para aproximar la solution de ecuaciones diferenciales parciales u ordinarias usando posiblemente funciones de base radial (Zerroukat, Power, y Chen, 1998a). Estos esquemas actúan de manera similar a diferencias finitas pero con puntos distribuidos de maneras flexible, inclusive aleatorios o agrupados en subconjuntos mas pequenos (esténciles), en lugar de un sistema de cuadrícula regular. Esto permite por una parte, la solución numérica de problemas con geometrías complejas en cualquier número de dimensiones sin dificultad adicional, y de problemas descritos con modelos complejos que requieren una solución e implementación más directa.
Una función de base radial (Radial basis función RBF), es una función real cuyo valor depende de la distancia entre dos puntos o nodos, un nodo fuente que actúa como centro y un nodo de campo o punto donde se evalúa la función. La norma usada para la distancia es frecuentemente la norma euclidiana aunque otras pueden ser admisibles en aplicaciones especificas (Aftab, Moinuddin, y Shaikh, 2014) o en problemas sobre manifolds (Hubbert, L.Gia, y Morton, 2015; Levesley y Ragozin, 2007).
El método de interpolación RBF se considera una técnica numérica optima para interpolar datos dispersos multidimensionales (Powell, 1994; W.Madych y Nelson, 1990). Sin embargo, su aplicación trasciende la interpolación porque tambien se utilizan ampliamente para resolver ecuaciones diferenciales parciales, ya sea por sí mismas como un método sin malla puntual (Jumarhon, Amini, y Chen, 2000; Kansa, 1990) o combinadas con otros métodos tradicionales para mejorar su precisión (Orsini, Power, Morvan, y Lees, 2010).
Existen varias formulaciones (Stevens y Power, 2015) o técnicas de aplicación de los métodos de colocación con RBF, que se diferencian entre sí en la precisión numérica de la solución, la eficiencia computacional, la forma de aproximación discreta de los operadores diferenciales y el número de condición de las matrices. Entre estos, destacan los métodos globales, locales, métodos herméticos, métodos de soluciones particulares aproximadas, cuadraturas diferenciales y formulaciones directas e indirectas entre otros.
El método de colocación directa con RBF, sugerido originalmente por Edward Kansa (Kansa, 1990), se ha utilizado con éxito para la solution de varios problemas de valores de frontera gobernados por diferentes ecuaciones diferenciales parciales. Como ejemplos básicos de implementaciones del método de Kansa, se pueden mencionar la solución de la ecuación de Laplace (Kansa, 1990), problemas de Poisson y Helmholtz (Chantasiriwan, 2004; Mai-Duy y Tran-Cong, 2002), difusion y conveccion (Boztosun y Charafi, 2002), y las ecuaciones de Navier-Stokes (Chinchapatnam, Djidjeli, y Nair, 2007) entre otros. Las principales ventajas de las estrategias de colocación RBF son el carácter sin malla de la aproximación, la independencia dimensional de la formulación y la convergencia espectral de algunos de los interpolantes RBF como la función multicuadrica (MQ) (W. R.Madych y Nelson, 1990). Sin embargo, los métodos de colocación global con RBF adolecen de un problema fundamental denominado por Robert Schaback (Schaback, 1995) como la relation de incertidumbre: un mejor condicionamiento de las matrices del problema, se asocia con una menor precisión, y un mal condicionamiento se asocia con una mayor precisión. A medida que aumenta el tamaño del sistema, este problema se vuelve más pronunciado.
A pesar del desarrollo en la implementación de enfoques globales, la precisión de los meto-dos directos de colocación global de RBF todavía está limitada por el tamaño de la matriz (completamente poblada o densa) y los problemas de condicionamiento. Para disminuir estas dificultades, se han propuesto diferentes alternativas de interpolation. Entre estos nuevos enfoques, los esquemas basados en interpolaciones con soporte local parecen estar entre los más eficientes, tienen menos sensibilidad a los parámetros de algunas funciones radiales y evitan el problema del mal condicionamiento a nivel local. Adicionalmente puede demostrarse que estos métodos locales constituyen una generalización del método de diferencias finitas superando las limitaciones de mallas estructuradas e introduciendo un orden superior (Kamyabi, Kermani, y Kamyabi, 2019). Sin embargo, en la implementación de las formulaciones locales, se pierde parte del caráter sin malla del esquema numérico, debido a la necesidad de definir la conectividad local parcial de los nodos de interpolación como se propone en los trabajos de Stevens y Power (Stevens, Power, Meng, Howard, y Cliffe, 2013). Las formulaciones locales han resultado ser mas eficientes en muchos problemas, por ejemplo en la prediction de campos de flujo viscoso a un número de Reynolds moderado y alto (Zhang, Chen, Chen, y Li, 2016), y otros casos no lineales como flujo a traves de medios porosos en suelos (Jackson, Power, Giddings, y Stevens, 2017). La solución numérica por RBF de ecuaciones diferenciales parciales también puede mejorarse mediante métodos simétricos hermíticos, que interpolan las variables en los nodos y además aplica y cumple exactamente el operador diferencial en un conjunto de puntos. Esta clase de esquemas, denominados conservativos, se ha aplicado para la interpolation de velocidades garantizando el principio de conservation de masa. Por ejemplo, las derivadas de la velocidad pueden aproximarse en términos de los componentes del campo de velocidad, de tal manera que el balance de masa se satisfaga en el dominio de interpolación como se demuestra en (Wu y Zhang, 2013; Florez, Bustamante, Giraldo, y Hill, 2012).
Uno de los avances más recientes de los métodos mencionados, fue propuesto por Chen (Zhang y cols., 2016; Chen, Fan, y Wen, 2012) y denominado como método de soluciones particulares aproximadas (Aproxímate particular soluciones MAPS), con el objetivo de mejorar las aproximaciones espaciales del método Kansa mediante el uso de soluciones particulares de la ecuación diferencial como funciones de colocación. Basicamente, se construye una EDP auxiliar no homogénea en la que se utilizan funciones de base radial como termino fuente (termino no homogéneo). Las soluciones analíticas particulares obtenidas al resolver el problema auxiliar no homogéneo se utilizan como funciones de colocación. La aplicación de MAPS a las ecuaciones de Stokes y Navier Stokes se expande de manera constante, por ejemplo, en los trabajos de Power y Granados (Granados, Power, y Bustamante, 2018) se aplica para resolver el flujo bajo la influencia de campos magnéticos. Un recuento detallado de la evolucion histórica de MAPS es presentado por Cheng (A. H. D. Cheng y Hong, 2020) junto con un resumen de temas matemáticos formales de unicidad e invertibilidad.
El objetivo de este trabajo es mostrar una revisión general de las principales formulaciones RBF para la solución de modelos matemáticos basados en ecuaciones diferenciales parciales, su evolución, sus diferencias y la forma en que pueden superarse algunas de sus limitaciones. También se presentaran algunos ejemplos de aplicación originales de los métodos descritos en la solución de problemas acoplados de fluidos, para ilustrar de esta manera la potencia, generalidad y simplicidad de los métodos propuestos. Se introducen dos problemas no resueltos previamente mediante métodos locales RBF, por lo cual se extiende el campo de aplicación de estas técnicas: el problema de flujo electro-osmótico bidimensional, resuelto mediante soluciones particulares radiales locales, y el problema de electrohilado, descrito como un sistema algebraico diferencial, ambos temas de importancia actual en ingeniería.
2. Colocación directa con funciones de base radial
La aproximación de la solución u(x) de una ecuación diferencial, en un dominio Ω con frontera Г discretizado en un conjunto de N puntos o nodos S = [x1, x 2 ,...,xN ] C Ω U Г puede ser expresada mediante una expansion de la forma,
donde p¡(x) es un polinomio de grado i y Φ (x) es una función RBF. Toda función continua en un dominio que incluya un conjunto de puntos discretos, puede ser interpolada en el punto x, a partir de sus valores en los puntos vecinos usando la ecuación 1, en términos del radio o distancia r = ║x - ξ i ║ desde un punto fuente o centro ξ i = ξ i1 , ξ i2 ,---, ξ id ) ∈ ℝ d hasta cualquier otro punto x = (x 1 , x 2 ,...,x d ) G R d . siendo d el número de dimensiones del problema, α i y β i los coeficientes que deben ser determinados y Φ i (r) son las funciones de base radial.
Es importante mencionar que debe tenerse especial cuidado en la elección de las funciones radiales Φ(r), ya que esta determina que la ecuación 1 sea una interpolation en el sentido estricto (Schaback, 2007).
La ecuación 1 podría escribirse sin el polinomio de aumentación p(x), pero en ese caso la función Φ debe ser una función incondicionalmente definida positiva (e.g. Gaussiana, multicuadrica, splines de Sobolev o funciones de soporte compacto) para garantizar la existencia de la solución del sistema resultante. Si es así, el sistema lineal de ecuaciones produce un vector de coeficiente único (Buhmann, 2000).
Sin embargo, por lo general se requiere el polinomio adicional cuando las RBF son condicionalmente definidas positivas como en el caso de los splines de placa plana (Zerroukat, Power, y Chen, 1998b).
En el caso de las funciones radiales multicuádricas, estas son, sujetas a un cambio de signo, condicionalmente definidas positivas de orden 1, pero el problema de interpolación radial original sin polinomios de aumentación resulta ser no-singular debido a las propiedades especiales de la función multicuádrica (ver teoremas de Micchelli (Micchelli, 1986)).
Todos estos comentarios son útiles para diversas formas de interpolación y todos pueden aplicarse en varias dimensiones y diversos conjuntos de puntos distintos. Para una discusión más profunda y formal de las implicaciones y significado de la las funciones radiales positivas definidas se remite al lector al teorema de Bochner (Bochner, 1941) y a los trabajos en dimensiones superiores de Wedland (Wendland, 1995; Buhmann, 2000).
Algunas de las funciones radiales más comúnmente usadas se muestran en la tabla 1, donde c es un parámetro de forma ajustable (Wertz, Kansa, y Ling, 2006; Dehghan, Abbas-zadeh, y Mohebbi, 2014). Para determinar los coeficientes α i y βi se aplica el método de colocación, es decir se aplica la ecuación 1 a cada uno de los nodos de dominio para obtener un sistema de ecuaciones de la forma:
o simplemente en forma matricial,
Las últimas filas de la matriz de colocación en la ecuación 2 corresponden a las condiciones de ortogonalidad
necesarias cuando se usan polinomios para garantizar optimalidad del interpolante y que el problema sea bien puesto (Oruç, 2021).
Puede demostrarse (Micchelli (Micchelli, 1986)) que con una elección adecuada de los nodos, la matriz de interpolation no es singular, de hecho el teorema (para demostración ver (Fasshauer, 2007)) establece lo siguiente:
Teorema 2.1. Si la función real Φ (r) es condicionalmente Positiva definida de orden m en ℝ s y los puntos x 1 , x 2 ,..., x N forman un conjunto (m - 1)-unisolvente, el sistema 2 tiene solución única
Es decir, si las columnas correspondientes a los polinomios son linealmente independientes en la matriz de la ecuación 2, se garantiza la existencia de la solución. Sin embargo, Aunque la matriz F sea invertible, su número de condition puede ser extremadamente alto en algunos casos (Orsini, Power, y Lees, 2011; Schaback, 1995).
Los resultados teóricos sobre la existencia de un interpolante en la forma de la ecuación 1 omitiendo los polinomios de aumentación, para el caso de algunas funciones radiales, se basan en el concepto de funciones condicionalmente definidas positivas. Una función Φ (r) es condicionalmente definida positiva de orden m en ℝ d para d ≥ 1 si y solo si,
Si adicionalmente,
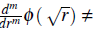constante, la función radial Φ (r) es estrictamente positiva definida y el sistema de ecuaciones de colocación 2 sin incluir los polinomios, tiene solución única. Este resultado para el caso m = 0 fue demostrado por Schoenberg (Schoenberg, 1938; Sarra, 2006) para el caso de las RBF Gaussianas. El gran aporte de Charles Micchelli (Micchelli, 1986) fue extender este resultado para demostrar la invertibilidad de la matriz de colocación sin incluir polinomios para las RBF condicionalmente positiva definidas de orden 1 como las multicuadricas
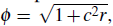dado que (Sarra, 2006),
Otro ejemplo bien conocido surge cuando se toma c = 0 en la función multicuádrica, se tiene entonces la llamada función de base radial lineal 0 (r) = r que también genera un problema de interpolación no-singular sin necesidad de polinomios de aumentación. Micchelli posteriormente extendió esta teoría para incluir funciones radiales condicionalmente definida positivas de orden m ≥ 2, añadiendo los polinomios de aumentación.
En una representación similar cualquier operador diferencial lineal L podra aproximarse al aplicarlo directamente a la ecuación 1:
Por ejemplo, para problemas convección-difusión descritos por la ecuación,
el operador L es,
donde se ha utilizado notación tensorial o convenio de suma de Einstein para los subíndices, V i representa una velocidad de convección, u representa la variable dependiente del problema, por ejemplo temperatura, concentración o velocidad de un fluido y el termino no homogéneo f es el termino fuente del problema físico. El operador diferencial en forma discreta podrá ser obtenido mediante la ecuación 7 así,
3. Diferentes formulaciones del método de colocación
Las principales variaciones del método de colocación para aproximar la solución de una ecuación diferencial, presentado en la ecuación 10, se diferencian basicamente en la forma de la expansión utilizada, las funciones base, las matrices que se generan y el soporte discreto o conjunto de nodos donde se aplica la aproximación. El método más simple de todos, bosquejado en la ecuación 10 es el método de Kansa (Kansa, 1990). En este método, la aproximación se aplica a cada uno de los nodos del dominio y de la frontera, obteniéndose una matriz de coeficientes asimétrica, por eso se le conoce como método global de colocación asimétrico. También se trata de un método que no proporciona directamente los valores de la solución en los nodos, sino que permite obtener los coeficientes α y β a partir de los cuales es necesario reconstruir la solución de la EDP en cualquier punto x usando la ecuación 1. A pesar de varios esfuerzos, la solubilidad del método Kansa carece de una prueba matemática rigurosa (Hon y Schaback, 2001). Una de las maneras de superar las limitaciones del método de Kansa, es el método hermítico. Considere un problema de valores de frontera definido por:
Los operadores L y B son operadores diferenciales parciales lineales en el dominio Ω y en el contorno ∂Ω respectivamente. Fasshauer y Schaback (Fasshauer, 1997; Franke y Schaback, 1998) sugirieron un método de colocación basado en la propiedad de interpolation de Hermite de las funciones de base radial, que establece que las RBF no solo pueden interpolar una función dada sino también sus derivadas. La prueba de convergencia para una interpolación RBF Hermite-Birkhoff fue dada por Wu (Wu, 1998; Franke y Schaback, 1998), quien posteriormente también demostró la convergencia de este enfoque al resolver PDE. En esta formulation, la solución del problema se aproxima por:
donde N es el número total de nodos para la aproximación, nc representa el número de nodos donde se aproxima el valor de la variables u, nb el número de nodos donde se aplican las condiciones de frontera , N - nb - nc el número de nodos internos donde se aplica el operador diferencial y np el número de polinomios de aumentación en caso de usarse. LξyBξ son los operadores diferenciales que actúan sobre Φ vistos como una función del segundo argumento ξ, es decir, son operadores adjuntos. Substituyendo la aproximación de la ecuación 12 en la ecuación diferencial y en las condiciones de frontera 11, y aplicándola tanto en cada uno de los nodos internos como en los de frontera, conduce a un sistema de ecuaciones lineales simétrico del cual se resuelven los coeficientes de la aproximación 12. Dado que la alternativa hermítica con RBF aproxima tanto el valor de la solución como del operador diferencial y los operadores de frontera en diferentes nodos, esta se constituye como una formulation advectiva conservativa implícita (i.e. upwind analítico)(Stevens, Power, y Cliffe, 2013). Como ventaja adicional, se observa que la inclusion de los operadores de frontera en las ec.12, garantiza que las condiciones de frontera se cumplen en forma exacta en aquellos nodos donde sean aplicadas.
Uno de los métodos más recientes es el de soluciones particulares aproximadas (MAPS, method of approximate particular solutions), y su gran ventaja es usar funciones radiales que son soluciones particulares de la ecuación diferencial. En este método se aproxima directamente la EDP, es decir, el operador L(u),enterminos de RBF (Chen y cols., 2012), es decir,
Al integrar esta ecuación diferencial no homogénea, es posible obtener una representación de la variable mediante una superposición de las soluciones particulares correspondientes. De esta forma se define la siguiente aproximación:
donde la solución particular u viene dada por la solución de la ecuación 15, en términos de Φ(r k ). Cuando se aplican las ecuaciones 13 y 14 a cada uno de los nodos internos y de frontera, se obtiene un sistema de ecuaciones escrito en forma matricial,
donde Nb y N representan el número de nodos de frontera y el número total de nodos respectivamente. Como se mencionó anteriormente, una vez se solucióna el sistema de ecuaciones 16 el valor de la solución u(x) en cualquier nodo puede obtenerse directamente a partir de la ecuación 14. El método MAPS puede presentar la dificultad para hallar la solución particular û(r) analíticamente cuando el operador L(u) no posea simetría radial. En estos casos simplemente puede usarse una descomposición de este operador en una componente con simetría radial L r y una componente adicional Lx,
La solución particular û(r) puede encontrarse analíticamente con las técnicas matemáticas usuales de transformadas integrales, variation de los parámetros, entre otros. Un compendio de estas soluciones particulares para varias ecuaciones diferenciales es presentado en (A.-D.Cheng, 2000).
La matriz de colocación en la ecuación, 16 es densa o totalmente poblada y posee problemas de mal condicionamiento a medida que aumenta el número de nodos (Orsini y cols., 2011). Estas características de las matrices de los métodos globales de colocación con RBF, da origen a una relation de incertidumbre donde a medida que se aumenta el número de nodos la precisión mejora, pero el mal condicionamiento también aumenta produciendo sistemas cuasi-singulares y haciendo difícil obtener una solución. Además de los problemas mencionados, las matrices densamente pobladas requieren considerables recursos computacionales de almacenamiento, procesamiento y tiempo de cómputo para la solución. Por lo tanto, las formulaciones de aproximación local producen matrices dispersas que representan mejoras computacionales al mismo tiempo que mejoran los problemas numéricos, el mal condicionamiento y la precisión de los resultados.
4. Método de colocación local con RBF
Las aproximaciones locales son aquellas que se aplican en pequenas subregiones o subdominios del problema, en lugar de aplicarse a todo el dominio completo. Todas las formulaciones de colocación global RBF explicadas anteriormente: la formulation asimétrica de Kansa, la hermítica y la de soluciones particulares aproximadas, pueden aplicarse también de manera local. Para obtener una formulation local a partir de una aproximación global, se realiza una partición del conjunto total de nodos del dominio en subconjuntos mas pequenos traslapados o esténciles. Cada esténcil puede contener diferentes tipos de nodos como se observa en la figura 1.
Por ejemplo, si se utiliza la formulación de soluciones particulares, en cada uno de los nodos de un esténcil es posible aplicar una aproximación de la forma definida por la ecuación 14, dando lugar a un sistema de la forma,
Resolviendo este sistema pueden obtenerse los valores de los coeficientes α en términos de los valores nodales de u en cada esténcil,
Observe que en este caso es posible usar la inversa de la matriz dado que el tamaño del sistema es reducido porque se trata de un esquema local y las ecuaciones de un solo esténcil con un número limitado de nodos, diferente del esquema global donde el número total de nodos es mucho mayor. Una vez encontrados los coeficientes, se usa la ecuación 14 para expresar el valor de u(x) en cualquier nodo del esténcil en términos de los valores de u en los nodos que definen el esténcil (valores nodales de u), vectorialmente puede escribirse,
De manera similar es posible aproximar localmente las derivadas o cualquier otro operador diferencial lineal en cada esténcil, en un punto dado, a partir de las ecuaciones 14 y 21. Por ejemplo, las derivadas parciales de orden k respecto a x¡ pueden aproximarse como:
Observe, que la ecuación 22 es en realidad una cuadratura diferencial local, dado que la derivada en un punto se calcula en términos de los valores nodales u en los nodos vecinos a dicho punto en cada esténcil. Por esta razón algunos autores han denominado a este método como diferencias finitas generalizadas con RBF (Fornberg y Lehto, 2011). De la misma forma, para obtener la aproximación local del problema definido en la ecuación 11, se aplica la ecuación diferencial en un nodo seleccionado de cada esténcil y la condition de frontera en cada nodo de frontera, para obtener las expresiones discretas,
donde,
En el ensamblaje final, las aproximaciones ecuaciones 23 y 24 se aplican a cada esténcil y se estructura un sistema de ecuaciones acopladas con una matriz de coeficientes dispersa, dado que los esténciles al traslaparse comparten entre si un determinado número de nodos.
Se presentan a continuación dos problemas resueltos numericamente mediante métodos locales RBF. Las soluciones obtenidas serán comparadas con soluciones exactas o con soluciones presentadas publicadas conocidas, para propósitos de validación o comparación (benchmarking numérico). En el presente trabajo no se realizaron estudios experimentales de laboratorio.
5. Caso ejemplo 1: Flujo electro-osmótico
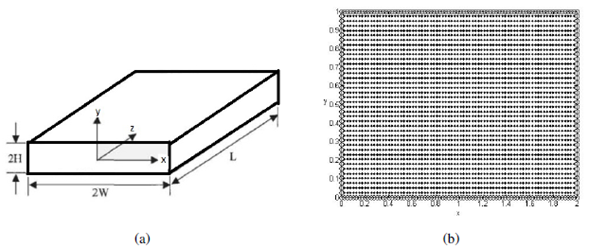
Se presenta el problema de flujo electro-osmótico newtoniano en estado estacionario completamente desarrollado, impulsado por un gradiente de presión en un microcanal. Según (Sadeghi, Azari, y Chakraborty, 2017), la pared del canal está sujeta a un potencial constante y el fluido contiene una solución ideal de una sal completamente disociada. El dominio computacional se presenta en la figura 2(a) como la región bidimensional sombreada, junto con la distribution de nodos (figura 2(b)) El modelado de los flujos electro-osmóticos en micro y nano-canales es importante para comprender el transporte de agua y protones en las membranas de electrolitos poliméricos (PEM) que tienen nano-canales en su estructura (Berg y Ladipo, 2009). Se ha demostrado que una alternativa para describir el flujo en estos pequenos canales es la ecuación de Poisson-Boltzmann (PB) acoplada al flujo de Stokes (Berg y Ladipo, 2009). Las ecuaciones de distribution de potencial eléctrico y de flujo hidrodinámico desarrollado en 2-D, impulsado por un gradiente de presión constante a lo largo del canal, son:
La ecuación de Poisson-Boltzmann (PB) adimensional,
donde K = H/λ
D
es el parámetro de Debye-Huckel, λ
D
=
la longitud de Debye length y las variables adimensionales para el potencial
y la position x* =
, y* =
. Los parámetros son: n
0
la concentration de iones,Z la valencia de las especies ionicas, ε permitividad, e la carga de protones,k
B la constante de Boltzmann, T temperatura.
Las ecuaciones de continuidad y momentum para el flujo electro-osmótico,
donde p es la presión, t el tensor de esfuerzos, u la velocidad, F = ρ e E el vector de fuerza donde E denota el campo eléctrico y p e la densidad de carga. Considerando flujo axial totalmente desarrollado con un vector de velocidad u =(0,0,u z (x,y)), las ecuaciones de momentum, en forma adimensional, se reducen a:
donde x* = x/H, y* = y/H, u* = u z /u HS , u HS = -εζE z /μ es la maxima velocidad electro-osmótica posible llamada velocidad de Helmholtz-Smoluchowski, ζ el zeta potencial, n es la viscosidad y Γ = u PD /u HS la relation de la escala de velocidad con u PD = -H 2 (∂p/∂z)/2μ, (Sadeghi, Kazemi, y Saidi, 2013).
Aquí ζ* es el potencial adimensional externo y α = W/H la relation de aspecto del canal.
El problema definido por las ecuaciones 28-33, se ha resuelto utilizando la formulation local del método MAPS, aproximando las variables del problema u* y ψ* mediante una expansión similar a la ecuación 14 en cada nodo de los esténciles. Esto en notation matricial según la ecuación 21 se expresa como:
con Û = (û (x, ξ 1 ),… (û (x, ξ N )donde û son las soluciónes particulares de
El operador diferencial L (ecuación 13) se ha elegido en este caso como el operador de Laplace ∇2, cuya solución particular radial asociada (ecuación 15) esta dada por(Chen y cols., 2012),
correspondiente a la función radial multicuádrica Φ(r¡)=
Después de substituir las ecuaciones 34 en el sistema de ecuaciones 28-33 en un nodo de cada esténcil se obtiene un sistema no-lineal de ecuaciones que puede resolverse mediante el método de Newton Raphson. La figura 3 muestra algunos resultados representativos correspondientes a diferentes valores de los parámetros del flujo electro-osmótico, obtenidos con N = 3200 nodos uniformemente distribuidos (figura 2(b)), utilizando un código elaborado en Python, con un procesador Intel™ Xeon™ E-2124, 3.5 GHz, 16 GB RAM. Los tiempos de computo representativos dependiendo del número de nodos se presentan en la tabla 2
Figura 3 Distribuciones de potencial y velocidad adimensionales para el flujo electro-osmótico con N = 3200 nodos
Tabla 2 Tiempo típico de CPU para el problema electro-osmotico
| Nodos | Incognitas (grados de libertad) | Tiempo de CPU(s) |
|---|---|---|
| 256 | 512 | 305 |
| 400 | 800 | 1210 |
| 1600 | 3200 | 3400 |
| 2500 | 5000 | 7600 |
Los fuertes efectos en las esquinas debido a las cargas superficiales son evidentes, produciendo una zona eléctricamente activa cerca de la pared del canal y una pasiva en la parte central del canal, como también lo muestran Dongqing et al. (Li, 2004). Se espera que el potencial en las esquinas provoque una fuerte resistencia al flujo. Los perfiles potenciales en la línea y = 0.5 con el efecto en las esquinas se detallan en la figura 1S. Es importante mencionar que la variación de K equivale a un cambio de densidad iónica en condiciones neutrales (n 0) o un cambio de permitividad (ε), ya que otros parámetros se fijan como constantes.
La figura 2S muestra la distribution de velocidad para diferentes valores de la relation de escala de velocidad r. El flujo puramente electro- osmótico. Mientras que en el caso r = 1, el perfil de velocidad es el resultado de la superposition de efectos electro- osmótico y de presión. Cuando Γ = -1, el gradiente de presión es adverso al flujo electro-osmótico, de manera similar para Γ = -1.5. A medida que aumenta la magnitud de la relation de escala de velocidad negativa, se obtiene un reflujo en la zona central del conducto mientras que se producen valores de velocidad positivos hacia las paredes. Por lo tanto, el efecto electro- osmótico produce un perfil de velocidad mas plano que el observado comúnmente en los flujos impulsados por presión.
Finalmente, la figura 4 muestra el error cuadrático medio para el potencial, que se obtiene al comparar la solución numérica obtenida con diferentes formulaciones con la solución exacta del problema presentada en (Sadeghi y cols., 2013). Se observa que aunque todas las formulaciones convergen al aumentar el número de nodos, la formulation local MAPS produce mayor exactitud, seguida de la formulation global MAPS que produce resultados muy similares a la estrategia local de Hermite, y la formulation de Kansa aunque es la mas sencilla de plantear, produce casi el doble del error especialmente para un número de nodos menor a 500.
6. Caso ejemplo 2: Problema de electrohilado
Se presenta a continuación la solución por colocación radial local directa asimétrica, de un problema de electro hilado. La solución por RBF de este tipo de problemas es hasta la fecha original e inédita, por lo cual es un problema adecuado para probar la efectividad de los métodos expuestos. La finalidad de este ejemplo es mostrar que los métodos RBF pueden extenderse a sistemas de ecuaciones ordinarias algebraico diferenciales no lineales.
Como se mencionó en la sección 1, los métodos de colocación pueden adaptarse con facilidad a cualquier número de dimensiones dado que se aplica la misma función RBF y solo cambia la definición de la norma o distancia dependiendo de la dimensionalidad del problema.
Aunque la formulación local de los métodos con RBF se suele aplicar a ecuaciones diferenciales parciales, no existe ningún impedimento para aplicarlo también a complejos sistemas de ecuaciones diferenciales ordinarias no lineales. De hecho, en los inicios del método, Viktor Popov (Popov, 1996) lo propuso para problemas de una dimensión divididos en subdominios para obtener un sistema disperso. En otros trabajos mas recientes Dehghan (Dehghan y Nikpour, 2013) resuelve sistemas de ecuaciones ordinarias de segundo orden, por su importancia en ingenieria, física y biologia, problemas lineales de analisis estructural unidimensionales (Tiago y Leitao, 2006), e inclusive en (Dehghan y Nikpour, 2013) se resuelven sistemas mas complejos de ecuaciones unidimensionales de Schrodinger-Gross-Pitaevskii aplicando técnicas locales RBF.
El electrohilado es una técnica ampliamente utilizada para desarrollar nanomateriales con estructuras fibrilares, lo cual permite implementarlos en diferentes aplicaciones como medios filtrantes, tejidos médicos, baterías, entre otras. El proceso funciona a traves una diferencia de potencial aplicada por una fuente de alimentación de alto voltaje a una solución polimérica con una determinada polaridad y propiedades viscoelaísticas. Esta solución, normalmente almacenada en una jeringa con aguja, es atraída por una placa metálica de polaridad opuesta liberando un chorro hacia la placa metálica donde se recoge, como lo ilustra la figura 5. El modelo matemático para este problema está compuesto por las siguientes
ecuaciones algebraico diferenciales (J.Feng, 2002; Carroll y Joo, 2006):
Ecuación de continuidad:
Ecuación de conservation de la carga:
Balance de momentum:
Ecuación de campo eléctrico:
donde R es el radio y v, la velocidad del hilo de polímero, X = L/R 0 es una coordenada adimensional, L es la distancia entre la aguja y el colector, R0 el radio inicial del hilo, E el campo eléctrico, σ la carga eléctrica, T p es el esfuerzo de tensión. La variable independiente z es la distancia medida desde la salida de la aguja, y la derivada respecto a z se denota por el símbolo de prima en cada variable. Los parámetros adimensionales del modelo se resumen en la tabla 3
Tabla 3 Parámetros adimensionales del modelo, ε : permitividad eléctrica del polímeros: 
permitividad del vacío, η
p viscosidad del polímero, η
0 viscosidad a rapidez de deformación núla ,λ tiempo de relajamiento,v0 velocidad en la boqúilla,E0 campo eléctrico en la boqúilla,g gravedad, K conductividad eléctrica de la fibra
El esfúerzo de tensioín Tp,
puede calcularse a partir de cualquier modelo reológico viscoelástico, particularmente en este ejemplo se ha utilizado el modelo de Giesekus (J. J.Feng, 2003; Bird, Armstrong, y Hassager, 1987):
donde T prr y T pzz representan los esfuerzos normales en la fibra radiales y axiales respectivamente, y α es el factor de movilidad asociado con el arrastre hidrodinámico en las moléculas de polímero. El modelo de Giesekus asume que las cadenas de moleculas de polímero son relativamente grandes causando elasticidad. Además, este modelo incluye el tiempo de retardo para evitar la región de ley de potencias donde la viscosidad es proporcional a la inversa de la velocidad de deformación. Otros modelos reológicos alternativos han sido utilizados en este ejemplo con propositos de comparación, como el modelo FENE-P (Bird y cols., 1987).A diferencia del modelo de Giesekus, el modelo FENE-P considera una ex-tensibilidad finita de las cadenas de polímero pero no considera el tiempo de retardo en la extensibilidad (Carroll y Joo, 2006). Las condiciones de frontera del problema están dadas por:
Para la solución numérica se utiliza el método de Kansa de colocación directa para cada una de las variables en las ecuaciones 37-43, con la función radial multicuádrica (tabla 1) sin utilizar polinomios adicionales en la expansión. Además, se recurre a una formulación local como la presentada en las ecuaciones 22-24 para aproximar las derivadas y los operadores diferenciales de las ecuaciones del modelo y las condiciones de frontera. En todas las aproximaciones locales se utilizan esténciles traslapados de 3 nodos como se ilustra en la figura 3S
Es importante mencionar que para este ejemplo se opta por el método de colocación local de Kansa, debido a que una formulation de Hermite no puede aplicarse aquí, ya que el problema no está planteado en términos de operadores diferenciales lineales auto-adjuntos, sino que están inmersos en términos no-lineales e implícitos de un sistema algebraico diferencial no trivial. Debe tenerse en cuenta, que no todas las formulaciones RBF son aplicables a todo tipo de problemas.
El sistema final de ecuaciones no lineales resultante, se resuelve mediante un método de Newton-Raphson con paso variable y convergencia global. El número de nodos y esténciles utilizados es N = 1200. Los resultados obtenidos se compararon con el solucionador de problemas de valor de frontera solvebvp de la biblioteca de SciPy de Python basado en el método implícito de Shampine (Shampine, Muir, y Xu, 2006), y con los resultados numéricos presentados por Carroll (Carroll y Joo, 2006) y Feng (J. Feng, 2002). Los resultados se obtuvieron con un procesador Intel™ Xeon™ E-2124, 3.5 GHz, 16 GB RAM. Los tiempos de computo representativos dependiendo del número de nodos se presentan en la tabla 4
En la figura 6 se presenta la solución numérica comparada para 3 modelos geológicos: el modelo de Giesekus, FENE-P y el modelo Oldroyd-B. La solución obtenida por RBF es muy precisa en comparación con la solución del solucionador de Python y concuerda bien con los resultados presentados en (J. J.Feng, 2003). Confirmando lo mencionado en la literatura, todos los modelos muestran que el radio disminuye principalmente en la boquilla, pero aguas abajo el adelgazamiento es más lento (Hohman, Shin, Rutledge, y Brenner, 2001). Este adelgazamiento se produce considerablemente rápido en una región estrecha, por lo que el sistema de ecuaciones se vuelve rígido (stiff) como afirma Russo (Russo, Capasso, Nicosia, y Romano, 2016). Los modelos Newtoniano y Oldroyd-B establecen dos límites. Cada modelo puede asociarse con un tamaño de molécula diferente, lo que a su vez provoca un comportamiento geológico particular. La precisión del método de colocación local RBF se puede corroborar a traves de los resultados que se muestran en la figura 7, donde la densidad de carga superficial a y el campo eléctrico E se grafican y comparan con los resultados obtenidos por Feng (J. J. Feng, 2003). La rigidez de las ecuaciones mencionadas anteriormente, se confirma porque aparece un pico estrecho en una pequeña región en ambas curvas. Tanto a como E suben cerca de la boquilla, forman un pico y luego disminuyen corriente abajo. Esto aparece porque la sección transversal de la fibra disminuye considerablemente. La reducción del transporte de cargas en la superficie de la fibra provoca una acumulación de cargas que incrementa las variables. Después de ese punto, los fenómenos de conservation de carga y advección llevan más cargas provocando una disminución lenta de las variables. Cabe mencionar que experimentalmente, un fenómeno similar puede observarse presente debido a la tensión superficial del fluido cuando se aplica un alto voltaje. Esta fuerza, evita que el hilo sea expulsado de la jeringa, generando una gota esférica. Posteriormente, cuando la fuerza de atracción supere la tensión superficial, la gota se convertira en un cono de Taylor, generando pequenas fibras. Dado que la gota esférica impide el flujo, las cargas superficiales se acumularan aquí, aumentando σ. Sin embargo, cuando se expulsa el hilo, las cargas se disiparan a lo largo de la superficie del chorro (Haider, Haider, y Kang, 2018).
Figura 6 Radio de la fibra con el modelo newtoniano, FENE-P, Giesekus y Oldroyd-B, comparado con los resultados publicados.
7. Conclusiones
El método de funciones de base radial, en sus diferentes formulaciones, ha probado ser una técnica de aproximación simple, versátil, robusta y potente para resolver problemas de fenómenos de transporte basados en modelos de ecuaciones diferenciales. Particularmente, en los ejemplos analizados en este trabajo, el método ha sido efectivo para resolver ecuaciones de problemas acoplados no lineales de interés en ingeniería, que involucran fluidos y cargas eléctricas. Además, se ha logrado extender la aplicación de los métodos locales RBF a problemas acoplados, no lineales y sistemas algebraico-diferenciales, como se ha demostrado en los problemas electro-osmóticos y electrohilado presentados. Las funciones de base radial tienen un amplio rango de aplicación, como interpolantes de datos dispersos en espacios multidimensionales y como funciones base para la aproximación de la solución de modelos basados en ecuaciones diferenciales, tema que en el cual se centra el presente trabajo. Todas las técnicas basadas en RBF pueden aplicarse directamente para problemas en 1, 2 o n dimensiones, tanto en su formulation global como en su formulation local. Además, las formulaciones de colocación de Hermite permiten construir aproximaciones conservativas capaces de cumplir exactamente el operador diferencial en un conjunto de puntos, mientras que la técnica de soluciones particulares produce esquemas donde las variables se expresan como una superposición lineal de soluciones particulares de la ecuación diferencial original. Estas características, hacen de las RBF una potente técnica que describe la física de los problemas y no unicamente los valores numéricos de las variables, como ocurre en las interpolaciones no conservativas que no tienen en cuenta el operador diferencial al construir las aproximaciones. Finalmente, una lectura detallada de las referencias incluidas en este trabajo, ilustra como se ha expandido el uso de las técnicas presentadas a diversos problemas de dinámica de fluidos y fenómenos de transporte en general, así como su potencial de aplicaciones futuras.
