Determinación de los parámetros críticos (β, γ, Tc) usando el método de Kouvel-Fisher

La aplicación de este método a la muestra MnFe se ilustra a continuación. En la figura 1 se presentan sus correspondientes planos de Arrott-Kouvel trazados a partir de un conjunto de datos (no ilustrados aquí) de isotermas de magnetización (M vs. H) para un conjunto de 55 temperaturas diferentes incluyendo la temperatura crítica T _C . Esos planos muestran curvaturas intrínsecas, las cuales indican que esa muestra, cuyo estado estructural es policristalino, tiene algún grado de heterogeneidad. Curvaturas intrínsecas, pero más fuertes, se observan también en los planos de Arrott-Kouvel de la muestra FeCr, cuyo estado estructural es amorfo como se explicó anteriormente. Dichas curvaturas dificultan la determinación de T _C con buena precisión. A pesar de esto, en un intento por determinar los parámetros críticos (β, γ, T_C) de dichas muestras, aquí se utilizaron los datos de M ₀ (T) y de X ^-1(T obtenidos desde esos planos para ser tratados según el método de Kouvel-Fisher (Ecuaciones 5 y 6).

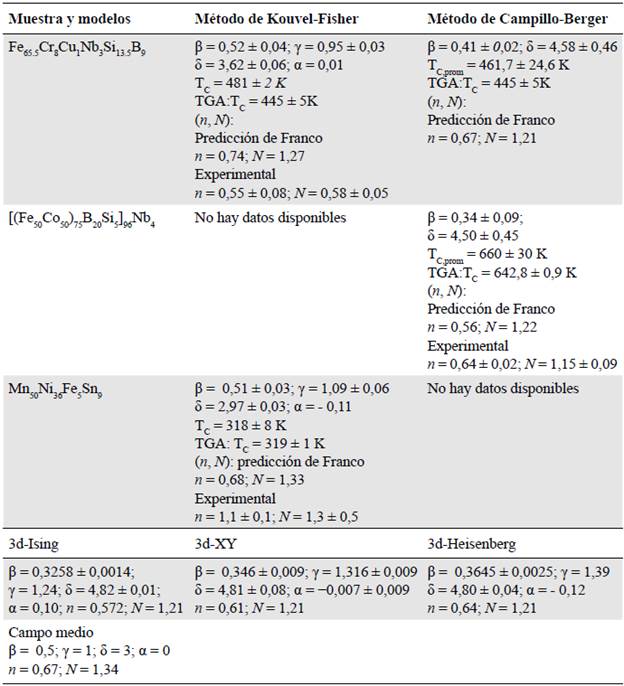
A partir de los datos M ₀ (T) y X ^-1(T correspondientes a ambas muestras se obtuvieron los datos de M ₀ (dM ₀ /dT) ^-1 y X _o ^-1(dX _o ^-1/dT)^-1 para las diferentes temperaturas de trabajo, los cuales se grafican en la figura 2. Los valores de (β, γ, T _C ) se determinaron a partir de un ajuste de mínimos cuadrados del conjunto de datos de la figura 2 y se presentan en la tabla 1. Ese conjunto de datos se limitó al intervalo de campo 1 < H < 10 kOe, para el cual los planos de Arrott-Kouvel exhiben un comportamiento lineal con un factor R-cuadrado del orden de 0,99 y 0,98 para MnFe y FeCr, respectivamente. Los valores para (β, γ) de ambas muestras fueron cercanos a los de la clase de universalidad de campo medio con interacciones de largo alcance. Es oportuno comentar que existe una pequeña diferencia de temperatura entre T_C, determinada a partir de M _g (T) y de X ^-1 (T) en la ecuación (5), y la determinada de X ^-1(T) dada por la ecuación (6), como se puede observar en la figura 2. Este hecho refleja la heterogeneidad de las muestras y es compatible con las curvaturas intrínsecas de las gráficas de Arrott-Kouvel.

Figura 1 Planos de Arrott-Kouvel, M ² Vs. (H/M) para MnFe 

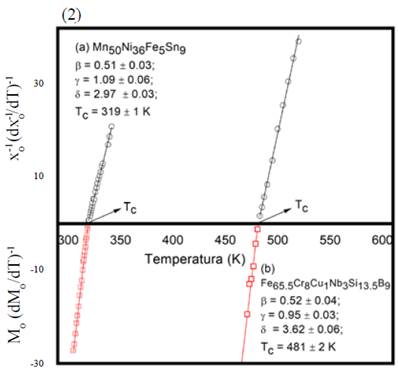
Figura 2 Parámetros críticos (β, γ, Tc) para a) MnFe y b) FeCr. Los símbolos (, o) corresponden a datos de M _o (T) y x ^-1 (T) respectivamente. 

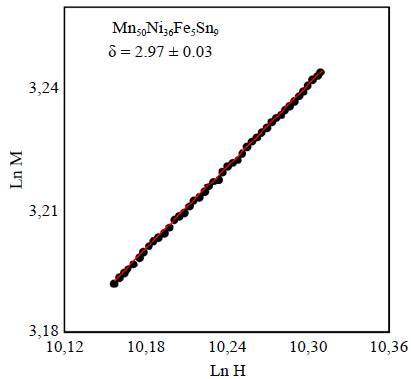
Por otro lado, el valor de δ para cada una de las muestras se determinó utilizando una gráfica Ln M Vs. Ln H para T = T_C. Ese procedimiento se ilustra en la figura 3 para MnFe; se observa que los datos Ln M Vs. Ln H siguen una buena relación lineal. Un comportamiento similar se observó en la muestra FeCr. El valor de δ determinado de esta manera se presenta en la tabla 1 para ambas muestras. Nótese que el valor de 5 se encuentra en el rango de los observados experimentalmente en sistemas FM (^{Collins, 1989}). Además, es coherente con el valor obtenido independientemente al usar la relación de escala δ = 1 + y/β de ^{Widom (1965)}. Por otro lado, utilizando los valores anteriores para (β, γ) en la relación de escala α = 2(1 - β) - y de ^{Rushbrooke (1963)}, se obtuvo el valor del exponente a (Tabla 1). La confiabilidad de los anteriores parámetros críticos se examinó a la luz de la hipótesis de escala sistematizada por ^{Griffiths (1967)}. Dicha hipótesis establece que para un sistema FM, el escalamiento de su ecuación de estado se puede expresar como,

donde f _± es una función de escala, los signos más y menos corresponden a temperaturas por encima y por debajo de T _C , respectivamente, y |t | = (T-T _C )/T _C , de tal manera que una gráfica de (M / |t | ^β ) Vs. (H / |t |^(β + ^γ)) en la región crítica dará dos curvas diferentes, una para T > T _C y la otra para T < T_C. Utilizando los valores de (β, γ, T_C) para ambas muestras, se verificó dicha hipótesis de escala para varias temperaturas en el intervalo |t | ≤ 2x10^-2 y 1 ≤ H ≤ 10 kOe, y se encontró que los valores de (β, γ) cumplían satisfactoriamente la hipótesis de escala. Esto se ilustra en la figura 4 para la muestra MnFe. Allí se observa que la variable dependiente escalada (M/|t | ^β ) se expande por lo menos tres órdenes de magnitud y que los datos escalados colapsan bien en dos ramas, una para T > T _C (región paramagnética) y otra para T < T _C (región ferromagnética). En FeCr, los correspondientes datos escalados también presentaron un colapso en dos ramas, que era el esperado de acuerdo a la hipótesis de escala, e indicaba que los valores obtenidos para los exponentes críticos eran confiables dentro del error experimental.

Figura 4 Verificación de la hipótesis de escala de la ecuación de estado magnética para (β, γ) para MnFe 

Figura 3  Ln M vs. Ln H a T = T _C para MnFe, de donde se obtuvo el valor de δ. La línea en color rojo corresponde a un ajuste de los datos por el método de mínimos cuadrados. 

Determinación de los parámetros críticos (β, δ, T _C , _prom ) usando el método de ^{Campillo et al. (2001)}

Este método se aplicó a las muestras de FeCr y FeCo. Los datos experimentales y los numéricos obtenidos a través del ajuste de los datos experimentales usando la ecuación (7) para la M(T) de la muestra FeCr, la cual corresponde a este método, se presentan en la figura 5, donde se observa que las curvas de magnetización disminuyen con el aumento de la temperatura y tienden a cero a través de una pequeña cola. Esa caída de tipo cola se debe tanto a la heterogeneidad magnética de la muestra como al efecto del campo magnético de destruir la transición de fase FM-PM. Resultados similares (no se muestran aquí) se obtuvieron para la muestra de FeCo. Los valores obtenidos por este método para β en función del campo magnético en las dos muestras se ilustran en la figura 6a, b, respectivamente. Nótese que β exhibe primero una dependencia notable del campo hasta cierto valor de campo H _pequeño (del orden de 1 kOe en cada muestra). Para H > 1 kOe esa dependencia se vuelve muy débil, lo que resulta en un comportamiento casi constante de ß en función del campo. En el marco de la precisión experimental, el comportamiento de H > 1 küe es consistente con el supuesto teórico involucrado en la deducción de la ecuación (7) de que ß no depende del campo magnético, aunque el comportamiento para H < 1 küe se desvió de ese supuesto, lo que podría estar asociado con el hecho de que cuando un sistema FM está expuesto a un campo magnético externo, sus dominios no pueden alinearse completamente a lo largo del campo si el campo aplicado es pequeño. Como lo estipuló por primera vez ^{Kouvel (1957)}, y lo reiteró más tarde^{Aharoni (1986)}, una condición esencial para la determinación de exponentes críticos estáticos en sistemas ferromagnéticos es que todos sus dominios estén alineados con el campo magnético aplicado. Siguiendo este supuesto, el exponente ß se determinó extrapolando las curvas β Vs. H desde los campos altos (H > 1 kOe, región de saturación) hasta el campo cero. Los valores del exponente crítico β obtenidos de esta manera para las diferentes muestras se dan en la tabla 1, junto con los valores para δ obtenidos utilizando la ecuación (8). Además, los valores de (β, γ, δ, α) para Fe, Co, y los modelos de Ising, XY, Heisenberg y de campo medio, se incluyeron también en la tabla para comparación. La temperatura promedio T _C , _prom , que en el presente caso correspondió a la temperatura de Curie T _C , es otro parámetro obtenido a partir del ajuste de las curvas de magnetización usando la ecuación (7), cuyos valores se incluyen en la tabla 1.

Tabla 1 Valores para los exponentes (ß, γ, δ, α), temperaturas críticas y exponentes (n, N) 

Figura 5 Datos experimentales (símbolos) y ajustados numéricamente (líneas en color rojo) usando la ecuación (7) para M Vs. T en diferentes campos para FeCr 

Figura 6 β Vs. H para a) FeCr y b) FeCo. Las líneas (a) continua y (b) en trazos representan el valor promedio de β obtenido para H > 1 kOe. 

Los valores obtenidos para (β, γ, δ) con los dos métodos indican que FeCo pertenece a la clase de universalidad 3d-XY con interacciones de corto alcance, en tanto que FeCr y MnFe pertenecen a la clase de universalidad de campo medio con interacciones de largo alcance. La consistencia entre los valores determinados para (β, γ, δ) por ambos métodos es de especial interés debido a que indica que son confiables, lo que ya se discutió la luz de la hipótesis de escala.

Exponentes críticos y el efecto magneto-calórico

El efecto magneto-calórico de cada muestra se determinó mediante la cuantificación del cambio de entropía magnética isotérmica ΔS_M debido a la aplicación del campo magnético usando la ecuación (9) para diferentes intervalos de campo magnético. En la figura 7 se presenta un conjunto de curvas (-ΔS _max ) Vs. T para la muestra de FeCo obtenido como se explicó anteriormente. Cada curva exhibió un máximo localizado en la misma temperatura T _(-ΔSmax) . Cada una de las curvas (-ΔS _max ) Vs. T de las otras muestras también exhibió un máximo, el cual, como en la muestra de FeCo, se localizó a la misma temperature T ₍ - _ΔSmax) , la cual difirió para cada muestra. En las tres muestras, la temperatura T ₍ - _ΔSmax) cayó en el rango de su correspondiente T _C . Este hecho sugiere que el máximo en las curvas (-AS ) Vs. T es una manifestación de la transición de fase continua FM que ocurre en la temperatura crítica T _C en esas muestras y, además, se enmarca en los argumentos teóricos de ^{Franco et al. (2009)}. Por otro lado, la amplitud del máximo (-ΔSmax) evaluada en T_(-ASmax) para АH = 10 kOe en FeCo, FeCr y MnFe fue de (0,6; 0,75; 0,5) Jkg^-1K^-1, respectivamente. Otra característica observada en las curvas (-ΔS_max) Vs. T fue que el máximo (-ΔS_max) era más amplio en las muestras de FeCo y FeCr que en la de MnFe. A partir de las curvas (-ΔS_max) Vs. T se obtuvo el valor de RCP de cada muestra, calculado según lo estipulado por ^{Tishin & Spichkin (2003)} como RCP = (-ΔS _max ) x δT _FWHM, donde (-ΔS_max) es la máxima disminución de entropía con respecto a la temperatura y 5T_FWHM es el ancho evaluado a la altura media del máximo de entropía. Los valores para RCP obtenidos de esta manera se presentan en la tabla 2: los de FeCo, FeCr y MnFe fueron (57,4; 56,6; 25,1) Jkg^-1, respectivamente. Las dos primeras muestras, que presentaron la mayor RCP, cumplían mejor con el compromiso entre la magnitud del cambio de entropía magnética y el ancho del máximo requerido para que un material se considere promisorio y pueda aplicarse como uno funcional en la tecnología de refrigeración magnética siguiendo los argumentos teóricos de ^{Wood & Potter (1985)}. Sin embargo, dichos valores para RCP son menores en comparación con los de otras aleaciones como Gd₅Ge₂Si₂ (200 Jkg-¹ a H = 5T) (^{Provenzano et al., 2004}), pero del mismo orden de magnitud para las aleaciones Heusler Co₂Ti₀.₇₅Sn_1.25, (71 Jkg-¹ a H = 5 T), y Co₂Ti_0.5Sn_1.5, (45,2 Jkg-¹ a H = 5 T) (^{Remya et al., 2021}), Mn_{39 5}Fe_8.5Ni₄₁Sn₁₁ y Mn_{37 5}Fe_10.5Ni₄₁Sn₁₁ (40,2 Jkg-¹ y 36,7 Jkg-¹ a H = 1,4 T) (^{Ghosh et al., 2021}).

Figura 7 Ilustración de (-AS ) Vs. T debido a la aplicación del campo magnético en FeCo 

A partir de las gráficas logarítmicas de (- ΔS_M) y la RCP en función del campo magnético (proceso de linealización no ilustrado aquí), se determinaron los valores para los exponentes n y N, respectivamente (Tabla 2). Es de particular interés comparar dichos valores con los de n y N previstos por las ecuaciones (10) y (12), respectivamente. Para la muestra de FeCo, la evaluación de la ecuación (12) usando sus correspondientes valores de (β, δ) y los del modelo 3d-XY predijo un valor de n razonablemente comparable con el determinado experimentalmente a partir de las curvas (- ΔS _M ) Vs. T. Este no fue el caso para las otras muestras, en las que el valor de n previsto por esa ecuación se desvió considerablemente de aquel determinado experimentalmente. Por otro lado, para las muestras de FeCo y MnFe, el uso de la ecuación (12) con sus correspondientes valores de δ predijo un valor de N muy comparable con el determinado experimentalmente a partir de las curvas RCP Vs. T, pero no así para la muestra de FeCr, en la que se registró un notable desvío entre el valor de N previsto y el determinado experimentalmente.

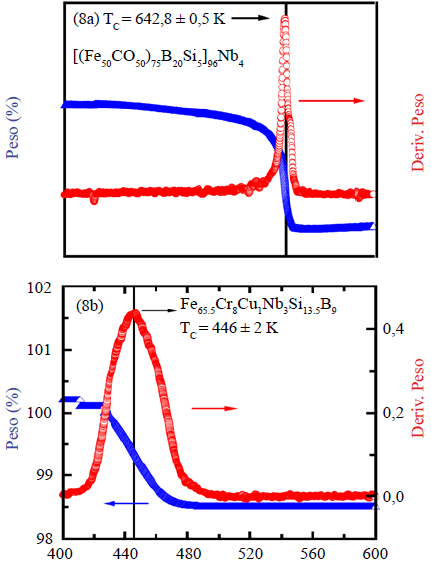
Análisis termogravimétrico TGA y temperatura crítica

La figura 8a, b (curvas en color azul) ilustra los termogramas magnéticos de las muestras FeCo y FeCr, respectivamente. Estos se obtuvieron al incrementar la temperatura ambiente de las muestras hasta una alta temperatura a una velocidad de 10 °C/min en una atmósfera de gas de nitrógeno de grado analítico para un campo magnético externo fijo de H = 2 Oe. Las dos muestras presentaron una visible pérdida de peso que se extendió a través de una pequeña cola a medida que la temperatura aumentó. Ese comportamiento es similar a la disminución de tipo cola observada en las curvas de magnetización en las proximidades de T _C discutida previamente. Las curvas en color rojo de las anteriores figuras corresponden a la derivada térmica de los termogramas. Cada una de esas derivadas exhibe un máximo relativamente estrecho y bien definido en una cierta temperatura de T = T _MAX-TGA . En contraste con esos máximos estrechos y bien definidos, un máximo débil en se encontró en la derivada térmica del termograma de la muestra de MnFe. Es interesante anotar que cada valor de T_MAX-TGA coincidió razonablemente bien (dentro del error experimental) con el correspondiente valor de T _C en campo cero obtenido mediante los métodos de ^{Kouvel & Fisher (1964)} y ^{Campillo et al. (2001)}. Los máximos observados en esas derivadas son indicios de una transición de fase FM-PM en la proximidad de T _C , y ayudan a determinar esta temperatura. Ello se justificó al considerar la coincidencia entre y T_C, y porque los sensores de temperatura empleados en los experimentos de magnetización y TGA fueron previamente calibrados. Por otro lado, es factible que el debilitamiento del máximo de la derivada térmica del termograma en la muestra de MnFe no se deba completamente a la destrucción de la transición de fase FM-PM causada por el campo magnético, dado que este campo es muy pequeño, del orden de 2 Oe. Una posible explicación de este comportamiento es que el ordenamiento ferromagnético en esta muestra fue incipiente o débil, lo cual es coherente con estudios de espectroscopia Mössbauer (^{Saccone, 2021}) hechos en esa aleación, que mostraron dobletes de interacción cuadrupolar y no sextetos magnéticos bien definidos, e indica que el magnetismo en esa aleación se puede asociar con un acoplamiento ferromagnético entre los elementos de Mn, Ni y Sn.

Tabla 2 Comparación de (-AS_M) y (RCP) para las aleaciones bajo estudio 

Figura 8 Termograma magnético para a) FeCo y b) FeCr 

Exponentes críticos y algunas interacciones magnéticas

Anisotropía magnética y efecto Hall extraordinario. Como se mencionó en la introducción, un aspecto básico de los exponentes críticos es su dependencia del rango de las interacciones magnéticas, y si son de corto o largo alcance. Por ello, el conocimiento sobre la manifestación de las interacciones magnéticas es esencial para entender los valores asumidos por los exponentes críticos. Entre las diferentes interacciones magnéticas, aquí se abordaron las de intercambio, las de espín-orbita y las de Ruderman-Kittel-Kasuya-Yosida (RKKY) mediante el análisis de los valores asumidos por la temperatura de Curie T _C , de los datos de anisotropía y del efecto Hall, respectivamente, obtenidos experimentalmente. La interacción de intercambio, que es de corto alcance, está íntimamente relacionada con la T _C , y la interacción espín-orbita, también de corto alcance, está en el corazón tanto del efecto de anisotropía magnética como del efecto Hall extraordinario. La interacción RKKY, en el camino entre el mediano y el largo alcance, cumple un papel importante en el acoplamiento entre momentos localizados vía los electrones de conducción en metales; es decir, está relacionada con la densidad de los portadores de carga n _c . Con relación a la interacción de intercambio, es importante tener en cuente que los valores altos de T _C implican interacciones de intercambio fuertes. Así, a partir de la proporcionalidad entre dicha interacción y la T _C (ver los valores de T _C en la (tabla 1), se pudo establecer que, en el caso presente, la interacción de intercambio fue comparativamente más fuerte en FeCo que en FeCr y MnFe, siendo más débil en MnFe. La interacción espín-orbita siguió un comportamiento similar a la interacción de intercambio en dichas aleaciones, como se explica a continuación.

Los resultados para los ciclos de histéresis axial y transversal en función del campo magnético obtenidos a temperatura ambiente para FeCo y FeCr se ilustran en la figura 9 a, b, respectivamente, para su comparación. En la figura 10 a, b, c se presentan las curvas del efecto Hall en función del campo magnético obtenidas a temperatura ambiente para FeCo, FeCr, y MnFe. Los lazos de histéresis exhibieron una clara anisotropía magnética, pues a lo largo de la dirección longitudinal es más fácil magnetizar las muestras que en la dirección transversal. Una estimación de la anisotropía magnética se puede obtener determinando el área incluida entre las curvas de magnetización a lo largo de esas direcciones. En la figura 9 a, b se observa que el área entre los lazos de histéresis longitudinal y transversal fue mayor en FeCo que en FeCr y, así, la anisotropía magnética fue mayor en FeCo que en FeCr. El ciclo de histéresis (no se muestra aquí) para MnFe también presentó anisotropía magnética, siendo esta levemente menor que la de Fe₆₅.₅Cr₈Cu₁Nb₃Si_13.5B₉ y la de FeCo. Este hecho sugiere que la interacción espín-órbita fue comparativamente más fuerte en FeCo que en FeCr y MnFe. Por otro lado, tanto la magnetización transversal como las curvas de efecto Hall muestran, primero, una dependencia lineal del campo magnético y su paso por un cambio de pendiente en un cierto valor de campo, H _S , antes de alcanzar, finalmente, la región de saturación en campos magnéticos altos. H _S es el campo que marca el inicio tanto de la región de saturación magnética como de la contribución ordinaria de Hall y, así, el final de la contribución extraordinaria de Hall. Este campo está dado como la intersección entre la recta tangente a la curva de efecto Hall en la región de campo pequeño y aquella de campo alto, como se ilustra en la figura 10 b (de la misma forma se determinó H _S a partir de las curvas de los ciclos de histéresis de magnetización transversal).

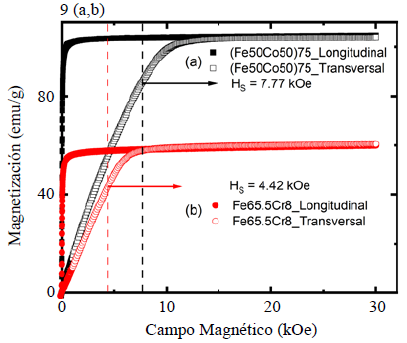
Figura 9 Ciclos de histéresis axial y transversal en función del campo magnético obtenidos a temperatura ambiente para a) FeCo y b) FeCr 

Es interesante observar que en las diferentes aleaciones de estudio, el H _S obtenido del ciclo de histéresis de la magnetización transversal coincidió bastante bien (dentro del error experimental) con el H _S obtenido de las curvas del efecto Hall. Este comportamiento era el esperado debido a que en ambos experimentos el campo magnético se aplicó en la dirección normal de la longitud de las cintas (muestras), e evidenció la gran coherencia entre estos experimentos. Las características de las curvas de efecto Hall descritas estuvieron, generalmente, en buen acuerdo con la siguiente expresión empírica para la resistividad de Hall (^{Blundell, 2001}),

donde H es el campo magnético, M es la magnetización, y R_o y R_e son los coeficientes Hall ordinario y extraordinario, respectivamente. Otra característica observada en la figura 10 a, b, c es que el cambio en la pendiente de las curvas de Hall fue más evidente en la muestra de MnFe que en las de FeCr y FeCo. El rango de campo en el que ese cambio ocurrió fue más pequeño en MnFe que en las otras dos muestras, lo que indica que el valor de H _S hasta donde se extiende la contribución extraordinaria de Hall fue menor en MnFe que en las otras dos muestras. Los valores de R_o y R_e obtenidos de las pendientes de las curvas de la figura 10 a, b, c en las regiones de campo alto (H > H_S) y pequeño (H < H_S) se presentan en la tabla 3. Estos evidenciaron la misma tendencia: en cada muestra, el valor de R_e fue mayor que el de R_o, lo que se esperaba debido a que en la región de campo pequeño el incremento en la pendiente de la curva se debe al incremento de H y de M, y, así, ambas contribuciones, la extraordinaria y la ordinaria, al efecto Hall están presentes. El incremento en la pendiente de la curva se debe tanto a R_o como a R_e. En la región de campo alto el sistema comenzó a saturar y, por ende, la magnetización M no aumentó más y la pendiente de la curva del efecto Hall se debió solo a la contribución de R_o. Otro hecho que se observa en la tabla 3 es que R_e(FeCo) > R_e(FeCr) > R_e(MnFe). Los valores de R_o presentan la misma tendencia que los de R_e. El signo positivo del efecto Hall indica que los electrones de conducción se comportaron ante el campo eléctrico y magnético como partículas de carga + e y masa efectiva m*, que ocupan orbitales cerca del máximo de la banda. Eso implica que su comportamiento magneto-eléctrico se desvió de la predicción del modelo de Drude, es decir, que el efecto Hall debería siempre ser negativo para metales simples. Los valores de R_e y R_o fueron del mismo orden de magnitud de los observados experimentalmente para aleaciones basadas en Fe (^{Prudnikova et al, 1997}). En concordancia con los valores de R y R , la densidad de los portadores n _c,cb y n _c,cα en campo pequeño y alto, presentaron el siguiente orden (Tabla 3): n _c,cb y n _c,ca de (MnFe) > n _c,cb y n _c,cα de (FeCr) > n _c,cb y n _c,cα de (FeCo). Los valores obtenidos para (H _s R_e, R_o) sugieren que la interacción espín-órbita fue más fuerte en FeCo que en FeCr y MnFe, lo cual es compatible con los resultados de anisotropía de esas muestras discutidos anteriormente (Figura 9 a, b). En contraste, la interacción RKKY fue más fuerte en MnFe que en las otras dos muestras, como lo sugiere la mayor densidad de los portadores de carga.

Figura 10 Resistividad Hall Vs. H a temperatura ambiente para a) FeCo, b) FeCr, y c) MnFe 

Tabla 3 Valores para H_s, coeficientes Hall (R_o, R_e), y densidad de portadores de carga a temperatura ambiente para las aleaciones bajo estudio 

A la luz de estos resultados, puede considerarse que en FeCo las interacciones de intercambio y de espín-orbita fueron suficientemente fuertes como para ubicarlo en la clase de universalidad del modelo 3d-XY con predominio de interacciones de corto alcance. En contraste, en FeCr y MnFe, las interacciones de intercambio y de espín-orbita no fueron suficientemente fuertes, por lo que es razonable considerar que la interacción RKKY estaba activa y predominó en ellas. Como conclusión, puede decirse que la interacción RKKY, que es de mediano a largo alcance, puede contribuir significativamente a causar el comportamiento de campo medio de esas aleaciones.

Conclusiones y otros comentarios

En este estudio se analizaron los exponentes críticos (β, δ, γ), los efectos de anisotropía magnética y Hall, la respuesta magneto-calórica con el exponente n que la caracteriza, y las interacciones magnéticas en muestras de las aleaciones FeCo, FeCr, y MnFe. Los valores determinados para (β, δ, γ) indicaron que FeCo pertenece a la clase de universalidad 3d-XY, mientras que FeCr y MnFe pertenecen a la clase de universalidad de campo medio. Las curvas de magnetización y termo-gravimétricas en presencia de un pequeño campo magnético indicaron un ordenamiento ferromagnético de largo alcance en FeCo y FeCr, y uno ferromagnètico incipiente o débil en MnFe. Dicho ordenamiento magnético se acompañó, de alguna manera, por los resultados del efecto Hall, que indicaban en FeCo y FeCr un comportamiento metálico menos fuerte que en MnFe. Además, FeCo y FeCr cumplieron de mejor manera que MnFe los requerimientos de una respuesta magneto-calórica, y pueden considerarse como candidatos potenciales idóneos para emplearse en la tecnología de refrigeración magnética a temperaturas moderadamente altas. El presente estudio plantea una ruta, indirecta pero basada en técnicas experimentales sencillas y bien establecidas (medidas de magnetización, anisotropía magnética y efecto Hall), para determinar algunas interacciones magnéticas que podrían estar activas en vidrios metálicos y aleaciones Heusler producidas por el método de melt-spinning, y para analizar la influencia de tales interacciones sobre los valores de (β, δ, γ), los cuales están relacionados con la respuesta magneto-calórica de esas aleaciones a través de los exponentes n y N. Esta ruta podría proporcionar un estímulo para que las comunidades de investigadores en materia condensada y magnetismo, especialmente en nuestro país, amplíen el estudio de la física básica de nuevas aleaciones ferromagnéticas blandas para su mejor comprensión y su aplicación en diferentes campos tecnológicos.