http://dx.doi.org/10.15446/dyna.v81n184.39699

Nonlinear time series forecasting using MARS

Predicción de series de tiempo no lineales usando MARS

Juan David Velásquez-Henao ^a, Carlos Jaime Franco-Cardona ^b & Paula Andrea Camacho ^c

^a Facultad de Minas, Universidad Nacional de Colombia, Colombia. jdvelasq@unal.edu.co
^b Facultad de Minas, Universidad Nacional de Colombia, Colombia. cjfranco@unal.edu.co
^c Facultad de Minas, Universidad Nacional de Colombia, Colombia. pcamach@unal.edu.co

Received: September 17^th, 2012. Received in revised form: December 1^th, 2013. Accepted: March 3^th, 2014.

Abstract
One of the most important uses of artificial neural networks is to forecast non-linear time series, although model-building issues, such as input selection, model complexity and parameters estimation, remain without a satisfactory solution. More of research efforts are devoted to solve these issues. However, other models emerged from statistics would be more appropriated than neural networks for forecasting, in the sense that the process of model specification is based entirely on statistical criteria. Multivariate adaptive regression splines (MARS) is a statistical model commonly used for solving nonlinear regression problems, and it is possible to use it for forecasting time series. Nonetheless, there is a lack of studies comparing the results obtained using MARS and neural network models, with the aim of determinate which model is better. In this paper, we forecast four nonlinear time series using MARS and we compare the obtained results against the reported results in the technical literature when artificial neural networks and the ARIMA approach are used. The main finding in this research, it is that for all considered cases, the forecasts obtained with MARS are lower in accuracy in relation to the other approaches.

Keywords: Artificial neural networks; comparative studies; ARIMA models; nonparametric methods.

Resumen
Uno de los usos más importantes de las redes neuronales artificiales es el pronóstico de series de tiempo no lineales, aunque los problemas en la construcción del modelo, tales como la selección de las entradas, la complejidad del modelo y la estimación de los parámetros, permanecen sin una solución satisfactoria. La mayoría de los esfuerzos en investigación están orientados a resolver estos problemas. Sin embargo, los modelos emergidos de la estadística podrían ser más adecuados que las redes neuronales para el pronóstico, en el sentido de que el proceso de especificación es basado enteramente en criterios estadísticos. La regresión adaptativa multivariada por tramos (MARS, por su sigla en inglés) es un método estadístico comúnmente usado para resolver problemas no lineales de regresión, y es posible usarlo para el pronóstico de series de tiempo. No obstante, faltan estudios que comparen los resultados obtenidos usando MARS y redes neuronales artificiales, con el fin de determinar cuál modelo es mejor. En este artículo, se pronostican cuatro series de tiempo no lineales usando MARS y se comparan los resultados obtenidos contra los resultados reportados en la literatura técnica cuando se usan las redes neuronales artificiales y la aproximación ARIMA. El principal hallazgo en esta investigación es que, para todos los casos considerados, los pronósticos obtenidos con MARS son inferiores en precisión respecto a otras aproximaciones.

Palabras clave: Redes neuronales artificiales; estudios comparativos; modelos ARIMA; métodos no paramétricos.

1 Introducción

La predicción de series de tiempo no lineales es una de las principales aplicaciones de las redes neuronales artificiales [1], siendo este un problema de interés particular para muchos científicos y profesionales provenientes de diversas áreas del conocimiento [2]. Una revisión profunda sobre la predicción de series de tiempo usando redes neuronales es presentada en [3]; ejemplos de casos específicos son presentados en [4-8].

Uno de los tipos más comunes de red neuronal que han sido utilizados para la predicción de series de tiempo son los perceptores multicapa (MLP, por su sigla en inglés) [3]; ello es debido a que pueden aproximar cualquier función continua definida en un dominio compacto con una precisión arbitraria [9-11]. No obstante, su proceso de especificación se basa en un conjunto de pasos críticos donde se emplean criterios empíricos y juicio experto [12-14]. Estos pasos están relacionados con el procesamiento de la información, la selección de las entradas a la red neuronal, de la cantidad correcta de neuronas a la capa oculta y la estimación de sus parámetros, entre otros. Las decisiones tomadas en cualquiera de los pasos del método de especificación, afectan el desempeño final del modelo en términos de su ajuste a los datos históricos y su capacidad de generalización; esto implica, que el proceso de especificación no es fácilmente reproducible, haciéndolo muy cuestionable [4]. Desde el trabajo seminal de Anders y Korn [15], se ha venido trabajando en metodologías de especificación basadas criterios estadísticos, pero no se ha llegado a definir criterios que sean aceptados en forma amplia por la comunidad científica. Aunque otras arquitecturas de redes neuronales, como las máquinas de vectores de soporte (SVM, por su sigla en inglés) [16,17] o las redes neuronales de arquitectura adaptativa (DAN2, por su sigla en inglés) [5], han sido usadas con éxito para la predicción de series de tiempo [8,18], persisten muchos de los problemas enunciados en la especificación del modelo.

La persistencia de los problemas planteados da pie a investigar sí otros métodos alternativos a las redes neuronales artificiales podrían ser usados de forma directa, pero, sin la existencia de dichos problemas en especificación del modelo. Una de dichas metodologías alternativas es MARS (multivariate adaptive regression splines) [19-21]; este es un modelo estadístico de regresión no lineal que se basa en la construcción de regiones que dividen el dominio de las variables de entrada, y en la asignación de un modelo de regresión lineal para cada una de las regiones obtenidas. El algoritmo de especificación de MARS está específicamente diseñado para seleccionar las variables de entrada y determinar la configuración óptima del modelo a partir de criterios estadísticos [19]; igualmente, es notoria la rapidez para la estimación de sus parámetros óptimos. MARS, al ser una metodología para construir modelos de regresión no lineal, podría realizar las mismas tareas que son usualmente abordadas con modelos de redes neuronales artificiales [22-25].

Debido a las ventajas teóricas y conceptuales presentadas por MARS, resulta natural su aplicación a la predicción de series de tiempo no lineales. Por ejemplo, Lewis y Stevens [26] muestran la relación entre MARS y los modelos TAR postulados por Tong [27], y usan MARS para analizar la serie de manchas solares de Wolf; en [6] se usa MARS para pronosticar serie de Mackey-Glass, y compara los resultados obtenidos con otros modelos; en [28] se pronostican tasas de cambio, mientras que en [29] se pronostican series hidrológicas; en [30] se analiza el comportamiento de los índices de producción industrial de Estados Unidos y Canadá.

Sin embargo, hay pocas evidencias que permitan determinar si MARS es realmente superior en precisión respecto a las redes neuronales para el pronóstico de series de tiempo. Por ejemplo, en [31] se concluye que MARS es más preciso que los perceptrones multicapa, la regresión lineal múltiple y las máquinas de vectores de soporte cuando se pronostica el índice de mercado Shangai B-share. No obstante, también se ha reportado que MARS es inferior en capacidad a ciertos tipos de modelos de redes neuronales artificiales; en [32] se concluye que las máquinas de vectores de soporte son más precisas que MARS cuando se pronostica la demanda urbana de agua; en [33] se presentan evidencias indicando que las redes neuronales artificiales son más precisas que MARS al pronosticar la demanda de electricidad; finalmente, en [34] se concluye que las redes neuronales recurrentes superan a MARS en el pronóstico de series de tiempo hidrológicas.

El objetivo de esta investigación es comparar la precisión de los pronósticos obtenidos con MARS y los obtenidos con diferentes arquitecturas de redes neuronales artificiales y con el modelo ARIMA, al pronosticar cinco series de tiempo no lineales. El trabajo práctico en esta investigación se centra en pronosticar dichas series usando MARS; para las redes neuronales y el modelo ARIMA se recurrió a resultados previamente reportados en otras investigaciones [4,5,7,8], de tal forma, que el lector debe remitirse a dichas fuentes para consultar detalles sobre los modelos alternativos considerados.

El resto de este artículo está organizado como sigue: En la próxima sección, se presenta el modelo MARS. Posteriormente, se describen los casos y de aplicación y se analizan los resultados obtenidos. Finalmente, se concluye.

2 Multivariate Adaptive Regression Splines

MARS es un modelo no paramétrico de regresión no lineal que permite explicar la dependencia de la variable respuesta respecto una o más variables explicativas [19]. MARS suele ser preferido sobre otros modelos no paramétricos de regresión debido a que: permite aproximar relaciones no lineales complejas a partir de los datos, sin postular una hipótesis sobre el tipo de no linealidad presente en los datos, tal como si ocurre en los modelos paramétricos de regresión; el algoritmo de construcción del modelo incorpora mecanismos que permite seleccionar las variables explicativas relevantes, descartando aquellas que no aportan información sobre la dinámica de la variable dependiente; el modelo resultante puede ser interpretado, al contrario de otros modelos de caja negra, como por ejemplo, las redes neuronales artificiales; y finalmente, la estimación de sus parámetros es computacionalmente eficiente y rápida, en oposición a como ocurren en los modelos de redes neuronales artificiales.

En la regresión basada en particionamiento recursivo, una función desconocida es aproximada dividiendo el espacio del dominio de las variables de entrada en regiones disyuntas, tal que:

donde es una función base que toma la forma de la función indicadora:

que toma el valor de uno si es su argumento es verdadero y cero en caso contrario. El algoritmo se inicia con , lo que es equivalente a decir que:

Luego se consideran dos regiones (). El punto crucial en el algoritmo es que la frontera de división es especificada como , donde es la -ésima componente del vector , y es un valor constante. Si es la función de paso unitario, que toma el valor de la unidad cuando , y cero en caso contrario, entonces, la nueva aproximación obtenida para dos regiones es:

donde las regiones y los coeficientes y son obtenidos tal que se maximice el ajuste a los datos. Nótese que para partir la región es necesario introducir una pareja de funciones .

Luego se toma . En este caso, se consideran todos los posibles modelos que se obtienen al partir una de las dos regiones obtenidas para , lo que permite llegar así a tres regiones. El algoritmo continúa adicionando regiones hasta que se cumpla algún criterio de parada. Así, en el modelo final y como resultado del algoritmo de particionamiento recursivo, las funciones base toman la forma de:

donde: es la cantidad de fronteras o particiones requeridas para definir la región ; toma los valores de indicando el sentido de la función de paso; indica la variable que introduce la frontera; y es el valor de la frontera. El modelo obtenido mediante particionamiento recursivo sufre de dos limitantes: en primer lugar, la función obtenida no es continua en las fronteras entre regiones; y segundo, la inhabilidad del modelo para aproximar funciones lineales o aditivas.

MARS es obtenido a partir de la metodología anterior introduciendo las siguientes modificaciones. En primer lugar, Friedman [19] reemplaza la función de paso por una curva spline de orden truncada por un lado:

donde es la ubicación de la frontera, y el símbolo + indica que se tome la parte positiva del argumento. De esta forma, las funciones base en el modelo final pueden escribirse como:

Usualmente , por lo que las funciones base son lineales por tramos. De esta forma, es común reescribir la ecuación anterior como:

O equivalentemente

La introducción de curvas spline causa que las regiones se traslapen en vez de ser disyuntas, generando la continuidad en las fronteras entre regiones. El siguiente cambio introducido en [19] es que cuando se realiza una partición que genera dos nuevas regiones hijas, la región padre original no es removida del modelo. Ello permite que tanto la región padre como sus dos regiones hijas puedan ser elegibles para ser divididas en pasos posteriores. Igualmente, se prohíbe que la misma variable sea usada más de una vez dentro del producto de términos que definen una función base ; ello para evitar que se generen polinomios de orden mayor a .

El algoritmo de especificación descrito hasta este punto corresponde a una fase de pasada hacia adelante, en la cual se crean las regiones en el espacio de variables de entrada. En una segunda fase, se evalúa si pueden eliminarse funciones base sin que se comprometa la calidad del modelo obtenido.

Si , entonces es demostrable que el modelo matemático generado por MARS es:

Agrupando todas las funciones base que envuelven los mismos conjuntos de variables explicativas, se llega a que la función puede reescribirse como:

donde a₀ corresponde a una constante, mas la suma de las funciones bases de una variable, mas la suma de todas las funciones base de dos variables, y así sucesivamente.

La selección final del modelo es realizada explorando modelos que difieren en la cantidad de regiones utilizadas_, y seleccionando aquel que minimice el criterio de validación cruzada generalizada, que es una medida que incorpora el ajuste a los datos y una penalización por la complejidad del modelo. En MARS, este criterio de selección es la falta de ajuste (LOF, por su sigla en inglés):

donde es el número final de funciones base, es la cantidad de datos, es el valor de la función que se desea aproximar, es el modelo con funciones base, es el vector de valores de las variables independientes en el punto , y es un factor de penalización por el aumento de la varianza debido al aumento de la complejidad del modelo:

es la matriz de datos de las funciones base. es un parámetro que representa el costo de la optimización de cada función base; cuando incrementa podría causar que se generen menos puntos de corte (fronteras). Friedman [19] sugiere ; por defecto, .

En esta sección se compara la precisión de los pronósticos obtenidos usando MARS versus los pronósticos obtenidos en otras investigaciones usando perceptrones multicapa, modelos ARIMA, DAN2 y máquinas de vectores de soporte. Se invita al lector a consultar los detalles de los pronósticos realizados con los modelos alternativos en las referencias citadas en esta sección. Para realizar los cálculos presentados se usó la función mars del paquete mda, implementado en el lenguaje R para el cómputo estadístico.

Para todos los casos considerados, se utilizaron como estadísticos de ajuste el error cuadrático medio (MSE, por su sigla en inglés) y el error medio absoluto (MAD, por su sigla en inglés).

La información disponible para cada serie de tiempo fue separada en un conjunto de datos para el entrenamiento o calibración de los parámetros del modelo, y en un conjunto para pronóstico o validación. Las cantidades de datos usados para el ajuste del modelo y para la predicción, son las mismas usadas en estudios previos para cada serie analizada.

Ya que el algoritmo de especificación de MARS permite la selección de las entradas relevantes al modelo, se procedió a realizar la especificación para cada serie estudiada, considerando como posibles regresores los rezagos 1-, donde es el máximo rezago utilizado en estudios previos. Igualmente, se varió el parámetro (penalización por la cantidad de funciones base) desde 2 hasta 4.

3.1 Serie PAPER
Corresponde a las ventas mensuales de papel impreso y escrito en miles de francos franceses entre 1/1963 y 12/1972. En [35] se reporta que el modelo ARIMA con menor error cuadrático medio (MSE) para representar la dinámica de la serie es de orden (0, 1, 1) X (0, 1, 1)₁₂ usando la totalidad de la información. No obstante, para la evaluación del pronóstico usando modelos no lineales, se usan las primeras 100 observaciones para el ajuste de los modelos, y las 20 restantes para la predicción por fuera de la muestra de calibración. La serie es pronosticada sin ninguna transformación. Esta serie es graficada en la Fig. 1.

En la literatura técnica se ha reportado que los mejores pronósticos (por modelo) se obtienen con un modelo ARIMA que usa los rezagos 1, 12, y 13 [5], y con los rezagos 1, 7 y 12 para las redes neuronales tipo MLP [5], DAN2 [5] y SVM [8]. Los estadísticos de ajuste para estos modelos son reportados en la Tabla 1.

Al igual que para los casos reportados en la literatura, MARS fue estimado sobre los primeros 100 datos, y luego se procedió a realizar el pronóstico del siguiente mes usando los datos reales, para las 20 observaciones restantes. Para la especificación de MARS se consideraron los rezagos desde 1 hasta el 13. El modelo final obtenido es únicamente función de .

En la Tabla 1 se presentan los estadísticos de ajuste obtenidos. Para las muestras de entrenamiento y calibración, MARS es inferior al modelo ARIMA en términos de la precisión obtenida. No obstante, la precisión de DAN2 es notoria y sigue siendo el modelo que mejor se adapta a la dinámica de la serie analizada. Puede decirse que MARS es superior a las SVM, ya que su error de ajuste a la muestra de calibración es mejor (el 86% del MSE reportado para la muestra de entrenamiento), y tiene un error prácticamente igual para la muestra de pronóstico.

En investigaciones previas se encontró que: el mejor modelo ARIMA para pronosticar la serie es de orden (2,1,0)(1,0,0)₁₂ [5], lo que equivale a usar los rezagos 1-3 y 12-15; el mejor MLP usa los rezagos 1-12 [5]; igualmente en [5] se reportaron los resultados para modelos DAN2 que usan los siguientes grupos de rezagos: 1-3, 12-15; 1-12; y finalmente, 1-15. En [8] se pronostica esta misma serie con dos SVM que usa los grupos de rezagos 1-3, 12-15, y 1-12. Los estadísticos de ajuste para estos modelos son reportados en la Tabla 2.

El algoritmo de selección de MARS fue aplicado sobre los rezagos 1-15; el modelo final obtenido pronostica el valor actual como función de los rezagos 1, 3 y 12. Los estadísticos de ajuste calculados para MARS se reportan en la Tabla 2. En términos del MSE para la muestra de entrenamiento, MARS es el séptimo modelo en calidad de ajuste en un ordenamiento del menor al mayor MSE; el MLP reportado en [5] presenta el mayor MSE entre todos los modelos. No obstante, es ligeramente superior en la precisión de la predicción, ocupando el quinto lugar. Los valores del MSE calculados para MARS, para las muestras de entrenamiento y pronóstico, son superiores en más de 3 veces respecto a los mejores valores del MSE. DAN2 sigue siendo el mejor modelo tanto en entrenamiento como en validación.

Esta serie es usada en [7] para evaluar el desempeño de un modelo ARIMA, un MLP y un modelo híbrido que combina las dos metodologías anteriores; en [7] se reporta que el MLP tiene una estructura de 7 entradas correspondientes a los primeros 7 rezagos de la serie, 5 neuronas en la capa oculta, y una neurona de salida. Ghiassi, Saidane y Zimbra [5] probaron diferentes configuraciones del modelo DAN2 que difieren en los rezagos utilizados para su especificación. Estos mismos grupos de rezagos fueron usados por Velásquez, Olaya y Franco [8] para evaluar la precisión de la predicción usando SVM. Los resultados obtenidos en estas investigaciones son reportados en la Tabla 3.

Al igual que en los otros casos analizados, se aplicó el algoritmo de especificación de MARS considerando que las variables explicativas corresponden a los valores rezagados de la serie de tiempo entre uno y diez años. Este último valor, es el máximo rezago usado en [5]. Para este caso, el algoritmo de especificación reportó los rezagos 1, 2, 3, 5, 9 como relevantes.

Para esta serie de tiempo, MARS se destaca por su baja precisión en el entrenamiento y la predicción. En términos del MSE, es el penúltimo modelo considerando la muestra de entrenamiento, mientras que presenta la precisión más baja entre todos los modelos para la muestra de predicción. Los MSE de MARS son más de siete veces los mejores MSE reportados en la Tabla 3.

Esta serie es analizada en [35], y se sugiere que un modelo ARIMA de orden (3, 1, 0) sería el más adecuado para representar su dinámica. Ghiassi, Saidane y Zimbra [5] reportan los resultados obtenidos al estimar: un MLP con rezagos 1, 2, 3 y 4, y DAN2 con los grupos de rezagos del 1-3 y de 1-4. Velásquez, Olaya y Franco [8] realizan la predicción de esta serie usando un SVM que tiene como entradas los rezagos 1-4. Los estadísticos de ajuste para dichos modelos aparecen en la Tabla 4.

Los rezagos uno al cuatro fueron utilizados para especificar el modelo MARS. El modelo final seleccionado usa únicamente los rezagos 1 y 2. Al analizar la Tabla 4, resulta notoria la falta de precisión de MARS. Presente el MSE y el MAD más altos entre todos los modelos, para ambas muestras de datos (entrenamiento y predicción). En ambos casos, el MSE calculado para MARS es más de tres veces el menor MSE reportado en la Tabla 4.

4 DISCUSIÓN

En las secciones anteriores se ha discutido el principio matemático sobre el que está fundamentado MARS y sus posibles ventajas sobre otros modelos de caja negra como las redes neuronales artificiales, tales como su velocidad de estimación y su capacidad de seleccionar variables relevantes. No obstante, la experimentación realizada sobre cuatro series benchmark que ya han sido utilizadas en otras investigaciones para la comparación de modelos no lineales de pronóstico, revela que MARS tiene dificultades para capturar la dinámica de las series consideradas. En esta Sección se indaga sobre el por qué se da esta situación.

El particionamiento recursivo es un principio para la aproximación de funciones bastante diferente al utilizado por los MLP. Por ejemplo, el MLP de la Tabla 4 podría representarse matemáticamente como:

donde ; 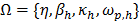, con y , son los parámetros del modelo; es la cantidad de neuronas en la capa oculta; y es la función de activación de las neuronas. En este caso, la entrada neta a la -ésima neurona de la capa oculta:

es un modelo autorregresivo de orden . Así, un MLP puede definirse como la combinación no lineal de tantos modelos autorregresivos como neuronas tenga la capa oculta. Nótese, que un modelo autorregresivo es la combinación lineal de todos los rezagos considerados en el modelo. La ecuación equivalente de MARS es claramente diferente; véase la ecuación de la Tabla 5 para la serie INTERNET.

Una explicación sobre el desempeño de MARS se basa en la forma a que se llega a dicha ecuación. Cuando no hay variables explicativas (rezagos en el caso de series de tiempo), MARS se reduce a una constante puesto que no hay regiones definidas:

Para que una variable explicativa sea incorporada al modelo, ella debe ser seleccionada durante el particionamiento recursivo, de manera que debe entrar en la forma del término:

el cual hace parte de una función base . Así, el algoritmo de especificación no permite que se considere la variable explicativa, sin que su dominio sea divido un término. Pareciera entonces, que MARS sufre de dificultades para aproximar modelos autorregresivos.

Por otra parte, una SVM representa la dinámica de una serie de tiempo como:

donde: es una constante, son los factores de ponderación de la función de núcleo , definida como:

En la ecuación anterior , mientras que representa un subconjunto de los regresores de la muestra de entrenamiento; véase [8]. En este caso, el modelo matemático que representa un SVM también difiere tanto de MARS como de los MLP. En este sentido, no puede considerarse como la transformación no lineal de un modelo autorregresivo, lo que explica, al menos en parte, su bajo desempeño en el pronóstico.

Uno de los principales problemas en el pronóstico de series de tiempo usando redes neuronales artificiales, es que su proceso de especificación está basado primordialmente en criterios heurísticos y juicio experto. Esto hace el proceso subjetivo quitando, en alguna medida, credibilidad a los resultados obtenidos. En este contexto, el uso de modelos alternativos a las redes neuronales artificiales que se basen en criterios objetivos y bien estructurados gana mucha importancia.

MARS es un modelo no paramétrico y no lineal de regresión cuya especificación está basada en criterios estadísticos bien establecidos que permiten seleccionar los regresores relevantes y la complejidad óptima del modelo, y cuyos parámetros óptimos pueden ser calculados rápidamente.

En este trabajo se explora la capacidad de MARS en el pronóstico de cuatro series de tiempo no lineales, que ya han sido utilizadas en la literatura para la comparación de modelos estadísticos y redes neuronales artificiales.

El desempeño de MARS para su ajuste a la muestra de calibración, así como de su precisión en el pronóstico, fue pobre en comparación con los demás modelos considerados (modelos ARIMA, perceptrones multicapa, máquinas de vectores de soporte y DAN2). Posiblemente, la razón de este comportamiento está relacionada con el algoritmo de especificación del modelo. Es así como MARS selecciona sólo un subconjunto de los retardos utilizados en otros estudios, y, consecuentemente, pierde poder explicativo. Adicionalmente, la estructura matemática del modelo final obtenido usando el algoritmo empleado por MARS difiere de la obtenida utilizando los modelos ARIMA y varios tipos de redes neuronales artificiales; consecuentemente, este aspecto también impacta el desempeño del modelo.

Como trabajo futuro, se plantea la posibilidad de adicionar una estructura autorregresiva lineal en la que se consideren todos los rezagos de la serie, más la sumatoria de las funciones base. Otra posibilidad consiste en considerar una estructura más compleja para los factores con que se construyen las funciones base, tal que se use una combinación de regresores, en vez de usar solamente una variable explicativa.

Referencias

[1] Kasabov. N. Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering. Massachusetts Institute of Technology. 1998.         [ Links ]

[2] Tong, H., Non-linear time series a dynamical system approach. Claredon Press Oxford. 1990.         [ Links ]

[3] Zhang, G., Patuwo, E.B. and Hu, M.Y., Forecasting with artificial neural networks: the state of the art. International Journal of Forecasting, 14 (1), pp. 35-62, 1998.         [ Links ]

[4] Faraway, J. and Chatfield, C., Time series forecasting with neural networks: A comparative study using the Airline data. Applied Statistics, 47 (2), pp. 231-250, 1998.         [ Links ]

[5] Ghiassi, M., Saidane, H. and Zimbra, D.K., A dynamic artificial neural network model for forecasting time series events. International Journal of Forecasting, 21 (2), pp. 341-362, 2005.         [ Links ]

[6] Velásquez, J.D., Pronóstico de la Serie de Mackey-Glass usando modelos de Regresión no Lineal. Dyna: 71 (142), pp. 85-95, 2004.         [ Links ]

[7] Zhang, G., Time Series forecasting using a hybrid ARIMA and neural network model. Neurocomputing: 50, pp. 159-175, 2003.         [ Links ]

[8] Velásquez, J.D., Olaya, Y. y Franco, C.J., Predicción de series temporales usando máquinas de vectores de soporte. Ingeniare, 18 (1), pp. 64-75, 2010.         [ Links ]

[9] Cybenko, G., Approximation by superpositions of a sigmoidal function. Mathematics of Control: Signals and Systems, 2, pp. 202-314, 1989.         [ Links ]

[10] Hornik, K., Stinchcombe, M. and White, H., Multilayer feedforward networks are universal approximators. Neural Networks, 2, pp. 359-366, 1989.         [ Links ]

[11] Funahashi, K., On the approximate realization of continuous mappings by neural networks. Neural Networks: 2, pp. 183-192, 1989.         [ Links ]

[12] Masters, T., Practical Neural Network Recipes in C ++. Academic Press, New York, 1993.         [ Links ]

[13] Masters, T., Neural, Novel and Hybrid Algorithms for Time Series Prediction. John Wiley and Sons, Inc. First Edn. 1995.         [ Links ]

[14] Kaastra, I. and Boyd, M., Designing a neural network for forecasting financial and economic series. Neurocomputing, 10, pp. 215-236, 1996.         [ Links ]

[15] Anders, U. and Korn, O., Model selection in neural networks. Neural Networks, 12, pp. 309-323, 1999.         [ Links ]

[16] Vapnik, V.N., The Nature of Statistical Learning Theory. Springer, N.Y. 1995.         [ Links ]

[17] Vapnik, V.N., Golowich, S.E. and Smola, A.J., Support vector method for function approximation, regression estimation, and signal processing. Advances in Neural Information Processing Systems, 9, pp. 281-287, 1996.         [ Links ]

[18] Velásquez, J.D., Franco, C.J. y Olaya, Y., Predicción de los precios promedios mensuales de contratos despachados en el mercado mayorista de electricidad en Colombia usando máquinas de vectores de soporte. Cuadernos de Administración, 23 (40), pp. 321-337, 2010.         [ Links ]

[19] Friedman, J.H., Multivariate adaptive regression splines (with discussion). Annals of Statistics, 19, pp. 1-141, 1991.         [ Links ]

[20] Friedman, J.H. Fast MARS. Dept. of Statistics, Stanford University Technical Report. 1993.         [ Links ]

[21] Friedman, J.H. and Roosen, C.B., An introduction to multivariate adaptive regression splines. Statistical Methods in Medical Research, 4(3), pp. 197-217, 1995.         [ Links ]

[22] Chou, S.M., Lee, T.S. and Shao, Y.E., Mining the breast cancer pattern using artificial neural networks and multivariate adaptive regression splines. Expert Systems with Applications, 27 (1), pp. 133-142, 2004.         [ Links ]

[23] De Veaux, R.D., Psichogios, D.C. and Ungar, L.H., A comparison of two nonparametric estimation schemes: MARS and neural networks. Computers & Chemical Engineering, 17 (8), pp. 819-837, 1993.         [ Links ]

[24] Tian-Shyug, L., Chih-Chou, C., Yu-Chao, C. and Chi-Jie, L., Mining the customer credit using classification and regression tree and multivariate adaptive regression splines. Computational Statistics & Data Analysis, 50 (4), pp. 1113-1130, 2006.         [ Links ]

[25] Deichmann, J., Eshghi, A., Haughton, D., Sayek, S. and Teebagy, N., Application of multiple adaptive regression splines (MARS) in direct response modeling. Journal of Interactive Marketing, 16 (4), pp. 15-27, 2002.         [ Links ]

[26] Lewis, P.A.W. and Stevens, J.G., Nonlinear Modeling of Time Series Using Multivariate Adaptive Regression Splines (MARS). Journal of the American Statistical Association, 86 (416), pp. 864-877, 1991.         [ Links ]

[27] Tong, H., Threshold models in non-linear time series analysis. Heidelberg: Sprenger-Verlag. 1983.         [ Links ]

[28] De Gooijer, J.G., Ray, B.K. and Kräger, H., Forecasting exchange rates using TSMARS. Journal of International Money and Finance, 17 (3), pp. 513-534, 1998.         [ Links ]

[29] Coulibaly, P. and Baldwin, C.K., Nonstationary hydrological time series forecasting using nonlinear dynamic methods. Journal of Hydrology, 307 (1-4), pp. 164-174, 2005.         [ Links ]

[30] Heather, M.A. and Ramsey, J.B. U.S. and Canadian industrial production indices as coupled oscillators. Journal of Economic Dynamics and Control, 26 (1), pp. 33-67,2002.         [ Links ]        [ Links ]

[32] Herrera, M., Torgo, L., Izquierdo, J., Pérez-García, R., Predictive models for forecasting hourly urban water demand. Journal of Hydrology, 387 (1-2), pp. 141-150, 2010.         [ Links ]

[33] Fidalgo, J.N., Matos, M.A., Forecasting Portugal global load with artificial neural networks. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 4669 LNCS (PART 2), pp. 728-737, 2007.         [ Links ]

[34] Coulibaly, P., Baldwin, C.K., Nonstationary hydrological time series forecasting using nonlinear dynamic methods. Journal of Hydrology, 307 (1-4), pp. 164-174 2005.         [ Links ]

[35] Makridakis, S.G., Wheelwright, S.C. and Hyndman, R.J., Forecasting: Methods and applications. 3rd edition. New York. John Wiley & Sons, 1998.         [ Links ]

J. D. Velásquez-Henao, received the Bs. Eng in Civil Engineering in 1994, the MS degree in Systems Engineering in 1997, and the PhD degree in Energy Systems in 2009, all of them from the Universidad Nacional de Colombia. Medellin, Colombia. From 1994 to 1999, he worked for electricity utilities and consulting companies within the power sector and since 2000 for the Universidad Nacional de Colombia. Currently, he is a Full Professor in the Computing and Decision Sciences Department, Facultad de Minas, Universidad Nacional de Colombia. His research interests include: simulation, modeling and forecasting in energy markets; nonlinear time-series analysis and forecasting using statistical and computational intelligence techniques; and optimization using metaheuristics. http://orcid.org/0000-0003-3043-3037

Carlos J. Franco is a Full Professor in the Department of Computer and Decision Sciences at the National University of Colombia in the Medellin campus. Carlos is professor in subjects such as complex systems, system modeling and energy markets. His research area is on energy systems analysis, including policies evaluation and strategies formulation. His recent work includes low carbon economies, demand response, electric markets integration and bio-fuels, among others. He has a degree in Civil Engineering, a Master Degree in Water Resources Management, and a PhD in Engineering, all from the National University of Colombia.