Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.186 Medellín July/Aug. 2014
https://doi.org/10.15446/dyna.v81n186.40023
http://dx.doi.org/10.15446/dyna.v81n186.40023
Viscosity and viscometric properties of Glycine in aqueous solutions of Sodium Thiosulfate Pentahydrate (Na2S2O3 .5H2O) at different temperatures
Viscosidades y propiedades viscosimetricas de la Glicina en soluciones acuosas de Tiosulfato de Sodio Pentahidratado (Na2S2O3 .5H2O) a diferentes temperaturas
Manuel Silvestre Páez-Meza a, Gustavo Manuel Alvarino-Bettín b & Plinio de los Santos Cantero-López c
a Grupo de Fisicoquímica de Mezclas Líquidas, Universidad de Córdoba, Colombia. mspaezm@unal.edu.co, mspaezm@gmail.com
b Grupo Física Teórica y Aplicada, Universidad de Córdoba, Colombia. alvarinog@hotmail.com
c Grupo de Fisicoquímica de Mezclas Líquidas, Universidad de Córdoba, Colombia. pliniocantero@gmail.com
Received: September 23th, 2013. Received in revised form: April 21th, 2014. Accepted: Julio 25th, 2014.
Abstract
Flowing times of Glycine in aqueous solutions Sodium Thiosulfate Pentahydrate (0.01-2.0 mol kg-1) using an AMVn Anton Paar viscometer at temperatures of (283.15; 288.15; 293.15; 298.15; 303.15; 308.15, 313.15 and 318.15) K and 101.1 Kpa.From the data obtained, the absolute viscosity, viscosity B-coefficients, slope ( 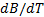 ),the
),the  ,adjustable parameters of the equation of Out and Los (
,adjustable parameters of the equation of Out and Los ( 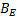 ,
, 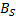 ,
,  ), activation parameters of viscous flow (
), activation parameters of viscous flow ( 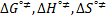 ) were calculated , the values obtained for these parameters were discussed in terms of the interactions present in solution.
) were calculated , the values obtained for these parameters were discussed in terms of the interactions present in solution.
Keywords: Viscosity, Activation parameters;Viscous flow; Excess properties; Interactions.
Resumen
Se determinaron los tiempos de flujo de la Glicina en soluciones acuosas de Tiosulfato de Sodio Pentahidratado (0.01-2.0 mol Kg-1) usando un viscosímetro Anton Paar modelo AMVn a las temperaturas de (283.15; 288.15; 293.15; 298.15; 303.15; 308.15,313.15 y 318.15) K y 101.1 Kpa. A partir de los datos obtenidos se calcularon las viscosidades absolutas, los coeficientes B de viscosidad, la pendiente ( 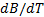 ),el
),el  ,los parámetros ajustables de la ecuación de Out y Los (
,los parámetros ajustables de la ecuación de Out y Los ( 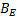 ,
, 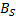 ,
,  ), los parámetros de activación del flujo viscoso (
), los parámetros de activación del flujo viscoso ( 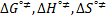 ), los valores obtenidos para estos parámetros fueron discutidos en términos de las interacciones presentes en solución.
), los valores obtenidos para estos parámetros fueron discutidos en términos de las interacciones presentes en solución.
Palabras clave: Viscosidad; Parámetros de activación; Flujo viscoso; Interacciones.
1. Introducción
La viscosidad es una propiedad de transporte que es importante tanto desde el punto vista teórico como práctico. Es por ello que estudios sistemáticos de las propiedades físicas de mezclas líquidas multicomponentes sean requeridos para permitir un mejor conocimiento de la teoría del estado líquido. En este sentido, la viscosidad de soluciones de electrolitos es de gran interés a nivel científico debido a que las variaciones de la viscosidad con la temperatura y la composición del disolvente permiten tener una mayor comprensión de las interacciones ión-solvente en los sistemas de electrolitos ,de igual forma a nivel ingenieril la viscosidad de electrolitos tiene un rol sumamente relevante debido a su importancia en numerosos sistemas industriales entre los cuales se destacan los procesos electroquímicos así como cálculos de ingeniería química relacionados con el flujo de fluidos, transferencia de calor y masa [1,2].
En este orden de ideas, el estudio de una propiedad termofísica como la viscosidad en sistemas de aminoácidos en solventes mixtos resulta interesante debido a que este tipo de sistemas constituye un modelo apropiado para el estudio de las interacciones en péptidos y proteína-solvente que son esenciales en el estudio de diversos procesos biológicos[3,4].En este sentido en macromoléculas como las proteínas propiedades como la estabilidad conformacional, solubilidad, actividad enzimática, disociación en subunidades, desnaturalización, separación y purificación son claramente influenciadas por diversas interacciones moleculares entre los grupos funcionales presentes que son direccionados por factores como la temperatura, presencia de sustancias de bajo peso molecular como sustratos, coenzimas, inhibidores y activadores que específicamente ligan a la estructura nativa y el medio en el cual se encuentran disueltas[5,6].
Es ampliamente conocido que uno de los medios que ejerce grandes efectos sobre las propiedades anteriormente mencionadas son las soluciones salinas [5,7]. Es así como se ha establecido claramente que iones de metales juegan un papel crucial en los procesos celulares los cuales involucran la participación de proteínas transmembrana como es el caso de la bomba de sodio y potasio en donde estos dos iones participan en el balance osmótico y el mantenimiento del volumen celular [8-10].Por tal motivo, en este trabajo se reportan las viscosidades de la (h) de la Glicina(Gli) en diferentes molalidades de Tiosulfato de Sodio Pentahidratado (Na2S2O3.5H2O) a una presión atmosférica de 101.1 Kpa a las temperaturas de (283.15; 288.15; 293.15; 298.15, 303.15; 308.15 313.15 y 318.15) K.Los valores experimentales de h se usaron para calcular los, coeficientes B de viscosidad, la pendiente (  ), el
), el  , los parámetros ajustables de la ecuación de Out y Los (
, los parámetros ajustables de la ecuación de Out y Los (  ,
, 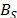 ,
, 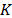 ), los parámetros de activación del flujo viscoso (
), los parámetros de activación del flujo viscoso ( 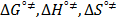 ) así como las contribuciones por mol del solvente
) así como las contribuciones por mol del solvente  y del soluto
y del soluto 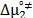 a la energía libre, los valores obtenidos para estos parámetros fueron discutidos en términos de las interacciones presentes en solución.
a la energía libre, los valores obtenidos para estos parámetros fueron discutidos en términos de las interacciones presentes en solución.
2. Parte Experimental
Los reactivos empleados son los siguientes: Glicina (99% de pureza, Alfa Aesar), Tiosulfato de Sodio Pentahidratado (99% de pureza, Merck) la Glicina fue doblemente recristalizada desde soluciones acuosas de etanol y secada al vacío sobre P2O5.El agua usada fue desgasificada, doblemente destilada y desionizada garantizando una conductividad menor de 2 mS cm-1.
Las soluciones fueron preparadas gravimétricamente mediante una balanza (OHAUS modelo Explorer) con una sensibilidad de ± 1 x 10-4 g, en botellas herméticamente cerradas para evitar perdida por evaporación de alguno de los componentes.
Las medidas de la viscosidad absoluta fueron hechas con un viscosímetro Anton Paar modelo AMVn. El principio de medición de este equipo se basa en la ley de Stoke. Así, la viscosidad de líquidos puros y su composición es determinada observando el tiempo requerido para que una esfera sólida (acero), recorra una distancia fija entre los dos sensores inductivos en un tubo cilíndrico inclinado que contiene la muestra .El viscosímetro arroja los tiempos de flujo y calcula automáticamente la viscosidad absoluta previa incorporación de la densidad de la muestra las cuales fueron obtenidas previamente utilizando un densímetro de tubo vibratorio Anton Paar modelo DMA 5000. Así es posible tomar medidas en un amplio intervalo de viscosidad con una exactitud de ± 0.01K, garantizada mediante un termostato tipo Peltier. La incertidumbre absoluta en los datos de viscosidad (  ) fue calculada usando el método de propagación de errores usando la ecuación (1):
) fue calculada usando el método de propagación de errores usando la ecuación (1):

Donde  es la incertidumbre en la constante de calibración K, t es el tiempo de flujo,
es la incertidumbre en la constante de calibración K, t es el tiempo de flujo,  (0.01 g/cm3) es la incertidumbre en la densidad de la bola (7.66 g/cm3),
(0.01 g/cm3) es la incertidumbre en la densidad de la bola (7.66 g/cm3),  es la densidad de la solución. La incertidumbre promedio en la viscosidad es del orden ± 0.001m Pa s.
es la densidad de la solución. La incertidumbre promedio en la viscosidad es del orden ± 0.001m Pa s.
3. Resultados y Discusión
Las viscosidades (h) obtenidas en este trabajo desde 283.15K hasta 318.15K para las diferentes concentraciones de Glicina y Tiosulfato de Sodio Pentahidratado se muestran en la Tabla 1. En la Tabla 1, se observa que los valores de viscosidad (h) aumentan con el aumento de la concentración de Glicina y con el aumento de la composición del solvente mixto y disminuyen con el aumento de la temperatura.
Las viscosidades relativas (  ) de la Glicina en agua y en las soluciones del solvente mixto fueron calculadas usando la ecuación (1)
) de la Glicina en agua y en las soluciones del solvente mixto fueron calculadas usando la ecuación (1)

Donde h es la viscosidad de la solución y  es la viscosidad del solvente mixto. Los datos de viscosidad relativa fueron analizados utilizando la ecuación de Jones-Doles (3)
es la viscosidad del solvente mixto. Los datos de viscosidad relativa fueron analizados utilizando la ecuación de Jones-Doles (3)

Donde A es el coeficiente de Falkenhagen que ofrece información sobre las interacciones soluto-soluto, B es un coeficiente empírico es una medida de las interacciones soluto-solvente y depende fundamentalmente del tamaño ,la forma y la carga del soluto[11,12].No obstante, la gran mayoría de los estudios viscosimétricos [13-16] en soluciones de electrolitos han centrado su interés en obtener solo información de las interacciones soluto-solvente en mezclas seudobinarias en vez de las interacciones soluto-soluto utilizando la expresión (3) en la forma:
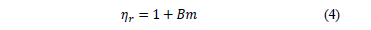
En este trabajo, los valores del coeficiente B fueron calculados a partir de la ecuación (4), debido a que la región de composición en estudio no es altamente diluida [12,16]; y son reportados en la Tabla 2.
La Tabla 2 muestra que los valores coeficiente B son positivos a lo largo de todas las composiciones e isotermas de estudio, lo que sugiere que en el sistema se favorecen las interacciones soluto-solvente, que podrían ser clasificadas de la siguiente forma [17,18]:
- Interacciones Ión - Ión entre el ión Na+ del solvente mixto y el grupo COO- de la Glicina .
- Interacciones Ión - Ión entre el ión
 y el grupo NH3+ de la Glicina.
y el grupo NH3+ de la Glicina.
La dependencia del coeficiente B con respecto a la temperatura fue expresada usando la ecuación de Out y Los [2]

Donde  ,
, 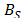 ,
, 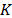 son parámetros ajustables,
son parámetros ajustables,  es la
es la
temperatura en Kelvin, 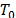 = 273.15 K. Los valores de
= 273.15 K. Los valores de  ,
, 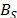 y
y 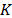 para cada una de las composiciones en estudio son presentados en la Tabla 4 junto con su respectiva desviación estándar poblacional (s).
para cada una de las composiciones en estudio son presentados en la Tabla 4 junto con su respectiva desviación estándar poblacional (s).
Adicionalmente se calcularon los valores de  y son reportados en la Tabla 3. En la Tabla 3 se observa que los valores de
y son reportados en la Tabla 3. En la Tabla 3 se observa que los valores de  son positivos a lo largo de todas las isotermas y composiciones de Na2S2O3.5H2O, comportamiento que indica que la Glicina actúa como un disruptor de la estructura del solvente. Los valores del los coeficientes B de transferencia (
son positivos a lo largo de todas las isotermas y composiciones de Na2S2O3.5H2O, comportamiento que indica que la Glicina actúa como un disruptor de la estructura del solvente. Los valores del los coeficientes B de transferencia (  ) desde el agua a soluciones acuosas de Na2S2O3.5H2O fueron obtenidos mediante la ecuación (6)
) desde el agua a soluciones acuosas de Na2S2O3.5H2O fueron obtenidos mediante la ecuación (6)

Los valores de  obtenidos son reportados en la Tabla 5.
obtenidos son reportados en la Tabla 5.
De la Tabla 5 se observa que los valores de  son positivos en todas las isotermas y composiciones de estudio; lo cual podría indicar que en el sistema las interacciones son altamente específicas [16].Los datos de viscosidad han sido analizados utilizando la teoría de Eyring [19], esta supone que las moléculas se mueven por cada una de las posiciones de equilibrio a través sus estados de transición en donde los enlaces intermoleculares se estiran al pasar de un estado de equilibrio a otro. En este sentido para un líquido puro se ha demostrado que se cumple la expresión (7).
son positivos en todas las isotermas y composiciones de estudio; lo cual podría indicar que en el sistema las interacciones son altamente específicas [16].Los datos de viscosidad han sido analizados utilizando la teoría de Eyring [19], esta supone que las moléculas se mueven por cada una de las posiciones de equilibrio a través sus estados de transición en donde los enlaces intermoleculares se estiran al pasar de un estado de equilibrio a otro. En este sentido para un líquido puro se ha demostrado que se cumple la expresión (7).
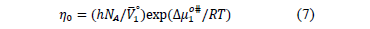
Donde 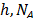 ,
, 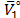 ,
,  y T es la constante de Planck, el número de Avogadro, el volumen molar parcial del solvente ,la energía libre de activación por mol del solvente, la constante universal de los gases y la temperatura en Kelvin respectivamente.
y T es la constante de Planck, el número de Avogadro, el volumen molar parcial del solvente ,la energía libre de activación por mol del solvente, la constante universal de los gases y la temperatura en Kelvin respectivamente.
Feakins y colaboradores [20] aplicaron la teoría del estado de transición al tratamiento de las viscosidades relativas de soluciones, mostrando que el coeficiente B puede escribirse como:
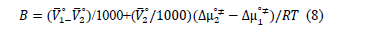
Donde 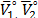 on el volumen molar parcial solvente y del soluto cuando
on el volumen molar parcial solvente y del soluto cuando 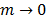 ,
,  es la contribución por mol del soluto. De esta forma
es la contribución por mol del soluto. De esta forma 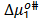 y
y 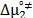 fueron calculado a partir de las expresiones (9) y (10) respectivamente
fueron calculado a partir de las expresiones (9) y (10) respectivamente

La energía total de activación del flujo viscoso fue calculada mediante la expresión (11)

Donde  ,
,  son las fracciones molares del solvente y del soluto respectivamente.Los valores obtenidos para
son las fracciones molares del solvente y del soluto respectivamente.Los valores obtenidos para  ,
, 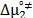 y
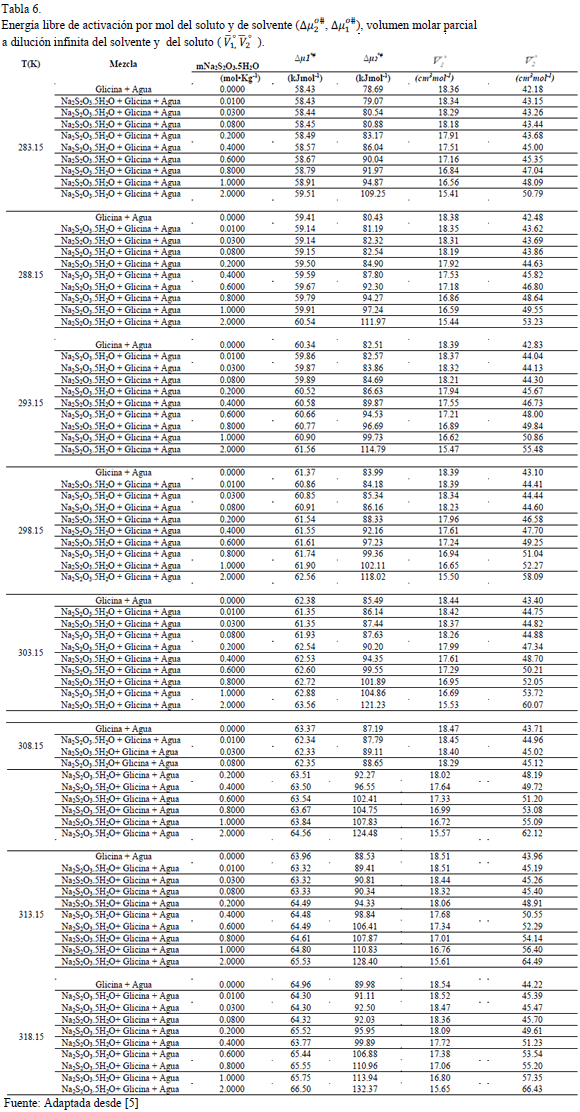
y  son presentados en las Tablas 6 y 7 respectivamente. En la Tabla 6 se observa que los valores de
son presentados en las Tablas 6 y 7 respectivamente. En la Tabla 6 se observa que los valores de 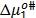 son aproximadamente constantes a todas las temperaturas y composiciones de solvente mixto en estudio, lo que indica que los valores de
son aproximadamente constantes a todas las temperaturas y composiciones de solvente mixto en estudio, lo que indica que los valores de  dependen principalmente del coeficiente B y de la cantidad
dependen principalmente del coeficiente B y de la cantidad 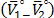 .
.
Los valores de  y
y 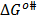 son positivos y mayores que los valores de
son positivos y mayores que los valores de  ; lo que sugiere que el estado de transición es menos favorecido en presencia de Glicina y que la formación de este estado va acompañado de la disrupción y distorsión de los enlaces intermoleculares en la estructura del disolvente [15,21].
; lo que sugiere que el estado de transición es menos favorecido en presencia de Glicina y que la formación de este estado va acompañado de la disrupción y distorsión de los enlaces intermoleculares en la estructura del disolvente [15,21].
Este hecho sugiere que las interacciones que involucran a los iones presentes en el solvente mixto (Na+ , 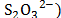 con los centros cargados de la Glicina (COO-, NH3+) son fuertes y por consiguiente ocurre un favorecimiento de las interacciones soluto-solvente.
con los centros cargados de la Glicina (COO-, NH3+) son fuertes y por consiguiente ocurre un favorecimiento de las interacciones soluto-solvente.
Los valores de la entalpía de activación (  ) y la entropía de activación (
) y la entropía de activación (  ) fueron calculados mediante la expresión (12)
) fueron calculados mediante la expresión (12)

Donde los valores de 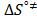 y
y  fueron usando el método de los mínimos cuadrados a partir de la pendiente y el intercepto de la gráfica de
fueron usando el método de los mínimos cuadrados a partir de la pendiente y el intercepto de la gráfica de  en función de T. Los datos obtenidos de
en función de T. Los datos obtenidos de  y
y  se muestran en la Tabla 7.
se muestran en la Tabla 7.
En la Tabla 7 es notorio que los valores de  y
y  son positivos a todas las temperaturas y composiciones de solvente mixto, lo cual sugiere que la formación del estado de transición va acompañado de una disrupción de los enlaces intermoleculares y una estructura más desordenada de las especies en el estado activado.Este comportamiento se ha observado en otros sistemas de aminoácidos en solventes mixtos [5,15,22]
son positivos a todas las temperaturas y composiciones de solvente mixto, lo cual sugiere que la formación del estado de transición va acompañado de una disrupción de los enlaces intermoleculares y una estructura más desordenada de las especies en el estado activado.Este comportamiento se ha observado en otros sistemas de aminoácidos en solventes mixtos [5,15,22]
4. Conclusiones
En este trabajo se reportan los datos experimentales para las viscosidades del sistema Glicina en soluciones acuosas de Tiosulfato de Sodio Pentahidratado (0.01-2.0 mol Kg-1) a las temperaturas de (283.15; 288.15; 293.15; 298.15; 303.15; 308.15; 313.15 y 318.15) K y 101.1 Kpa.
Los valores del coeficiente B son positivos a lo largo de todas las composiciones e isotermas de estudio, lo que sugiere que en el sistema se favorecen las interacciones soluto-solvente, las cuales podrían ser asociadas a dos tipos de interacciones: 1) Interacciones Ión - ión entre el ión Na+ del solvente mixto y el grupo COO- de la Glicina y 2) Interacciones Ión - Ión entre el ión  y el grupo NH3+ de la Glicina. Adicionalmente los valores de
y el grupo NH3+ de la Glicina. Adicionalmente los valores de  y
y  son positivos; hecho que indica que la Glicina actúa como un disruptor de la estructura del solvente (cosmotrópico) y que las interacciones en el sistema pseudobinario son altamente específicas.
son positivos; hecho que indica que la Glicina actúa como un disruptor de la estructura del solvente (cosmotrópico) y que las interacciones en el sistema pseudobinario son altamente específicas.
Por otro lado los valores de 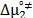 y
y  son positivos y mayores que los valores de
son positivos y mayores que los valores de  ; lo que sugiere que el estado de transición es menos favorecido en presencia de Glicina y que la formación de este estado va acompañado de la disrupción y distorsión de los enlaces intermoleculares en la estructura del disolvente.
; lo que sugiere que el estado de transición es menos favorecido en presencia de Glicina y que la formación de este estado va acompañado de la disrupción y distorsión de los enlaces intermoleculares en la estructura del disolvente.
Finalmente el signo positivo de  y
y  sugieren que la formación del estado de transición presenta una estructura más desordenada de las especies en el estado activado.
sugieren que la formación del estado de transición presenta una estructura más desordenada de las especies en el estado activado.
Agradecimientos
Los autores agradecen a la Universidad de Córdoba, a la Universidad Andres Bello y a la Beca de Doctorado CONICYT Programa Formación de Capital Humano Avanzado/Doctorado Nacional-63130037 por el apoyo prestado para la realización de este trabajo.
Referencias
[1] Páez, M., Cantero, P., and Peña, J., Viscosities of the Mixture N,N-Dimethylformamide +1-Butanol at Different Temperatures. Inf. Tecnol., 23(3), pp.149-156, 2012. [ Links ]
[2] Wang, P., Anderko, A. and Young, R.D., Modeling viscosity of concentrated and mixed-solvent electrolyte systems, Fluid Phase Equilib., 226, pp. 71-82, 2004. [ Links ]
[3] Kumar, A., Molecular interactions in binary mixtures of formamide with 1-butanol,2-butanol, 1,3-butanediol and 1,4-butanediol at different temperatures: An ultrasonic and viscometric study, Fluid Phase Equilibria., 265, pp.46-56, 2008. [ Links ]
[4] Páez, M., Lans, E. and Cantero, P., Densities and volumetric properties of the mixture N,N-dimethylformamide (DMF) + 1-butanol at several temperatures. DYNA, 80(177), pp.132-141, 2013. [ Links ]
[5] Sinha, B., Sarkar, A., Kumar, P., and Brahman, D., Physicochemical properties of L-Alanine in aqueous silver sulphate solutions at (298.15, 308.15, and 318.15) K, Int. J. Thermophys., 32, pp.1-17, 2010. [ Links ]
[6] Ali, A. and Shahjahan, A., Density and viscosity of a-amino acids in aqueous solutions of cetyltrimethylammonium bromide, Russ. Chem. Bull., 59, pp.1999-2004, 2010. [ Links ]
[7] Shekaari, H. and Jebali, F., Solute-Solvent interactions of amino acids in aqueous 1-Propyl-3-Methylimidazolium bromide ionic liquid solutions at 298.15 K, J. Solution Chem., 39, pp.1409-1427, 2010. [ Links ]
[8] Siegel, A. and Siegel, H., Metal ions in biological systems., Inc. New York. USA, 1973. [ Links ]
[9] Williams, R. J., Bioinorganic Chemistry: Trace element aerobic anaerobic evolution In: Structure and bonding, Vol. 91, Springer, 1998. [ Links ]
[10] Fraústo da Silva, J.J.R. and Williams, R.J.P., The biological chemistry of the elements. Oxford University Press. Oxford, 2001. [ Links ]
[11] Jones, G. and Dole, M., The viscosity of aqueous solutions of strong electrolytes with special reference to barium chloride, J. Am. Chem. Soc., 51, pp. 2950-2964, 1929. [ Links ]
[12] Stokes, R.H. and Milles, R., International encyclopedia of physical chemistry and chemical physics, Pergamon Press, New York, 1965. [ Links ]
[13] Yan, Z., Wang, J., Kong, W.,and Lu, J., Effect of temperature on volumetric and viscosity properties of some [alpha]-amino acids in aqueous calcium chloride solutions, Fluid Phase Equilib., 215(2), pp. 143-150, 2004. [ Links ]
[14] Banipal, T.S. and Singh, G., Thermodynamic study of salvation of some amino acids, diglycine and lysozyme in aqueous and mixed aqueous solutions, Thermochim. Acta, 412, pp. 63-83, 2004. [ Links ]
[15] Yan, Z., Wang, J. and Lu, J., Viscosity behavior of some a-amino acids and their groups in water-sodium acetate mixtures, Biophys. Chem., 99, pp. 199-207, 2002. [ Links ]
[16] Banipal, T.S., Kaur, J., Banipal, K., Sood, K., and Singh, K. Volumetric and Viscometric Studies of Some Amino Acids in Aqueous Solutions of Cadmium Chloride at T = (288.15 to 318.15K and at Atmospheric Pressure. J. Chem. Eng. Data, 56, pp. 2751-2760, 2011. [ Links ]
[17] Bhat, R., Kishore, N. and Ahluwalia, J.C., Thermodynamic studies of transfer of some amino acids and peptides from water to aqueous glucose and sucrose solutions at 298.15 K, J. Chem. Soc. Faraday Trans. I, 84(8), pp. 2561-2665, 1988. [ Links ]
[18] Li, Z., Sang, W. and Lin, R., Partial molar volumes of glycine, L-alanine and L-serine in aqueous glucose solutions at T = 298.15 K, J. Chem. Thermodyn., 34, pp.1761-1768, 2002. [ Links ]
[19] Glasstone, S., Laidler, K. J. and Eyring, H., The theory of rate processes, McGraw Hill, New York, 1941. [ Links ]
[20] Feakins, D., Freemantle, D. and Lawrence, K., Treatment of the transition state of the relative viscosity of electrolyte solutions. Applications to aqueous systems, nonaqueous and methanol + water, J. Chem. Soc. Faraday Trans., 1(70), pp.795-806, 1974. [ Links ]
[21] Sinha, A., Kumar, P. and Mahendra, N., Apparent molar volumes and viscosity B-Coefficients of glycine in aqueous silver sulphate solutions at T = (298.15, 308.15, 318.15) K, .Acta Chim. Slov., 57, pp.651-659, 2010. [ Links ]
[22] Khanuja, P., Volumetric and viscometric study of interactions of amino acids in aqueous sucrose solution at different temperatures, Chem Sci Trans.vol. 2(4), pp. 1268-1275, 2013. [ Links ]
M. S. Páez-Meza, Graduado en 1987 como Licenciado en Química en la Universidad de Córdoba. Colombia. En 1996 se graduó de Especialista en Ciencias Física; mientras que en el 2001 se graduó de Magister en Ciencias Químicas, y en 2006 de Dr. Sc Ciencias Químicas, todos ellos de la Universidad Nacional de Colombia. Bogotá, Colombia. Del 1996 a la fecha, se desempeña como docente de carrera en la Universidad de Córdoba tanto en los programas de pregrado como de postgrado. También se desempeña como líder del grupo de investigación: Fisicoquímica de mezclas líquidas.
G. M. Alvarino-Bettín, Graduado como Licenciado en Matemáticas y Físicas en la Universidad de Córdoba en Junio de 1982; recibió título de Especialista en Ciencias Físicas en Agosto de 1997 en la Universidad Nacional de Colombia, sede Bogotá en Agosto de 1997; recibió título de MSc en Ciencias Físicas en la Universidad Nacional de Colombia, sede Bogotá en octubre de 2002; recibió título de Magíster en Educación en la Universidad de Córdoba, en Diciembre de 2008. Desde 1982 hasta 1997 se desempeñó como docente de secundaria en el sector público, en diferentes instituciones del Departamento de Córdoba. Desde 1997 se vinculó como docente de planta a la Universidad de Córdoba, adscrito al Departamento de Física y Electrónica, desempeñándose como docente investigador en el área de percepción remota satelitaria, trabajando con digitalización de imágenes de satélite. Posteriormente trabajó en proyectos de investigación en el área de física médica. En la actualidad trabaja en proyectos que se enfocan en el estudio de la termodinámica de soluciones acuosas, en colaboración con docentes del Departamento de Química en la Universidad de Córdoba.
P. de los S. Cantero-López, Graduado como Químico en Diciembre de 2009 y Magister en Ciencias Químicas en marzo de 2014 en la Universidad de Córdoba Colombia. Desde 2007 se desempeña como investigador al grupo de investigación: Fisicoquímica de mezclas líquidas. Desde 2010 hasta 2012 se desempeñó como docente en la Universidad de Córdoba. Actualmente es estudiante del Doctorado en Fisicoquímica Molecular en la Universidad Andrés Bello (Santiago de Chile).