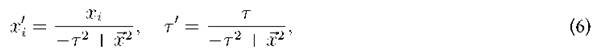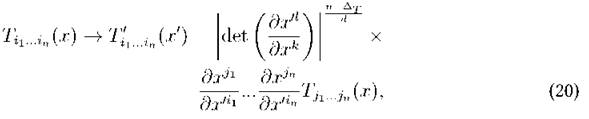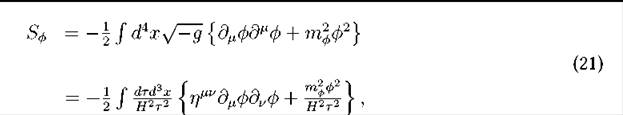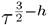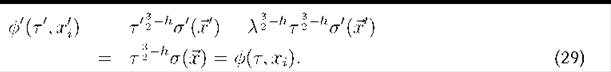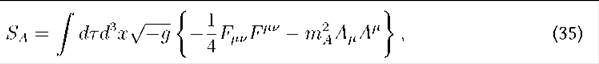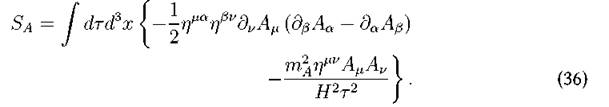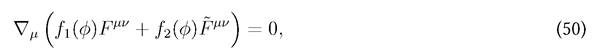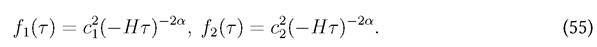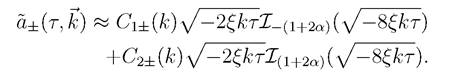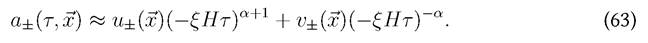Introduction
The study of the symmetries is very important when we look for fundamental descriptive features of a particular physical system and solve its dynamics. For example, it is well known that through the Noether theorem we can identify conserved quantities related to the symmetries, which allows us to discover intrinsic fundamental characteristics that will be reflected on the dynamics of the system. It is also well known that the geometry of the inflationary period of our universe is described with great accuracy by the de Sitter space.
This spacetime is similar to the Minkowski spacetime in the sense that it is a maximally symmetric space, which means that in D dimensions, the number of symmetry generators is D(D + 1)/2. This fact defines and restricts the form of the kinematic features and the evolution of a system on this space. During the inflationary period, the symmetries of the de Sitter group play an essential role on the description of the primordial perturbations and their statistical properties.
In particular, by using the correspondence between the de Sitter symmetry group in D-dimensions and the conformal group in an euclidean (D - 1)- dimensional “boundary” space (Strominger, 2001), it is possible to calculate general important features of the system, such as the correlations functions of the fields that govern the dynamics of the inflationary Universe (Biagetti et al., 2013), which are necessary to calculate the statistical descriptors of the primordial curvature perturbation by using, for example, the bN formalism (Sasaki & Stewart, 1996; Nakamura & Stewart, 1996; Starobinsky, 1985; et al., 2005; Dimopoulos et al., 2009) or cosmological perturbation theory (Gumrukcuoglu et al., 2010; Bartolo et al., 2013). To do that, we need first to calculate one of the fundamental quantities of the conformal field theory description: the conformal weights of the fields.
The correspondence between a field theory in de Sitter space and a dual theory in a euclidean boundary space (one dimension less than the de Sitter space) is what we shall refer to as dS/CFT correspondence and it is at the core of the approach that we are pursuing here. This correspondence was proposed initially for free non interacting single fields propagating on de Sitter space (Bousso et al., 2002) but some considerations about the interacting case was discussed in the literature (Spradlin & Volovich, 2002)
In this paper, we follow the approach proposed by (Biagetti et al., 2013) to study the case of a coupled scalar-vector system. In the context that we are framing our discussion, the scalar field is responsible for the inflationary expansion and the vector field is partly responsible of the generation of the primordial curvature perturbation ζ. The inclusion of vector fields on the inflationary dynamics permits the study of several interesting possibilities such as the presence of statistical anisotropies, parity violating patterns, the origin of primordial magnetic fields, etc. (see for instance Caprini & Sorbo, 2014; Maleknejad et al., 2013; Soda, 2012; Dimastrogiovanni et al., 2010, and references therein). For concreteness, we will settle the discussion in four dimensional de Sitter space but the results obtained can be generalised straightforwardly to any dimensions.
This paper is organized as follows. In section II, we review the symmetries and some basics of de Sitter space. Next, in sections III and IV, we shall describe the transformation laws imposed by these symmetries over the conformal fields on the dual theory and we calculate the associated conformal weights of those fields. In section V, we briefly review the results for the scalar and the vector field separately and then, in section VI, we consider the coupled scalar-vector system. Finally, in section VII, we present our conclusions and discuss some possible applications of the results obtained.
Symmetries of the de Sitter Space
The de Sitter spacetime can be described in several useful coordinate systems (for reviews see for instance Spradlin et al., 2001 and Leblond et al., 2002), but for our interests, we will chose the 4D conformal planar coordinates in which the line element is written as
where H is the Hubble parameter and t is the conformal time. In this coordinate system, it is easy to see that the line element is invariant under spacial translations and rotations on T = constant sections:
where αi is a 3-dimensional constant vector and Rij is an O(3) matrix satisfying the condition Rik Rkj = δji and representing a three dimensional rotation. We have a total of six symmetry generators included in the transformation and they affect only the spacial sections of the spacetime.
Also, notice that we allow the possibility of spacial reflexion xi → - xi in this group of transformations. Spacial reflexion is an explicit symmetry of the line element and we will pay attention to this specific transformation, when we consider the possibility of introducing parity violating models in the presence of vector fields. There are two additional transformation which mixes the time and the spacial coordinates, the spacetime dilatation:
where A is a constant factor and the special conformal transformation:
and
with bµ = (0, bi) a three dimensional vector which generates the transformation.
In the last expressions we use the notation x 2 = ηµvxµxv, ηµv=diag(-1, 1, 1,
1), → x 2 = δij xixj and → x . →b = δij bixj. Together, the transformations),) and tell us that de Sitter space has ten symmetry generators. This is a maximally symmetric spacetime. It can be seen that is constructed out by the composition of three consecutive transformations, namely, an inversion, written as
or
then a translation (T' ^ T" = T' and x’i ^ x”i = x’i + bi) and then an inversion again. Actually, the special conformal transformation can be expressed as:
It becomes useful in the following to have the Jacobian matrices associated to the coordinate transformations of the de Sitter isometries. Particularly, we will need the Jacobian for the dilatation and for special conformal transformation and . Nevertheless, as we said before, the special conformal transformation can be obtained by composing translations and inversions, allowing us to use the transformation instead of .
The Jacobian matrix of the inversion, can be derived directly for obtaining
where  satisfies the orthogonality relation
satisfies the orthogonality relation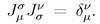 . The associated Jacobian determinant of the above transformation is
. The associated Jacobian determinant of the above transformation is
Using , we can also calculate the Jacobian of the inverse transformation x'→x, obtaining
On the other hand, for the dilatations we have:
Then, with the previous results, we can also calculate the change in the volume element, which reads:
In next sections, we will exploit the correspondence between the de Sitter isometry group represented by the transformations below and the conformal group in  . In the essence of this correspondence lies the idea that de Sitter isometries act as the conformal group transformations in
. In the essence of this correspondence lies the idea that de Sitter isometries act as the conformal group transformations in  , a fact that we will show on next section. Particularly, we will consider the asymptotic region, where inflationary perturbations are frozen, after horizon crossing at supper Hubble scales which in these coordinates happens for
, a fact that we will show on next section. Particularly, we will consider the asymptotic region, where inflationary perturbations are frozen, after horizon crossing at supper Hubble scales which in these coordinates happens for 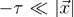 . Then, in the following section, we will recall some basis of the conformal group and introduce the relevant terminology that will allow us to construct a conformal field theory representation of the fields in de Sitter space.
. Then, in the following section, we will recall some basis of the conformal group and introduce the relevant terminology that will allow us to construct a conformal field theory representation of the fields in de Sitter space.
An important part of the following discussion is devoted to the conformal weight of the fields in the conformal field theory representation. The conformal weight of the field is a crucial element for expressing the transformation rules of the fields and the symmetries of their correlation functions which are the meaningful objects constructed in the theory because they encode the statistical properties of the theory.
Conformal group basics and relation with de Sitter group symmetries
In an Euclidean space, the conformal group is defined as the set of coordinate transformations x→x’ that leave invariant the angles between two vectors in this space, or, equivalently, the group of transformations that leave invariant the metric up to a factor
where w(x) is an arbitrary function of the coordinates. It is easy to see that the transformations , and act as conformal transformations on  for the euclidean metric, i.e. gij = δij, in with the corresponding conformal factor w:
for the euclidean metric, i.e. gij = δij, in with the corresponding conformal factor w:
Then, we can see explicitly that the de Sitter symmetry group in four dimensions induces a conformal group in the three dimensional space. In few words, we can interpret the symmetries to as the asymptotic symmetry group of the boundary region of the four dimensional de Sitter space time. In our context, the asymptotic region is located at super horizon scales when the inflationary perturbations evolve classically and carry the information of the physical mechanism that drives the inflationary expansion. In the coordinates employed here, and in the previous expressions, we have used that the super horizon limit which constitutes our asymptotic euclidean space lies in the region  . It its worth to notice that we obtain ten symmetry group generators as we expect for the conformal group acting on three dimensional space.
. It its worth to notice that we obtain ten symmetry group generators as we expect for the conformal group acting on three dimensional space.
Additionally, or equivalently to the expression we can write the inversion transformation and its associated conformal factor as:
So far, we were talking about the symmetries and the geometry of the spacetime, and now we turn to the fields on the theory. The relevant objects that we need for the conformal field theory description, are the ones that we shall call a primary field. A primary field is an object which transforms according to the following rule under conformal transformations
where n is the order of the tensor, d is the dimension of the spacetime and ΔT is the conformal weight of the field (Biagetti et al., 2013). When dealing with the conformal dual theory to the theory in de Sitter space, we will consider the Euclidean space  .
.
By using the above transformation, we can find the conformal dimension AT of different fields that are involved in the theory. It is beyond the scope of this short article to enter in the details of the conformal field theory machinery, so we will just restrict to the introduction of the fundamental elements necessary for our purpose. A complete study of conformal field theory can be found for instance in (Ginsparg, 1988)
Fields on de Sitter space
Now, we will study of fields propagating on de Sitter space. With the results obtained in the previous section, we can evaluate the conformal weight, which is an essential quantity necessary for the conformal field theory description of the fields. We are interested in the coupled scalar vector system, but, before that, and mainly for illustrative reasons and for developing the technique introducing the necessary elements, we study the single scalar field and the single vector field cases separately. After that and invoking the results from the single field case, we will face the coupled system.
Single scalar field. The action for a single massive scalar field propagating on de Sitter space in the coordinates is given by
Where mՓ is the mass of the Meld. Now, we study the symmetries of the theory in order to learn about the transformation of the elds. To emphasise the dierence between the properties of the scalar eld in de Sitter space and in  , let us suppose that we write the transformation law for a scalar in de Sitter as in (20):
, let us suppose that we write the transformation law for a scalar in de Sitter as in (20):
Demanding invariance of the action SՓ = S’Փ we see that it is necessary to set ΔՓ = 0, and then Փ’= Փ. It is easy to arrive to the same result if we apply the dilatation and it is trivial for the translations and three dimensional rotations because the transformation matrix is orthogonal. Certainly, this result does not come as a surprise at all, since we are talking about of a scalar field. Nevertheless it is worth to stress this fact because we are going to see that asymptotically, in the super horizon limit the dual field associated to the scalar transform according with with a conformal weight different than ΔՓ = 0.
Now, we study the behaviour of the associated conformal field of the scalar filed in the three dimensional space  . To this end, it is necessary to solve the equation of motion and go to super horizon scales. The equation of motion derived from (21) is
. To this end, it is necessary to solve the equation of motion and go to super horizon scales. The equation of motion derived from (21) is
To solve this equation, we go to momentum space. Using the Fourier transform  of the field, the resulting equation is:
of the field, the resulting equation is:
which can be fully solved analytically in terms of Bessel functions Jv and Y v:
where C1 and C2 are constants which depends on boundary initial conditions and
Now, we need the behaviour of the solution at super horizon scales, which in momentum space are achieved when (Tanhayi, 2014). By expanding the Bessel functions in that regime and going back to
(Tanhayi, 2014). By expanding the Bessel functions in that regime and going back to  space, we arrive to
space, we arrive to
where we have separated explicitly the time depending part. The precise interpretation of the previous result depends on the value of the discriminant because depending if  . We can provide a unitary interpretation of the conformal field theory associated, we don’t enter into this discussion here which is beyond the scope of this paper and address the attention of the reader to Strominger (2001), Bousso et al. (2002) and Spradlin & Volovich (2002). In the following, we restrict ourselves to the case
. We can provide a unitary interpretation of the conformal field theory associated, we don’t enter into this discussion here which is beyond the scope of this paper and address the attention of the reader to Strominger (2001), Bousso et al. (2002) and Spradlin & Volovich (2002). In the following, we restrict ourselves to the case  . The dominant solution for super horizon regime in this case is
. The dominant solution for super horizon regime in this case is
The field σ is the one that we need to construct the dual conformal theory for late times after horizon crossing, so, we need to determine if it behave as a conformal field by deriving its transformation under conformal transformations in  , actually, as we comment before, we just need the transformation for dilatations and inversions in 3D. Before that, we need to take the super horizon limit
, actually, as we comment before, we just need the transformation for dilatations and inversions in 3D. Before that, we need to take the super horizon limit 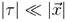 of the inversion :
of the inversion :  . Using Փ' = Փ, and we obtain
. Using Փ' = Փ, and we obtain
which implies:
On the other hand, for inversions in the super horizon regime
which implies:
When we compare and with (with n = 0 and d = 3) we conclude that the field a behaves as a conformal field with conformal weight
This is an important result given that the correlating functions of a conformal field theory can be calculated if we know the conformal weight of the primary fields. In this case, we expect that the 2 point correlating function of the dual theory of a scalar field on de Sitter space behave like
with A a constant. For an detailed analysis of the two point correlation functions in the dual theory see e.g. Strominger (2001) and Leblond et al. (2003).
Single vector field. Now, we turn to the vector field case. We consider a massive vector field with Lagrangian
where Fµv= ∂µAv - ∂vAµ and mA is the mass of the vector field. This model have been studied with some detail in Ackerman et al. (2007) and (allowing for non-minimal coupling) Golovnev et al. (2008) and in that time, it sparked some interest in the study of inflationary models with vector fields. In de Sitter conformal coordinates we have the action
Again, as we did in the scalar case, we will consider that Aµ transforms as in in the following way
and using inversion we get the transformation of the action with respect to the change of coordinates
from which we deduce that invariance under inversions implies that ΔA = 1. Again, this is not surprising since this is precisely the transformation law for a vector in four dimensional de Sitter space.
Now, we look if there is an associated three dimensional vector which transforms as a conformal vector field in  . We begin by solving the equations of motion derived from the action
. We begin by solving the equations of motion derived from the action
The system before propagate three degrees of freedom due to the presence of the mass term, two transverse terms perpendicular to the propagation axis, and a longitudinal term for the equation of the component A0. It is well known that the longitudinal mode in this model is problematic due to the presence of ghost instabilities (Himmetoglu et al., (2009a); Himmetoglu et al., (2009b)), but it is also known that this problem can be solved by introducing a time dependent coupling in the Maxwell term f (T)F2 and a time dependent mass term m(T) (Dimopoulos et al., (2010a); Dimopoulos et al., 2010b)).
We avoid the analysis of the longitudinal mode which is not relevant for our main objectives here, we refer the reader to the references mentioned before and in the following we just focus on the transverse components that can be obtained from the divergence free spacial components (∂iAi = 0) :
Again, in a similar way that in the scalar case, we solve the equation for the transverse component in momentum space
where Ấi is the Fourier transform of the vector field, and
Going to super horizon scales at  and going back to coordinates space we get the asymptotic expansion
and going back to coordinates space we get the asymptotic expansion
For late times, again we have that the dominant term is  , then:
, then:
And we consider the asymptotic symmetries of dilatations and inversion. The result is the same for both symmetries as in the scalar field, and then we only show the transformation law of the boundary field Ui under dilatations.
Taking into account the transformation law for the vector field:
which for dilatations become A'1 = λ-1Ai. Then we can see that
so, Ui transforms as
which, comparing with implies that U fulfil our expectations and behave precisely as a conformal vector field in  under the asymptotic symmetries of de Sitter group with conformal weight
under the asymptotic symmetries of de Sitter group with conformal weight
We learned in previous sections that in the spirit of the so called dS/CFT correspondence, free fields propagating on de Sitter admit a dual conformal field theory representations in the boundary of the space which we take to be a  space placed at the super horizon limit, this is at
space placed at the super horizon limit, this is at  . We have calculated the conformal weight of the corresponding conformal fields correspondence which are essential for the calculation of correlation functions and to describe the statistical properties of the theory. Although the results presented in the previous sections where obtained for free fields, there are several discussions in the literature which points towards of an extension of this correspondence also in the presence of self interactions and for coupled systems involving several fields. In next section we discuss coupled system involving a scalar and a vector field which results useful for applications in inflationary cosmology and analyse in which conditions it is possible to extend the ideas explored in previous sections and if it is possible to find a conformal field theory representation of the theory aiming to calculate the properties of inflationary perturbations by using the conformal field theory machinery.
. We have calculated the conformal weight of the corresponding conformal fields correspondence which are essential for the calculation of correlation functions and to describe the statistical properties of the theory. Although the results presented in the previous sections where obtained for free fields, there are several discussions in the literature which points towards of an extension of this correspondence also in the presence of self interactions and for coupled systems involving several fields. In next section we discuss coupled system involving a scalar and a vector field which results useful for applications in inflationary cosmology and analyse in which conditions it is possible to extend the ideas explored in previous sections and if it is possible to find a conformal field theory representation of the theory aiming to calculate the properties of inflationary perturbations by using the conformal field theory machinery.
Vector-scalar coupled system. In this section we study a system of interacting scalar and vector fields which results useful for several applications to inflationary cosmology (Ratra, 1992; Dimopoulos et al., 2010a; Watanabe et al.,2010; Dimopoulos et al., 2010b; Wagstaff & Dimopoulos, 2011; Barnaby et al., 2011; Sorbo, 2011; Dimopoulos & Karciauskas, 2012; Anber & Sorbo, 2012; Bartolo et al., 2013; Lyth & Karciauskas, 2013; Shiraishi et al., 2013; Cook & Sorbo, 2013; Nurmi & Sloth, 2014; Caprini & Sorbo, 2014; Chen et al., 2014; Bartolo et al., 2015; Namba et al., 2016). The model that we consider here is described by the action
In the second term, 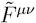 is the Hodge dual of the field strength
is the Hodge dual of the field strength  and is defined by
and is defined by
where Єµvαβ is the four dimensional Levi-Civita symbol and  and
and  are coupling functions which depend only of the scalar field. This model introduces explicitly parity violation through the term
are coupling functions which depend only of the scalar field. This model introduces explicitly parity violation through the term  . We assume the results obtained previously for the conformal weight of the scalar and the vector field in four dimensional de Sitter ΔՓ = 0 and ΔA = 1, so the action is manifestly invariant under de Sitter group transformations. Additionally, assuming Δfi = 0 imply that if we assign some conformal weight Af to the coupling functions
. We assume the results obtained previously for the conformal weight of the scalar and the vector field in four dimensional de Sitter ΔՓ = 0 and ΔA = 1, so the action is manifestly invariant under de Sitter group transformations. Additionally, assuming Δfi = 0 imply that if we assign some conformal weight Af to the coupling functions
we get that Δfi = 0 in order to preserve de Sitter invariance.
Now, we solve the equations of motion and study its super horizon evolution. In the context that we frame the discussion we consider that the scalar field drives the inflationary dynamics and that the vector field is an auxiliary subdominant field which affects the primordial curvature perturbation and can leave an imprint on the inflationary evolution. The scalar affect the evolution of the vector field through the coupling functions 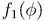 . The equations of motion for the vector field derived from the action are:
. The equations of motion for the vector field derived from the action are:
which must be complemented with the Bianchi identity:
We don’t solve the dynamics of the scalar field, we just assume some features of its solutions due to the fact that this field drives the inflationary expansion. Accordingly, we further assume that the inflationary dynamics homogenise the scalar perturbations, so that we can approximate the scalar field as a time dependent function, this is ∂iՓ = 0. Accordingly, this implies that on the solutions of the inflationary scalar field 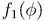 =
= and
and  =
= , then ∂if1 = ∂if2 = 0. With this approximation, the temporal and spacial components of the equation in de Sitter conformal coordinates becomes respectively
, then ∂if1 = ∂if2 = 0. With this approximation, the temporal and spacial components of the equation in de Sitter conformal coordinates becomes respectively
and
Given that this theory is manifestly gauge invariant because it only depend of the field strength  and its dual
and its dual  , we choose the Coulomb gauge and set A0 = 0 and ∂iAi = 0. With this choice, the temporal equation cancels and the spatial part reduces to:
, we choose the Coulomb gauge and set A0 = 0 and ∂iAi = 0. With this choice, the temporal equation cancels and the spatial part reduces to:
So far, we don’t have any restriction over the form of the coupling functions fi, and now we impose some conditions mainly, to preserve conformal invariance on the asymptotic region. Let’s apply the dilatation  to the previous equation and demand invariance under this transformation. We further assume that the coupling functions are homogeneous functions of time, this is
to the previous equation and demand invariance under this transformation. We further assume that the coupling functions are homogeneous functions of time, this is  , so that the equation of motion transforms as:
, so that the equation of motion transforms as:
In this way we see that a necessary condition for getting scaling invariance is that the coupling functions are homogeneous functions of the same order n = m. This is achieved if the couplings are power law functions proportional to each other:
which implies that
In the previous expression, we restored the Hubble constant for dimensional analysis. Let us reuse n = - 2α because the function f must be positive due to hamiltonian stability. In order to avoid strong coupling at super horizon evolution, we assume that α < 0
Now, let’s follow the analysis in terms of the normalized canonical field ai defined as
For the canonical field ai, the equation of motion is written as
and using gives:
Now, we go to Fourier space. Choosing k = (k, 0, 0) and defining the transverse polarizations as
we get
The equation can be solved analytically in terms of regular and irregular Whittaker functions W and M:
where the parameter  defined in Caprini & Sorbo (2014) determine the relative size of the parity violation signals in the model. Reference Caprini & Sorbo (2014) study in full detail the features of the model with
defined in Caprini & Sorbo (2014) determine the relative size of the parity violation signals in the model. Reference Caprini & Sorbo (2014) study in full detail the features of the model with 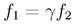 and describe analytically its asymptotic behaviour. For scales in which
and describe analytically its asymptotic behaviour. For scales in which  , the W function dominates and we will consider only its contribution. Morover, if we take
, the W function dominates and we will consider only its contribution. Morover, if we take in we have solutions in terms of modified Bessel functions of the first kind :
in we have solutions in terms of modified Bessel functions of the first kind :
Which, in particular, for super horizon scales in which we have
we have
We can write the last equation as
in which we restored H and absorbed further dependence of k, ξ, α in the U and  functions. At this point, we go back to coordinates space obtaining the asymptotic form:
functions. At this point, we go back to coordinates space obtaining the asymptotic form:
We have succeed on separating the time and space coordinates for super horizon scales, so, we can assign a conformal boundary field in this case as in the previous cases studied. This situation is nevertheless a bit different given that the dominant term depends on the value of the exponent α, if α > -1/2 the term v± dominates, while, if α < -1/2 the term u± is the one that dominates. If α > -1/2, we demand that
while, if α < -1/2 we take the boundary condition
Now, we can calculate the conformal weight of those boundary fields applying the same procedure of previous sections. We only consider the dilatation transformation, the inversion is entirely analogous. We see that the canonical field a± transforms under four dimensional dilatations ,
,  as a four dimensional vector with weight Δα = 1:
as a four dimensional vector with weight Δα = 1:
Applying dilatation over we have:
which implies
and comparing with with n =1 and d =3 we conclude that the boundary field v± behave as a conformal field of weight:
Following the same procedure we find that the boundary field behaves as a conformal boundary field of weight
To summarise, we have obtained that the interacting system admit a conformal field theory representation at super horizon scales through the boundary vector fields u± , v±. A remarkable fact of this results is that they coincide with the case studied in Biagetti et al. (2013), where they studied the model without parity violation term, this is
Naively, we could think that both cases, the parity conserving and the parity violating models have the same conformal boundary field associated and that the statistical features of the theories given by the correlating functions are the same. Nevertheless, there is a crucial difference implied by the fact that the super horizon boundary symmetry group allow the spacial reflection  as an element of the symmetry group. In this case, the correlating functions allow for antisymmetric terms in its structure, for instance, the power spectrum of a boundary field would be
as an element of the symmetry group. In this case, the correlating functions allow for antisymmetric terms in its structure, for instance, the power spectrum of a boundary field would be
where the form of the βi functions can be determined by using the asymptotic symmetries of the theory (Biagetti et al., 2013). It is important to see that the functions β2(k) and β3(k) are related to anisotropic and to parity violating effects respectively. In the parity conserving case (β3 = 0), the above equation can be written as
If we assume that the vector field points along the direction of some unit vector n and the wave vector k points along the unit vector k, the power spectrum can be written as (Ackerman et al., 2007):
where β(k) is the isotropic power spectrum and g(k) is a function measuring the amount of statistical anisotropy. If g(k) is scale invariant, recent data analysis gives an upper bound on that: g < 10-2 (Kim & Komatsu, 2013; Ade et al., 2016).
A further development of this ideas on the calculation of the correlation functions using conformal field theory techniques exploiting the asymptotic symmetries as presented in Biagetti et al. (2013) for the case of parity violating theories have enough interests and we expect to pursue this possibility in future work.
Conclusions
In this paper, we have comprehensively studied the symmetry properties of the scalar and vector fields solutions on de Sitter space. We study their asymptotic limit at super horizon scales and we found that, in this limit, free fields behave as conformal fields on a constant time surface. We study the free scalar and the free vector fields for pedagogical purposes, to illustrate the technique and then study an inflationary model with interacting scalar and vector fields.
The coupled system is studied because it is interesting for its cosmological implications, in particular this kind of model can explain some observable CMB anomalies such as broken of inversion and rotational invariance. The super horizon scales are important in our context because inflationary expansion freeze the perturbations at this scales and the correlation functions, evaluated at this scales, carry information from the inflationary dynamics. In this sense, the use of the asymptotic conformal symmetries of de Sitter space offers a powerful technique to uncover the structure of the correlations, which relies only of the conformal weight of the boundary asymptotic fields.
Regarding the specific scalar-vector model studied, we can mention two important aspects, the first one is that the coupling functions 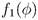 and
and  in Eq. fulfill the condition
in Eq. fulfill the condition  and the second one is that if we assume that the functions are a power law on
HT
(which is a good choice because we are looking for an homogeneous universe), the conformal weight of the vector fields on super horizon scales depend only of that power (see Eqs. and ). This result is according with the one obtained by Biagetti et al. (2013), who studied the parity conserving case with
and the second one is that if we assume that the functions are a power law on
HT
(which is a good choice because we are looking for an homogeneous universe), the conformal weight of the vector fields on super horizon scales depend only of that power (see Eqs. and ). This result is according with the one obtained by Biagetti et al. (2013), who studied the parity conserving case with  0. Our next step is to use the conformal weight of the boundary vector field to calculate the shape of the correlation functions following the procedure given by Biagetti et al. (2013) and identify the signals of parity violation.
0. Our next step is to use the conformal weight of the boundary vector field to calculate the shape of the correlation functions following the procedure given by Biagetti et al. (2013) and identify the signals of parity violation.