Introduction

Epidemiological research, in the field of visual health, strives continuously to find new knowledge and new methods of analysis based on studies performed on populations of individuals. The data collected from such studies should be susceptible of analysis with the appropriate statistical tools on the assumption that such data are trustworthy.

Ametropias are considered spherical when the Principal Meridians have the same refractive power, otherwise they are considered astigmatic ametropias. In the case of spherical Ametropias, their magnitudes provide sufficient information to appraise its severity and diagnose and prescribe the corresponding correcting lenses. This is not the case in astigmatic ametropias. An astigmatism of, say, 2,50 diopters, does not provide enough information since it only represents the difference between the Principal Meridians but fails to identify the nature and magnitude of the underlying Ametropia.

Spherical ametropias are easily classified as low, median and high, regardless of whether they are myopic or hyperopic. Astigmatic ametropias, on the contrary, are classified in many ways such as location of principal meridians relative to the retina; the location, vertical or horizontal, of the most affected meridian; the frequency of a given orientation of astigmatism in the general population; the quality of the corneal surface, and the harmony of astigmatisms in the two eyes.

In clinical practice, measuring an Ametropia and its visual acuity, usually constitutes enough information to establish diagnosis of the refractive state including severity of symptoms and proper disposal of patient. A very different situation arises when dealing with epidemiological studies in which you must handle large numbers of refractive data.

Any research on any field of science, may need several tools for analysis such as description of variables, comparison of samples, variance analysis, correlations, regressions, Z tests, t tests, etc.¹ Whatever the case, clarity and precise definition of data and tools are required. It is necessary, therefore, to have an Index or Indicator, that condenses in a single number, any refractive state, spherical o astigmatic, and summarizes all variables to severity and serves as guide to define proper clinical and general visual health actions that can apply to the general population.

According to The Free Dictionary "an Index is a number, that results from a formula, that is used to characterize an array of data and permits drawing conelusions".²

There are many indexes in medicine to evaluate diverse types of situations, e.g.: Apache I and II for disease classification, Triage guide for Hospital Emergency Units, ICU patient care, evaluation of disasters, medical classification for specific diseases according to severity. All these indexes are based on objective physiological measurements independently of therapeutic guidelines and they are intended to maximize the effectiveness of patient care and, to diminish wasted efforts and resources.

The proper use of statistics in ametropias, before and after any intervention, has always been a problem. The combination of "spheres" and "cylinders" is more complex than generally thought since the cylindrical component of astigmatic ametropias represents a dioptric difference between the principal meridians and not an ametropic entity like myopia or hyperopia. Some of the alternatives currently used by researchers to perform statistical analyses are the following:

Recently, Merchán and Merchán³, classified ametropias into categories according to severity with a purely clinical criterion. Severity was taken as the degree by which a refractive error jeopardizes the ability of a person to function in everyday life. Categories of Ametropias are amenable to statistical analyses by non-parametric methods.

Holladay⁴, pretended to evaluate the relation between refractive error, visual acuity and pupil size, in patients after radial keratotomy. For that purpose, He proposed the Defocus Equivalent consisting of adding the absolute value (+) of half the cylinder to the absolute Spherical Equivalent in case of myopia (-) or hyperopia (+) under cycloplegia. He only gives one example of his DE. Keating⁵ in 1980, deals with the use of matrices for adding spherocylindrical lenses in the case of a patient wearing some prescription that needs to be modify by over-refraction procedure.

Later, Keating⁶ in 1983, illustrates the "use of matrices for the mean value of refractive errors" emphasizing the advantage of the dioptric power matrix which plays the same role for spherocylindrical lenses as the dioptric power plays for spherical lenses. His equations allow to convert spherocylinders into matrices which, in turn, can be added and averaged. Harris, in 1988⁷, using Long's equations, shows the Refractive Surgical Effect of various surgical procedures by means of matrices to represent spherocylinders. He also mentions, but does not dwell into, the possibility of statistical analyses.

Long⁸, in 1991, develops matrices to represent sphere, cylinder and axis of conventional prescription lenses and adding the traces of two or more power matrices, the equivalent sphere is obtained. Kaye⁹ later in 2002, describes how matrix algebra can represent sphero-cylinders and refractive errors and in so doing, sphero-cylinders can be added, subtracted, multiplied, inverted and raised to powers.

Thibos¹⁰ based their investigation on Fourier analysis of the three elements of astigmatism. Spheres, cylinders and axes of multiple ametropias are converted into power vectors that are then, subjected to statistical analyses to finally convert the results back into sphere, cylinder and axis notation. Miller,¹¹ follows the same approach to illustrate how to obtain an average refraction from multiple cases of ametropias. Gartner12, provides the mathematical formulae to calculate cylinder vectors. Raasch13, correlates visual acuity with the vector length of sphero-cylinders and found a significant correlation between spherical myopia, compound myopic astigmatism and mixed astigmatism.

Material and Methods

When the Principal Meridians of the eye are taken as legs of a right triangle, the hypotenuse of such triangle can be determined. Such hypotenuse will represent the refractive state of the eye with a single number that embraces all possible variations of ocular refraction. We call it Index of Ametropia. To validate it, it must have a significant correlation to Visual Acuity since ametropias are the principal cause of blurring of images on the retina (defocus). Considering that Snellen fractions are not real mathematical expressions, ⁽⁸ Snellen Visual Acuity has been substituted by the widely used Log of the Minimum Angle of Resolution (LogMAR). If the Index of Ametro-pia increases, LogMAR increases and visual acuity decreases.

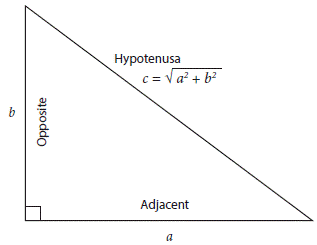
In the illustration (Fig. 1) we see a right triangle in which a and b are called the sides (catheti) and c the hypotenuse. The sides are independent and perpendicular from each other, thus, the magnitude of one side does not affect the magnitude of the other. The hypotenuse on the contrary, is not independent and its magnitude is determined by the magnitude of both sides. This characteristic of the hypotenuse is precisely the reason to assimilate it as Hypotenuse of Refraction which is also dependent, in a similar fashion, to the independent Principal Meridians of the ocular refraction perpendicular to each other.

Figure 1 Right Triangle. a and b are the sides (catheti) and c is the Hypotenuse. 

Pythagoras Theorem simply states that the square of the hypotenuse is equal to the sum of the squares of the sides.

Hypotenuse² = side a² + side b²

Thus, Hypotenuse = √ (side a² + side b²)

Applying the same principle to the ocular refraction, we can write:

Hypotenuse of Refraction ² = Primary Meridian² + Secondary Meridian²

and Hypotenuse of Refraction = √ (Primary Meridian²+Secondary Meridian²)

Example: Given: Rx: + 3.00 sph (-1.25 cyl axis 0°), thus,

Primary Meridian: +3.00 Dpts. Secondary Meridian: +1.75 Dpts.

Index of Ametropia = √ (+3.002 + 1.752) = 3,47

Since the Index of Ametropia is determined by adding the square of each of the Principal Meridians, which turns them all positive, followed by the square root of the total, it becomes irrelevant whether refractive data comes from the spectacle correction of the Ametropia or from the dioptric powers of the refractive error. Hyperopic and myopic ametropias have the same Index of Ametropia since both have the same defocus and the same circle of diffusion provided accommodation is at rest.

In relation to the cylinder Axis, it must be said that it has no bearing on the severity of ametropias and need not be included in statistical studies of visual and refractive conditions. An axis at 180° is no more significant than axis at 60°. The axis becomes important only when the object of interest is formed by horizontal, vertical or oblique components, such as print letters or city buildings. Otherwise, it is not important when observing landscapes or other objects devoid of linear elements. However, it does have a key role in prescribing lenses to correct astigmatic defects.

3964 patients from a database of OP-TILASER (Refractive Surgery Center in Bogotá Colombia) for the year 2014 were selected to demonstrate the applicability of the proposed Index of Ametropia. The patients had not been previously subjected to any kind of surgical procedure. Optometric evaluations were conducted by Carmen Cecilia Villa, optometrist of the Institution.

Another example to illustrate the applicability of the proposed Index of Refraction comes from a database of an investigation "Madre Canguro Integral" (Integral Kangaroo Mother), carried out between 2013 and 2014 at Hospital San Ignacio, Bogotá in which 311 healthy prematurely-born babies were evaluated. The general Objective was to describe the development of premature babies by obtaining the normative values for a test based on Bayley scales for development of breast-feeding infants (3rd edition) and a test based on Griffiths scales of mental development (revised edition) at 3, 6, 9 and 12 months corrected gestational age.

As part of such investigation, optometric refraction was performed at 3 and 9 months to find possible relationships between whole development and visual development of the child. It is, at this point, where the Index of Ametropia can be used to determine media, median, mode and standard deviation of the ametropias involved at 3 and 9 months of age.

Type of Statistical Analysis: Quantitative, descriptive and correlational.

Results

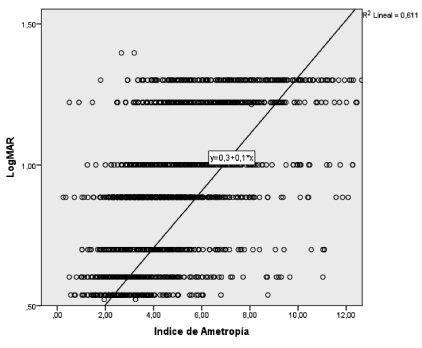
Descriptive Statistics for the Index of Ametropia and LogMAR are shown in Table 1 and table 2. Skewness and Kurtosis for Index of Ametropia clearly show an abnormal distribution whereas

Table 1 Statistics of the sample 

Table 2 Correlation between Index of Ametropia and LogMAR 

Skewness and Kurtosis for LogMAR indicate nearly normal distribution. Consequently, correlation between those variables must be tested by Spearman's rho rather than Pearson's r. Correlations higher than 0,4 are considered high. In our case rho is 0,834 indicating a very high correlation (near perfect). R ² is 0,695 meaning that 69,5% of LogMAR findings are directly correlated to Index of Ametropia. The remaining 30,5% shows the influence of accommodation exerted by hyperopes, among other factors.

Figure 2 Regression: Index of Ametropia and LogMar 

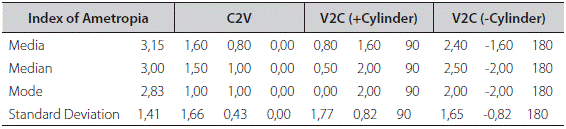
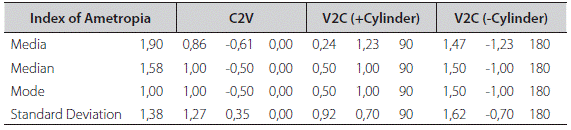
A comparison between the Index of Ametropia and Power Vector methods is shown in Table 3 and 4 which deals with the evolution of refractive state in premature babies at ages 3 months (294 eyes) and 9 months (329 eyes). The first column, Index of Ametropia, shows the results for media, median, mode and standard deviation of the data (data not shown). The second column shows results of the same functions, previous conversion of the data clinical notation to power vectors (C2V) according to Miller11. In the third column we see the re-conversion of power vectors back to clinical notation (V2C), positive cylinder, and the final column, the negative cylinder clinical notation.

Table 3 Comparison between Index of Ametropia and Power Vectors at ages 3 months 

Table 4 Comparison between Index of Ametropia and Power Vectors at 9 months 

Discussion

Although the proposed Index of Ametropia does not have an optical-anatomical representation, like the Spherical Equivalent or the Defocus Equivalent, it does have the mathematical support of the Principal Meridians of the eye in the same manner that the sides of a right triangle define the hypotenuse.

These methods were already mentioned in the Introductory section, but a short analysis of their shortcomings could be helpful at this point.

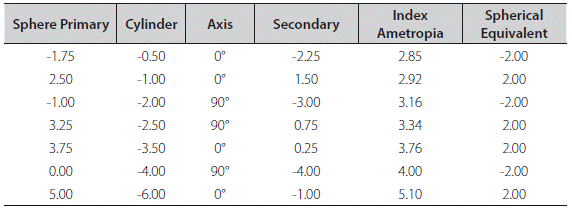
Spherical Equivalent. Its main drawback consists of not differentiating between high and low cylinders which is clinically and statistically inconvenient. Furthermore, a given Spherical Equivalent may represent several refractive states. If we average 6 and 4, the average is 5, the same is obtained with 7 and 3; 8 and 2; 9 and 1 or 4 and 6.

Table 5 illustrates this point with positive and negative ametropias. Column 5 shows the Index of Ametropia of each Ametropia and column 6 shows the corresponding Spherical Equivalent.

Table 5 Comparison between Index of Ametropia and Spherical Equivalent. 

The Indexes of Ametropia are shown in orderly fashion that reflect the increasing severity of the ametropias. The Spherical Equivalent, on the other hand, becomes meaningless reflecting only the plus and minus signs for the corresponding hyperopic and myopic refractions but there is no indication of severity of symptoms that arise in the various states of refraction.

System of Vectors. The axis of astigmatism should not be considered in vector analysis because axes locations do not represent severity in ametropias. Axes at 50° are no more severe than axes at 20°. The proposed Index of Ametropia does not take cylinder axis avoiding unnecessary mathematical calculations.

Categorization of Ametropias. Categories of ametropias are amenable to statistical analyses but only by non-parametric methods. The Index of Ametropia allows any kind of statistical analysis.

Defocus Equivalent. Holladay4 does not specify the mathematical handling of adding the absolute value (+) of the cylinder to the Spherical Equivalent in case of myopia (-) or hyperopia (+). Furthermore, the drawbacks of the Spherical Equivalent apply equally to the Defocus Equivalent. The Index of Ametropia avoids unnecessary calculations and acts solely on the power meridians of the ocular refraction.

Furthermore, the proposed Index of Ametropia excels the current methods of summarizing and handling refractive data for statistical analyses and is based on the following criteria:

As shown in Table 3 and 4, Miller's11 method (based on Long's8 formulae, also used by Harris9 and Thibos10) can produce "average refractions", "median refractions", "mode refractions" and "standard deviation refractions". This is achieved by converting the clinical notation (Sphere, Cylinder and Axis) into separate vectors (M, J0 and J45) and finally convert the vectors back into clinical notation. Mathematically speaking, there is no objection. However, it is not easy to judge or qualify, the results in terms of severity for the simple reason that the index of severity has not been specified. On which component should we base our criterions for appraising the severity of the results: the sphere? the cylinder? the axis?

Tables 3 and 4 correspond to a study to determine the emmetropization evolution of the refractive state in premature newborns at ages 3 and 9 months. First column of the tables shows the Index of Ametropia for mean, median, mode and standard deviation. It is easy to observe at a glance, the refractive changes whereas, the power vector method does not clearly indicate whether the significant refractive changes correspond to the sphere, the cylinder or the axis. Furthermore, a closer look at Tables 3 and Table 4 shows the difference between the media of IA at 3 months (3,15) is much higher than at 9 months (1,90) meaning that ametropia at 3 months is also higher than at 9 months. This corresponds to the well-known emmetropization process14.

We believe that the refractive state should not be broken into sphere, cylinder and axis. It makes it difficult to discern which component reflects more accurately the severity of a refractive state. One may ask, which is more severe, a 4,00 Dpt. Sphere or a 4,00 Dpt. Cylinder. Our Index of Ametropia takes care of refractive states by disregarding the cylinders and axes and taking into consideration the two principal meridians instead.

Another important aspect has to do with visual care epidemiological studies. The proposed Index of Ametropia can be used to calculate all the descriptive statistics needed for such purpose (media, median, mode, standard deviation, variance, correlations, anova, etc.) and the inferential analyses that may be required.

Nevertheless, we must consider a situation in which it is desirable to estimate the Ametropia, spherical or astigmatic, behind a given Index of Ametropia. The Index of Ametropia as it has been conceived, does not lend itself to go backwards to find the ametropia from which it was derived. In other words, given only the hypotenuse, it is not possible to determine the sides that originated it. However, this is not necessarily a disadvantage since in epidemiology, it is the graveness of the sequalae caused by a defective refractive state, that really matters.

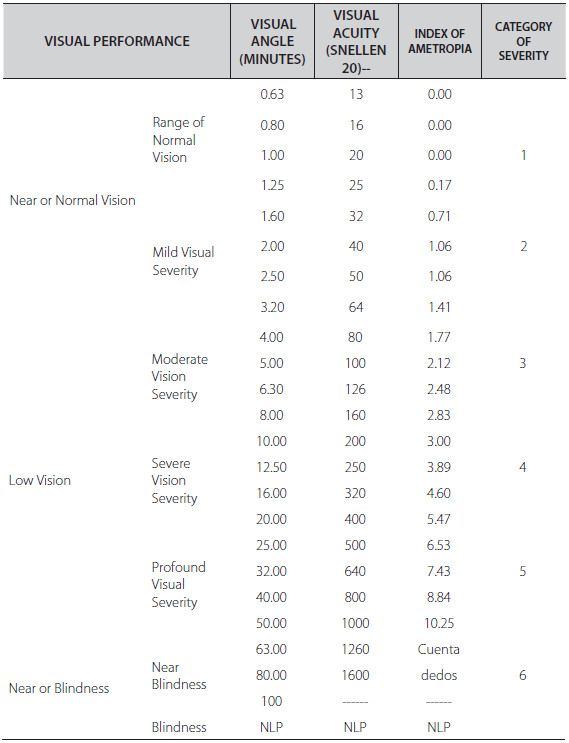
It seems more logical to take the Index of Ametropia to a Severity Scale Table 6, the Index of Ametropia obtained in some epidemiological research, to conclude, possibly, that the group under scrutiny, may require the attention of local or state authorities to correct whatever factor is acting on the population (illumination, nutrition, environment, etc.). In addition, the Index of Ametropia allows the comparative analysis of samples from different populations or, same population at various times.

Summarizing, the Index of Ametropia that encompasses the power meridians of the ocular refraction into a single number, is a valuable tool in epidemiological visual health research facilitating the application of descriptive and analytical statistics.

Table 6 Severity Scale of Index of Ametropia 

Conclusions

Spearman Correlation of 0,834 between Index of Ametropia and M.A.R., is statistically significant (p: < 0,001) and allows us to conclude that the Index of Ametropia is a valid indicator for assessing the severity of both, spherical or astigmatic ametropias and consequently lends itself for proper quantitative and statistical analyses. The r2 obtained, indicates that 62,56 % of variations of M.A.R. are directly related to variations in the Index of Ametropia. The remaining 37,43 % depends on other factors such as accommodation in hyperopes, age, pupil size and general health. In addition, Index of Ametropia and is an adequate tool for categorizing ametropias in accordance to the severity of the visual symptoms and degree of impairment caused thereby.