Introducción
La enseñanza de la física en la educación media, según el currículo colombiano (Ministerio de Educación Nacional, 2006), solo hace referencia a la física clásica dejando fuera las teorías más modernas como la relativista y la cuántica. Se deben cubrir temáticas de la mecánica clásica, temas muy importantes, pero sin referencia a los conceptos de la física actual como probabilidad, comportamiento de electrones, relatividad, entre otros.
Este trabajo forma parte de una tesis doctoral, basada una estructura conceptual propuesta para enseñar el comportamiento de los electrones (Fanaro, 2009). Adaptamos la secuencia didáctica a partir de los obstáculos detectados en implementaciones previas para el contexto de la escuela secundaria colombiana, incorporando nuevas simulaciones para una mejor comprensión al mostrar los valores reales y los resultados en forma gráfica y numérica (Alvarado y Fanaro, 2017).
En la secuencia presentamos el modelo cuántico de considerar caminos alternativos (cca), que es el resultado de la transposición didáctica del enfoque de la integral de camino, dadas las ventajas que ya han sido detalladas en otras investigaciones (Arlego, 2008). El potencial para adaptar las integrales a sumas vectoriales y encontrar la probabilidad para diversos eventos cuánticos las hace potencialmente versátiles a la hora de emplearlas como estrategia didáctica, además permite la conceptualización de la universalidad de las leyes de la mecánica cuántica.
Antecedentes del problema
La necesidad de que el estudiante entre en contacto con saberes básicos de la física de vanguardia, que serán sustento de conceptos más complejos, es reconocida en múltiples investigaciones (Akarsu, 2010; Cid y Dasilva, 2011; Cuesta y Mosquera, 2016; Cuesta, 2018; Fanaro, 2009; Fernández et al., 2005; Frechina, 1996; Gil et al., 1987; Greca, 2000; Greca y Moreira, 2001; Jara-millo, 2015; Johnston et al., 1998; Martínez et al., 2016; Monteiro, 2010; Moreno y Guarín, 2010; Pantoja et al., 2013; Savall, 2015; Sinarcas y Solbes, 2013). En algunas, se presentan secuencias de enseñanza de conceptos cuánticos como parte de la enseñanza de física moderna y contemporánea, pero desde un enfoque canónico o histórico. A diferencia de estas propuestas, hay trabajos realizados desde el enfoque de Feynman para la mecánica cuántica, conocido técnicamente como integral de camino (Feynman y Hibbs, 1965). Este enfoque, alternativo al canónico, comenzó a utilizarse con la propuesta de Taylor et al. (1998), que se basó en el reconocido texto de Feynman (1985) QED: The strange story of light and matter. La integral de camino es en sí misma una herramienta compleja, sin embargo, la esencia del método puede ser comprendida mediante consideraciones geométricas con vectores y operaciones matemáticas, que son accesibles a los estudiantes. Este enfoque resulta apropiado para calcular la probabilidad de ocurrencia de distintos eventos con luz o con electrones, para introducir a los estudiantes en nociones cuánticas fundamentales como probabilidad y superposición. Reconociendo el potencial didáctico que presenta el enfoque de Feynman, varios investigadores lo han adoptado para enseñar aspectos básicos de mecánica cuántica. Así, los trabajos pioneros en esta línea fueron los de Dowrick (1997), Hanc y Tuleja (2005), Dobson et al. (2006) y Ogborn et al. (2006). Malgieri et al. (2014; 2015; 2017) también utilizan este enfoque, incorporando simulaciones realizadas con el software GeoGebra.
La teoría de los campos conceptuales de Vergnaud (1990) postula que el conocimiento está organizado en campos conceptuales, esto es, en conjuntos de situaciones que requieren determinadas operaciones y que el sujeto aborda mediante esquemas afines a cada una de ellas. Para que alguien pueda dominar un determinado campo conceptual, necesita de aprendizaje y experiencia; el campo conceptual cubre un conjunto heterogéneo de problemas, situaciones, conceptos y contenidos cuyo dominio requiere procedimientos y representaciones, es decir, demanda conceptos de diversa naturaleza. Consideramos que el amplio campo conceptual de la mecánica cuántica, posible de ser reconstruido con los estudiantes, queda circunscripto a las situaciones que componen la secuencia didáctica que fue implementada. Lejos de ser una limitación, esto forma parte de nuestra postura didáctica, inspirada en la idea de transposición didáctica de Chevallard (1999); dado que el hecho de diseñar una secuencia para enseñar implica un profundo estudio para transformar el saber y adaptarlo para que tenga sentido para el estudiante.
El constructo de esta teoría es el de concepto. Este permite vincular lo cognitivo y lo didáctico, puesto que se define en función de tres elementos interdependientes: 1) las situaciones que dan sentido y hacen significativo el concepto, 2) los invariantes -conceptos y teoremas en acto usados por el sujeto para analizar y dominar una situación- sobre los cuales reposa la forma operatoria de los esquemas (el significado), y 3) las representaciones simbólicas del concepto y sus propiedades.
El concepto es pragmático y se forma dentro de tipos de situaciones que le dan sentido; en cada situación el sujeto hace uso de invariantes operatorios y de representaciones que le permiten referirse al concepto. De ahí la importancia de la selección o diseño de las situaciones que serán los contextos propicios para hacer emerger los conceptos cuánticos. Por su parte, los invariantes operatorios tienen la función de reconocer e identificar los objetos, sus relaciones, sus propiedades y sus transformaciones. En esto consiste la función de conceptualización y de inferencia. Un teorema en acto es definido en esta teoría como una proposición tenida como verdadera por el sujeto en medio de la actividad. Un mismo concepto en acto puede asociarse a numerosos teoremas diferentes, más o menos complejos y no necesariamente verdaderos (o sea no científicamente aceptados). En este trabajo solamente nos enfocamos en los teoremas en acto que pudieron haber guiado la conceptualización, los cuales nos permitirán entender los posibles obstáculos y las ayudas a la conceptualización que la secuencia pudo haber hecho emerger en los estudiantes. A su vez, este conocimiento nos da indicios de la viabilidad de la propuesta, así como de la distancia entre la conceptualización pretendida y la realmente realizada por los estudiantes.
La secuencia de situaciones propuesta
Las primeras dos situaciones proponen analizar los resultados de la experiencia de la doble rendija (edr) con el objetivo de establecer el comportamiento característico de los electrones y diferenciarlo del de las partículas de mayor masa. Se solicita imaginar la experiencia utilizando primero canicas como proyectiles y luego electrones. Después se pide simular la experiencia con el software Doppelspalt para ofrecer a los estudiantes la posibilidad de corroborar o contrastar sus respuestas con los resultados.
En la tercera situación se plantea la cuestión sobre cuál modelo permite dar cuenta de la distribución de los electrones, pero se propone una situación más elemental antes: el cálculo de la probabilidad de detectar una partícula que en cierto tiempo se encuentra en un lugar considerado inicial (i) y luego en otro (f); después se indica volver al caso de la edr. Este cálculo de probabilidad se conoce en la literatura científica como la suma de caminos alternativos de Feynman, pero con los estudiantes se denomina técnica de considerar los caminos alternativos (cca) (Fanaro et al., 2012). El análisis de representaciones gráficas y operaciones básicas con vectores es esencial en este enfoque porque allí se concentran los aspectos esenciales de la teoría cuántica: el principio de superposición y la validez universal de esta teoría.
Como parte fundamental de la transposición didáctica realizada, el diseño de la secuencia incluye el trabajo con plantillas de cálculo elaboradas por el equipo de investigación para los estudiantes. Se muestra un gráfico en coordenadas cartesianas (x-y) y se permite el ingreso de distintos puntos que hacen variar los caminos que conectan el inicio (i) con el final (f). El objetivo de dichas plantillas es simular los resultados del cálculo y visualizar la suma de los vectores gráficamente, puesto que esta suma es un indicador de la probabilidad de detección. Las figuras 1 y 2 representan las plantillas de cálculo del evento libre con electrones para caminos cercanos y lejanos al camino directo, respectivamente.

Fuente: elaboración propia.
Figura 1 Evento libre con electrones para veinte vectores asociados a caminos cercanos al camino directo y el camino directo, valores de las variables Angulo y Acción, y vector unitario asociado a cada camino con su aporte a la suma de todos los vectores

Fuente: elaboración propia.
Figura 2 Evento libre con electrones para veinte vectores asociados a caminos lejanos al camino directo
Las primeras tareas se dirigen a analizar los valores de acción (s) mostrados en la plantilla, y se propone a los estudiantes variar las condiciones de los puntos de detección inicial y final que generan diferentes "caminos" para conectarlos. Se pretende consensuar que para los caminos cercanos al camino directo el ángulo es muy parecido al ángulo del camino directo, y en todos los casos, la acción es mínima en el punto de detección correspondiente con el camino directo.
En esta adaptación de la técnica no se calcula la probabilidad directamente, puesto que es proporcional al cuadrado del módulo del vector resultante en la suma, valor llamado con los estudiantes frecuencia de ocurrencia relativa (fr), que es calculado y mostrado en la plantilla de cálculo. Correlativo al análisis previo con la suma, se institucionaliza con los estudiantes que los puntos de detección correspondientes al camino directo y los que están a su alrededor tienen mayor probabilidad de detectar electrones que en puntos de detección correspondiente a caminos alejados del camino directo. Para presentar una situación donde los estudiantes puedan poner en juego la idea de la contribución del camino más directo y los de su alrededor, propusimos al final de esta situación el cálculo de la fr en el caso de un "billar cuántico", donde se manifiesta un "evento rebote", como se muestra en la figura 3. Allí se analiza la probabilidad de detección de electrones en distintos puntos para concluir que el punto donde será más probable detectar un electrón que habiendo salido de una esquina realice un "rebote" y llegue a la tronera opuesta es el punto medio del lado donde se produce el rebote correspondiente con el camino directo y los caminos cercanos a él.

Fuente: elaboración propia.
Figura 3 Imagen de la plantilla de cálculo del evento rebote con electrones para veinte vectores asociados a caminos cercanos al camino directo y el camino directo, en el cual se observan los valores de las variables Angulo y Acción, así como un vector unitario asociado a cada camino y el aporte a la suma de todos los vectores
La cuarta situación propone aplicar la técnica CCA para partículas de masa mucho mayor que la del electrón (como canicas) y analizar la probabilidad en los mismos eventos con electrones.
La quinta situación reconstruye el diagrama en la pantalla de la simulación con el software Doppelspalt y busca dar cuenta de la forma de la curva de probabilidad P(x), al encontrar un modelo matemático que la represente. Se presenta a los estudiantes la formulación algebraica de la suma de los vectores para el caso de la edr, aplicando la idea construida en la situación 3: los únicos vectores que contribuyen a la suma son los correspondientes al camino directo y sus alrededores; y al tratarse de dos rendijas, se tiene entonces la suma de los dos vectores principales. De la sucesión de pasos algebraicos, se obtiene una función coseno cuadrado. Esto permite interpretar la curva antes obtenida en términos de lugares donde será posible encontrar electrones en zonas de máximos y mínimos. La última tarea de esta situación es inversa a las anteriores: se ofrece a los estudiantes varios esquemas donde se muestra la gráfica de P(x) yuxtapuesta al esquema de la EDR para que reconstruyan la suma de los dos vectores principales (véasefigura 4).
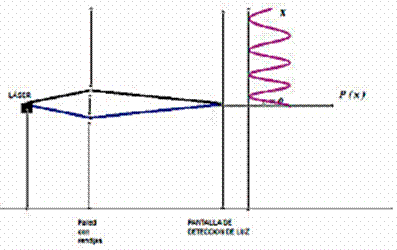
Fuente: adaptado de Fanaro y Elgue (2018, p. 279).
Figura 4 Ejemplo de esquema presentado a los estudiantes en la última parte de la situación 5
Esta tarea presenta un alto grado de complejidad pues implica relacionar los tres sistemas de representación asociados al cálculo de la probabilidad: los vectores asociados y su suma, la configuración de la experiencia en el esquema plano, y la función de probabilidad indicando las zonas de gran presencia o ausencia de electrones.
La sexta, y última, situación propone el estudio de la transición cuántica-clásica a partir de la aplicación de la técnica cca tanto a partículas cuánticas como clásicas.
Metodología
Esta investigación es exploratoria, descriptiva e interpretativa; analiza la conceptualización que se produce cuando los estudiantes afrontan las tareas que se proponen en cada situación de la secuencia didáctica. Esta se implementó en cuatro cursos de física en un colegio público perteneciente a la Secretaría de Educación de Bogotá, durante el tercer trimestre de los años 2016 y 2017, dos grupos por año, con n = 118 estudiantes en total. Corroboramos la homogeneidad de los estudiantes de los cuatro cursos realizando una prueba de comparación en medias de sus desempeños en el curso de Física previa a la implementación.
En las implementaciones, el investigador adoptó el rol de profesor, con una metodología de trabajo en aula que privilegia la acción de los estudiantes, quienes en grupo leían, interpretaban, interactuaban con el docente para realizar las consultas necesarias y desarrollaban las tareas propuestas.
Una vez finalizada la implementación, se digitalizaron las resoluciones de los estudiantes y, a partir de ellas, se realizó una categorización inductiva de las respuestas para interpretar los resultados a la luz de la teoría de los campos conceptuales. Entendemos las acciones requeridas para la conceptualización buscada como las variables, y como modalidades de estas, los teoremas en acto identificados en las resoluciones de los estudiantes a una o varias situaciones. Es decir, el análisis no se realizó por situación, sino por los teoremas en acto que logramos identificar en las distintas fases de la conceptualización. Consideramos que esas proposiciones tenidas como verdaderas por los estudiantes son las que estarían subyaciendo y guiando cada tipo de resolución, inferimos los teoremas en acto que representaría el tipo de resolución y los ordenamos en un gradiente hacia la mejor conceptualización lograda por los estudiantes. La tabla 1 presenta un resumen de la categorización.
Tabla 1 Las seis fases de conceptualización, las tareas propuestas para el desarrollo de cada una de ellas entendidas como acciones para la conceptualización y teoremas en acto de los estudiantes en gradiente de conceptualización

Fuente: elaboración propia.
Luego de realizar un análisis univariado para tener un panorama de cómo se distribuyeron las respuestas de los estudiantes según las categorías formuladas y del análisis bivariado para encontrar si había categorías dependientes de a pares, se realizó un análisis factorial de correspondencias múltiples (AFCM) (Benzécri, 1980; Lebart et al., 1985; López-Roldán y Fachelli, 2015) con el paquete estadístico SPAD®, versión 8.1, para analizar la asociación o interrelación entre más de dos variables en simultáneo.
Utilizamos la técnica de análisis de correspondencias múltiples (acm) (Benzécri, 1980; Lebart et al., 1985), dada la naturaleza categórica ordinal de los datos obtenidos. Se hizo una reducción de los datos al identificar los factores que sintetizan las variables de este estudio, para lo cual se tomaron solamente las categorías correspondientes a las fases de la 3 a la 6, dado que las primeras dos se consideraron de predicción.
Resultados y análisis
En la figura 5 se presenta el plano factorial, confeccionado a partir de las contribuciones de las variables involucradas. Este es una representación gráfica sintética en el que se utilizan las primeras coordenadas factoriales para presentar la información inicial, las variables y sus modalidades (cuadrados rojos). En esta misma imagen, se muestra las clases de individuos con similitudes al respecto de ese conjunto de variables y sus modalidades (círculos amarillos), como analizaremos a continuación.

Fuente: elaboración propia.
Figura 5 Plano factorial del análisis de correspondencias múltiples, cuyos ejes son el Factor 1 (eje horizontal) y el Factor 3 (eje vertical), por contribución
A partir del AFCM y el plano factorial (véasefigura 5), es posible visualizar las principales asociaciones y oposiciones entre las modalidades de las variables cualitativas utilizadas, analizando las distancias que se representan en el plano.
Los tres primeros factores acumulan el 89,68 % de la varianza explicada. Los factores 2 y 3 explican aproximadamente la misma varianza (16,80 % y 15,86 %, respectivamente). Se decidió analizar el plano factorial conformado por el Factor 1 y el Factor 3, porque permiten una interpretación más satisfactoria de los datos (Moscoloni, 2011). Así, entre el Factor 1 y el Factor 3 se acumula casi el 73,0 % de la varianza total. La tabla 2 muestra las categorías y subcategorías que conforman cada uno de los ejes.
Tabla 2 Conformación de los factores 1 y 3
| Factor 1. Eje abscisas | Factor 3. Eje ordenadas | ||
|---|---|---|---|
| Categoría de Modalidad de la | Categoría de | Modalidad de la | |
| análisis | variable | análisis | variable |
| PCL | PCL1 | CAC | CAC2 |
| IPC | IPC1 | IFP | IFP2 |
| PCR | PCR1 | PCR | PCR1 |
| CEP | CEP1 | PER | PER1 |
| STC | STC2 | IPS | IPS1 |
| CAC | CAC1 | PER | PER3 |
| IFP | IFP1 | CEP | CEP1 |
| PEL | PEL1 | PCL | PCL3 |
| Opuestas a: | Opuestas a: | ||
| CAC | CAC3 | IPS | IPS2 |
| PCL | PCL3 | CAC | CAC3 |
| STC | STC3 | PCL | PCL2 |
| CEP | CEP2 | ATC | ATC3 |
| ATC | ATC3 | STC | STC2 |
| PCL | PCL2 | IFP | IFP1 |
| PCR | PCR3 | PEL | PEL1 |
| IPC | IPC3 | PER | PER2 |
Fuente: elaboración propia.
El Factor 1 en el eje de las abscisas representa el 57,02 % de la varianza explicada. Indica que las mayores diferencias relativas en la conceptualización se relacionan con el cálculo de la probabilidad para canicas y su interpretación cca, que son situaciones relativas al uso de la simulación del modelo planteado con la planilla Excel. Las mayores diferencias se relacionan con la identificación y explicitación de las diferencias entre la EDR mostrada por el software y la interpretación de la función de probabilidad para el caso de las canicas. En este factor, el semieje negativo agrupa los teoremas en acto que representan la con-ceptualización más baja del análisis de la técnica y el cálculo de la probabilidad para canicas. Estos teoremas en acto presentan sus opuestos en términos de conceptualización en la zona, con lo cual interpretamos que el semieje positivo o eje de abscisas que representa al Factor 1 agrupa aquellos teoremas en acto referidos a una conceptualización más bien rica acerca de la interpretación de la técnica de considerar los caminos, y luego poder aplicarla al cálculo e interpretación de la probabilidad en las experiencias que involucran canicas.
El primer eje factorial separa, en el extremo derecho, las categorías que describen las construcciones de los estudiantes con un alto nivel de conceptualización en el análisis del comportamiento de partículas clásicas, de las categorías que describen construcciones de bajo nivel de conceptualización, ubicadas en el extremo izquierdo. Este último caso reúne a aquellos estudiantes que desde el inicio expresaron que la acción es un valor numérico cambiante simplemente. Este grupo no mencionó el hecho de que la acción tiene un valor asociado a cada grupo de caminos y menos aún que para ciertos grupos de caminos su valor era menor comparado con otro tipo de caminos, situación que no les permitió luego enfrentar correctamente la construcción de la probabilidad para los eventos con canicas. Este eje podría denominarse Uso de la técnica cca con electrones y su extensión a canicas.
El Factor 3, eje de las ordenadas, representa las situaciones relativas a los electrones cuando se aborda la técnica por primera vez y cuando se aplica en la EDR, es decir la modelización que ofrece la cca y la contrastación empírica en la EDR con electrones. Este eje podría denominarse Uso de la técnica cca con electrones y su aplicación a la EDR. En el semieje positivo se representan aquellos teoremas en acto que, si bien no son los mejores para la conceptualización del comportamiento del electrón, en el sentido de estar incompletos, se encuentran "a mitad de camino" hacia la conceptualización buscada. En este semieje, se representan los teoremas en acto relacionados con que la acción cambia y siempre lo hace para aumentar a partir de un valor mínimo que es el de mínima acción correspondiente con la acción del camino directo. Cuando se analiza la contribución de los caminos, se acepta que el grupo de caminos cercanos al camino directo y el camino directo son los más probables para el caso de los electrones, y se encuentra que los resultados que presentan las fotografías se relacionan con la gráfica de la P(x), en una comprensión bastante acertada aunque incompleta acerca de la modelización.
En cambio, en el semieje negativo se representan aquellos teoremas en acto que indican problemas en la conceptualización. En cuanto a la técnica cca, se conceptualiza que la acción es una cantidad que puede variar según el camino que sigue el electrón, sin discriminar su cambio para cada grupo de caminos; no se caracteriza su valor para el camino directo y los caminos cercanos al camino directo. En cuanto a la probabilidad del electrón con efecto rebote, se obtiene únicamente la cantidad numérica, lo cual da a entender que no fue interpretada por esta parte de los estudiantes, es decir que la mo-delización no fue percibida como tal por ellos.
Resulta interesante reunir a los individuos de acuerdo con su similitud; para formar grupos de individuos a partir de estas características relacionadas. En este caso se seleccionó una partición en tres clases. Según se aprecia en el gráfico de la figura 5, cada grupo está representado por círculos amarillos.
El clúster 1/3 agrupa a aproximadamente la mitad de los estudiantes (51,69 %), caracterizados por una conceptualización muy pobre acerca de la técnica de cálculo de probabilidad mediante la técnica cca, y de los resultados de la modelización obtenida y su contrastación con la experiencia. Las modalidades que caracterizan a este indican que los estudiantes no alcanzaron a percibir la importancia de la acción mínima, ni el aporte de los caminos vecinos del camino clásico, ni de la cancelación de los caminos alejados. Por lo tanto, sus conclusiones acerca de las probabilidades de detección con canicas libres o con efecto rebote no fueron buenas. Sin embargo, al final de la secuencia, ellos identificaron que el cambio de masa entre electrones y canicas es lo que produce que queden distribuidos de diferente manera en la pantalla (ips3). Podríamos decir que este grupo se caracteriza por tener una baja conceptualización en la técnica cca y en su aplicación a canicas.
El clúster 2/3 es muy pequeño: agrupa a un 4,24 % de los estudiantes. Las modalidades que caracterizan a este grupo indican estudiantes que tienen una conceptualización entre baja y media en cuanto a la técnica, pero bastante baja cuando se trata de aplicarla a la EDR con electrones.
El clúster 3/3 reúne a 52 estudiantes (44,07 %). Este grupo fue el que mejor conceptualizó la técnica cca, al comparar las acciones y los caminos; también evaluó los aportes de los vectores de los caminos asociados al emplear la técnica con electrones y logró un análisis satisfactorio de la probabilidad de canicas tanto libres, como con efecto rebote, aceptando así que la función de probabilidad que se obtiene con la cca de Feynman es un modelo que representa los resultados obtenidos en la EDR. También los estudiantes hicieron una buena interpretación de la función de probabilidad y EDR con canicas.
Conclusiones
Según los resultados, más de la mitad de los estudiantes lograron superar los obstáculos y alcanzaron desarrollos aceptables en la conceptualización, es decir que los tiempos y las actividades previstas resultaron suficientes para este grupo. Sin embargo, esto invita a reflexionar acerca de la incidencia en los obstáculos iniciales en la conceptualización, lo cual constituye un desafío para nuevos desarrollos didácticos. En lo que respecta a la secuencia, se propone que esta tenga tareas complementarias que permitan superar los obstáculos en la conceptualización previa para que al estar frente a las situaciones posteriores, estas puedan ser superadas. También se sugiere plantear tareas intermedias en aspectos como el conocimiento y la manipulación de la técnica CCA, así como el análisis y cálculo de la probabilidad para electrones y canicas.
Por último, es preciso señalar la influencia de la familiaridad del profesor con la secuencia didáctica en la conceptualización alcanzada por sus estudiantes, pues el clúster 1/3 corresponde a las resoluciones del año 2016, mientras que el clúster 3/3 agrupa las resoluciones del año 2017. Además, estos grupos fueron considerados homogéneos según el análisis de comparación en medias de sus calificaciones antes de comenzar la implementación. Esto da indicios de que al ser la secuencia didáctica un producto diseñado por expertos en didáctica y en física, resulta ser que la familiaridad y el dominio de la secuencia que el docente presentó luego del primer año le permitieron tener más elementos en la actividad académica adentro del aula en la siguiente implementación.















