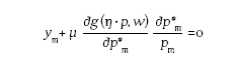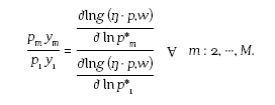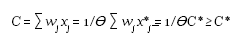1. Introduction

During and immediately after the 2007-2009 U.S. financial crisis, 322 U.S. commercial banks failed. The estimated loss for the Federal Deposit Insurance Corporation (FDIC) was $86 billion. Both the number of bank failures and their associated cost increased tenfold compared to the years between 2000 and 2007. From 1980 to 1989, 1,467 U.S. commercial banks failed (estimated cost $62 billion) and from 1990 to 1999 this number was 436 (estimated cost $7 billion)¹. Despite the severity of the recent crisis, the number of bank failures was low compared to previous crisis episodes. The natural question arising from these facts is what was different this time around.

In the U.S. the FDIC manages bank failures and is usually appointed as a receiver for failing banks. The narratives presented in the Material Loss and In-Depth Reviews (MLIR) conducted by the FDIC Office of Inspector General indicate that a bank fails mainly because the bank has: 1) inadequate corporate governance; 2) weak risk management; 3) lack of risk diversification/lending concentration; 4) deteriorating financial conditions; and 5) insufficient capital to continue sound operations². The risk management manual of examination policies of the FDIC (the FDIC closure guidelines, henceforth), includes six factors to assess the soundness of supervised banks: capital adequacy, asset quality, managerial practices, earnings quality, liquidity position, and sensitivity to market risk. These six factors are commonly known by the acronym CAMELS. By construction, the proxies for CAMELS factors have high explanatory power regarding the probability of bank failures in the U.S. since the FDIC recommends bank closures or prompt corrective actions based on them. Not surprisingly, a robust finding in the academic literature is that CAMELS components constitute the main factors influencing the probability that a bank fails (e.g. ^{Cole and Gunther 1995}; ^{Wheelock and Wilson 2000}; Cole and White 2012).

According to the FDIC, "the quality of management is probably the single most important element in the successful operation of a bank" (FDIC guidelines, 2005, p. 4.1.1). However, out of the six CAMELS factors, the managerial component is usually overlooked in the literature since the assessment of managerial practices is not readily amenable to econometric or statistical analysis, in part, because the definition of managerial practices is broad and vague.

In economics, efficiency is defined broadly as the ratio between outputs and inputs. It describes a relationship between ends and means and is measured by comparing their relative values, ^{Heyne (2008}). Consistent with this definition, managerial efficiency can be defined as the ability to achieve the firm's objectives (ends) using the minimum level of resources (means). Ideally, it can be measured by comparing the value of resources used with the value of the outputs produced. However, in applied work this is a difficult task. ^{Bates and Sykes (1962}) argue that managerial efficiency necessarily should be reflected in the profitability of firms: more managerial-efficient firms should be more profitable. ^{Jovanovic (1982)} states that in a market economy profits represent the reward for greater managerial efficiency. Following Bates and Sykes and Jovanovic, we measure managerial efficiency using profit efficiency as a proxy. Profit efficiency is a financial performance measure of the distance between actual profit and the best practice frontier. It captures how efficiently a bank can extract profits from the resources deployed in its operations (see ^{Berger and Mester 1997}; ^{Kumbhakar and Lovell 2003}; ^{Akhigbe and McNulty 2003}, 2005)³3.

To our knowledge, there are only two directly related papers to our work (^{Wheelock and Wilson 2000} and ^{Berger, Imbierowicz and Rauch 2016}). Wheelock and Wilson argue that management quality is difficult to measure directly since it can take several forms. They favor the use of cost and technical efficiency measures as proxies for managerial quality⁴. They find that both proxies are statistically and economically significant predictors of bank failures in the U.S. Most recently, Berger et al. tackles the difficult issue of establishing if a banks' corporate governance system is an important predictor of bank failures in the U.S. They investigate the impact of bank ownership and management structures on the probability of bank failure. They find that a bank's ownership structure strongly influences the probability of bank failures.

We contribute to the financial literature on bank failure and complement the existing studies by showing that profit efficiency, our proxy for the quality of banks' managerial practices, strongly influences the probability that a bank survives the U.S. Financial Crisis of 2007-2009 . We find that profit inefficiency-arguably the most important measure of managerial inefficiency-is a robust predictor of bank failures⁵. ^{Wheelock and Wilson (2000}) present empirical evidence indicating that cost efficiency positively influenced the survival probability of U.S. commercial banks. Our findings indicate that cost efficiency played no direct role on the survival probability of banks during the last financial crisis. In contrast to ^{Moore and Seamans (2013}) and traditional wisdom, our estimates show that the capital adequacy of banks is not a robust predictor of banks' survival during the last crisis. However, loan quality and bank profitability remain strong predictors. Our results suggest that banks' regulators should focus on loan quality and loan mix in monitoring the soundness of banks and that banks' profit efficiency can be an important managerial indicator in monitoring banks.

We use standard hazard regression models to estimate the conditional probability of bank failures. Namely, we show how efficiency and traditional proxies for bank failure affect this probability. Unlike the standard classification models (Logit or Probit), hazard models account for incompletely-observed lifespans of banks surviving past the sample period. Post-crisis studies exclusively use Logit models to model bank failures (e.g. ^{DeYoung and Torna 2013}, ^{Cole and White 2012}, ^{Berger et al. 2016}). Our results offer a robustness check to their results.

Our main hypothesis is that after accounting for traditional factors influencing bank failure, managerial efficiency-as captured by profit efficiency-should be negatively correlated with banks' failure probability as relatively more profit-efficient banks should be less likely to fail, ^{Amel and Prager (2013}). We find that banks' profit efficiency has independent explanatory power and negatively influences the probability of bank failures: the higher the profit efficiency of a bank, the lower its probability of failure. In contrast to previous studies (e.g., ^{Wheelock and Wilson, 2000}), we find that cost efficiency measures are unrelated to bank failures. The results are robust to the inclusion of different sets of control variables and the use of different model specifications. As in Wheelock and Wilson (2000), we find that less diversified banks, as measured by loan-to-asset ratios, are more likely to fail. Thus, recent regulatory measures intended to limit banks' ability to carry out non-traditional activities may actually increase the likelihood of bank failures. In addition, the ratio of real estate and commercial loans to total loans is positively related to bank failures. Banks with low-quality loans, as measured by non-performing loans and loan loss provisions, are also more likely to fail.

An interesting result is that banks that rely on deposits as a major source of loan funding have a higher probability of failure. This result may indicate that deposit insurance leads banks to take on more risk, an explanation consistent with ^{Wheelock and Wilson (1995}) and ^{Demirguc-Kunt and Detragiache (2002}). Further, after accounting for the above factors and earnings quality (measured using returns on assets or return on equity), we show that leverage, asset size, and off-balance sheet activities are unrelated to bank failures. This latter finding may imply that off-balance sheet activities help banks to diversify their portfolio and do not increase their risk of failure.

The paper is structured as follows: Section 2 reviews the literature; Section 3 presents the basic model and variables and describes the data; Section 4 reports the empirical results; Section 5 concludes.

2. Literature Review

The recent U.S. financial crisis of 2008-2009 spurred research on the determinants of the failures of systemically-important banks-systemic banks. This new research focuses on the interconnectedness of modern banking systems and its effects on bank stability and the interconnection with key factors like regulatory framework, monetary policy, bank leverage, capital requirements, bank size, shared risk exposure, liquidity, and funding sources, among others. (^{Glasserman and Young 2016}, ^{Brunnermeier and Sannikov 2014}, ^{Gorton and Metrick 2012}, ^{Lo 2012}, ^{Tirole 2011}, Brunnermeier 2009, ^{Hoshi 2011}). As a consequence, our understanding of such matters as systemic risk, financial instability, and monetary and regulatory policy regimes improved in recent years. However, the causes and determinants of nonsystemic bank failures stemming from the crisis are not yet well understood (^{DeYoung and Torna 2013}, ^{Cole and White 2012}). In this section, we review the post-crisis literature on why U.S. commercial banks failed during the crisis and compare its main results to the pre-crisis evidence.

Given that the U.S. financial crisis was triggered by a mortgage default crisis and the subsequent bad performance of mortgage-backed securities (^{Adelino, Schoar and Severino 2016}, ^{Demyanyk and Van Hemert 2011}, ^{Mian and Suf i 2009}), the post-crisis literature focuses on three main topics:

i) the relation between bank failures and their exposure to the real estate market-in particular, to subprime and non-household borrowers (^{Antoniades 2015}, ^{Cole and White 2012}); ii) the role played by nontraditional banking activities; and iii) the relation of bank failures to bank characteristics-as measured by CAMELS factors-and economic fundamentals.

One of the first papers investigating why U.S. commercial banks failed during the crisis is ^{Cole and White (2012}). They investigate the ability of CAMELS components and measures of banks' real estate investment to predict bank failures during the crisis. They find that after accounting for CAMELS components, banks' exposure to residential mortgage-based securities (RMBS) has no explanatory power in predicting non-systemic bank failures. Higher levels of capital, better asset quality, higher earnings, and more liquidity make banks less likely to fail. However, the exposure to the real estate market in general was associated with a higher probability of failure. These results are broadly consistent with those in ^{Oliveira, Martins and Brandao (2015}) and ^{Li (2013}).

The results in ^{Cole and White (2012}) support the main finding of the pre-crisis literature: CAMELS components are robust predictors of bank failures (^{Whalen 1991}, ^{Cole and Gunther 1995}, ^{Wheelock and Wilson 2000}, ^{Kolari, Glennon, Shin and Caputo 2002}, ^{Estrella, Park and Peristiani 2000}, ^{DeYoung 2003}). In a related paper, ^{Shaffer (2012}) investigate the relative importance of CAMELS components in determining bank-failure probabilities during the crisis and compare these differences to the pre-crisis literature. They find that the risk of bank failure was more sensitive to non-performing loans and banks' profitability in 2008 than in the 1980s. The effect of leverage and capital adequacy seems to have diminished over time.

Non-traditional banking activities like securities brokerage, insurance sales, venture capital, investment banking and securitization figured prominently as contributing factors to the U.S. financial crisis. ^{DeYoung and Torna (2013}) investigate the role of such activities in predicting bank failures during and in the aftermath of the crisis. They find that pure-fee based non-traditional activities (e.g., securities brokerages and insurance sales) reduce the probability of bank failures. Asset-based non-traditional activities (e.g., venture capital, investment banking, and securitization) increase it. DeYoung and Torna show that banks' risk-taking through non-traditional activities is associated with greater risk-taking in their traditional lines of business. Their results suggest that managerial decisions play an important role in determining the riskiness of banks' activities and that other soft factors (e.g., bank ownership, management efficiency, and corporate governance in general) may play an important role in influencing bank failures.

Other researchers investigate how local economic conditions relate to the survival and failure of banks. According to ^{Cebula (2010}), non-systemic bank failures between 1970 and 2007 were linked to fundamental economic factors (e.g. unemployment rate, bank's funding costs, stock market uncertainty, regulatory changes, and loan quality). ^{Aubuchon and Wheelock (2010}) show that most bank failures in the 1980s and early 1990s occurred in U.S. regions experiencing unusual economic distress. Regulatory constraints seem to have played an important role as banks were unable to geographically diversify their risk. ^{Aubuchon and Wheelock (2010)} investigate the role of local economic conditions in bank failures during the U.S. financial crisis. They find that bank failure rates were higher in states with severely-deteriorated economic conditions. Thus, in spite of the lifting of most intra-states regulatory constraints between 1995 and 2005, local economic conditions still played an important role in determining the survival probability of banks.

Other studies investigate the role of individual CAMELS components on the probability of bank failures. ^{Hambusch and Shaffer (2016}), for instance, propose an early warning model using bank leverage as the main determinant of bank failures. They show that their model performs well in predicting bank failure in normal times but not during economic downturns or crisis episodes, highlighting the limitations inherent in focusing on only some CAMELS components to predict bank failures.

^{Bologna (2015}) investigate the role of funding structure and funding mix in predicting bank failures during the crisis (2008-2009). They use the loan-to-deposit ratio as a proxy for banks' funding structure. Consistent with empirical and theoretical arguments regarding the superiority of deposit funding over non-deposit funding, they find that bank failures are positively related to banks' reliance on non-deposit funding and that the larger the share of non-deposit funding, the higher the probability of failure. These results are similar to those reported by ^{Schaeck (2008}) and ^{Miller, Olson and Yeager (2015}).

None of the above-mentioned studies deal with the issue of how managerial efficiency affects the probability of a bank failure, which is the focus of the present paper. The literature regarding these effects is scant and by now dated. The seminal paper in this line of research is ^{Wheelock and Wilson (2000}). Using data from 1984 to 1993 and after controlling for traditional CAMELS factors, they find that managerial efficiency, as measured by cost and technical efficiency, was a robust predictor of bank survival probabilities. More recently, ^{Berger et al. (2016}) shed some light on why low managerial efficiency may be associated with lower rates of bank survival. It turns out that bank ownership, and in particular, the stakes in the banks, determines the risk-taking of lower-level management and, ultimately, bank failures. They present evidence that bank failure probabilities increase when chief officers and lower-level management incentives are aligned in this way.

In a related managerial paper, ^{Gilbert, Meyer and Fuchs (2013}) investigate what distinguishes thriving U.S. community banks. They define thriving banks as those that were able to maintain a high supervisory rating during the crisis (2006 to 2011). Supervisory ratings capture the overall performance of banks with respect to the CAMELS components. In addition to hard information (e.g. financial ratios), supervisory ratings also include soft information regarding banks' managerial quality. ^{Gilbert et al. (2013)} analyze the differences between the thriving banks and the "surviving banks"-i.e., those that did not fail but maintained a low supervisory rating. They interviewed the leaders of a sample of thriving banks to investigate how they were able to outperform their peers during the crisis. They find that managers of thriving banks maintained a strong commitment to conservative lending practices. However, thriving banks follow different business plans to achieve their objectives. No single model seems to be able to capture the diversity of these banks' business strategies or explain their success.

3. Methodology

In our analysis we estimate the time-to-failure probability of U.S. commercial banks using standard hazard model regressions. We focus on testing if managerial efficiency measures commonly used in the literature (e.g., profit, cost, and revenue efficiency) have independent explanatory power to predict bank failures. To measure managerial efficiency we favor the use of a profit efficiency measure over cost or revenue efficiency measures taken in isolation. In this section, we explain the econometric methods used to estimate managerial efficiency and time-to-failure probabilities.

We follow ^{Wheelock and Wilson (2000}) in modeling the time-to-failure of U.S. banks. We use ^{Cox (1972)} proportional-hazard models with time-varying covariates⁶.We favor the use of hazard models overstatic classification models (e.g. Probitand Logitmodels) for several reasons. First, hazard models can control for the time a bank is at risk of failure. Static models give biased and inconsistent probabilities of failure given that they ignore that banks change over time. Second, hazard models incorporate the panel structure of the data and accommodate bank-specific and industry or macroeconomic covariates. Third, hazard models outperform static models in out-of-sample forecasting (See ^{Shumway 2001}, ^{Cole and Wu 2009}, and ^{Demyanyk and Hasan 2010} for details)⁷.

We use four measures to proxy for bank managerial efficiency. We estimate profit and revenue efficiencies using the non-standard profit function framework of ^{Humphrey and Pulley (1997}) and estimate cost efficiency using a cost function, which is standard in the literature⁸. We also estimatea composite profit efficiency measure following ^{Restrepo-Tobon and Kumhakar (2011}). This measure is a profit efficiency measure that captures both revenue and cost efficiency. It differs from the traditional profit efficiency measure in that it is computed from separate measures of revenue and cost efficiencies rather than from a profit function. Previous studies focus on cost and technical efficiency. For instance, ^{Wheelock and Wilson (2000}) use three measures of efficiency: cost efficiency, input-oriented technical efficiency, and output-oriented technical efficiency⁹. We believe that profit efficiency provides a superior measure of efficiency over these measures since it encompasses all of them in a single measure.

We follow ^{Humphrey and Pulley (1997}) and assume that banks maximize profits, П = R − C =∑m pmym − ∑ j wj xj , subject to technological and market constraints, where pm , m = 1, • • • , M are the prices for the corresponding vector of output quantities y and wj , j = 1, • • • , J are the input prices for the corresponding vector of input quantities xj . We model the bank' technology using the transformation function, A f (y, Ɵ • x) = 1. The market constraints are modeled using the price possibility frontier (PPF), g (ŋ • p, w, z) = 1, where z capture any bank characteristic that influences its pricing strategies other than prices and outputs. g (•) captures the ability of banks to set output prices for given input prices conditional on banks technology. It is analogous to the transformation function. It is natural to think that banks take into account input prices in setting prices. However, their ability to charge differential prices will depend on bank technology, therefore, the g (•) function should share some properties with the transformation function. It can be thought as the banks' assessment of appropriate output prices given its technology and exogenously given input prices. Technically, it plays a similar role to the demand function in the classical monopoly model. Technical inefficiency (input-oriented) in the transformation function is introduced via 0≤Ɵ≤ 1. Similarly, price inefficiency (measured radially like technical inefficiency) shows the rate at which banks could increase their output prices (represented by ŋ ≥ 1) given market conditions¹⁰. The PPF could includeother exogenous variables that could potentially affect banks' pricing policies.

Note that unlike in ^{Berger, Humphrey and Pulley (1996}) and ^{Humphrey and Pulley (1997)}, ^{Restrepo Tobon and Kumhakar (2011)} explicitly introduce price inefficiency (η ≥ 1) into the PPF. This allows the PPF to dispense with output quantities. In this case, the relation between input prices and output quantities, in the spirit of Berger et al. and Humphrey and Pulley, results naturally from the first order conditions of the profit maximization problem. We present details of the derivation of the profit, revenue, and cost efficiency measures in the Appendix.

We assume a flexible (translog) functional form for modelling the non-standard profit function, П (w, y), the non-standard revenue function R (w, y), and the standard cost function C (w, y). The translog function is widely used in the stochastic frontier literature, ^{Kumbhakar and Lovell (2003})¹¹.

The econometric specification is:

()1

In equation 1, Q represents either total profits, total revenues, or total variable costs. TL(w,y,t) corresponds to the translog function of input prices (w), output quantities (y), and time (t). vi is a one-sided, half-normally distributed error term, N+(0, б 2), and є represents a two-sided error term for each bank

v i

i = 1...N. The distributional properties of the one-sided error term have little impact on the estimated efficiency ranks (e.g. ^{Kumbhakar and Lovell, 2003})¹². Thus, v = − lnγ, v = − ln ŋ , or v = lnƟ capture profit, revenue, or cost inefficiencies, respectively.

4. Empirical Results

Tables I and ^II present the estimation results for the time-to-failure hazard model. The dependent variable is time-to-failure. A positive coefficient indicates that an increase in its accompanying variable is associated with an increase in the probability of failure. Each column corresponds to a different regression. Regression (1) uses the composite profit efficiency measure as a proxy for managerial efficiency. Regressions (2), (3), and (4) do the same using non-standard profit, revenue, and cost efficiencies, respectively.

Managerial efficiency is negatively related to bank failures. The coefficients for profit (columns 1 and 2) and revenue efficiency measures (column 3) are significant and negative. Contrary to ^{Wheelock and Wilson (2000}), the coefficient associated with cost efficiency (column 4) is insignificant. Since our study covers a different sample period it indicates a shift in bank managerial strategies during the past decade. Relatively more revenueand profit-efficient banks have a lower probability of failure.

The qualitative results regarding the proxies for the other CAMELS ratings are robust across the four specifications. Robustness checks (not reported) including different sets of explanatory variables give similar results. As expected, non-performing loans and loan loss provisions are positively related to bank failure probabilities. Further, banks whose loans represent a high proportion of their assets are also more likely to fail. Real estate loans and commercial and industrial loans increase the probability of bank failures. In addition, off-balance sheet activities, which were prominent in recent discussions on risk-taking behavior at banks, are unrelated to the bank failure probability. This latter

Table I: Time-to-Failure Hazard Regressions: Left-hand-side Variable is Time-to-Failure. 

Table II Time-to-Failure Hazard Regressions: Left-hand-side Variable is Time-to-Failure. 

result is robust to different measures of off-balance sheet activities.

The coefficient associated with funding liquidity (total loans/ total assets) is positive and significant across all regressions. A higher coefficient implies a higher probability of failure. Thus, it indicates that banks that heavily rely on short-term funding are more likely to fail. It also may indicate that deposit insurance increases the banks' incentive to fund their operations using short-term borrowing.

We also conducted some robustness checks using static classification models (Probit and Tobit). The results for the Probit model are reported in Table III (The logit models give almost identical results). In those regressions all efficiency measures are significant and negatively associated with the probability of bank failure. However, as pointed out above, given the superior properties of hazard models to estimate the risk of failure, we favor the results presented in Tables I and ^II.

Overall our empirical evidence support our main hypothesis. Managerial efficiency, as proxied by profit efficiency, is positively correlated with the probability of bank failures and has independent explanatory power beyond the traditional factors associated with bank failures-CAMELS factors.

5. Conclusions

As a consequence of the 2007-2009 U.S. financial crisis, 322 U.S. commercial banks failed between 2008 and 2010. According to the FDIC estimates, both the number of bank failures and their associated cost increased tenfold compared to the years between 2000 and 2007. Despite the severity of the recent crisis, the number of bank failures was low compared to previous decades. For instance, from 1980 to 1989, 1,467 U.S. commercial banks failed, and from 1990 to 1999 this number was 436. The natural question arising from these facts is what was different this time around.

In this paper we investigate the role played by managerial efficiency in the non-systemic bank failures during the crisis and compare our empirical results to those available for previous waves of bank failures in the U.S.. Using data from 2001 to 2010, we show that profit efficiency-our proxy for managerial efficiency- is a robust predictor of the ability of a bank to survive the crisis. As expected, traditional measures used in the literature as proxies for CAMELS components are highly

Table III: Probit Regressions: Left Hand Side Variable is Failure. 

correlated with the probability of bank failures. After controlling for these factors, we find that profit efficiency has additional explanatory power and should be taken into account in studies investigating the determinants of bank failures.

In contrast to previous crises, this time around cost efficiency was unrelated to bank failures. During previous waves of bank failures, cost-inefficient banks and banks with relatively less capital or low-quality assets were more likely to fail. We find, however, that during the recent crisis capital adequacy lost importance in predicting non-systemic bank failures, while loan quality remained a strong predictor. Our results suggest that profit efficiency can be an important managerial indicator in monitoring the quality of managerial practices and the overall soundness of U.S. commercial banks.