1. INTRODUCCIÓN
Hoy en día, la tecnología de reconstrucción de modelos 3D, usando escáneres de rango está siendo ampliamente aplicada en muchas áreas, tales como: la industria, la ingeniería inversa, la medicina, la impresión 3D, el prototipado rápido, el arte y cultura, el desarrollo de prótesis, la visión por computador, la fotogrametría entre otras [1-4].
En un mundo tan cambiante como el actual, el mercado se ha dinamizado a tal punto, que la creación de nuevos productos y sus diseños deben ser generados de la manera más rápida posible [5,6]. El uso de los escáneres 3D o de rango, se ha convertido en una solución a las exigencias de la industria en este aspecto, ya que pueden obtener una representación digital de los diseños y su posterior manipulación en menos tiempo, que si se diseñaran estos productos desde cero, como es el caso del Diseño Asistido por Computador (DAC) [7-9]. También en el caso de copiar o reproducir partes de un objeto o mecanismo, del cual no se encuentra la documentación detallada de su diseño, muchas veces, la única alternativa es realizar una copia digital para su posterior reproducción. Otros casos de uso pueden ser la utilización de la tecnología del escaneo 3D, para el desarrollo de prótesis para personas en situación de discapacidad, la planificación de una operación, y hasta el desarrollo de modelos 3D para efectos especiales en la industria del cine, así como la creación de juguetes y video juegos, la inspección visual en la industria, la planeación de rutas robóticas, llegando hasta la conservación de la herencia cultural como monumentos y esculturas. Ruiz [10], en su proyecto de investigación mostró la importancia y los beneficios de agregar conocimientos académicos al proceso empírico de diseñar carrozas, el cual puede ser un campo interesante para la generación y aplicación de modelos 3D. Son muchas más los campos de aplicación de la digitalización 3D, lo que demuestra su relevancia en la actualidad [2,11-13].
Todos estos son ejemplos de las áreas que están haciendo uso de la digitalización 3D para la obtención de modelos y sus respectivos usos: desde la decoración hasta la arquitectura, pasando por el desarrollo de prototipos hasta la generación de próstesis para el cuerpo humano como reemplazo o solución a amputaciones. Por ello, cada día más se hace necesaria la impresión en 3D en cualquiera de sus presentaciones [1,3]. El avance tecnológico en los dispositivos de escaneo en la actualidad puede llegar a generar nubes de puntos muy densas (miles o millones de puntos), [4] por el nivel de detalle que pueden llegar al capturar la superficie del objeto escaneado acercándose muy fielmente a la realidad.
Pero el problema de la gran mayoría de las técnicas actuales se basa en que las herramientas o procesos para efectuar una impresión 3D de calidad son muy costosos [1], siendo el tamaño y la resolución del objeto (a veces hasta el color) los factores que aumentan el precio del mismo. Así reducir las características del objeto para alcanzar una aproximación y hacer el proceso de impresión más económico, sería una idea a seguir. Para ello, la resolución del objeto podría darse en términos de cortes, para poder realizar una impresión a diferentes resoluciones. Lo que se pretende en con este trabajo, es la creación de una herramienta sencilla y útil para la asistencia en el procesamiento y copia de objetos 3D y llevarlos a resoluciones de mayor tamaño para su aplicación en el desarrollo de artesanías y manualidades, utilizando únicamente materiales comunes y fáciles de conseguir.
En este artículo se describe un sencillo método basado en algoritmos matemáticos [14,15] y estadísticos [16] para generar diferentes cortes sobre un objeto y, aprovechando la nube de puntos que la representa, pueden ser variables en tamaño para posibilitar la reproducción del objeto en gran formato. Esto es posible lanzando n planos a lo largo de la figura y proyectando los puntos que caen en cierta área de un plano para lograr una estructura de dos dimensiones y analizarlo como un corte. Este último será mostrado como una especie de rebanada de la figura. Asimismo, se reduce (dependiendo qué tan grande sean) la resolución de la imagen, a continuación, estos cortes pueden ser impresos en diferentes materiales, abriendo la posibilidad a artesanos y artistas de obtener representaciones a gran escala del objeto escaneado, a la vez de ser económicamente viable para la creación de artesanía y obras.
Además, los cortes pueden ser impresos a diferentes tamaños en mucho menor tiempo que lo que duraría una impresora 3D.
En este artículo, se propone un método para generar curvas seccionales directamente desde una nube de puntos. El método calcula curvas seccionales mediante cortes, reducción de puntos y ajuste de curvas. No se tiene en cuenta limitaciones en la distribución y densidad de datos en la nube. No obstante, los datos capturados por la mayoría de los dispositivos sin contacto son demasiado densos, están distribuidos aleatoriamente y parcialmente superpuestos. Aunque el método propuesto no es un proceso totalmente automático, es lo suficientemente simple y preciso si los parámetros definidos por el usuario se seleccionan correctamente.
El método propuesto, se compone de las siguientes etapas: la primera etapa se centra en cómo calcular la orientación de la figura por medio de varios procesos estadísticos sobre la nube de puntos.
La siguiente etapa, es lanzar los cortes a lo largo de la figura y conseguir los puntos pertenecientes a cada corte. En la última etapa, se proyectan sobre los planos (que serán posteriormente impresos) y por último, se muestran sólidos en 3D por medio de una herramienta de desarrollo 3D digital.
2. METODOLOGÍA
El prototipado rápido (RP) es un método de fabricación en crecimiento en el que una copia de un objeto diseñado es producida capa por capa. RP es actualmente una técnica de fabricación para crear modelos de objetos físicos complejos en un tiempo más corto que los de los métodos de fabricación de prototipos más tradicionales. Como el proceso RP requiere contornos seccionales perpendiculares a la dirección del eje, el modelo CAD o los puntos de datos deben seccionarse en forma de capas delgadas a partir de las cuales se determinan las curvas de contorno seccionales. Para lograr un prototipo preciso, estas curvas de contorno se deben determinar con la mayor precisión posible. Es por esto que en esta sección se describen los pasos para tomar una nube de puntos y cortarlas en secciones transversales para luego obtener contornos seccionales para su posterior impresión, en un material determinado (poliestireno, madera, etc.). En la figura 1, se esquematiza el método en este artículo.
2.1 Orientación de la figura
El cálculo de la mayor tendencia en dirección de los puntos de la figura se obtiene por medio del proceso PCA (Principal Component Analysis, Análisis de Componentes Principales) [17,18]. Este genera una matriz nxn, llamada matriz de covarianza A (ecuación 1) [17,19], donde n es la dimensión de los puntos que componen la nube, en este caso, será 3. La matriz de covarianza A, engloba tres vectores principales. El primero es para indicar la tendencia mayor del conjunto de puntos (figura 2a), el segundo es la segunda tendencia (figura 2b) y la tercera es un vector perpendicular a los dos primeros (figura 2c), dejando ver un sistema de coordenadas 3D sobre la imagen tridimensional. La función cov (,), indica la covarianza entre las variables que se encuentran entre los paréntesis.
2.2 Identificación de la caja delimitadora
Con estos tres elementos de tres dimensiones, se pueden calcular 6 puntos claves de la figura, los que corresponden los más alejados en las direcciones de los vectores: el más alto, el más bajo, el más cercano, el más lejano, el más a la izquierda y el más a la derecha (figura 3) (dejando claro que, como la orientación de la figura no es trivial y no coincide con ningún eje obligatoriamente, los términos anteriormente descritos como “arriba”, “abajo”, etc., son llamados así solo para darles un significado a los puntos de la figura, más no significan que esté “abajo” el punto, por ejemplo) y así hallar el “bounding box”, que corresponde a una caja imaginaria que encierra la totalidad de la figura. Esta caja define también el tamaño de los cortes para que, al momento de la impresión, se pueda convertir de unidades virtuales (aquellas definidas por los puntos de la figura) a unidades tangibles como centímetros, pulgadas, etc.
2.3 Cálculo de planos
El siguiente paso es calcular los planos que denotarán la esencia de los cortes, los cuales serán “lanzados” desde el punto más “bajo” de la figura (que coincide con la base de la caja delimitadora) hasta el punto más alto (igual a la tapa superior de la caja que la contiene) a una distancia d constante a lo largo de la figura 3. Los planos tienen la misma área que la base de la caja y por ende ningún punto queda por fuera. Ahora se agrupan los puntos de la nube tomando como guía los planos que ya han sido lanzados.
2.4 Proyección de puntos sobre los planos
Cada plano tiene un área definida a d/2 de distancia (sabiendo que d es la distancia entre dos planos consecutivos figura 4) en la que todos los puntos que caigan pertenecerán al corte definido por el plano en mención.
Esta región ha sido definida como la mitad de la distancia entre dos planos consecutivos hacia arriba y la misma longitud hacia abajo (dos direcciones diferentes en las que el vector principal calculado por PCA es la orientación) para garantizar que ningún punto quede por fuera y no tenga un corte asignado (figura 4).
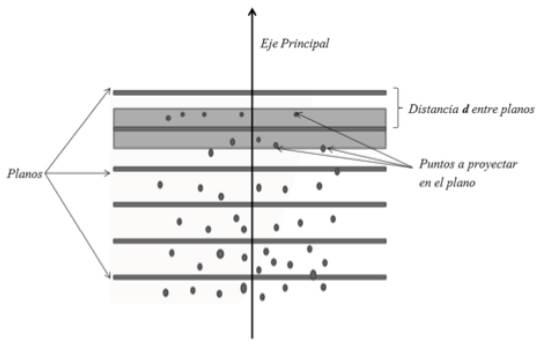
Figure 4 Consecutive Planes at a same distance between them, with area (gray band). Each area contains points that will be projected into the corresponding plane.
Teniendo los planos calculados y establecido las distancias d/2 entre planos, cada uno de los puntos que este entre dichas distancias (área gris oscura figura 4), se proyectarán al plano. La proyección se calcula utilizando el conjunto de ecuaciones 2-7, entre las cuales están la ecuación del plano (3), el punto a proyectar P (2), el punto proyectado P’ (3) y las ecuaciones de proyección 5, 6 y 7.
Una vez proyectados los puntos se interpolan para obtener los contornos suaves como en la figura 5.
En las ecuaciones anteriores P es el punto a proyectar, Pi es el plano definido por las constantes A, B, C y D, y x’, y’ y z’ son las coordenadas del nuevo punto proyectado.
Para poder imprimir estos puntos hay que ver en la misma dirección que el vector principal proporciona y analizarlos como objetos en 2D pero sin ignorar que son 3D. Su conversión a figuras bidimensionales es un trabajo geométrico que aplica dos rotaciones sobre el eje principal para alinearlo al eje Z y así despreciar esta coordenada. Las rotaciones necesarias para lograr este efecto sobre el vector que determina la orientación de la figura, se les aplica también a todos los puntos de la imagen para alinearlos igualmente a despreciar Z y, así, tomar solo X y Y de los puntos en 3D como las únicas coordenadas relevantes en 2D [2]. Estas figuras ya engloban una silueta que se puede llevar a cualquier medio de impresión común y tener los contornos fácilmente de cada uno de los cortes [20].
2.5 Despliegue de cortes en 3D
Para mostrar los cortes, y en general la figura tal como quedaría si el proceso de impresión se llevará a cabo (teniendo en cuenta las medidas calculadas por reglas de 3 aplicadas sobre la distancia d y el bounding box), se realiza una vista previa para desplegar digitalmente la imagen utilizando la librería gráfica OpenGL, la cual también se utilizará para el despliegue y procesamiento 3D del objeto a visualizar [6].
Para hacer que los cortes se visualicen sólidos, se duplica la cantidad de puntos por corte. Al tener dos grupos de puntos por cada corte, uno se traslada 𝑑/2 unidades hacia arriba y el otro la misma distancia hacia dirección contraria (igualmente tomando como orientación el eje principal de la figura) generando, así, dos planos más considerados como la tapa superior y la tapa inferior. Estas tapas coinciden con las de los planos consiguientes tanto arriba como abajo, exceptuando los cortes más extremos, que solo tienen un corte inmediato.
Aprovechando las características de OpenGL, se manejan las primitivas TRIANGLE_STRIP y TRIANGLE_ FAN [6] para generar el contorno lateral y las tapas del corte, respectivamente. La primera primitiva mencionada recibe una serie de puntos y cada tres valores se arma un triángulo, a cada uno calculando la normal para efectos de luz de OpenGL [7]. Esta normal se calcula usando la ecuación 8 y se ejemplificad en la figura 6.
La segunda primitiva mencionada es utilizada en las tapas superior e inferior del corte, y recibe un primer punto como centroide y el resto de puntos va generando triángulos con uno de los vértices siendo el primero definido [6]. La normal para ambos casos es un vector que comienza en el centroide del corte y termina en un punto a una distancia normalizada (igual a uno) y resulta paralelo al eje principal de la figura.
Y de esta forma se podrá representar la figura virtualmente como cortes contiguos entre sí.
3. RESULTADOS Y DISCUSIÓN
El algoritmo entero fue desarrollado en C#.NET sobre un computador con Windows 10 de 64 bits, procesador Intel Celeron de 2.60 GHz y 4.0 GB de memoria RAM.

Figure 7 a) Real object, b) object in scanning process, c) digital object, d) object reproduced in foam.
La figura escaneada 7a mide 8 cm de alto. Se escaneó usando el scanner Shinning 3D que consta del cabezal que reconoce la figura y la mesa rotatoria que permite observarla en diferentes ángulos (figura 7b) y se pudo reproducir con 25 cortes de 1 cm de alto cada uno (en total, 25 cm de alto), como se observa en las figuras 7c y 7d.
La plataforma desarrollada en este proyecto, la cual es nombrada como IP3D, compite con dos herramientas actualmente en el mercado (MeshLab y Three.js Editor) en la carga de figuras medidas por la cantidad de puntos y la velocidad de despliegue. Los resultados pueden observarse en la figura 8:
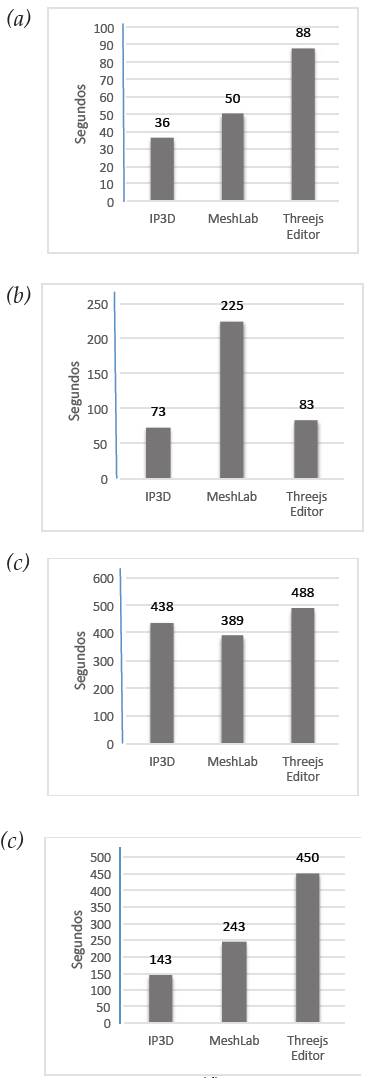
Figure 8 a) Load velocities comparison with 15090 points, b) 229356 points, c) 2103546 points, d) 454044 points.
Sin duda estos son valores que muestran que la plataforma y los algoritmos desarrollados en mención, mejoran en la parte de carga del objeto comparados con las dos herramientas del mercado. Por otra parte, están los tiempos de carga de cortes que, por no tener aproximaciones que hagan algo similar, se optó por evaluar el rendimiento creciendo el número de puntos de la figura linealmente.
Los resultados del procesamiento del objeto fueron medidos manualmente y se obtuvieron los siguientes valores comprobando que el algoritmo de cálculo de cortes es linealmente creciente a medida que la cantidad de puntos aumenta (figura 9):
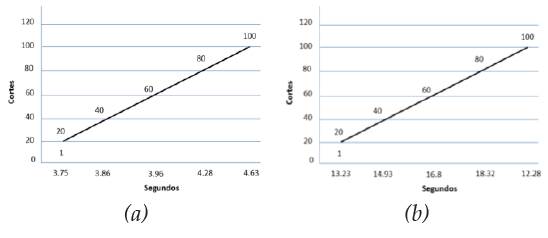
Figure 9 a) Performance test with 4545044 points between 20 and 100 slices, b) 1963392 points between 20 and 100.
Varias ideas iban surgiendo cuando se desarrollaba este método, relacionados con el procesamiento de los puntos ya en dos dimensiones como son la clusterización de puntos para figuras que tengan varios cortes en un plano (algoritmo que se desarrolló pero su complejidad no permite la eficiente operación para figuras con un conjunto de puntos mayor a 200.000), el cálculo de los puntos externos de la figura y la unión de los puntos por curvas NURBS [23-26], las cuales permitirán mayor ampliación de los cortes y, por ende, mejor resolución a gran escala de la figura.
Existen aproximaciones de aplicativos y métodos que intentan hacer este mismo proceso, pero se basan en el contorno obtenido de las figuras al momento de los cortes por planos. De esta forma, el cálculo de los cortes puede ser más rápido, pero al momento de querer cambiar la resolución, el número o el tamaño de los cortes, son poco eficientes porque tienen que trabajar sobre toda la figura y nuevamente generar dichos contornos.
Rodrigo Minetto y colaboradores [27] comparten el mismo flujo de trabajo que el propuesto por el presente artículo: 1. Escoger el eje guía para desplazar los cortes, 2. Calcular los cortes sobre el eje escogido, 3. Reconstrucción del contorno en 2D del corte y 4. Determinar la densidad de los cortes. Cada paso difiere en la metodología usada, sobre todo el cuarto paso, el cual puede ser intercambiable con el segundo, es decir, el método de este artículo recibe la densidad de los cortes (la cual es igual para todos sobre la figura), luego los calcula y por último, reconstruye el contorno de los mismos.
El método propuesto no suaviza las superficies laterales, porque se tiene la idea de mantener los cortes extraídos desde el material sin importar su moldeamiento en los lados. Sin embargo, queda abierta la idea de combinar este método con el propuesto en [16] para delinear los extremos de los cortes y hacerlo más real a la figura original. Para ello se podrían analizar los otros vectores principales que arroja el PCA y encontrar diferentes caras para un mismo corte.
4. CONCLUSIONES
En este artículo se propuso un método para generar curvas de contorno a partir de una nube de puntos para la creación de prototipado rápido para el procesamiento y copia de objetos 3D. El método propuesto corta directamente la nube de puntos, sin necesidad de utilizar representaciones intermedias como una malla triangular o representaciones volumétricas; para ello los datos de la nube se segmentan en varias capas a lo largo de la dirección principal dada por el Análisis de Componentes Principales, los puntos entre cortes se proyectan a un plano de regresión y se construye un polígono para que se ajuste mejor a los puntos. El grosor de cada capa se establece de modo que el error de superficie se mantiene justo dentro de un límite dado. El algoritmo ha sido implementado con C# en la plataforma OpenGL.
Como se evidenció en las métricas de rendimiento de los algoritmos involucrados en este nuevo método, nos muestran que además de simple, es rápido y eficiente respecto a software del mercado como MeshLab y Three.js Editor. En cuanto a la resolución de la figura, puede variarse y aplicarse un gran número de cortes para alcanzar mayor definición y asemejarse cada vez más a la realidad.
Finalmente, se abre un gran abanico de opciones relacionado con los materiales que pueden ser utilizados la reproducción del objeto.
Como trabajo futuro queda determinar la tolerancia del ancho de cada corte con mayor precisión, de modo que el algoritmo de construcción de la curva de ajuste a los puntos sea más preciso.






















