Firm Entry and Productivity Turnovers in Import Substituting Markets: Evidence from the Petrochemical Industry in Colombia

Entrada de firmas y rotación de la productividad en mercados sustitutivos de importaciones: evidencia de la industria petroquímica en Colombia

Entrée de firmes et rotation de la productivité sur des marchés substitutifs d'importation: une évidence de l'industrie pétrochimique en Colombie

Luis H. Gutiérrez y Carlos Pombo

Luis H. Gutiérrez. Associate Professor, Department of Economics, Universidad del Rosario, Bogotá. Carlos Pombo. Associate Professor, Department of Economics, Universidad del Rosario, Bogotá E-mail: capombo@urosario.edu.co (C. Pombo); Fax: +571-3445763. Financial support from the Fundación para la Promoción de la Ciencia y la Tecnología del Banco de la República is gratefully acknowledged. We want to thank Rodrigo Taborda for his research assistance. We also benefited from the comments of Luis Eduardo Fajardo, and the participants of the XXII Latin American Meeting of the Econometric Society, Santiago de Chile (2004).

-Introduction. -I. Patterns of Plant Entry. -II. Data and Methodology. -III. Productivity Differentials and Turnovers. -IV. The Econometrics of Entry Rates -V. Conclusions. -Annex. -References.

Primera versión recibida en noviembre de 2004; versión final aceptada en junio de 2005 (eds.)

Resumen: El artículo analiza la entrada de firmas y rotación de la productividad promedio en la industria petroquímica colombiana para el período 1974-1998. Los resultados muestran que los entrantes exitosos dieron forma a la productividad de la industria e indujeron a la reestructuración de las plantas existentes. Los flujos de entrada crecieron constantemente en el sector de plásticos, a pesar de los cambios de política comercial. La descomposición del crecimiento de la productividad total de los factores muestra que el efecto de las empresas establecidas domina sobre el efecto de rotación de empresas. Los resultados econométricos sugieren que las barreras a la entrada, asociadas con el licenciamiento de la tecnología y la dependencia de materias primas importadas disuaden la entrada, mientras que variables complementarias del mercado como los niveles de productividad, crecimiento en la construcción de vivienda y competencia periférica inducen la entrada de firmas.
Palabras clave: Entrada, rotación, productividad total factorial, industria petroquímica. Clasificación JEL: O12, D24, O47

Abstract: This paper analyses plant entry and productivity turnovers across Colombia's petrochemical industry for the 1974-1998 period. Results show that successful entrants shaped industry productivity and induced plant restructuring among incumbent plants. Entry flows increased steadily within plastics and boosted after trade liberalization. Total factor productivity growth decomposition shows that the incumbent effect dominates the turnover effect. Econometric results suggest that barriers to entry associated with plant technology licensing and dependence of imported raw materials deter entry while complementary market variables such as industry productivity levels, growth in housing construction, and fringe competition induce firm entry.
Key Words: Entry, turnover, total factor productivity, petrochemical industry. JEL classification: O12, D24, O47

Résumé: L'article analyse l'entrée de firmes et la rotation de la productivité moyenne dans l'industrie pétrochimique colombienne pour le période entre 1974 et 1998. Les résultats montrent que les entreprises entrantes qui ont eu du succès, ont donné forme à la productivité de l'industrie, et qu'ils ont induit à la restructuration des usines existantes. Les flux d'entrée ont constamment grandi dans le secteur des plastiques, malgré les changements de politique commerciale. La décomposition de la croissance de la productivité totale des facteurs montre que l'effet des entreprises établies domine sur l'effet de rotation d'entreprises. Les résultats des estimations économétriques suggèrent que les barrières à l'entrée, associées aux autorisations d'utilisation de la technologie et à la dépendance de matières premières importées, dissuadent l'entrée, tandis que des variables complémentaires du marché, comme les niveaux de productivité, la croissance dans le secteur de la construction de logement et la concurrence périphérique, induisent l'entrée des firmes.
Mots clés: Entrée, rotation, productivité totale factorielle, l'industrie pétrochimique. Codes JEL: O12, D24, O47

Introduction

The petrochemical industry worldwide is formed by vertically-integrated firms. They manufacture intermediate materials derived from the oil refinement and liquid gas industries that are essential in the manufacture of end products in several industries such as textiles, apparel, domestic appliances, transportation equipment, and housing construction among many others. This industry is intensive in physical capital and along with pharmaceuticals it is also intensive in research and development. Plastics are the most dynamic sub-groups representing around 60% of the industrial uses within petrochemicals because they are close cheap substitutes of other materials currently used in the manufacture of a variety of final goods. On the other hand, production of basic chemicals in Latin America is dominated by multinational enterprises that entered developing markets during the import substituting industrialization years from the 50s to the 70s in Latin America.

Two types of promoting strategies were implemented in the region. One was the Brazilian-type strategy, which relied on attracting massive direct foreign investment and multinationals through granting non-market entry barriers via tariff protection. Once those firms settled in the market they were expected to pass technological transfers to downstream local industries. The other was the Andean-type (Colombia-Venezuela) strategy, much less aggressive, perhaps because of their domestic market size, that relied both on developing a local basic-chemical industry dependent of crude oil and oil refinement, along with the promotion of foreign direct investment. Several economic policy instruments were used in Colombia three decades ago to promote import-substituting industries such as import licenses, tariffs, tax exceptions applied to specific industries, long-term credits with implicit subsidies, and the direct involvement of government credit institutions in the setup of industrial projects.

Empirical studies on firm entry and turnovers have been focused on the evidence of the OECD cases. The study of Dunne, Roberts, & Samuelson (1988) for the US manufacturing industry is still the most comprehensive country study ever made. Afterwards, there have been just a few efforts in studying firm-level entry, heterogeneity and productivity for the case of developing economies. The collective work of Roberts & Tybout (1996) is the first comprehensive attempt to gather several cases. They include the cases of Morocco, Chile, Colombia, and Mexico. The study of Colombia only covers the 1978-1988 period. Its results clearly are out of date because it leaves the decade of the nineties where the main commercial reforms took place in Colombia since 1959.

The studies of Levinsohn & Petrin (1999) and Pavnick (2002) use the same dataset of Chile from 1980 to 1986. They evaluate manufacturing productivity using the parametric approach of Olley & Pakes (1996). Both papers are more concerned about the econometric advantages of modeling firm level productivity dynamics through stochastic processes than about providing a story regarding the effect of entry on local market characteristics and industry development. Aw, Cheng, & Roberts (2001) analyzes productivity differentials and plant turnovers for the Taiwanese industry based on three census years. Firm-level productivity is estimated through index number methods. For the case of Colombia the paper of Melendez et. al (2003) is the first in applying the Olley & Pakes approach to estimate firm productivity and then measure plant turnover across main manufacturing industries at ISIC two-digit levels using Haltiwanger's (2001) productivity decomposition.

One general drawback of these studies on firm turnover and productivity excepting Olley & Pakes (1996), is that they report generic analyses presenting aggregate measures at two-digits ISIC code where there is no specific explanation regarding the forces behind plant turnover within industries and, more importantly, on what explains turnover differences across industries. The objective of this paper is three-fold. First, the paper seeks to present an industry case within a semi-industrialized economy in Latin America such as Colombia. The importance of analyzing the petrochemical industry lays down in three reasons: i) as in any developed or developing country it is an industry where barriers to entry may have played a significant role on entry, in particular, scale economies, high fixed costs, and the spending in patented technologies; ii) the development of the petrochemical industry was conditioned by the initial pathway of inward-looking economic development Colombia pursued since the 1950s until the late 1980s. However, the recent export-orientation the industry followed under the economic openness program boosted plant entry; iii) petrochemical industries are intertwined in what we call the petrochemical chain [Annex 2] that introduces an element of plant heterogeneity and productivity differences. Moreover, the technological complexity is increased by the different paths of maturity present in the links along with the petrochemical tree.

Second, the paper seeks to contribute in providing new evidence to shed light on the long-term forces behind entry patterns and plant productivity heterogeneity within an industry with the features above-mentioned. It will so present very detailed plant-level productivity estimations that follow state of the art methodologies. Third, the paper looks to test under a variety of econometric specifications what has determined entry in this industry in the long run.

This study makes an effort in analyzing jointly the patterns of entry, the productivity dynamics, and the explanations of what may determine entry in an industry with such special features. To our best knowledge there is no industry study for a developing economy that has tried to put these three pieces together. Plant-level productivity estimations are less ambitious. They follow standard methodologies following index number methods. Our focus is to provide a complete picture about plant entry and stylized facts, the role of entrants within the industry, plant heterogeneity and productivity differentials, the plant turnover effect on aggregate industry productivity, and the testing of gross entry flows as function of entry barriers and market incentives.

The paper is organized in five additional sections. Section 2 presents an overview of entry patterns and plant survival within the sector for a 25 years span. Section 3 describes the data and presents the main methodological properties and advantages of using exact index numbers in measuring multifactor productivity as well as the productivity turnover decomposition equations. Section 4 reports the productivity differentials by market entry dynamics and also across sub-markets. Section 5 provides the econometric analysis on modeling plant entry determinants following the Orr-type specification. Section 6 concludes the paper and summarizes its results.

I. Patterns of Plant Entry

Empirical research on firm entry, exit and turnovers has been very active since the 70s worldwide. Three comprehensive studies published from 1989 to 1994 present what are the patterns of firm entry and types of competition based on more than 25 case studies. The work of Geroski & Schwalbach (1991) collects 12 studies of firm entry and contestability for OEDC countries and Korea. The 1989 and 1994 special issues of the International Journal of Industrial Organization gather 15 studies of entry barriers and post-entry competition for different industries within the OECD economies.

Caves (1998) presented a survey on new findings about the turnover and mobility of firms where he reviews some stylized facts and tries to see how they fit with existing theories. Perhaps the largest study on a country firm turnover done so far is the study of Dunne, Roberts & Samuelson (1988) for the case of the U.S. They used information at plant-level data from five Censuses of Manufactures for a 20-year span. Baldwin (1995), Baldwin & Gu (2002) and Baldwin et al (2002) have studied plant turnover and the importance of entry into Canadian manufacturing. Both studies make use of data from census of manufactures. Recently Disney, Haskel & Heden (2003) present new results of the dynamics of entry and exit in the United Kingdom.

The main difficulty to undertake that kind of research has been to collect reliable and comprehensive data to measure firm turnover. Almost all research done on the subject has made use of data collected from National censuses. This study uses plant-level data from the Annual Manufacturing Survey of Colombia [Encuesta Anual Manufacturera (EAM)], which covers a 25 year-period ranging from 1974 to 1998.¹

The industry structure is formed by the production of basic materials to their final use in several consumer goods industries. The study sample focuses on two main petrochemical groups that constitute the core activities: synthetic resins, and plastic materials, man-made fibers except glass, and the manufacture of plastic products. Together they represent 5% of manufacturing plants spread in 13 separate markets and industries at ISIC five digits level.²

Table 1 provides a summary of the number of plants by each of the industry sub-groups as well as for the entire sample period. The number of industrial plants grew from a minimum of 178 in 1975 to a maximum of 507 in 1998. Plastics explain on average 92% of total plants in petrochemicals while the remaining is due to synthetic resins. The petrochemical industry, in turn explains on average 38% of the total plants in the chemical industry and 5% of total manufacturing. Hence, trends are increasing for all cases.

Different measures of plant entry have been used trying to approach the patterns of market dynamics. This study follows the methodologies of Dunne et al. (1988), Geroski (1991), Baldwin (1995) and Baldwin et al. (2002). In particular, we used simple indicators of gross entry, entry penetration and non-parametric plant survival rates to describe the entry patterns.

Geroski (1995) states that there are empirical regularities regarding firm entry: i) Entry is common. Large numbers of firms enter most markets in most years, but entry rates are far higher than market penetration rates; ii) Entry and exit rates are highly positively correlated, and net entry rates and penetration are modest fractions of gross entry rates and penetration; iii) the survival rate of most entrants is low, and even successful entrants may take more than a decade to achieve a size comparable to the average incumbent; and iv) entry rates vary over time, coming in waves, which often peak early in the life of many markets. Different waves tend to contain different types of entrant.

Table 1. Petrochemical Industry and Total Manufacturing Average Number of Plants

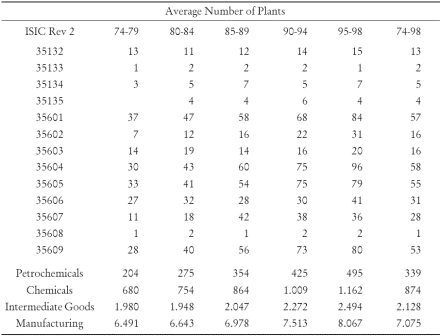
Source: DANE-EAM.

Notes: ISIC 353: Sinthetic Resins; 356: Plastics

Table 2 reports information on gross entry (ERi) for each of the thirteen petrochemical industry groups. There were 586 plant start-ups during the 25 years span and entry was concentrated in plastics, reflecting the fact that this group of industries requires less amount of capital investment and that the technology to enter is standardized. The entry rate exhibits an increase in plastics and remains constant within resins. There is not enough information to compare the data with that found in international studies.³

Three more comments are worth mentioning. First, Gross entry in plastics was concentrated in three sub-industries. They were the manufacture of tubular films and synthetic guts, the manufacture of furniture and plastic products not classified elsewhere and the manufacture of basic plastic shapes, sheets, films and tubing. Almost 300 start-ups took place in them. These are industries with strong links to packing and housing that performed relatively well during all the period.

Second, overall entry in the petrochemical industry does not appear to be cyclical. Exception made for initial years (1974-79) and the years 1990-91, the number of firms entering the market was quite even and not dependent of the overall business cycle. For instance, in the first years of the 1980's, the Colombian economy suffered a slowdown in its economic growth but the number of entrants kept its pace.

Table 2. Entry Plants (units) and Gross Entry Rates (percentages)

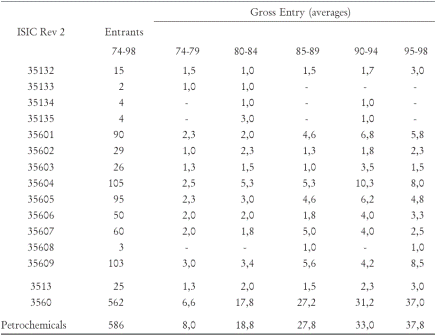
Source: Own estimations based on DANE-EAM.

Methodology: ERt = NEt /NTt ; where NE= number of entrants in ISIC-group i at year t; NT= total number of plants in ISIC-group i at year t.

Third, the data seems to confirm the hypothesis that plant entry was boosted after the economic liberalization of 1991. The annual number of start-ups was 35 between during the decade against the average of 18 startups between 1974 and 1989 where there was a standing policy of tariff protection.

Table 3 summarizes the measures of penetration rates. The measures indicate low penetration rates, that is, the weight of entrants' output is a small fraction relative to incumbents. This signals also plant size. Entrants are small firms with higher plant minimal efficiency scales. The long run average for the entire industry is 6.8% when rates are weighted by plant output market share. The plastic industry exhibit rates, where on average entrants explain 5% of its group output. In resins despite the lower entry rates new plants explain 16% of its sector output. These numbers are consistent with findings of other studies on firm entry. For instance, Cable & Schwalbach (1991) reports penetration rates for seven OECD countries and Korea across manufacturing groups covering different periods in the 70s and 80s. For the chemical industry Portugal has a 33% penetration rate, followed by the US with a rate of 19%. The remaining cases, entry penetration rates range for 1.5% to 6%. Therefore, one can claim that the first stylized fact applies to the petrochemical industry. Gross entry is a common economic force, averaging 24 firms during 1974-1998, and entry rates are larger than penetration rates.

The Survival rate of entering plants is another feature that characterizes entry patterns within an industry. Figure 1 shows the evolution of such rates with plant ageing.⁴ The figure was reached by summing up the number of firms that survive across each cohort, and dividing it by the total number of entrants. It is clear that as firms age their survival likelihood declines. Some facts can be noticed. First, a very low number of plants die during the first two years of birth, meaning that new firms adopt tough competition strategies. The average life span of new firms is high. It takes about seven years to get a survival indicator of less than 50%. Mata (1995) shows a figure of the survival schedule of new plants in Portugal. The shape of the function is convex, which implies an increasing rate of firm deaths. In a similar way, the shape of the function for the samples of Colombian petrochemicals firms is also convex, implying the same behavior.⁵

Table 3.Entrant Market Share

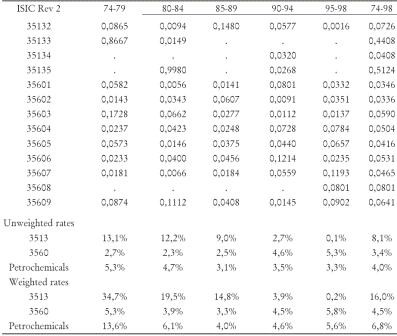
Source: Own estimations based on DANE-EAM

Methodology: Entrant Market Share (Penetration rate) in sector i, is equal to: ESt=QEt/QTt ; where ES = entrants' share at year t ; QE = entrants' output; QT = Total ISIC-group output.

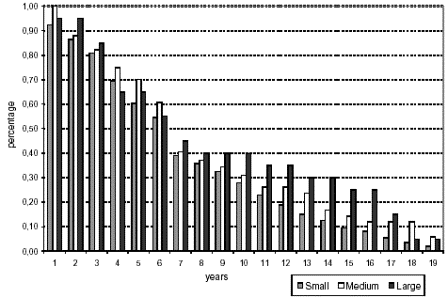
Another fact is that for plants that passed the rule their survival was high. To illustrate this, about 80% survived on average between five to ten years, and almost 61% survive between ten to fifteen years. Measures of survival rates across cohorts showed that plants that belong to the 1975-1979 cohorts had a lower percentage of continuing firms. Plants born in the 1980s had a superior performance. It is still too early to evaluate comparatively the survival of the cohorts born in the 1990s; the data seems to show a slightly lower pattern.⁶ Another important feature is the extent to which small-size plants are more likely to fail than larger-size firms. Figure 2 gives the survival patterns by plant size. One can sees that the patterns hold regardless plant size. Despite of small plants have the lowest survival rates they are not significant different that those from medium and large size plants. For instance, 61 percent of small size entrants size entrants during the first seven years of commercial operations. This numbers are similar to medium size plants [59%] and large size plants [55%]. Thus, ex-post entry competition is not affected by size. This finding is also proven in the econometric analysis of entry flows.

In sum, the highlighted entry patterns indicate that the results fit along the expected direction and magnitudes, relative to what other studies have found within the chemical industry. Thus, the gross entry penetration rates are low. The analyzed sample gives no evidence of the existence of either entry or exit waves (shake-out). The next section turns attention to the analysis of plant productivity by entry dynamics.

Figure 1. Plant survival rates

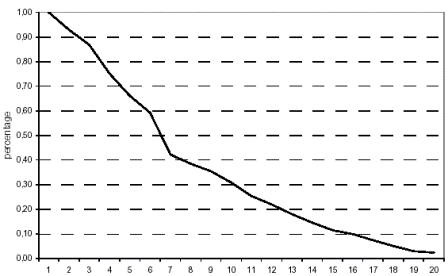
Figure 2. Survival rates by plant size

II. Data and Methodology

A. Data

The analysis of plant productivity is based on a longitudinal dataset that includes all plants that report consistently at the Colombia's Annual Manufacturing Survey [Encuesta Anual Manufacturera (EAM)] for the 1975-1998 period. There were 921 identified plants that at some point have records at the survey within the plastic and synthetic resins sectors. Nonetheless, 298 plants were dropped form the panel for several data inconsistencies and then were classified as volatiles. The exclusion of those plants reduces the number of plants to 623 in the working panel. This final panel is slightly different from the one used in section II to measure entry and exit rates. The objective here is to work with individuals that have consistent records in the basic variables of output, investment, labor input, materials and power consumption that allow us getting accurate measures of input demands and total factor productivity indices.⁷

The EAM until 1977 published the variable of plant startup year. Later we consider as the startup year the first record that shows up in the panel. The exit date is the year by which there are no records afterwards. Therefore, plants were classified according to entry dynamics. Incumbents are plants that show records for the entire period, entrants are surviving plants that begun operations after 1977 and are still active in 1998, and the existing plants are those founded before 1977 or entrants after 1977 that exit the market before 1998.

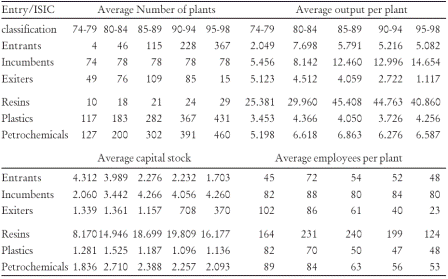
Table 4 depicts the basic characteristics of the working dataset given by the average number of plants, average plant output, capital stock, and employment within by five-year periods. There are several features worth highlighting. To begin with there is a notorious difference in capital intensity between the two industry branches. On average, the capital stock per plant in synthetic resins moved 6.3 in the 70s to 14.2 times at the end of the 1990s. Plant size is on average 3.5 times larger in resins, given by the number of employees. In both cases plant size started decreasing since 1990 in both sectors. This adjustment suggests labor restructuring within plants to minimal efficiency scales. The above differences also hold for type of plants according to entry dynamics. Incumbents tend to use more capital-intensive technologies and plants are larger in size and in their operative scale. On average, plant output for incumbent plants is 2.5 times larger than for entering plants. In contrasts, exiting plants show decreasing patterns in their characteristic variables.

Table 4. Dataset Charactheristics

Source: Own estimation based on DANE-EAM

Notes: ISIC 3513 = Synthetic Resins; ISIC 3560 = Plastics; Petrochemicals = 3513 + 3560; value series are in millions of pesos at 1998 prices.

B. Methodology

We followed an index numbers approach to measure plant total factor productivity instead of following the parametric methodology of Olley & Pakes (1996) or the refinement through the usage of instrumental variables suggested by Levison & Petrin (2004), who model plant productivity dynamics though a first order stochastic Markov process. The studies that have relied on this methodology based on data on developing economies have the shortcoming of assuming continuous investment spending series at plant level since a first order Markov-process of a firm's investment decisions depend on the past productivity shocks. This outcome is delivered implied from Olley & Pakes paper. The methodology was designed to characterize the telecom equipment industry in the US where the assumption of continuous investment is realistic, in particular after market deregulation of the 1980s. One fact that is common in manufacturing in developing economies is the deterministic characteristic of investment in fixed assets. The non-parametric approach overcomes the above problem although this methodology is less robust than any classic parametric estimation based on costs or production functions, because one is deriving the dual rather than the primal rate of technical change.

Our productivity measures rely on translog indices that have well-known economic properties such as being an exact transformation of a translog production technology. The index is also time-chained, which allows factor shares to change over time. This feature makes it unnecessary to assume neutrality in technical progress under the hypothesis of perfect competition. Changes in input value shares will be the result of changes in factor marginal rates of substitution.⁸ The Translog index of TFP growth for any given firm is usually defined as

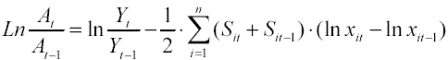(1)

where: si = factor i's share in gross output at time t; xi = type of input i; At = Hicks-neutral index of technical change at time t; and Yt = firm gross output at time t.

It follows that under the classical assumptions the rate of growth of TFP is equivalent to the rate of technical progress. The underlying technology of (1) is the restricted Translog production function under constant returns to scale.⁹ A common refinement to the Translog index is to take into account the effects of changes in quality in inputs Jorgenson & Griliches (1967), in which aggregate inputs follow a translog specification in each one of its components. Under the assumption of CRTS, the translog index for each input i becomes

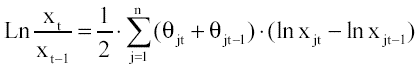(2)

where x = capital, labor, and intermediate materials. Electricity consumption was treated as independent input since it can not be divide in two or more components.¹⁰

Equations (1) and (2) constitute the baseline to generate TFP indices as well as a starting point in undertaking an analysis of sources of growth for each one of the 623 plants of the final working-sample. Traditional growth accounting exercises based on the above TFP decomposition or its extensions that relax the core assumptions of perfect competition, long run firm optimization, non-externalities, or equal efficiency across capital vintages have the shortcoming that those TFP decompositions do not take into account for the effect of market entry and exit in overall industry productivity. Firm entry is an endogenous flow that shifts either plant or industry-group productivity.¹¹

The analysis of plant-productivity turnover has attracted attention within the productivity literature in recent years because economies around the world have engaged in a series of structural market reforms that have implied market deregulation, elimination of entry barriers and promotion of market competition since the 1990s. Firm entry has an effect on plant reallocation and shakeout of inefficient firms. These effects in fact might induce plant restructuring. Thus, entry and exit flows force firms to become more productive over time in order to survive. Enterprises that cannot make it fail end exit the market. The non-parametric estimation of a given industry group productivity index level can be defined as the weighted sum of firm productivity level at year t:

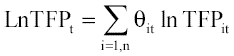(3)

where i indices plants, TFP is the translog index derived from Eq. (1), and is plant weight in industry-ISIC specific gross output. This formulation is interesting from the view of output reallocation across firms. In particular, if high productivity firms gain participation this will contribute positively to industry productivity growth even if no individual firm experiences a productivity increase. The above fact is called as firm-productivity turnovers.

In the literature on turnovers there are two approaches in measuring the overall output and input reallocation effects. One is in levels following Olley & Pakes (1996) formula. An alternative TFP decomposition focuses on the measurement of productivity growth according to entry dynamics following Griliches & Regev (1995). This decomposition defines the contributions of continuing firms, the difference in average between entering and exiting cohorts and reallocation of market shares into the TFP residual among all plants. In particular, if high productivity firms gain participation this will contribute positively to industry productivity growth even if no individual firm experiences a productivity increase. Taking differences of (3) one can express changes in productivity over time for a single plant i as

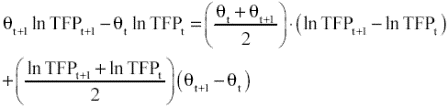(4)

Equation (4) says that the contribution of plant i to an industry productivity growth is the sum of two components: i) the weighted own productivity growth by market share, and ii) the change in its market share weighted its productivity average. If there is no entry or exit at time t and t+1, this implies that industry productivity will equal the sum of productivities over all plants given equation (4). An increase in market reallocation from low productivity to high productivity firms and/or a single firm productivity increase will explain industry productivity growth under this decomposition. Now, if entry or exit takes place, the above-mentioned set up is not longer useful. The shortcut that Griliches & Regev (1995) proposed is to aggregate in a given two-year period all entrants (E) at year t+1 and all dying plants (D) at year t as a single firm with weight in output or sales and respectively. Aggregating over continuing firms and adding firm entrant and exit effects, industry productivity growth can be approximated by the following TFP decomposition equation:¹²

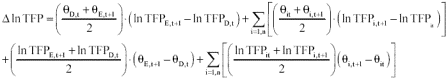(5)

The above formula decomposes an industry ISIC-group productivity growth in four parts: i) the turnover effect between entrants and dying firms, ii) the contribution of continuing plants, iii) the market share reallocation among entrants and existing firms, and iv) the market share reallocation from low to high productivity of continuing firms. The last two terms can be simply added to denote market share reallocation effect. Thus we applied the formula (5) to measure plant productivity turnovers across the thirteen petrochemical markets for the 1975-1998 period. Next section presents the results regarding plant-productivity differential among entrants, incumbents and exiting plants, as well as how much the reallocation effect from low to high productive plants explains overall productivity within the resins and plastics industries.

III. Productivity Differentials and Turnovers

Market entry influences industry cycles, restructuring processes, and transitions. This section presents a comparative analysis of productivity differentials between entering, incumbents, and dying plants, and across birth cohorts with the purpose of shedding light at the role of entrants in industry productivity. The goal is therefore to determine if productivity differentials reveal turnover patterns. The working panel, as mentioned, has a total of 623 petrochemical plants distributed between plastics and synthetic resins. The older plant in the panel started operations in 1933 and the younger ones did in 1995. Because we are working with continuous information since 1974 it was necessary to classify plants according to birth cohorts by five-year periods to simplify the analysis.

Annex1 draws the map of industrial plants based on the five-year period, entry cohort and transition status. There are five working cohorts from 1975 to 1998. The chart flow has five layers indicating what the plant cohorts are. Plants might belong to cohorts a, b, c, d, and z. Each cohort has assigned a subscript of five-year period. Thus plants belonging to the first cohort (a) are those plants founded before 1979. They split in two groups. The surviving plants that report data for the next period, and the dying plants that exit the market during the period. They are marked with the superscript S and X respectively. The second layer indicates the plants that were born between 1980 and 1984. Thus the staked data in the panel within this period have records from plants from the first and second cohorts (a and b). Again plants might survive or exit the market regardless their cohort. Surviving plants from the cohorts (a) and (b) will have records in the next period [1985-1989]. At the same time new plants enter in the market within the period and are grouped as cohort (c). The reading of the entry and exit flows continues in the same manner up to the last cohort/period, which has plants from all five cohorts.

Testing productivity differentials lead to contrasting differences in total factor productivity and labor productivity based on the above-mentioned structure of plant cohorts and entry status. Firm selection theory [Jovanovic (1982), Audretsch (1995)] predicts that entrants are more productive than incumbents and they catch-up minimal efficiency scales to industry benchmarks. Thus, TFP levels in the short-run must be higher for entrants and these are the hypotheses behind the structure of Annex 1. We carried out three exercises. The first one contrasted productivity between surviving and exiting plants that belong to the same birth-cohort by means of testing changes in means and medians. These tests depict the direction that a firm performance variable such as productivity takes within a given sample. The test on medians evaluates proxy distribution shape through the non-parametric Wilcoxon rank-sum test.

Table 5. Productivity level differentials between exiting and surviving plants by cohort Pearson and Wilcoxon Rank-Sum Tests

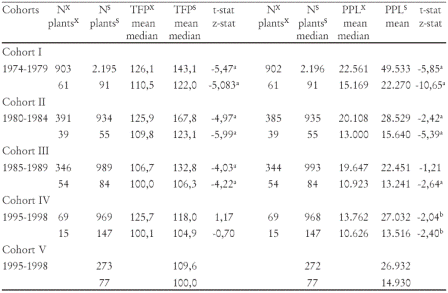
Notes: X= exiting plants; S=surviving plants. TFP is the translog index of TFP where entry date = 100, PPL = PPL= VA/L, in thousand of pesos at 1998 prices per worker per year. N= Number of observations are firm-year observations. The panel is an unbalanced time series-cross section dataset. Plants= Number of plants or individuals within the panel by cohort and entry dynamics; DUM1= dummy variable to test changes in average TFP and labor productivity between exiting and surviving plants by cohort. The variable takes the value of 1 if marked as an exiting plant. They are former incumbents for the first cohort or entrants for successor cohorts. Surviving firms are plants, which are successful entrants or incumbents. Incumbents in the study are defined as reporting plants for the 1974-1998 period. a= statistically significant at 0.01; b= statistically significant at 0.05; c= statistically significant at 0.1

Source: Own estimations based on DANE-EAM

Methodology: t-tests = Ho: mean(x)-mean(s) = difference = 0; z-test = Ho: median(x) = median(s)

Table 5 summarizes the results of this exercise. The sample size (N) is equal to plant-year observations according to birth cohort. Incumbents are individuals that report for the entire period, entrants are successful births for any given period that are still active by 1998, and exiting plants are those that shut down operations within a given period. Thus, incumbents and entrants in this context form the surviving plants.¹³ Differences in total productivity levels given by the TFP translog indices are statistically significant at 1 percent level for the first three cohorts. The mean (median) difference between surviving and exiting plants is 17 (11.5) points for cohort I, 42 (13.2) points for cohort II, and 26 (6.3) for cohort III. In contrast, for cohort IV we cannot reject the hypothesis of no productivity differentials. The outcomes for labor productivity are robust and go in the same direction. On average labor productivity is higher in surviving plants but the difference tends to close over time. For instance the mean (median) is $26.9 ($7.1) millions per worker/year for cohort I, $8.4 ($2.6) millions for cohort II, and $2.8 ($2.3) millions for cohort III. The mean labor productivity differential for cohort IV raises but not its median, which remains almost constant ($2.9 millions)¹⁴. The differences are significant at 5% level.

The second implication of the firm selection model further restricts the test on productivity differentials. In particular, if surviving firms are in fact more efficient over time, is there a difference between incumbents and successful entrants? TFP growth showed a long run rate of 5% per year for entrants and 1.9% per year for incumbent plants. From the perspective of entry flows they indicate that a successful entrant at time t becomes an incumbent firm at time t+1. Then with time passing older entrants' productivity first catch up with industry benchmarks and then turn into newly incumbents. This process characterizes the formation of generations of entrepreneurs. In the case of petrochemicals in Colombia it is clear that the industry entry patterns indicate that at least two generations of entrepreneurs were created. The older incumbents that started up from the 1950s to the 1970s and the successful entrants after 1980 located mainly within the plastic industry.

Table 6 presents the results of testing productivity differentials between entrants and incumbents plants by cohort that takes into account entry dynamics where entrants at period t, turn out incumbents at period t+1. The sample size (N) consists of plant-year observations where the maximum number of records for each plant within a given cohort/period, are 5 observations, where the number of incumbents increases over time. It began with 78 plants for cohort I, and ends up with 377 plants in the last cohort. Three results are worth mentioning. First, productivity levels given by the average value across plants of the TFP translog indices follow a concave function reaching a local maximum with an index value of 154 during the 1990-1994 period.

This means that TFP in surviving plants grows faster during their first years of operations and then slows down. New firms shift out industry TFP levels but the productivity growth exhibits decreasing rates because of productivity decreases with entrants' ageing. Second, total factor or labor productivity differences between new-births and incumbents become significant after the effect of firm entry of the first cohorts takes place on overall industry productivity. That is, entry penetration induces productive plants to lead industry productivity and to generate a reallocation effect toward younger firms in the industry. The result also suggests that there is an initial disadvantage in scale efficiencies of new plants with respect to incumbents. They are smaller plants that cannot exploit internal economies of scale. The above differences are significant at 5% level. Third, the hypothesis of no entry differentials is consistently rejected across cohorts at 1% level.

The above results prove that plant heterogeneity explains the existence of productivity differentials across plant cohorts meaning that there are important plant turnovers. Therefore we performed a third exercise in testing productivity differentials and focusing on the role of turnovers of industry productivity in order to figure out the size and importance of the reallocation effects of fixed factors toward more productive plants.

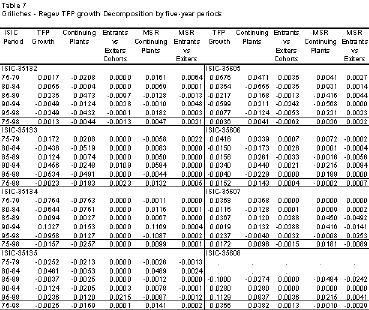
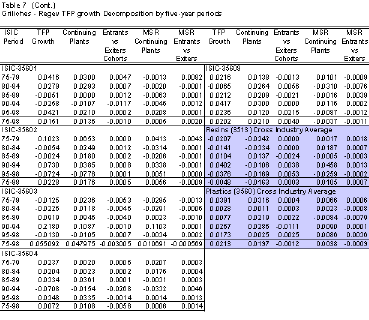
The measurement was done for the 13 five-digit ISIC-groups within petrochemicals that belong to resins and plastic industries. Table 7 reports the results of technical change decomposition exercise following Griliches-Regev methodology given by equation 5. This decomposition captures the contribution of continuing plants, the net entry effect and market share reallocation into the TFP growth rates. Each component is reported in the last four columns in the table. Several are the results worth mentioning. First, productivity of continuing firms is the main source of TFP growth across petrochemical markets. Their contribution is in both directions. Improvements in incumbent's efficiency will reflect gains in overall industry productivity as well as productivity deterioration will end up in industry's efficiency losses. The former is the case for plastics and its products, while the latter describes the case of synthetic resins.

Table 6. Productivity Level Differentials Between Incumbent and Entering Plants by Cohort and Year Pearson, Wilcoxon Rank-Sum, and F-tests

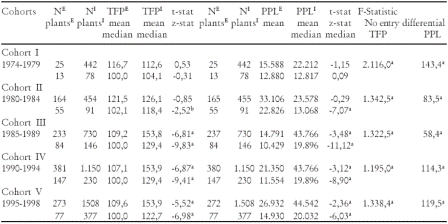
Notes: E= entrants; I=Incumbents; TFP = translog index of total factor productivity where entry date = 100, PPL = Labor partial-productivity expressed in thousand of pesos at 1998 prices per worker per year; N= Number of observations are firm-year observations. The panel is an unbalanced time series-cross section dataset; Plants= Number of plants or individuals within the panel by cohort and entry dynamics. DUM2 = Dummy to test changes in means by cohort between successful entrants and incumbents by cohort. The dummy variable that takes the value of 1 if the plant is marked as an ENTRANT, 0 if is an INCUMBENT in the sample for the T-tests evaluations. Entrants t-1 = Incumbents t by five year period. The observations are 5 per plant. a= statistically significant at 0.01; b= statistically significant at 0.05; c= statistically significant at 0.1;

Source: Own estimations based on DANE-EAM

Methodology: T-tests = Ho: mean (E)-mean (I) = difference=0; z-test = Ho: median (E) = median (I); The F-test for testing overall productivity differentials across cohorts is defined through the following regression equation:

where: Y = TFP or PPL; Dummy1 = 1 if i is an entrant, zero otherwise; dummy2 = 1 if i is an incumbent, zero otherwise.

The null is:

The minimum contribution of continuing plants to the TFP growth industry within plastics was 55% located in the manufacture of plastic shoes ant their parts [ISIC 35607]. The other plastic industry-groups the contribution is greater than 87% of TFP growth. In most cases the sign of TFP growth rate of continuing firms matches to industry-specific productivity growth. In contrasts, productivity deterioration of incumbent plants shifted down productivity within the synthetic resins industry. Efficiency of continuing plants decreases in all four groups exhibiting long run negative growth rates.

The above results are consistent with other international studies of productivity that use similar decompositions. For instance, Aw, Cheng & Roberts (2001) report an average accumulated TFP growth rate for the plastic industry of 12% and 11.8% between census periods of 1981, 1986 and 1991. Continuing plants contribution were 7.1 and 8.0 percentage points respectively. That is an average contribution of 63%. Liu & Tybout (1996) report technical efficiency decomposition between incumbent and turnover effect in five major ISIC 2-digits manufacturing groups for Colombia during the 1979-1986 period. The cross industry average of TFP growth across was 1.63% per year. Incumbents grew 1.49% and the remainder is due the turnover effect.¹⁵

Griliches & Regev (1995) report a labor productivity (LP) growth decomposition between the within effect (incumbents) and the mobility effect (market share reallocation) for the Israeli manufacturing by industry-specific 3 digits-ISIC codes for the 1979-1988 period. For instance, the average growth of LP for other chemical was 7.1%. The within effect accounted for 6.8% percentage points out the total growth.¹⁶

Balwing & Gu (2002) present an analysis of labor productivity growth decomposition for Canadian manufacturing following Griliches-Regev (1995) approach. They report an average labor productivity growth and its components for two periods: 1979-1988 and 1988-1997. Average LP growth and the within-plant effect in each of these periods were: 1.16% (1.10%), 1.13% (1.09%) for plastics, and 2.41(1.40%), and 2.74% (2.59%) for the chemical industry. Baily, Hulten & Campbell (1992) undertook a complete analysis of productivity dynamics at plant level for 23 US industries based on five manufacturing census years (1972, 1977, 1982, 1987). They broke TFP growth as the sum of continuing plants, output reallocation across incumbents and net entry (turnover). They found for instance that for all industries the growth of TFP and the incumbent effects between censuses were: 7.17% (5.04%), 2.39 (-1.09), and 15.63% (13.52%) respectively.¹⁷

Second, market share reallocation across continuing plants constitutes an important source of productivity growth. This outcome implies that there was an effective substitution of resources toward more productive plants across petrochemical-groups. This source was more dynamic within synthetic resins in contrast to plastics subgroups. The long run growth rate was 1.1% within resins and 0.4% within plastics per year. This finding is important because in the former case TFP growth across subgroups had a negative rate of -0.48% per year for the entire period of 1975-1998. In this case productivity deterioration would have been greater if there were not such increase in market share of the more productive plants.

Table 7. Griliches - Regev TFP Growth Decomposition by Five-year Periods

Source: Own estimations base on Dane-EAM

Methodology: Griliches-Regev (1995) productivity decomposition

Third, the contribution of the turnover effect to TFP growth is low across petrochemical groups. The growth rate differentials in productivity between entering and exiting plants across periods/groups range from -0.09% (2.1%) in resins and -3.8%(2.8%) in plastics. This outcome reflects two facts. On one hand, there are not significant productivity differentials between entry and exiting plants. The result is consistent with the results of section 4.2; entrants (exiters) tend to have less scale economies than incumbents. Once entrants become incumbents or survive as time passes they do a catching up with industry's productivity benchmarks. The result in the plastic industry for instance was that successful entrants shaped plant minimal efficient scales as well as total productivity. Nonetheless, this happened once entrants matured and became new established firms. In other words, productivity improvements that occurred following entry showed up as productivity improvements of the continuing plants.¹⁸ This result also reflects the low entry penetration rate documented in the first section. It is a common fact that entrants for any given year have a low market share with respect to the incumbent plants.

On the other hand, differences in market shares between entrants and exiters is also negligible, therefore their contribution to TFP growth is too low in most petrochemical groups. The cross industry average for the entire period of this component is 0.07% in resins, and in plastics is -0.09% per year. Despite the above, the turnover effect is important across subgroups for specific periods. There are 10 out of 43 periods were the negative rates of TFP growth were partially offset by positive changes in turnovers within the plastic industry. For instance, productivity growth in the manufacture of plastic shoes industry group [ISIC 35607] was 2.37% for the 1995-1998 period. The differential in market shares explained 2.53% points for that period.

Summarizing, the effect of output reallocation to enhance total factor productivity levels and growth in petrochemicals was low for the analyzed period. This is a consequence of low entry penetration rates. The share of entrants into industry output was less than 10% for all sub-groups excepting in ISIC-35135 [Table 3]. Nonetheless, the measurement of the TFP translog indices showed a substantial difference in productivity levels and growth rates between incumbents and successful entrants as a whole. Plants that were born after 1977 shaped industry productivity levels by the 1980s and 1990s but once they became incumbents the output share of new plants did not steadily increase over time to boost penetration rates. The next section presents the econometric analysis of entry rates determinants in the petrochemical industry as a function of entry barriers and market incentives to entry.

IV. The Econometrics of Entry Rates

The general model used in this work to explain the determinants of plant entry in the petrochemical industry is borrowed from Orr's seminal paper. That approach has been extensively employed in international research on determinants of entry.¹⁹. Following Khemani & Shapiro (1986), the entry equation is given by

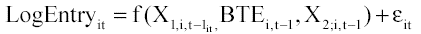(6)

where: Log Entry is the gross number of plants that entered each petrochemical group between 1975 and 1998.

However, we do not do not observe the type of entry due to new startups, new plant acquisitions, or mergers. Following Mata (1993) and Roberts & Thompson (2003), we add one to the number of (gross) entrants before doing the logarithmic transformation.²⁰ X1 is a vector of variables that controls for incentives to enter, BTE stands for those variables that are barriers to entry, and X2 is a vector of complementary variables that have been found to be important in explaining entry in international studies. Again all variables are at 12 ISIC specific petrochemical groups for the 1975-1998 period.²¹ Further variable definitions and their expected signs are shown in Annex 6.

The vector of X1 regressors is composed mainly by two variables, commonly used in the literature. The first one is the annual growth of the price-cost margin (gPCM) of industry lagged one period. It proxies observed profitability, and as Orr (1974) stated, it reflects the extent to which economic rents have been captured by existing firms. The second variable is the market room (MROOM). It captures the effect that entry is more likely to occur whenever there have been industry growth. We follow the definition of Rosenbaum & Lamort (1992). The BTE-vector is composed of some variables used in Orr-type models and one should expect all of them to be negatively related to entry. The first one is advertising intensity. It is measured as the ratio of the spending in advertising to value added. The second barrier to entry variable is a proxy for technology. It is defined as the ratio of expenses of royalties paid by firms in industry i to the value added of that industry (ROY). BTE variables that are determined by structural characteristics were also included. The first one is called Scale, and proxies the extent of economies of scales in industry i. It is a composed variable defined as the ratio of minimum efficient scale over the cost-disadvantage ratio. A second structural variable is the log of the capital-to-output ratio (Log KOR). The last variable is the dependence of imported raw material (DMRM). This proxy is included because the domestic petrochemical industry has been heavily dependent on imported raw material despite the fact they were thought to be substituting petrochemical inputs. It is not a variable included in any of the studies reported in Annex 5, and since the access and the associated costs of imported inputs have been commonly difficult, one should expect it to be negatively correlated with entry.

The X2 vector is formed mainly by idiosyncratic variables as well as other variables found relevant in the mainstream literature. The first idiosyncratic is the building and construction GDP growth (GROCONS). The two 4-digit petrochemical industries represent the upstream and downstream links of a branch of petrochemicals. Their main user of those (final) goods has been the Colombian building and construction industry. Then, one should expect that as the rate of growth of building increases, so does entry and vice versa. The second variable included in this set is the translog indices of total factor productivity (TFP), which captures industry weighted average productivity levels. Although not idiosyncratic to petrochemicals, it is a variable that has not been employed previously in any of the studies above reported. The insight with TFP indices is that industries with better total factor productivity are those where inefficient firms are very likely to drop the market and then open room to new entrants.

Three additional variables are the proxy for risk, an industry concentration index, and a measure of the fringe in each industry i. For the first one, we employ the standard deviation of the price-cost-margin (RISK), the second the Herfindal concentration index (HH), and the last one is fringe competition (FRINGE) that is constructed following the methodology of Rosenbaum & Lamort (1992): the percentage of firms with fewer than 50 employees. This variable is meant to capture the relative size of the fringe in an industry and it is expected that the larger the fringe the higher the entry. Last, since the study by Shapiro & Khemani (1987), it has been acknowledged that the displacement effect (or the effect that new entry generates exit and vice versa) must be included in the determinants of entry. In that direction, recently, Roberts & Thompson (2003) introduced both past exit (NXt-1) and past entry (NEt-2) into the determinants of entry. The rationale is that past exit open room while past entry could "capture some omitted height of entry barriers effect". Therefore, the expected sign of those variables is positive. All the variables were lagged one period.

The studies listed in Annex 5 show that regressions follow standard specifications. Most of the studies just run OLS, and since they had information about the whole manufacturing industries, some do pooled cross-section and time series, others rely on to 2SLS, and the rest employ FGLS and panel data. We run the above specifications, due to the working panel is an unbalanced matrix of 12 petrochemical industries (individuals) with time span for about 24 years (within observations). Tobit regressions were included because the dependent variable is censored at value of cero. Annex 7 reports the variables main statistics and Annex 8 shows their correlation matrix.

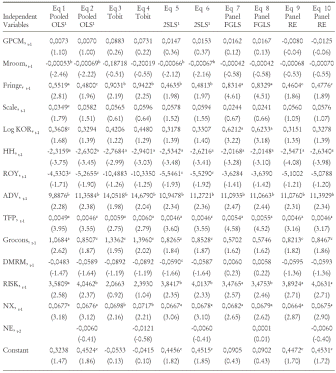
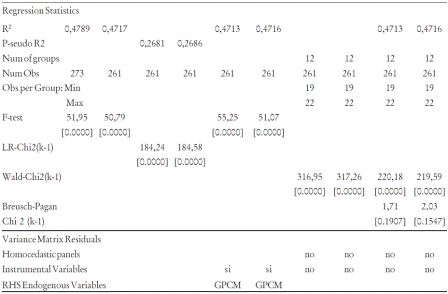
Table 8 reports the main findings about the determinants of entry in Colombian petrochemical industries. There, the reader can notice the five different econometric specifications we ran. For each of them there appear two equations. The only difference is the inclusion of gross entry lagged two periods and the exit variable to account for the potential room that exits open to new entrants. The results running OLS, Tobit, 2SLS and FGLS are very similar and with an acceptable global significance of the model and goodness of fit. On average the model explains 47% of gross entry flows. The panel data random effect model gets similar results but the Breusch-Pagan test clearly rejects the hypothesis of that specification.

The first striking result is the fact that regardless of the econometric specification both the lagged growth in price margin and market room, proxy of industry i dynamics, were found either not to be significant in the first case, (although with the right expected sign), or significant some times but with the wrong sign in the second one. Although at odds with the theoretical arguments, the no significance of profit cost margin was also found in Orr's paper and others. Second, BTE barriers show mixed results. Neither scale (SCALE) nor the log of capital-to-output ratio (LOG KOR) were significant, and all cases with the opposite sign. The result could be explained by the real development in plastics took place since the 1980s where entry occurred and plant scale were low. The licensing indicator (ROY) turned out a robust entry barrier. If continuer firms invest in leasing patented technologies it constitutes a fix cost that will deter entry. On average, if incumbents increase 1% their licensing spending entry flows will fall in around 5%.

Advertising intensity (ADV) is also a robust regressor although it exhibits a positive relationship with entry. The variable was significant under all the econometric specifications. From theory, advertising intensity is expected to be a barrier to entry if it just conveys a persuasive goal. In that case, expenses in advertising create a barrier to entry since new potential entrants must waste huge amount of money to gain (small) market participation.

What can then explain the positive relationship? Some studies have found also a positive correlation between entry and advertising. Among them, Telser (1962), Hirschey (1981) and MacDonald (1986) present evidence that advertising may facilitate entry and new product innovations. The theory behind this explanation may be borrowed from Schmalensee (1978) who presents some arguments about the positive relationship between profitability and entry. Advertising plays an informative role and when incumbent firms advertise, they create or strengthen market demand. Then the existence of such spillovers makes entry ease firm entry. However, it is expected that advertising has a role only for consumer goods and lesser degree for intermediate goods. Plastic products satisfy that condition since most of them manufacture "in some way consumer goods. Last, the dependence of imported raw materials ratio (DMRM) is significant and with the right sign for 2SLS without the exit variable and has the expected sign for most of the regressions but not statistically significant. Despite that it shows that when studying entry researchers should pay attention to variables like the dependence of raw material that in certain specific situations may be relevant.

Third, regarding the complementary variables, the Herfindal concentration ratio is significant in all regression equations with the expected negative relationship. On average, an increase in 1% in the market concentration entry drops in 2.5%. Hence, industry concentration deters entry. Productivity levels (TFP) turn out a robust determinant with the expected sign. As long as productivity raises due to market reallocation effects will induce entry. On average, the regression coefficients indicate that an increase in 10 points on TFP indices entry will increase in 0.46%.

The annual growth rate of the building and construction GDP (GROCON) also turn out a significant regressor. This variable captures the macro effect that tends to facilitate entry. Only in a couple of regressions, it falls short of getting the ten per cent significance. As in the paper by Orr and others, one proxy for risk is included in the estimations. Under the assumption that the greater the risk firm could face, the lower the incentives to enter and then the lower would be entry. However, almost all the equations show a positive and significant relationship between the measure of risk (the standard deviation of the PCM) and the level of entry. Recently, Roberts and Thompson (2003) also found a similar positive association. They conjecture here is that if one considers the variability of past profitability as "a measure of intra-industry heterogeneity, hence an indicator of the potential for niche entry, the significant positive coefficient appears sensible" [(Roberts & Thompson 2003, p 241, italics added].

That interpretation is more sensible if one notices that fringe competition that controls for how small firms are represented in the industry is always positive and significant. On average, as the competitive fringe raises 1% entry will boost in 0.65%. This result is consistent with the fact that entry in plastics is formed by medium-size plants with an average less 50 employees since the 1985.

Finally, the regressions include the test of whether the displacement effect has any effect on the level of entry and if past entry could deter or facilitate entry. The past exit variable XN, is in all equations significant averaging a positive effect of 6% on entry if the exit rate increases in 10%. Thus, plant exit induce entry through increments in market room. Past entry (NEt-2) exhibits the correct sign although this variable is not statistically significant in the regression equations.

Summing up, the determinants of entry have been tested for developed economies and more recently for transition economies. Some general specifications borrowed from Orr's model have been used and tested, and the main variables employed to explain entry are commonly known. In this paper based on that research, we tested the determinants of entry for an industry case in a developing economy. The appealing of the above-explained results is that the basic Orr-type model holds for this case study as predicted in theory, and with the previous findings in the international literature on firm entry.

Table 8. Regression Analysis. Pooled, GLS, Random Effects and Tobit Estimations. Dependent Variable: Log of Gross Entry

V. Conclusions

This paper has conducted an in-depth study of plant entry within the petrochemical industry in Colombia. The importance of this study within an international context is that there are few case studies on specific industries and entry dynamics for developing economies that cover long-run trends and, more importantly, within formerly protected industries that were set up during the import substituting industrialization phases. As was the case in other Latin American countries, the Colombian petrochemical industry was seen as a strategic industry to promote and deepen domestic industrialization five decades ago.

This study shows that entry was a common regularity during the analyzed period, which covered the mixed strategy of import protection and export promotion of the 1970s and 1980s, as well as the economic liberalization strategy of the 1990s. Gross entry in the industry was located in the plastics industry and to a much lesser extent within synthetic-chemical resins, in spite of the trade regime. Moreover, plant entry accelerated since the mid-1980s and in the plastics industry during the 1990s. Despite the above our survival estimates show that 50 percent of total entrants die within the first 7 years. This finding is consistent to Geroski's stylized facts of low survival rates. One reason that explains such fact is that the plastic industry is formed by medium-size plants.

Productivity differentials were a constant regularity between surviving and exiting plants, as well as incumbents versus entrants. Successful entrants shaped industry productivity. Total factor productivity measures showed that this group of firms/plants had 2.1 times the average productivity level of old firms, which started commercial operations before 1977. At the same time, employment generation was upheld in this group within petrochemicals. TFP growth decomposition showed that the incumbent effect dominates the turnover effect. Total factor productivity growth decomposition showed that the continuing plants productivity drives industry efficiency. There was also an important contribution to productivity growth due to market reallocation toward more productive plants across incumbents and surviving entrants.

On the other hand there were not large differential between entering and exiting plants as well as differences in market shares. Thus, the turnover effect between entrants and dying firms was low in the 13 studied petrochemical branches. This result is correlated with the low penetration rates on entering plants within any given year, which in turn is a common result according to the evidence reported by entry studies for OECD economies.

The econometric exercise corroborates that the Orr-type model explains in certain degree the entry rates within petrochemicals. The regression results are mixed. On one hand, the pure incentive to market variables turn out no significant variables in the regressions. Barriers to entry played important role in deter entry through technology licensing, market concentration, and dependence from imported materials. Surprisingly the advertising indicator showed the opposite sign. This result has been found in other studies. The complementary variables turned out robust determinants. Increases in industry TFP and GDP growth in housing construction boost entry. The risk proxy reported the opposite sign in accordance with findings in recent studies of firm entry. There is a spillover that potential entrants foresee new market niches because the existence of firm/industry heterogeneity. Last, plant exit induces ex-post entry meaning that the replacement effect holds in the model.

Annex

Annex 9 - The Annual Manufacturing Survey: An overview The Annual Manufacturing Survey of Colombia [Encuesta Anual Manufacturera (EAM)] is in practice a census of medium and large enterprises in manufacturing. The EAM has undergone three methodological changes affecting the following time periods, respectively: i) 1970-1991, ii) 1992-1993, and iii) 1994 to date. The changes have been addressed toward: i) the inclusion or exclusion of variables within chapters; ii) the addition or suppression of new information across chapters; iii) modification of the format or variable classification criteria; and iv) the rescaling of the sample cohorts.

Some specific examples are the changes of the payroll classification, the inclusion of temporary workers after 1987, the exclusion of direct exports as a component of firm's sales, the elimination of the direct tax variables after 1991, the redefinition of large enterprise according to number employees, and the addition of new components for fixed investment after 1992, among many others.

Despite the format modifications, the survey has kept the basic variables and structure across time. The database clean up process was a two-step procedure. First, we worked with the basic variables of the 1970-1991 survey. Second, all basic series were overlapped and grouped keeping the original definitions of the older survey. The manufacturing survey offers five types of variables:

1. Identification variables: Location (blue-park district), specific ISIC group, firm's legal capital structure, and size classification. 2. Labor variables: Wages, benefits, permanent and temporary employees, administrative employees, workers, technicians, and gender statistics. 3. Output-related variables: Gross output, value added, intermediate consumption components, industrial expenditures, and inventories of final products and raw materials. 4. Finance-related variables: Fixed asset investment, accounting depreciation, sales, marketing spending, paid royalties, and other general expenditure variables. 5. Consumption, generation, and sales of electricity.

The survey recorded data for 133 variables from 1970 to 1991. The survey recorded 380 variables during 1992 and 1993. From 1994 to date, the survey has worked with 200 variables. The 1992-1993 period is problematic because the survey included information that was not comparable with previous data. However, the core variables were recorded.

Notes

1 Annex 9 presents an overview of the EAM structure explaining what the main limitations and advantages are.

2 Annex 2 depicts the petrochemical tree. Annex 3 lists the names of each of these 13 manufacturing groups located within synthetic resins and the plastic industries.

3 According to Geroski (1995) gross entry in the US Chemical industry were 322 new firms.

4 Complementary information concerning survival by cohorts is in Annex 5.

5 Two caveats are important to have in mind. Since we ruled out for the analysis all firms that did not report information for at least four years, many small starts-up that fell into that classification actually could have survived and so the survival indicator may be understated. Second, the percentage of firms surviving more than fifteen years may be understated given the changes in the ID code number and the high gross exit that occurred in 1991 and 1992.

6 See for details 5

7 The plants in the panel fulfill the following requirements in order of not being classified as volatile plants: i) plants most have at least 4 consecutive observations within the 1974-1998 period in their main variables excepting gross investment; and ii) plant basic series must be continuous or exhibit a discontinuity for a maximum of three (3) years. In these cases, we perform an interpolation across observations. The difference between the unbalanced panel with the 623 plants and the one used in section II is explained by the inclusion of plants that do report for the 1997-1998 period and for the productivity panel they do not fulfill condition i). This avoids truncation in entry rates series. The above implies a difference of 150 plants between the two panels.

8 The observed changes in factor shares are also explained by changes in factor prices that are not related to changes in input marginal productivities, but with distortions and rigidities in the labor and capital markets. Therefore, the observed productivity growth rates might be neutral or not.

9 For details on the properties of exact indices and flexible functional forms see the original work of Diewert (1976). Regarding the derivation of the transcendental logarithmic production function see Christensen et al (1971). A comprehensive application of index numbers in measuring TFP growth across Colombian manufacturing sectors, see Pombo (1999a).

10 For more details in the application of this methodology to the EAM dataset, see Pombo op cit. (1999a).

11 On this particular, productivity studies at firm or industry levels have introduced market failures and measured TFP through the inclusion of markups and imperfect competition (Hall (1988)), output scale (Nadiri & Schankerman (1981)), rate of return of regulation (Denny, Fuss, & Waverman (1981)), factor demand endogeneity and quasi-fixed inputs (Morrison (1986, 1988, 1992)), rate of installed capacity utilization (Fuss & Berndt (1986)). Pombo (1999b) presents an application for Colombia in measuring TFP indices in manufacturing, introducing imperfect competition through markups and variable returns to scale.

12 We follow the notation used in the study of Aw, Cheng and Roberts (2001).

13 For instance, the table report 2195 plants for cohort I. Among them there are plants founded since 1933 up to 1979. Plants founded in 1978 or 1979 that are still reporting by 1998 are the entrants of this cohort. Plants that reported on or before 1977 to 1998 are the incumbents. Exiting plants are the units that failed within the 1974-1979 period. Recall that in all cases the first observation is 1974. The total surviving plants for this cohort are 91 while dying plants are 61.

14 Notice that there is not exiting plants for cohort V. This is a result of the truncation derived from the conditions imposed to all units in the final-panel in order of not being classified as a volatile plant.

15 The manufacturing sectors included in Liu and Tybout (1996) study for Colombia were: Food (0.63%; 0.60%), Textiles (6.4%; 6.5%), Footwear (2.1%; 1.7%), Wood Products (-0.14%; -0.30%), Metal Products (-0.92%, -1.01%). Numbers in parenthesis indicate the average industry-specific TFP growth rate and continuing plants TFP growth rate for the whole period. For more details see table 4.2.

16 Average labor productivity growth and the within effect were 0.04% (-1%) for plastics, and 5.3% (4.5%) for basic chemicals for the same period (figure 5, pp. 185). It is implicit that other chemicals include the petrochemical branches excepting plastics.

17 The only chemical subgroup included in this study was inorganic or basic chemicals that include the manufacture of acids, urea, sulfates, etc. TFP growth and incumbents' TFP growth across censuses were: 5.7% (1.28%), -13.24% (-19.96%), and 10.57% (7.75%).

18 These results mirror previous ones that use annual data such as the studies for Israel, Canada, Chile and Colombia. Inter-census studies also confirm that the incumbent effect dominates the turnover effect. The exception is the study for Taiwan where productivity differentials between entrants and exiters constitute and important source of TFP growth. For instance, Aw et al. (2001) report for the Taiwanese chemical industry an accumulated TFP growth of 11.9% among censuses. Productivity differentials account for 3.85% out of this total.

19 Annex 5 lists the most relevant empirical studies on firm entry since Orr's 1974 paper.

20 A total of 120 cases of no entry were recorded during the period under study.

21 The number of ISIC-five-digits industries is 12 since ISIC 35608 was excluded from the sample. The main reason is that the number of plants in this plastic-subgroup is extremely low (three) and in fact is an outlier. In addition, times series start after 1987.

22 The main problem of the above methodological changes was the modification in the basic plant ID variable from 1991 to 1992, and 1993. This is troublesome if one wants to track the information at plant level. We ran a cross matching program throughout plant commercial names, recorded at the industrial directories, and generated an identification key for the ID variables in the 1991-1992 and 1992-1993 surveys.

References

1. Audretsch, David, 1995, Innovation and Industry Evolution. The MIT Press, Cambridge, Massachusetts.        [ Links ]

2. Aw, Bee Jan; Chen, Xiaoming and Roberts, Mark, 2001, "Firm-Level evidence on productivity differentials and turnover in Taiwanese manufacturing", Journal of Development Economics, No. 66, pp.51-66.        [ Links ]

3. Baldwin, John R., 1995, The Dynamics of Industrial Competition: A North American Perspective, Cambridge University Press, Cambridge, U.K.        [ Links ]

4. Baldwin, John R., Beckstead, Desmond and Girard, Andrée, 2002, "The Importance of Entry to Canadian Manufacturing", STI Working Paper 2002/03, OECD, Paris.        [ Links ]

5. Baldwin, John R. and Gu, Wulong, 2002 "Plant Turnover and Productivity Growth in Canadian Manufacturing", STI Working Paper 2002/03, OECD, Paris.        [ Links ]

6. Cable, John and Schwalbach, Joachim, 1991, "International Comparisons of Entry and Exit". In Geroski, P. A. and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell, Oxford, UK.        [ Links ]

7. Caves, Richard, 1998, "Industrial Organization and New Findings on the Turnover and Mobility of Firms", Journal of Economic Literature, No. 36, pp. 1947-1982.        [ Links ]

8. Christensen, Lauris; Jorgenson, Dale and Lau, Lawrence, 1971, "Conjugate duality and the transcendental logarithmic function", Econometrica, No. 39, pp. 255-256.        [ Links ]

9. Denny, Michael; Fuss, Melvyn M. and Waverman, Leonard, 1981, "The measurement and interpretation of total factor productivity in the regulated industries, with an application to Canadian telecommunications". In: Cowing, T. and Stevenson, R. (eds.), Productivity Measurement in Regulated Industries, New York, Academic Press.        [ Links ]

10. Diewert, Erwin W., 1976, "Exact and superlative index numbers", Journal of Econometrics, No. 4, pp. 115-145.        [ Links ]

11. Disney, Richard., Jonathan Haskel, and Ylva Heden, 2003 "Entry, Exit and Establishment Survival in UK Manufacturing", The Journal of Industrial Economics, 51: 91-112.        [ Links ]

12. Geroski, Paul, 1988, "Patterns of Firm Entry and Exit in the U.S. Manufacturing Industries", Rand Journal of Economics, No.19, pp. 495-515.        [ Links ]

13. Geroski, Paul and Roberts, Mark, 1991, "Variation in Producer Turnover across US Manufacturing Industries". In: Geroski, P. A and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell, Oxford, U.K.        [ Links ]

14. Evans, Laurie B. and Siegfried, John, 1992 "Entry and Exit in United States Manufacturing Industries from 1977 to 1982". In Audretsch, D. B. and Siegfried, J. J. (eds.), Empirical Studies in Industrial Organization: Essays in Honor of Leonard Weiss, Kluwer Academic Publishers, Netherlands.        [ Links ]

15. Foster, Lucia; Haltiwanger, John and Krizan, C. J., 2001, "Aggregate Productivity Growth: Lessons from Microeconomics evidence". In: Dean, E.; Harper, M. and Hulten, C. (eds.) New Directions in Productivity Analysis, University of Chicago Press        [ Links ]

16. Geroski, Paul, 1991, Market Dynamics and Entry, Blackwell: Oxford, U.K.        [ Links ]

17. Geroski, Paul, and Mason, R. T., 1987, "Dynamic Market Models in Industrial Organization", International Journal of Industrial Organization, No. 5, pp. 1-13.        [ Links ]

18. Geroski, Paul, and Schwalbach, J., 1991, Entry and Market Constestability: An International Comparison, Blackwell, Oxford, U.K.        [ Links ]

19. Geroski, Paul, 1995, "What do we know about Entry?" International Journal of Industrial Organization, No. 32, pp. 421-440.        [ Links ]

20. Griliches, Zvi and Regev, Haim, 1995, "Firm Productivity in Israeli Industry: 1979-1989", Journal of Econometrics, No. 65, pp. 175-203.        [ Links ]

21. Hall, Robert, 1988, "The relation between price and marginal cost in US industry", Journal of Political Economy, No. 96, pp. 921-947.        [ Links ]

22. Hirschey, Mark, 1981, "The effect of advertising in the industry mobility", Journal of Business, No. 54, pp. 329-339.        [ Links ]

23. Kap Young, Jeong and Masson, Robert T., 1991, "Entry during Explosive Growth: Korea during Take-Off". In: Geroski, P. A and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell: Oxford, U.K.        [ Links ]

24. Jorgenson, Dale and Griliches, Zvi, 1967, "The explanation of productivity change", Review of Economic Studies, No. 34, pp. 249-283.        [ Links ]

25. Jovanovic, Boyan, 1982, "Selection and Evolution of Industry", Econometrica, No. 50, pp. 649-670.        [ Links ]

26. Khemani, Shyam and Shapiro, Daniel, 1986, "The Determinants of New Plant Entry in Canada", Applied Economics, No. 18, pp. 1243-1257.        [ Links ]

27. Levinsohn, James and Petrin, Amil, 2003, "Estimating Production Functions Using Inputs to Control for Unobservables", Review of Economic Studies, No. 70, pp. 317-341.        [ Links ]

28. Liu, Lili and Tybout, James, 1996, "Productivity Growth in Colombia and Chile: Panel-based evidence on the role of entry, exit, and learning". In: Roberts, M. and Tybout, Eds, Industrial Evolution in Developing Countries, The World Bank-Oxford University Press, Washington.        [ Links ]

29. MacDonald, James, 1986, "Entry and exit on the competitive fringe", Southern Economic Journal, No. 52, pp. 640-652.        [ Links ]

30. Mata, José, 1991, "Sunk Costs and Entry by Small and Large Plants". In: Geroski, A. P. and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell, Oxford, U.K.        [ Links ]

31. Mata, José, 1993 "Entry and Type of Entrant: Evidence from Portugal", International Journal of Industrial Organization, No. 11, pp. 101-122.        [ Links ]

32. Mata, José, Portugal, Pedro and Guimaraes, Paulo, 1995, "The Survival of new Plant: Start-up Conditions and post-entry Evolution", International Journal of Industrial Organization, No. 32, pp. 459-481.        [ Links ]

33. Melendez, Marcela; Seim, Katja and Medina, Pablo, 2003, "Productivity Dynamics of the Colombian Manufacturing Sector", Documentos CEDE, No. 23, Universidad de los Andes.         [ Links ]

34. Morrison, Catherine, 1986, "Productivity measurement with non-static expectations and varying capacity utilization: An integrated approach", Journal of Econometrics, No. 33, pp. 51-74.        [ Links ]

35. Morrison, Catherine, 1988, "Quasi-fixed inputs in United States and Japanese manufacturing: A generalized Leontief cost function approach", Review of Economics and Statistics, No. 70, pp. 275-287.        [ Links ]

36. Morrison, Catherine, 1992b, "Unraveling the productivity growth slowdown in the United States, Canada, and Japan: The effects of sub-equilibrium, scale economies and markups", Review of Economics and Statistics, No. 74, pp. 381-393.        [ Links ]

37. Mueller, Dennis, 1991, "Entry, Exit, and the Competitive Process". In: Geroski, P. A and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell, Oxford, U.K.        [ Links ]

38. Nadiri, Ishaq and Schankerman, Mark, 1981, "The structure of production, technological change and rate of growth of total factor productivity in the US Bell System". In: Cowing, T. and Stevenson, R., Productivity Measurement in Regulated Industries, Academic Press, New York         [ Links ]

39. Olley, Steve and Pakes, Ariel, 1996, "The Dynamics of Productivity in the Telecommunication Industry", Econometrica, No. 64, pp. 1263-1297.        [ Links ]

40. Orr, Dale, 1974, "Determinants of Entry: A Study of the Canadian Manufacturing Industries", The Review of Economics and Statistics, No. 56, pp. 58-66.        [ Links ]

41. Pavcnik, Nina, 2002, "Trade Liberalization, Exit and Productivity Improvements: Evidence from Chile", The Review of Economic Studies, No. 69, pp. 245-276         [ Links ]

42. Pombo, Carlos, 1999a, "Productividad industrial en Colombia: Una aplicación de números índices", Revista de Economía del Rosario, junio.        [ Links ]

43. Pombo, Carlos, 1999b, "Economías de escala, markups, y determinantes del cambio técnico en la industria en Colombia", Coyuntura Económica, No. 29, pp. 107-132.        [ Links ]

44. Roberts, Barbara and Thompson, Steve, 2003, "Entry and Exit in a Transition Economy: The Case of Poland",Review of Industrial Organization, No. 22, pp. 225-243.        [ Links ]

45. Roberts, Mark and Tybout, James, 1996, Industrial Evolution in Developing Countries, The World Bank-Oxford University Press, Washington        [ Links ]

46. Rosenbaum, David and Lamort, Fabian, 1992, "Entry, Barriers, Exit, and Sunk Costs: an Analysis", Applied Economics, No. 24, pp. 297-304.        [ Links ]

47. Schmalensee, Richard, 1978, "A model of advertising and product quality", Journal of Political Economy, No. 83, pp. 485-503.        [ Links ]

48. Schwalbach, Joachim, 1991, "Entry, Exit, Concentration, and Market Contestability". In: Geroski, P. A and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell, Oxford, U.K.        [ Links ]

49. Shapiro, Daniel and Shyam Khemani, R., 1987, "The Determinants of Entry and Exit Reconsidered", International Journal of Industrial Organization, No. 5, pp. 15-26.        [ Links ]

50. Telser, Lester G., 1962, "Advertising and cigarettes" Journal of Political Economy, No. 70, pp. 471-99.        [ Links ]

51. Yamawaki, Hideki, 1991, "The Effects of Business Conditions on Net Entry: Evidence from Japan". In: Geroski, P. and Schwalbach, J. (eds.), Entry and Market Contestability: An International Comparison, Blackwell, Oxford, U.K.        [ Links ]