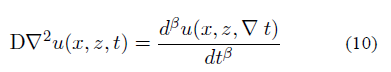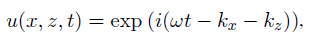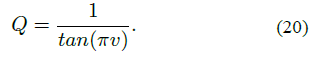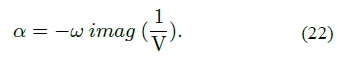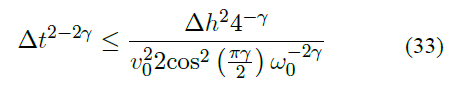Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
Introducción
Cuando una onda mecánica se propaga a través de un medio, sufre una disminución gradual de su amplitud, junto a su descomposición espectral en modos de propagación, donde cada modo se desplaza con su propia velocidad. Estos fenómenos se llaman atenuación y dispersión de ondas, respectivamente (Liner, 2004). Debido a las heterogeneidades del medio, se producen múltiples reflexiones y la energía se redistribuye causando atenuación. Por otro lado, por diferentes factores se produce atenuación intrínseca. Para el caso de las rocas, este tipo de atenuación tiene origen principalmente en la fricción de los granos de la roca, junto al movimiento de fluidos que se encuentran al interior de los poros, al paso de la onda. La atenuación intrínseca en este contexto depende altamente del tipo de fluido saturante de los poros (Cabrera-Zambrano et al., 2022).
Un ejemplo de este efecto se reportó en los campos Valhall y Sleipner (campos de la petrolera Británica BP), donde se presenta un sistema petrolífero con acumulaciones de gas (Dvorkin y Mavko, 2006). La propagación de las ondas en medios con saturaciones de gas produce los efectos antes mencionados, causando que la onda no alcance las profundidades que son de interés en la exploración de yacimientos de hidrocarburos.
En este trabajo se estudió la propagación de ondas sísmicas para medios con atenuación, haciendo uso de una ecuación diferencial fraccionaria: la ecuación de difusión-propagación, la cual pondera el fenómeno difusivo y el fenómeno ondulatorio. En la primera parte, se describe la ecuación de difusión-propagación, la cual puede deducirse a partir de las relaciones constitutivas de la viscoelasticidad, tomando como función de relajación la utilizada por Kjartansson en su trabajo de 1979 (Kjartansson, 1979). Posteriormente, se muestra una ecuación similar, en una versión más general (Carcione et al., 2002); para estas ecuaciones, se establecen las características de la onda difusiva para diferentes valores del factor de calidad Q, es decir, para diferentes valores del orden de la derivada temporal, donde se determina que la velocidad de fase y la atenuación es función de la frecuencia (Zhu y Harris, 2014).
Para la simulación numérica del fenómeno, representado por la ecuación diferencial fraccionaria difusión-onda, se utilizó un esquema de diferencias finitas de cuarto orden para las derivadas espaciales; para la derivada temporal se estableció una fórmula de recursividad, es decir, para calcular un nuevo valor en el tiempo, se utilizaron algunos de los valores anteriores. Se deduce además un nuevo criterio de estabilidad numérica, criterio que dependerá del orden de la derivada temporal.
Teniendo en cuenta la solución numérica, se ilustra la propagación de la onda, cuando se varía el factor de calidad Q. Posteriormente, se muestra la propagación en dos modelos que ilustran los sitios de acumulación de hidrocarburos, y en particular de acumulación de gas.
Marco teórico
Existen diferentes enfoques para llegar a la ecuación diferencial fraccionaria onda-difusión, para la cual el orden de la derivada temporal está entre 1 y 2, es decir, una ecuación intermedia entre la ecuación de difusión y la ecuación de onda. El punto de partida son las llamadas relaciones constitutivas para materiales viscoelásticos (Carcione et al., 2002):
donde t es el tensor de esfuerzo; ε, el tensor de deformación; j es la función de fluencia lenta, y * hace referencia a la operación de convolución. En el caso particular de que la función de fluencia lenta responda a una ley de potencia respecto al tiempo, esta será de la forma:
Donde M0 es el módulo volumétrico, r es la función Gamma, t0 es el tiempo de referencia, v es un parámetro adimensional y H(t) es la función Heaviside. Si v=0, la respuesta J(t) es instantánea, es decir, corresponde a un material elástico.
Tomando las ecuaciones de movimiento de los medios continuos y de la definición del tensor de deformación:
donde el subíndice indica derivación. Si reemplazamos (4) en (1), se obtiene:
Derivando la ecuación (5) respecto a x, y utilizando la ecuación de movimiento (3), se obtiene:
Aplicando la transformada de Laplace a la expresión (6), en el dominio (x,s) esta expresión se convierte en:
Tomando la expresión de fluencia lenta propuesta por Kjartansson (1979), dada por la ecuación (2), para la cual
, donde
. Reemplazando la expresión de fluencia lenta en la ecuación (7), se obtiene:
Tomando la transformada de Laplace inversa se obtiene la ecuación diferencial de orden fraccional en el tiempo:
Esta es la ecuación diferencial de difusión onda 1D. Si se extrapola este resultado a dimensiones superiores (2D, 3D), asumiendo una ecuación diferencial parcial (2D) fraccionaria en el tiempo, se obtiene:
Donde β=2-2v y D, una constante positiva (Carcione et al., 2002). Si se toma una solución de onda plana:
reemplazando en la ecuación (10), se obtiene la siguiente relación de dispersión:
definiendo la velocidad compleja
, donde m es la frecuencia angular y k es la magnitud del vector de onda k2 = k2
x + k2
z de la ecuación (11), se puede obtener una expresión para V:
Si β=2, entonces
, que es el caso de la relación de dispersión para el caso elástico.
Para identificar completamente la ecuación diferencial (10) y la expresión de la velocidad de fase dada por (12), falta determinar D y β. Se debe recordar que para el modelo de Kjartansson la función de relajación viene dada por:
dado que la relación constitutiva (1) puede ser escrita en forma equivalente como:
tomando la transformada de Fourier de la expresión (14):
La transformada de Fourier de la función ˙Ψ(t) es ℑ{Ψ(t)} = Ψ(ω) = M(ω), donde:
Ψ(ω) se llama modulo complejo (Carcione, 2007); este módulo, el cual es en general una función de variable compleja, permite definir la velocidad compleja V (similar a la ecuación 12):
donde se ha llamado Ψ(ω) como M(ω). Igualando las expresiones de la velocidad compleja (12) y (17), por un lado, igualando las respectivas potencias de m, se obtiene que β=2-2v, por otra parte, se obtiene también que
.
Sustituyendo las expresiones de D y β en la ecuación (10) se obtiene la ecuación diferencial fraccionaria:
Esta ecuación (en la versión 2D) es la ecuación fundamental para simular la propagación-difusión de onda en medios con atenuación; dichos medios están caracterizados por su factor de calidad Q. La expresión para Q en términos de la velocidad compleja V viene dada por Carcione (2007):
utilizando la ecuación (16) y (17) en (19) se obtiene:
Esta ecuación establece la relación entre el factor de calidad Q y el exponente de la ley de potencia para la función de relajación o de la función de fluencia en el modelo de Kjartansson. Si v = 0 (β=2), entonces Q → ∞, esto quiere decir que es un material elástico. Dado que el orden de la derivada es β = 2-2v , de la ecuación (20) se puede establecer la relación entre el tipo de material por donde se propaga-difunde una onda y el orden de la derivada fraccional. Ya no se toma un orden único (dos para el caso de la ecuación de onda elástica), sino que el orden de la derivada temporal dependerá del tipo de material, es decir, β = f(Q). A continuación, se muestra en la Figura 1 dicha relación funcional.
De acuerdo con la Figura 1, para valores del factor de calidad entre 1 y 10, el orden de la derivada crece rápidamente. Se puede afirmar que para valores del factor de calidad mayores que 20, la ecuación diferencial fraccionaria se aproxima más a la ecuación de onda que a la ecuación de difusión; el orden de la derivada crece lentamente, tendiendo asintóticamente a 2, el orden de la derivada para la ecuación de onda normal.
De las ecuaciones (16) y (17) puede deducirse la velocidad de fase y el factor de atenuación. La velocidad de fase c viene dada por la expresión (Carcione et al., 2002):
y la atenuación α como:
Puede deducirse que la velocidad de fase puede expresarse en términos del exponente de la ley de potencia v:
con
. Similarmente, el factor de atenuación es:
Donde α es la atenuación y v está relacionado con β = 2-2v, que es el orden de la derivada fraccionaria. Utilizando la ecuación (20) puede expresarse a la velocidad de referencia c0 en términos del factor de calidad Q, como se muestra en la Figura 2.
Cuando el factor Q aumenta, el valor de c0 tiende asintóticamente (por encima) al valor
. En este caso, se tomó como valor de referencia 1500, es decir, para cada material se toma un valor de referencia c0 tal como se muestra en la Tabla 1.
Tabla 1 Velocidad de referencia y factor de calidad para diferentes materiales.
| Material | Velocidad de referencia c 0 (m/s) | Factor de calidad |
|---|---|---|
| Capa meteorizada | 450 | 10 |
| Arcillas | 1500 | 20 |
| Arenas consolidadas | 3500 | 30 |
| Calizas | 5000 | 40 |
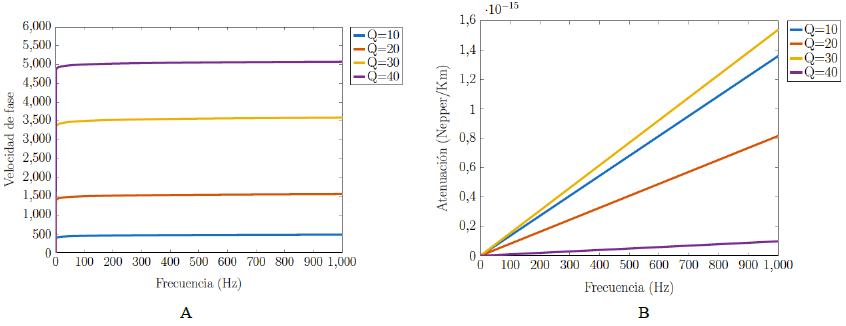
De otra parte, a partir de las expresiones (23) y (24) se puede estudiar el comportamiento de la velocidad de fase (c) y la atenuación (a) en función de la frecuencia para diferentes valores del factor de calidad Q. En el siguiente experimento se tomaron valores de c 0 , así como también diferentes valores de Q, desde un material no consolidado como las capas meteorizadas, hasta las rocas duras tipo calizas (Wang y Cai, 2017). Como era de esperarse, los materiales menos consolidados serán los de mayor atenuación (Figura 3B) y de menor velocidad, es decir, los materiales de menor factor de calidad Q (Tabla 1); por el contrario, para los materiales rígidos como las calizas o las arenas consolidadas, las ondas acústicas tendrán una mayor velocidad de propagación y su atenuación será mucho menor, es decir, valores del factor de calidad Q más altos.
Solución numérica de la ecuación de difusión-propagación
En la expresión Pn m,j = P (tn, xm, zj), el índice n indica paso temporal, y los índices m y j se refieren a los pasos de malla espaciales x, z, respectivamente. Teniendo en cuenta esta notación, para resolver la ecuación (18) se usa un esquema de diferencias finitas de cuarto orden para hacer la aproximación del Laplaciano:
donde Δs son coeficientes determinados del esquema de diferencias finitas de cuarto orden, donde
(Liu y Sen, 2009) y Δh es el paso en la dirección x y z, y la expresión para la derivada temporal es:
La derivada fraccionaria de P en un tiempo t depende de los valores previos de P; esta es la característica fundamental donde L es un entero positivo para el cual el coeficiente binomial
, para k ≥ l. Donde
y L es la longitud de memoria efectiva, es decir, es el número de términos anteriores (en el tiempo) de P que se guardan para el próximo cálculo. Los coeficientes c
k
para valores diferentes de y definen el fenómeno, es decir, y = 0,5 obtiene los coeficientes para la aproximación de la ecuación de calor, análogamente si y = 0 son los mismos coeficientes determinados por la serie de Taylor para la aproximación de la ecuación de onda en diferencias. Por último, y = 0,25, que es un valor intermedio entre la ecuación de calor y la ecuación de onda, es decir, se tendrá un fenómeno propagatorio con pérdidas; para valores grandes de k, los coeficientes c
k
tienden asíntoticamente a cero.
Reemplazando las expresiones (25) y (26) en la ecuación (18) y despejando el término del tiempo n + 1 se obtiene finalmente la expresión discretizada de la ecuación:
donde Δh = Δx = Δz es el paso de la malla, Δt es el paso en el tiempo.
La ecuación (27) se reescribe usando la operación de convolución
donde
,
y el último término
.
Estabilidad numérica
La estabilidad numérica del esquema de diferencias finitas es usado para resolver la ecuación de difusión-propagación. La estabilidad se usa para garantizar que un algoritmo restrinja el tamaño del paso en el tiempo (Δt) para evitar la propagación de errores en la solución numérica. Para analizar la estabilidad numérica del esquema propuesto en la sección anterior se define el error
, considerando estos errores en la forma de solución de onda plana y monofrecuencial:
donde k x , k z son los componentes del vector de onda.
Sustituyendo la expresión (29) en el esquema de diferencias finitas descrito por la expresión (27) se tiene
Asumiendo que:
.
Donde
.
Así 2β < Sn, para n suficientemente grande, se estima S por S, donde S = 4 y se obtiene:
Luego la condición de estabilidad para el esquema numérico descrito por la ecuación (27) es:
Si y = 0 entonces la ecuación (33) representa la condición de Courant (Carcione et al., 2002) para un esquema en diferencias finitas de segundo orden en tiempo y en espacio de la ecuación de onda.
Metodología
Se desarrollaron 3 experimentos numéricos para modelar la propagación de las ondas usando la derivada fraccionaria. En el primero, se simula la propagación de un pulso en medios con diferentes valores de Q y un solo valor de velocidad; en el segundo caso se modela una trampa con valores de atenuación altos para simular una acumulación de gas, y en el tercer experimento se compara un sismograma real de un perfil sísmico vertical (VSP) con el sismograma obtenido mediante la propagación de las ondas, usando la litología de la trampa con valores de la velocidad y Q de un yacimiento, cuyos datos han sido interpretados previamente.
Ejemplo 1: se aplicó el modelamiento viscoelástico en la propagación de ondas a un medio homogéneo de 12000 m x 12000 m con cuatro valores de Q, como se muestra en la Figura 4. La velocidad de propagación es de 2,5 km/s en todo el modelo, y los valores de Q son 5, 10, 20 y 100. La fuente es una Wavelet Ricker de fase cero con una frecuencia de 20 Hz. La instantánea corresponde al tiempo 218,8 ms, y se observa el frente de onda para los 4 valores de Q. Las formas de onda se muestran en la Figura 5, que corresponden a la llegada de la onda en un punto ubicado en (4000 m, 4000 m). Un menor valor de Q produce un mayor retraso en la llegada de la ondícula, una mayor pérdida de energía y además las fases son diferentes para cada valor de Q. Nótese que cuando Q tiene un valor muy pequeño, el fenómeno propagatorio tiende a desaparecer, convirtiéndose en un fenómeno difusivo; al tener menor orden la derivada fraccionaria (Figura 1), el paso en x y z es de 25 m y el paso del tiempo calculado usando el criterio de estabilidad es de 0,5 ms.
Figura 4 Instantánea de las ondículas en un medio homogéneo de velocidad con diferentes valores de Q.
Figura 5 Formas de las ondículas a una distancia de (4000 m, 4000 m) de la fuente, para los medios con diferentes valores de Q.
Evaluando la solución analítica tomada de Carcione (2007) para un medio homogéneo con velocidad 2500 m/s y un Q de 20, se toma la convolución de la fuente con la función de Green; en la Figura 6 se muestra la comparación entre la solución analítica y la solución numérica.
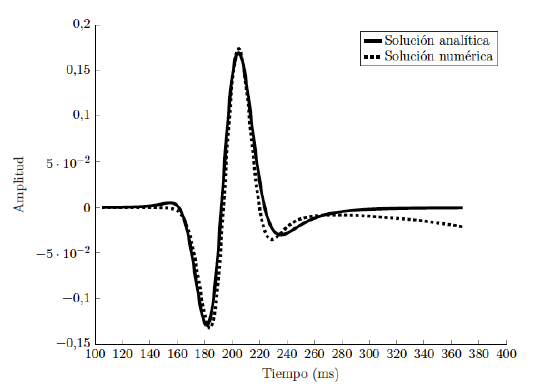
Figura 6 Comparación entre la solución analítica (línea continua) y la solución numérica (línea punteada), el receptor está a 350 m de la fuente.
Ejemplo 2: VSP sintético en un modelo de trampa con acumulación de gas. En este experimento se coloca en el modelo de una trampa petrolífera tipo anticlinal una zona de acumulación de gas (gap gas), caracterizado por un valor del factor de calidad Q=10; este valor significa que en dicha región la onda que se propaga sufrirá una alta atenuación.
En la Figura 7 se muestra el modelo geológico con los valores de Q para cada zona. Los valores de la velocidad y del factor de calidad Q están dados en la Tabla 2. El modelo tiene unas dimensiones de 4300 m x 4300 m. También se muestra el modelo de velocidad y las posiciones de los receptores, los cuales están espaciados desde los 1000 m hasta los 4300 m cada 300 m para una configuración de un registro VSP; el paso en x y z es de 10 m y el paso del tiempo calculado usando el criterio de estabilidad es de 0,1407 ms.
La zona de acumulación de gas genera mayor atenuación en la propagación de la onda, como se muestra en los sismogramas de la Figura 8. En las trazas grabadas en los receptores debajo de la zona de acumulación de gas se muestra mayor atenuación. En la Figura 9A se muestra la traza 6 en tiempo, y en la Figura 9B, en el dominio de las frecuencias. Para el caso de acumulación de gas, la traza en el tiempo muestra una mayor atenuación y una mayor dispersión en la fase. En el espectro de frecuencias se visualiza más pérdida de altas frecuencias y mayor corrimiento del pico de la frecuencia hacia las bajas frecuencias.
Tabla 2 Modelo de velocidades y valores de Q para simular con y sin acumulación de gas, donde cambia el valor de Q en el estrato 3.
| Estrato | Velocidad | Modelo Q con gas | Modelo Q sin gas |
|---|---|---|---|
| I | 2,8 | 20 (sin gas) | 20 |
| II | 3,0 | 30 (sin gas) | 30 |
| III | 3,4 | 10 | 40 |
| IV | 3,4 | 50 (sin gas) | 50 |
| V | 3,6 | 60 (sin gas) | 60 |
Ejemplo 3: comparación de los sismogramas sintéticos de un dato VSP original con el dato viscoacústico generado usando la derivada fraccionaria. Tomando la interpretación de los datos sísmicos de una adquisición en VSP, se construye el modelo de velocidad y se determinan los estratos y la ubicación de un sistema petrolífero o gas más aceite, como se muestra en la Figura 10. Para el cálculo del factor Q se usa el método de relaciones espectrales (Hauge, 1981) en el registro VSP. Dicho método consiste en establecer la relación (cociente) entre las diferentes trazas símicas en el dominio de la frecuencia para diferentes profundidades. Este cociente se puede aproximar linealmente; esta aproximación de la pendiente contiene la relación del factor Q. En la Figura 10 en la parte izquierda se muestra el dato sísmico procesado y migrado en profundidad; en la interpretación se puede determinar la trampa petrolífera, que corresponde a una trampa estructural delimitada por una falla. En la Figura 11A se muestra el modelo de velocidad, y en la Figura 11B, el modelo de Q; los valores de V, Q y los estratos se muestran en la Tabla 3.
Figura 10 A. Interpretación geológica de la zona donde están los pozos, B. ubicación de la fuente y receptores dentro del pozo (imágenes tomadas de Camacho, 2010).
Tabla 3 Modelo de velocidad y factor de calidad usados en el modelo.
| Estrato | Velocidad (km/s) | Q |
|---|---|---|
| I | 2,8 | 20 |
| II | 3,0 | 30 |
| III | 3,2 | 40 |
| IV | 3,4 | 50 |
| V | 3,6 | 60 |
| VI | 3,8 | 70 |
En la Figura 12 se muestra la propagación de la onda a través del subsuelo; se ilustran las reflexiones de la onda para diferentes tiempos: a 105 ms, 210 ms y 316 ms.
Para construir el dato VSP sintético se usó como fuente una Wavelet Ricker de fase cero con frecuencia dominante 34 Hz, con un muestreo de 2 ms. Se ubicó el inicio del pozo en la posición (0,0) y se utilizaron geófonos separados cada 20 m empezando en el punto (0,1370 m); el paso en x y z es de 10 m, y el paso del tiempo calculado usando el criterio de estabilidad es de 0,2634 ms. En la Figura 13A se muestra el sismograma real de la adquisición, y en la parte derecha, el sismograma modelado. Se puede apreciar una similitud entre el dato real y el sintético en la forma de las ondículas y la fase, sobre todo después de la traza 2; en la traza 1 el dato real contiene las ondículas ascendentes y descendentes, por lo que las trazas se superponen.
En la Figura 14A se aprecian la traza 4 real y la modelada, que corresponden al geófono colocado a 1025 m de profundidad. En la Figura 14B se muestran las dos trazas en el dominio de la frecuencia. El espectro muestra un corrimiento del pico de la frecuencia, de 34 Hz (frecuencia de la fuente) a 25 Hz(pico de frecuencia de la traza). En la Figura 14C y Figura 14D se muestra la traza 10 real y sintética a una profundidad de 1620 m, y el espectro de las frecuencias, respectivamente; el pico de las frecuencias está a 21 Hz.
Figura 14 A. Traza 4 en tiempo. B. Traza 10 en tiempo. C. Espectro de frecuencia de la traza 4. D. Espectro de frecuencia de la traza 10.
Análisis de resultados
En el experimento 1 se muestra la propagación de la onda en medios con diferentes valores de Q; se observa en el comportamiento de las ondículas que a mayor atenuación (inverso del factor de calidad), hay mayor pérdida de energía (Figuras 4 y 5). La pérdida de amplitud de la onda se relaciona con la atenuación, usando el modelamiento con la derivada fraccionaria, es decir, si el valor del factor Q es pequeño, el orden de la derivada temporal es cercano a 1 y se observa un proceso difusivo; y a mayor valor del factor Q, el orden de la derivada se aproxima a dos, que corresponde al fenómeno de propagación de ondas propiamente. Además, se observa un cambio en la fase en la forma de las ondículas debido al fenómeno de dispersión.
Para el experimento 2, donde se simuló la acumulación de gas en una trampa tipo estructural, los sismogramas muestran una mayor atenuación debajo de estas zonas; también se observa el fenómeno de dispersión en el cambio de fase en las ondículas y una pérdida de energía en las altas frecuencias, lo cual conlleva a un corrimiento en el pico de las frecuencias (Figura 8).
En el experimento 3, se comparó un dato real VSP con un sismograma modelado usando la derivada fraccionaria. El valor del factor de calidad del modelo es calculado por el método de relaciones espectrales usando el sismograma del VSP real. Se pudo determinar la similitud en los sismogramas real y modelado comparando las trazas en tiempo y en el dominio de la frecuencia (Figuras 13 y 14), lo cual nos permite inferir que la simulación de la propagación de ondas usando la derivada fraccionaria es útil porque incorpora el fenómeno de atenuación en el modelado, haciendo coincidir la pérdida de amplitud en el dato modelado con el dato real. En el dominio de la frecuencia también se determinó que los picos de las frecuencias son similares a los obtenidos en el dato real, lo cual confirma la pérdida de amplitud en las altas frecuencias y el corrimiento del pico de la frecuencia hacia las bajas frecuencias, que es lo usual en la propagación de ondas en medios anelásticos con atenuación intrínseca.
Conclusiones
El modelamiento con la derivada fraccionaria permite simular el fenómeno de atenuación en la propagación de ondas, ya que el orden de la derivada está íntimamente relacionado con el factor de calidad o la atenuación.
Para solucionar la ecuación difusiva-ondulatoria se utilizó el método de las diferencias finitas de cuarto orden para el Laplaciano, y en la derivada temporal se usaron los valores previamente calculados de la variable P, tomando un máximo de valores anteriores de L=30. Se halló, además, un criterio de estabilidad general del esquema de diferencias finitas para la ecuación diferencial con orden fraccionario de la derivada temporal.
De los tres experimentos se concluye que a medida que el factor de calidad es más pequeño, el orden de la derivada temporal se acerca a 1 y el fenómeno tiende a ser difusivo. Al incrementar el factor de calidad, aumenta el orden de la derivada temporal y el fenómeno tiende a ser ondulatorio.
El factor de calidad Q está relacionado con los materiales que componen los estratos, por consiguiente, el modelamiento usando la derivada fraccionaria refleja el comportamiento real de la propagación de la onda en estas estructuras, sobre todo cuando hay alta atenuación (Q bajo) de la onda debido, entre otros, a la acumulación de gas en la roca acumuladora que hace parte de cierto tipo de trampa de hidrocarburos.
