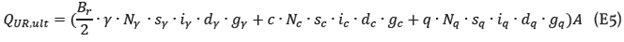INTRODUCCIÓN
En la proyección de edificios es usual que los ingenieros asuman que las estructuras tienen su base empotrada, por lo que se desprecia la interacción suelo-estructura (ISE), a pesar de que este criterio solo puede ser válido cuando estas descansan sobre estratos de suelos rocosos poco deformables. Cuando esto no sucede, las rotaciones y desplazamientos en la cimentación generadas por las deformaciones del suelo traen consigo un cambio en las condiciones de apoyo de la estructura, lo que genera una redistribución no prevista de las tensiones e incrementos en las deformaciones. Además, la deformabilidad del suelo cambia el comportamiento dinámico de las edificaciones, principalmente el periodo [1], lo que puede provocar errores en los diseños.
En la ISE es necesario identificar una serie de reacciones que, aplicadas simultáneamente a la masa de suelo y a la estructura de cimentación, den como resultado la misma configuración de desplazamientos diferenciales entre los dos componentes. Para lograrlo se deben crear simulaciones matemáticas que modelen el comportamiento del suelo con precisión; esto se hace a través de modelos constitutivos que emplean el método directo de ISE. Se requieren idealizaciones del material y de las condiciones de carga para simplificar la expresión matemática porque es imposible tener en cuenta todos los factores que afectan la respuesta mecánica del suelo bajo diferentes condiciones de carga. Estas idealizaciones incluyen las características primarias del material mientras omiten sus características menos significativas. Estos modelos tienen que estar basados en el tipo de análisis que se quiere adelantar (estático o dinámico) [2]; por un lado, están los modelos discretos, basados en la hipótesis de Winkler, en los que el suelo se reemplaza por resortes con una rigidez predeterminada, y los modelos continuos o directos, en los que el suelo se modela completamente junto con la estructura [3]. Estas han sido las dos direcciones principales en las que se ha desarrollado la búsqueda de modelos de comportamiento para describir el ISE. La idealización más precisa es la directa porque hace uso de métodos numéricos.
Diferentes tipos de estructuras han sido objeto de estudio al considerar la ISE, incluidas las edificaciones de gran altura, torres para aerogeneradores, telecomunicaciones o de transmisión eléctrica [4]. Los parámetros que influyen en el comportamiento de la ISE son: la rigidez del suelo, que puede ser cuantificada a través de la velocidad de la onda cortante; el módulo de elasticidad del hormigón utilizado en la cimentación [5]; además del tipo y forma de aplicación de las cargas [6]. Se ha comprobado que la ISE modifica la respuesta estructural de las edificaciones, lo que origina cambios en los periodos de oscilación [7], [8] el amortiguamiento de las cimentaciones[9] y los desplazamientos [10]; además, provoca que las fuerzas interiores se redistribuyan de los elementos estructurales [6], [7] y la cimentación. En relación con la influencia que tiene el viento en la ISE, Zhou, et al. [10] demostraron cómo la interacción in crementa el desplazamiento horizontal de una edificación cuando actúa la carga de viento. Esto se debe a que el periodo de la estructura aumentó después de considerar la ISE y el viento es una carga dominante para largos periodos, lo que hace que el sistema se vuelva menos rígido y permita mayores desplazamientos.
La interacción estática suelo-estructura está dada por las condiciones estáticas de carga -también puede ser en condiciones dinámicas-, lo que deriva en la interacción suelo-estructura dinámica. En la interfase de la estructura de cimentación y el suelo se originan desplazamientos debido a las cargas que transmite la cimentación, lo que lleva a la generación de desplazamientos totales y diferenciales.
En este trabajo se evalúa la interacción suelo-estructura en condiciones estáticas en las fuerzas interiores, los desplazamientos horizontales y modos de oscilación de un edificio cuando actúa la carga de viento. Con este objetivo, se modelará numéricamente una edificación y se le asignarán cargas gravitatorias y de viento con enfoque estático equivalente, a través del método factor efecto de ráfaga. Asimismo, se analizará la edificación con apoyos empotrados (sin interacción), cuyo modelo con ISE será continuo o directo, donde la masa de suelos y el edificio se modelarán de forma íntegra.
MATERIALES Y MÉTODOS
La edificación objeto de estudio tiene 100 metros de altura, consta de 27 niveles y ocupa un área en planta de 870 m2, aproximadamente, con sistema constructivo compuesto por losas apoyadas sobre columnas directamente y tímpanos. El tímpano se ubica en la zona central de la edificación y tiene 35 cm de espesor, las columnas disminuyen sus secciones con el aumento de los niveles y las losas de entrepiso son de 30 cm de espesor. En todos los elementos el material empleado es hormigón armado con 35 MPa de resistencia a compresión. Para la modelación del edificio se empleó el software con base en el método de los elementos finitos Midas GTS NX. Las columnas fueron modeladas como elementos beam y las losas y tímpanos como elementos plate discretizados con mallas del tipo híbrida con un espesor máximo de elementos de 80 cm. Las uniones entre los distintos elementos estructurales son continuas; en la Figura 1 se muestra el modelo geométrico de la edificación. Así mismo, se analizó la no linealidad geométrica para determinar si tiene influencia en la respuesta de la edificación, para lo cual se utilizaron como variable de control los desplazamientos verticales en una de las losas, cuyos valores se compararon en un modelo con comportamiento lineal y otro no lineal. El método iterativo empleado en el análisis no lineal fue Newton-Ramphson con un criterio de convergencia de desplazamientos del 0,1 %. Los resultados mostraron que los desplazamientos no cambian para un caso u otro, por tanto, se puede asumir el modelo con comportamiento lineal geométrico.
Se consideraron cargas de uso con un valor de 1,5 kN/m2 para los entrepisos y 1 kN/ m2 para la cubierta [11]; la carga permanente en los entrepisos tiene un valor de 2 kN/ m2. La carga de viento fue distribuida linealmente en dirección horizontal sobre los entrepisos.
Carga de viento
La carga de viento fue analizada en la dirección que genera mayores fuerzas, dado que se encuentra en una zona expuesta al mar abierto en la región occidental de Cuba. Para el alcance de este trabajo, solo se tuvo en cuenta la componente longitudinal del viento. La ecuación 1 se utiliza para determinar la fuerza del viento que se debe aplicar a un edificio de acuerdo con el método del Factor de efecto de ráfagas [12]:
Donde q 10 es la componente media presión básica del viento con un valor de 0,66kN/ m2, c h es el coeficiente de altura, ct es el coeficiente de recurrencia que es 1 para un periodo de retorno de 50 años, c r el coeficiente de ráfaga y el cf coeficiente de forma
(0,8 a barlovento, -0,5 a sotavento, -0,6 en los laterales y -0,8 en la cubierta) y A ref área de referencia o área tributaria. C D es la componente dinámica que puede ser longitudinal, transversal o torsional. Se tiene en cuenta si la frecuencia de oscilación del modo principal de la edificación es mayor a 1 Hz. Para el alcance de este trabajo solo se considera la componente longitudinal que está definida por la ecuación 2:
En la ecuación 2, G L es el factor efecto de ráfaga longitudinal, I (ze) intensidad de turbulencia para la altura de referencia (60 % de la altura de la edificación). La frecuencia de oscilación empleada para calcular la carga de viento fue la obtenida en el modelo empotrado con un valor de 0,38 Hz.
Suelo
La definición del suelo en el modelo con ISE fue evaluada a través de la incorporación de un suelo heterogéneo con tres estratos de suelos, uno con consistencia blanda, otro con consistencia media y un estrato rocoso a partir de los 40 m de profundidad. La selección de las propiedades del suelo se hizo a través de los datos brindados por Das et al. [13], que correlacionan la rigidez de los suelos con otras propiedades. En las Tablas 1 y 2 se muestran los parámetros y propiedades de los suelos deformables seleccionados para soportar al edificio y representar la ISE:
La cohesión no drenada (Cu) es necesaria para la determinación de la capacidad de carga de los pilotes, porque es el caso más crítico de diseño; esta puede ser correlacionada con los valores de índice líquido de los suelos a través de la ecuación 3, expresión empírica propuesta por Shimobe, et al. [14]:
Donde
 es el coeficiente de sensibilidad, cuyo valor está en función del tipo de suelo [13]. Los resultados obtenidos se resumen en la tabla 3:
es el coeficiente de sensibilidad, cuyo valor está en función del tipo de suelo [13]. Los resultados obtenidos se resumen en la tabla 3:
El suelo se modeló empleando el método de los elementos finitos. Es necesario proveer al modelo de características tensodeformacionales representadas a través de los modelos constitutivos que tengan en cuenta el comportamiento elastoplástico del suelo. Estos modelos deben basarse en el tipo de análisis (estático o dinámico) que pretenden realizar [2]. El modelo de Mohr-Coulomb, por su relativa simplicidad y su carácter general, es uno de los más empleados en los problemas de ISE, en general [15], [16], y es el seleccionado para describir el comportamiento de los estratos de suelos deformables en este trabajo.
A partir de los 40 m de profundidad, se encuentra un estrato rocoso. Los parámetros que se analizan en las rocas son diferentes a los de los suelos, de manera general; en este caso, se tiene una roca sedimentaria clástica conglomerada. Para la modelación de la roca se debe emplear el modelo de Hoek, et al. [17], que depende del índice de resistencia geológica (GSI, por sus siglas en inglés) y de los parámetros adimensionales m y s.
En la Tabla 4 se muestra el tipo de roca y los parámetros del modelo de Hoek, et al. [17] que la definen:
En la Tabla 5 se resumen los parámetros necesarios para poder implementar el modelo de comportamiento de Hoek, et al. [17].
Para garantizar que en los límites del modelo las tensiones sean cero, se comprobó que, para un valor de 70m de profundidad y 225m para los lados de la masa de suelos, se alcanza esta condición. En la Figura 2 se muestra la configuración final del modelo directo utilizado para analizar la ISE:
CONDICIONES DE APOYO
En este estudio se evalúa la implicación que tiene la interacción suelo-estructura en las fuerzas interiores de la edificación, para lo cual se modelará una variante en la que el edificio se considera empotrado en su base, y otra en la que el efecto de la interacción sea tenido en cuenta a través de un modelo directo.
La cimentación empleada fue de losas combinadas con pilotes con criterios de diseño en los que se estima la capacidad de carga de la losa en conjunto con los pilotes [18], [19], [20], [21].
Una cimentación de losas combinadas con pilotes (PR) consiste en tres elementos: el suelo, la losa y los pilotes. Una carga externa aplicada (Q) es equilibrada en una parte con la presión de contacto que se genera entre la losa y el suelo (Q ur ), y en otra parte, con aquella generada entre el grupo de pilotes y el suelo (QG). Para conocer la proporción de carga que soportan los pilotes, de Sanctis et al. [20] proponen emplear el siguiente coeficiente definido por la ecuación 4:
Las cimentaciones de losas combinadas con pilotes (PR) cubren el rango de 0 < αPR < 1 . La capacidad de carga de una losa de cimentación (α PR = 0) es evaluada a través de la ecuación 5, que es la empleada para determinar la capacidad de carga en cimientos superficiales en general:
Donde B r es el ancho de la losa, A es el área de losa, los coeficientes N son los de capacidad de carga 5, los de forma, i de inclinación de la carga, # inclinación el terreno, d el de profundidad, c la cohesión del suelo, q la presión efectiva en el fondo de la losa y γ el peso específico del suelo.
La losa de cimentación tiene unas dimensiones en planta de 32x32 m y un espesor de 1,5 m. Fue diseñada geotécnicamente empleando el método de estados límites para ambos modelos. En el caso del modelo de suelo con consistencia blanda, no se cumplió la capacidad de carga y fue necesaria la introducción de 324 pilotes para incrementar la capacidad de carga de la cimentación. En la Figura 3 se muestra el diseño final de la cimentación en el modelo con ISE:
En el contacto de la losa con el suelo se crean elementos de interfaz. La modelación se hizo por etapas constructivas. Para la primera, en la que no hay interacción aún y la interfase no es necesaria, se deben asignar vínculos rígidos a los nodos que quedan separados por la interfase para evitar errores en el análisis. Ya en la etapa de interacción este vínculo debe ser removido. El material de la interfaz está en función de la rigidez de los elementos adyacentes, a través de los módulos de rigidez normal, definido por la ecuación 6, y el tangencial, definido por la ecuación 7:
C i , G i y E oed,i cohesión, módulo cortante y módulo edométrico reducidos (ecuaciones 8-10).
t v : Espesor virtual de la interfase, varía entre 0,01 y 0,1, cuanto menor sea el valor, mayor será la diferencia de rigidez entre el suelo y la estructura. En este caso, la diferencia de rigidez entre el suelo y el concreto es significativa, por lo que se elige el valor de 0,01.
Donde
v i : Coeficiente de Poisson de la interfase, vale 0,45 para la interfase. Se emplea este valor para simular el comportamiento friccional no compresible y evitar errores numéricos.
R: Es el coeficiente de reducción de la rigidez (de 0,7 a 1 para el contacto arcilla-hormigón). Se considera con un valor de 0,8.
RESULTADOS Y DISCUSIÓN
La influencia de la ISE en los desplazamientos horizontales máximos de la edificación, que ocurren en el último nivel producto de la carga de viento, se muestra en la Figura 4 para modelos con y sin ISE:
En el análisis de ISE el suelo y la superestructura funcionan como una estructura única, por lo que una disminución en la rigidez de uno de los dos influye en el otro. Es por esto que, cuando se considera la ISE, los desplazamientos horizontales en el último nivel del edificio se incrementan en un 166 % como se evidencia en la Figura 4, lo que tiene una influencia significativa en las frecuencias de oscilación. Para determinar el impacto de la ISE en las frecuencias de oscilación, también se evaluó esta variable; en la Figura 5 se muestran los valores obtenidos en los seis primeros modos:
Los resultados muestran que la influencia de la ISE disminuye las frecuencias de oscilación de la edificación, con diferencias más significativas en los dos primeros modos, en los que la reducción fue de un 16 y un 26 %, respectivamente. El hecho de que los modelos con ISE tengan frecuencias menores a 1 Hz en más de un modo tiene como implicación que la determinación de la fuerza del viento no puede ser calculada por el método factor efecto de ráfaga, sino por otros métodos dinámicos.
El aumento de los desplazamientos horizontales y la disminución de las frecuencias de oscilación tienen un impacto directo en cómo se distribuyen las fuerzas internas dentro de la superestructura.
Las fuerzas interiores fueron evaluadas estableciendo elementos estructurales de referencia que tuvieran la misma ubicación en cada modelo. En la Figura 6 están los resultados de fuerza axial para columnas ubicadas en una de las esquinas del edificio, y en la Figura 7, para una de las columnas interiores. Este análisis se hizo para todos los niveles de la edificación con el objetivo de determinar si varía su comportamiento con el incremento de altura.
De los resultados mostrados en las Figuras 6 y 7, se aprecia que la interacción suelo-estructura no tiene una influencia significativa en la variación de la fuerza axial en las columnas de esquina e interiores. Lo anterior se debe a que los desplazamientos verticales no son considerables, ya que su mayor valor fue de 97mm, y la ocurrencia de asiento diferencial, que es la que provoca los cambios en la redistribución de esfuerzos verticales en las columnas, es despreciable.
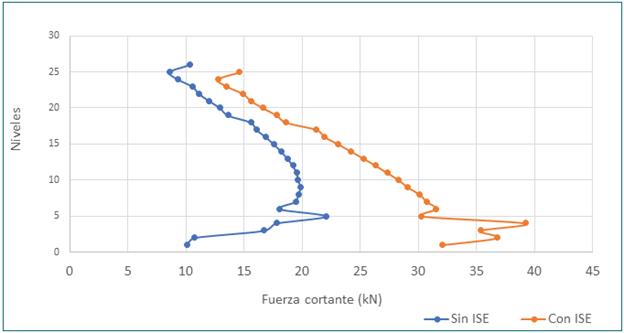
El efecto de la fuerza cortante también fue evaluado en las mismas columnas; los resultados obtenidos se muestran en las Figuras 8 y 9:
Los resultados de influencia de la ISE en la fuerza cortante de las columnas muestran que la consideración de ISE incrementa los valores de fuerzas interiores en todos los niveles, lo que resulta más evidente para las columnas interiores con valores mayores al doble del modelo sin ISE en la mayoría de los niveles. La diferencia entre la fuerza cortante del modelo con ISE y sin esta se debe al asentamiento vertical y la rotación que tiene lugar en la cimentación por la acción de las cargas horizontales extremas. La consideración de este efecto en el modelo continuo de ISE produce desplazamiento en los elementos de soporte vertical (columna), lo que incrementa el valor de la fuerza interior de cortante.
Las fuerzas interiores también fueron evaluadas en los tímpanos o muros cortantes. Las fuerzas membranales se seleccionaron para cuantificar la influencia de la ISE en estos elementos. En la Figura 10 se muestran los resultados obtenidos para todos los niveles del edificio:
El impacto de la ISE en las fuerzas membranales desarrolladas en el tímpano es significativa en los primeros 10 niveles, con diferencias entre un 10 y un 15 %; a partir de esta altura, la influencia de la ISE en esta variable deja de ser significativa. Al igual que en las columnas, esta baja diferencia se debe a que los desplazamientos verticales no son significativos y el tímpano es una estructura de gran rigidez.
Los resultados de fuerzas interiores muestran que la consideración de la ISE provoca redistribución de fuerzas en los elementos estructurales de la edificación, principalmente, la fuerza cortante en las columnas, donde hay elementos que pueden estar sometidos a mayores solicitaciones, y otros, a menores, según sea el caso.
CONCLUSIONES
Se estudió un edificio de 100 m de altura sometido a una carga de viento extrema, apoyado sobre una losa combinada con pilotes. El análisis de ISE en condiciones estáticas llevado a cabo en este estudio demuestra que esta no se debe despreciar en suelos deformables y cimientos flexibles. Para su consideración, se empleó el método directo, que representa con mayor rigor el fenómeno físico de interacción tridimensional que tiene lugar para esta tipología de cimentación, en la que se garantiza una correcta distribución de tensiones en el contacto del suelo con la cimentación. Así mismo, se estima la flexibilidad de la losa y su interacción con el suelo y los pilotes, lo que constituye una ventaja por encima de los métodos discretos o winklerianos.
Los resultados obtenidos muestran que la ISE afecta de manera significativa la respuesta estructural de la edificación de 100 m de altura. La disminución de rigidez del suelo hace que disminuyan los valores de frecuencia de oscilación, cuando es considerada la ISE, y que aumenten los desplazamientos horizontales. La redistribución de tensiones provocada por este efecto incrementa los valores de fuerza cortante en los elementos tipo barras, lo que no ocurre para la fuerza axial. En el caso de los tímpanos, la influencia de la ISE no es considerable.
Los resultados obtenidos motivan futuras investigaciones en las que se evalúen la influencia del tipo de suelo, la profundidad de cimentación de la losa, la altura de las edificaciones y la forma de aplicación de la carga de viento, con base en otros métodos para calcularla como el de dominio del tiempo. La interacción suelo-estructura debe considerarse siempre en el análisis de edificaciones sobre suelos deformables; despreciar esto y optar por los apoyos rígidos podría derivar en errores en el diseño de los elementos estructurales.