Introduction
Voice production involves the integration of three physiological processes: breathing, phonation, and resonance, allowing for the analysis of aerodynamic, mechanical, and acoustic phenomena within this framework [1,2]. In general terms, sound production is a complex nonlinear process involving air-structure-sound interaction: pulmonary pressure (subglottic pressure) generates airflow, which in turn interacts with the glottis, the region where the vocal folds converge to initiate vibration as a result of the interplay between air and the surrounding tissues and mucosa [3,4]. The quality of sound production is significantly influenced by the airflow [5]. Under optimal physiological and geometrical conditions, the interaction between the airflow and the vocal folds leads to a self-oscillation effect [6,7]. Consequently, the airflow affects glottal geometry, and the biomechanical properties of the vocal folds bring about alterations in the conversion of this airflow into sound, ultimately influencing the quality and acoustic attributes of the voice (i.e., the voice's characteristics depend on the interplay between flow and structure) [8]. Finally, the sound generated in the glottis is modified in the supraglottic cavities, so the concept of vocal tract inertance also contributes to this self-oscillation [2] (see Figure 1).
Given the complexity of this field, research has primarily focused on comprehending the various physical phenomena of vocal production through biomechanical modeling. In the literature, models of varying complexity have been developed to represent vocal fold tissues, incorporating lumped elements to depict acoustic wave signals and one-dimensional airflow [9,10]. Also, models of greater complexity, with a representation of computational fluid dynamics and high-fidelity, have been proposed [1].
Reduced-order models have proven effective in representing the self-oscillation and modal response of vocal folds, as demonstrated in recent works [11]. Other authors worked in models that include nonlinear flow-structure-acoustic coupling in voice production [12,13], and wave propagation within the vocal tract [2]. It is worth to mention the work of Espinoza et al. [14].
The ultimate objective of modeling vocal production has been to understand the vocal folds’ kinematic behavior; however, it is equally crucial to establish parameters for the clinical diagnosis of vocal pathologies. This purpose involves recognition of parameters related to vocal fold displacements and geometry concerning aerodynamic behavior. Some parameters that are currently challenging or even impossible to measure clinically can be estimated through numerical models, yielding a series of synchronized signals and data [15]. For instance, this encompasses the estimation of impact forces during the collision of vocal folds upon reaching the midline and calculation of intraglottic pressure [16,17]. Additionally, other lumped-element models presently aid in characterizing hyper-functional behaviors in voice use, allowing for their classification into phonotraumatic and non-phonotraumatic categories [18]. This process considers parameters derived from estimation methods utilizing signals acquired by accelerometers in conjunction with pressure transducers, airflow transducers, microphones, and/or neck surface electrodes [19].
The gap between vocal production modeling and clinical utility has been a challenging aspect addressed by various numerical models. However, achieving this integration remains complex, primarily attributed to the reliance on measurements derived from in vivo, ex vivo experiments [20], or numerical simulations [12,16,21] for characterizing the voice and the structural mechanical properties of the models. While these approaches provide an approximation, they lack precision in mirroring the clinical reality of a patient with a vocal alteration. Models focusing on spring masses and dampers, in particular, face difficulty in accurately determining damping coefficients, owing to potential variations in representing the viscosity-elasticity of the vocal fold. This paper describes a parametric optimization of the Hertz model originally introduced by Horacek [16].
Thus, this work aims to conduct a parametric refinement of a mass-spring-damper-based vocal production model incorporating subglottic pressure interaction, enabling the representation of collision forces between vocal folds during phonation [16]. Section 4 elucidates the features of the model. The parametric refinement is executed through a comprehensive application of metaheuristic methods, aiming to reconstruct the physical behavior of the vocal folds and estimate the impact stress during phonation.
The paper is structured as follows: Section 2 provides the background information essential for a thorough comprehension of the presented problem; Section 3 delineates the model used to representing the impact stress of vocal fold; Section 4 furnishes preliminary insights into the parametric synthesis framework; Section 5 addresses the demonstration of the proposed parametric synthesis method; finally, Section 6 offers a discussion and outlines potential future research avenues within this domain of knowledge.
Background: Metaheuristic Methods
The model serves as an abstraction of a real-world problem, upon which mathematical considerations are applied to yield results tailored to the desired outcomes. Within the realm of modeling, traditional methods for optimization are employed [22]. Among these methods are metaheuristic algorithms, which encompass approximate optimization and general-purpose search algorithms. These algorithms iteratively guide a subordinate heuristic by intelligently integrating various concepts to effectively explore and exploit the search space towards an appropriate solution [23].
Such methods have found application in diverse problem domains. For instance, they have been employed in assignment problems utilizing piecewise linearization techniques [24], in the design of embedded computer systems through deterministic iteration techniques [25], and in engineering structure design based on signomial discrete programming [26]. Additionally, they have been utilized in deterministic optimization methods within engineering and management [27], as well as in the field of molecular biology to optimize the localization of protein binding sites on DNA strands [28]. Likewise, this methodology has been used in medical contexts for optimizing fractionated protocols in cancer radiotherapy via nonlinear programming [29]. Other applications encompass model updating in the parameter optimization process [30-32].
Furthermore, metaheuristic methods have contributed to the development of novel optimization techniques [33]. These techniques find utility across various domains of knowledge [34]. For example, they have been applied to tackle complex nonlinear problems using music-based metaheuristic search methods, as documented by Altay and Alatas [35]. Heuristic and metaheuristic approaches have also been proposed for genetic algorithm, and memetic algorithm optimization [36]. Similarly, variations of methods for restricted optimization have been suggested. For instance, Gokalp and Ugur [37] employed a hybrid way, integrating three metaheuristic algorithms of different behavioral patterns.
Within the realm of research applied to vocal models, only a limited number of contributions have been identified. Existing literature provides evidence of parametric estimation work, such as that proposed by Yang et al. [38], wherein a mathematical optimization method is introduced to adjust the parameters of a three-dimensional vocal model for reproducing vocal fold dynamics through the evaluation of biomechanical parameters (pressure, tension, and masses). Additionally, Kurniasih et al. [39] present a computational estimation of vocal tract shape parameters employing synthesis analysis with acoustic data as input to iteratively optimize the shape parameters. Similarly, Dognin [40] proposes parametric optimization for vocal tract length normalization. This theme is further explored in Laprie and Mathieu´s work [41], which introduces a variational computational approach for estimating vocal tract shapes from speech signals using iterative processes. Another noteworthy study is presented by Ding et al. [42], where a swift and robust joint estimation of the tract and vocal source parameters from speech signals is proposed, based on an autoregressive model with exogenous input (ARX). It is noteworthy that, as of the date of this study, no applications aimed at understanding the aerodynamic processes involved in vocal production have been identified in the literature review. One approach to fine-tuning model outputs involves the development of algorithms that facilitate the convergence of values leading to model stability.
Combinatorial algorithms represent one of the most commonly employed algorithmic approaches for fine-tuning a model's response [43]. These algorithms form an integral part of metaheuristic algorithms [44,45]. They systematically enumerate all potential candidates for solving a given problem, assessing whether each candidate satisfies the solution criteria. This algorithm is often applied when the pool of candidate solutions is small or when it can be selectively reduced through preceding heuristic methods [46,47].
Model to Represent Impact Stress of Vocal Fold
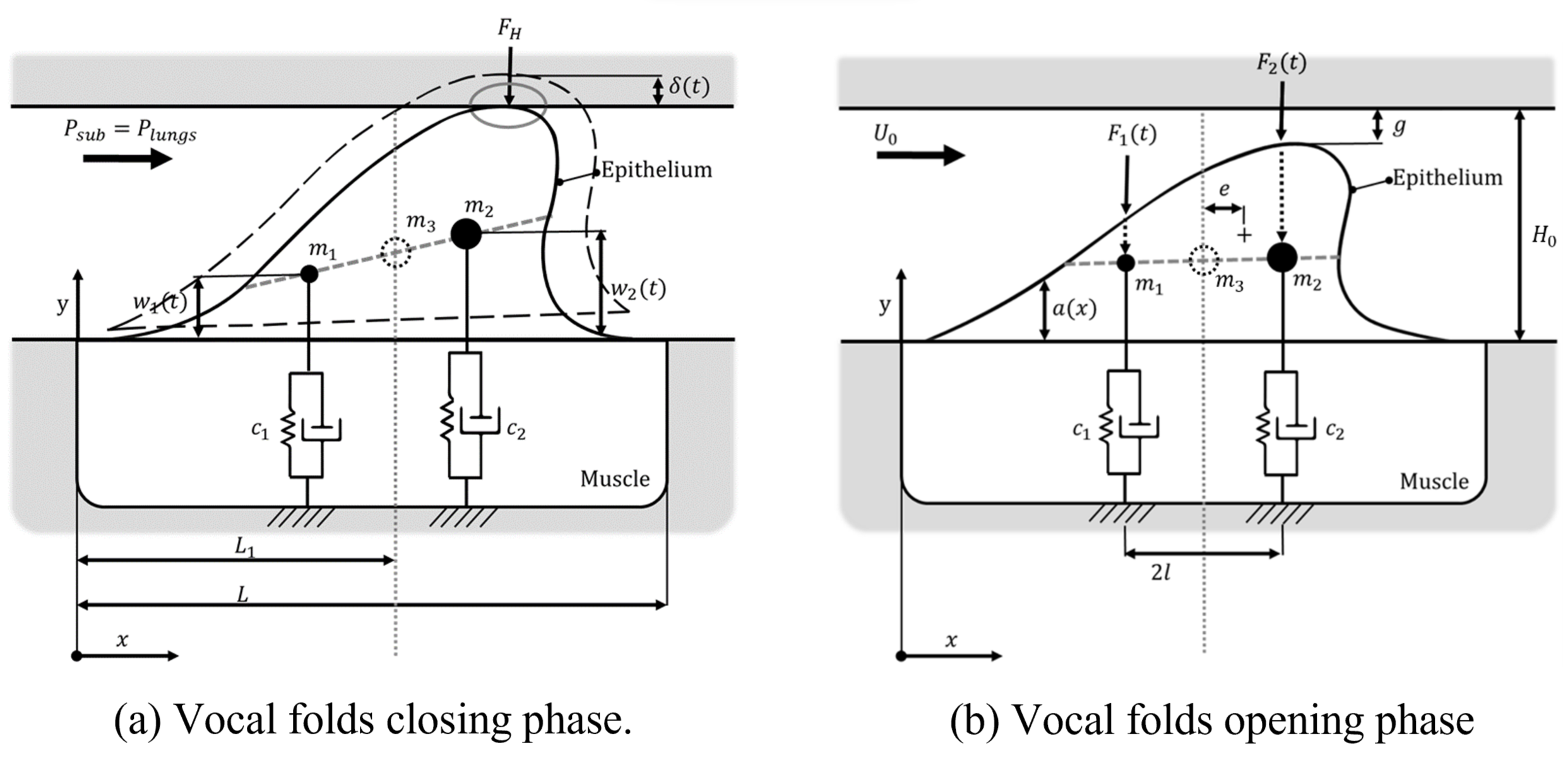
The model of vocal fold self-oscillation, as outlined by Horáček et al. [16,48] serves as the foundational framework. This is a two-dimensional aeroelastic computational model, which incorporates the Hertz model to account for impact forces governing vocal cord collisions [17]. The primary objective of this model is to investigate the maximum magnitudes of the impact stress (IS) throughout a complete cycle of vocal fold vibration. It is designed to simulate a single vocal fold, assuming glottal symmetry, and is tailored towards emulating the characteristics of a typical, healthy larynx.
Figure 2 illustrates a schematic representation of the model, conceptualized as a dynamic system characterized by two degrees of freedom. It comprises three equivalent masses oscillating on two springs, along with dampers regulating the opening and closing phases of the glottis. The motion is characterized by the rotation and translation of the components arranged in the configuration of a vocal fold. A succinct overview of the model is presented herein.
The interaction with the vocal tract is not taken into consideration by the model. Thus, only mechanical settings require adjustment. Self-oscillations arise from the presence of nonlinear aerodynamic forces and collision forces acting upon the static lung pressure load (Plung) when the glottis is closed. The geometry of the vocal cords is approximated by a parabolic shape function
The equation of motion for the two-degree-of-freedom vocal fold model can be written as,
where the following excitation and displacement force vectors were introduced:
and
Damping matrix
Incoming airflow velocity
The impact force in Hertz is expressed as
Where
where
Method
Parametric tuning procedure and algorithm configuration
The path-based search algorithm is commonly employed in theoretical and practical investigations of search metaheuristics [51]. It involves the utilization of environment structures, which encapsulate the notion of proximity or adjacency among alternative problem solutions. The entirety of solutions falls within the environment surrounding the present solution, demarcated by a solution generation operator. Path-based algorithms conduct a localized examination of the search space, scrutinizing the environment encompassing the current solution to determine the course of the search path [52]. Establishing the environment's structure suffices to formulate a generic search algorithm model [51]. To instantiate the algorithm, encoding for the solutions is specified, and a neighbor generation operator is defined, consequently establishing an environment structure for the solutions. Subsequently, a solution is selected from the environment of the current solution until the termination criterion is satisfied [53].
The parametric tuning of the biomechanical vocal fold model addressed in this study commenced with the initial parameters validated by Horacek [17], as previously reported. The configuration procedures of the tuning algorithm are meticulously outlined in Diagram 1, providing a precise delineation of the decision-making process within the algorithm.
The initial coefficients of the model were derived from the detailed biomechanical parameters described in the subsequent section, which comprehensively presents the model. These coefficients are directly linked to the matrices of the vocal fold mass-spring model, affording us the capability to modulate the composition of the folds to achieve the desired behavior.
The evaluation of the tuning process's performance was conducted by considering features of the target signal, including the period (T), positive maximum amplitude (Amax-p), negative maximum amplitude (A max-n ), positive section area (A r-p ), and negative section area (A r-n ). The appropriate moment to conclude the simulation is determined by the algorithm through an assessment of the discrepancies between the previously acquired characteristics and the desired ones. A margin of error of at least 10% was established, at which point the algorithm decides to conclude the metaheuristic search or update the data with new combinations, effectively restarting the simulation.
Figure 3 provides a visual representation of the employed methodology, illustrating the workflow during the parametric tuning of the biomechanical vocal fold model. This figure serves as an essential visual guide for comprehending the optimization process implemented in this scientifically significant study.
Results
Demonstration to parametric synthesis method
In this section, a summary of the results achieved following the successful implementation of the parametric synthesis method for the vocal model is presented. The fine-tuning adjustments made enabled the attainment of behaviors closer to the desired physiological parameters. This demonstrates the effectiveness of the approach applied in refining the biomechanical phonation model, thereby fulfilling the objective set forth in the title of the study.
The parametric synthesis method for the vocal model is implemented using a heuristic search algorithm. The parameters to which the fitting algorithm is applied are the elasticity coefficients
After approximately 360,000 iterations of possible combinations, the algorithm was halted to refine the coefficients of the model. The fine-tuning of the model is manifested in the vertical displacements of the masses represented by

Figure 4 Procedure for adjusting the vertical displacements of equivalent masses m1 and m2; comparing the obtained signals W1 and W2 Vs. the desired signals W1D and W2D.
The iterations of this algorithm were terminated upon reaching an error threshold of 10% or less for the evaluated features in the model signals. Table 1 presents the parametric modifications that the input variables underwent throughout the simulation. It is worth noting that the parameter ϵ 1 remained unchanged in its tuning, as dictated by the inherent nature of the mechanical model, wherein the dynamics primarily center around the forces generated by the viscous components rather than the mass of the fold.
Table 1 Tuning of parameters of the mechanical model of vocal folds.
| samples | c1 | c2 | ϵ1 | ϵ2 |
|---|---|---|---|---|
| 0 | 1,92E+13 | 4,50E+10 | 0,00 | 1,00E-04 |
| 100000 | 5,05E+12 | 1,18E+10 | 0,00 | 3,80E-04 |
| 200000 | 2,21E+12 | 5,18E+09 | 0,00 | 8,70E-04 |
| 300000 | 1,23E+12 | 2,89E+09 | 0,00 | 1,56E-03 |
| 310000 | 1,17E+12 | 2,75E+09 | 0,00 | 1,64E-03 |
| 320000 | 1,11E+12 | 2,62E+09 | 0,00 | 1,72E-03 |
| 330000 | 1,06E+12 | 2,49E+09 | 0,00 | 1,81E-03 |
| 340000 | 1,01E+12 | 2,38E+09 | 0,00 | 1,89E-03 |
| 350000 | 9,70E+11 | 2,27E+09 | 0,00 | 1,98E-03 |
| 360000 | 1,93E+12 | 4,54E+09 | 0,00 | 3,31E-04 |
Under similar conditions, it is important to observe that the simulation was concluded once errors had reached permissible thresholds (refer to Figure 5).

Figure 5 Error signals of the characteristics extracted from the desired signals WD Vs. signals obtained W.
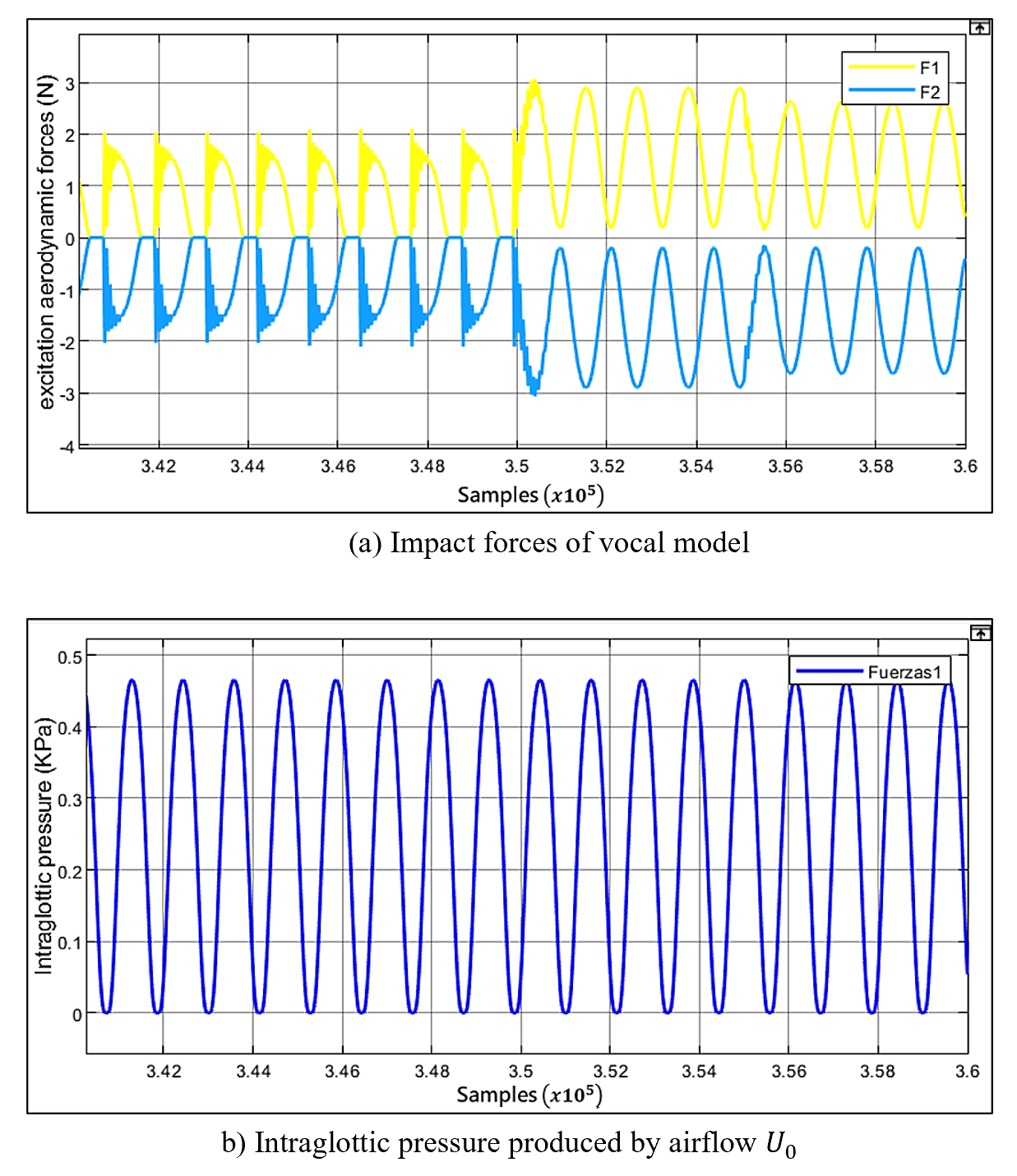
In the simulation processing time, fine-tuning took approximately 3.6 to 5 seconds on an Intel(R) Core (TM) i5-10210U CPU @ 2.11 GHz machine. A fixed simulation step factor of 0.00001 was employed, considering that oscillations typically range between 100 and 200 Hz. The parametric adjustment facilitated the acquisition of interaction forces exciting the vocal model. Figure 6a illustrates the excitation force curves of the mechanical vocal model in the final moments of the simulation, wherein the parameters approach their minimum error. It is noteworthy that starting from sample 350000, the forces exhibit sinusoidal coupling and adapt in accordance with the naturally obtained parameter conditions at this iteration instant.
In Figure 6b, aerodynamic forces (including impact forces and pressure variations between vocal folds) are presented, simulated using coefficient values derived from parametric tuning. The simulation employs a flow velocity of 1.6, yielding intraglottic pressures reaching as high as 0.46 [17]. This behavior exhibits fluctuations contingent on the opening or closing of the vocal folds.
Finally, Figure 7 displays the impact force curves computed using equations 3 and 4, incorporating the fine-tuned coefficients. We also present the curves for delta(t) (vocal fold penetration factor when applying equation 7). Note that, ymax)(t)>H0, which indicates the impact forces between the two vocal folds. Through parametric tuning of the model, we were able to attain impact forces of up to 2.5 and displacements of up to 1.
Discussion
I n this study, a parametric tuning approach using comprehensive metaheuristic methods was implemented to refine a vocal production model. This method allowed for the reconstruction of an approximate physical behavior of the vocal folds, enabling the estimation of impact stress resulting from the interaction forces between them. The tuning parameters, namely damping and spring coefficients, were systematically adjusted. Additionally, performance stopping criteria were established, comparing error characteristics between the desired and obtained signals, with an error margin of at least 10%.
As indicated by previous research [40], the effectiveness of tuning methodologies is intricately linked to the complexity of the model. Furthermore, achieving an optimal tuning hinges on the distinct vocal characteristics exhibited by male and female speakers, warranting tailored parameter variations [40]. While our results were validated with input parameters derived from a male speaker, it is crucial to acknowledge that gender-based differences in vocal frequencies may necessitate distinct tuning approaches.
The technique employed in this study addresses the estimation of impact forces through a parametric adjustment of the vocal characteristics within the Herz model, as examined by previous works [16]. This approach stands out for its organized exploration and exploitation of parametric targets, providing a unique opportunity to objectively quantify the biomechanical attributes of vocal folds [39], with a specific focus on acquiring data pertaining to impact forces. This aligns with the methodologies of global and local optimization algorithms, similar to those adapted in comparable studies, demonstrating their efficacy in yielding suitable results by adapting diverse synthetic datasets [38]. However, further research is warranted to establish a comprehensive correspondence between the biomechanical parameters of vocal folds and their respective vibrational modes.
The sequential exploration of potential values to achieve optimal results, which effectively traverses the search space, proves to be invaluable in addressing complex issues such as tuning a vocal production model. Although the results obtained through this technique are deemed adequate, refinement could be achieved by incorporating clinical measurements as a reference, given that the desired conditions were predominantly derived from existing literature [54].
The performance of the tuning methodology utilizing metaheuristic methods was deemed adequate in attaining the desired behavior, with consistent results. However, it is imperative to underscore that the tuning conditions could be further refined by giving greater weight to clinical measurements as a reference point, enabling the algorithm to emulate a vocal system behavior that more closely mirrors natural or clinically established parameters [55].
Finally, the proposed technique lays the foundation for potential extensions to include a wider array of search algorithms, with the aim of enhancing error conditions and streamlining processing resources.
Limitations and Future Directions
The parametric approach utilized, while robust, may not encapsulate the entirety of complexity and variability in vocal production, particularly in clinical scenarios. Additionally, while extensive efforts were made in tuning, other biomechanical and physiological factors may influence vocal fold behavior that were not accounted for in this model. Furthermore, the results are based on data from a male speaker, which may limit their generalizability to other genders or vocal profiles. Future research should aim to address variability in vocal production among different populations, including female speakers and individuals with diverse vocal characteristics.
Moving forward, exploring multi-objective approaches and integrating machine learning techniques may further enhance the precision and clinical applicability of biomechanical vocal fold models. Additionally, incorporating clinical data and direct measurements into the parametric tuning process could provide a more robust and specific foundation for assessing patients with vocal disorders. Expanding this approach to three-dimensional models and considering more complex interactions between vocal folds and other components of the vocal tract may offer a more comprehensive and accurate representation of vocal production in clinical contexts. Furthermore, experimental validation of the results through clinical trials and comparisons with direct clinical measurements would be crucial to confirm the utility and accuracy of this approach in diagnostic and treatment contexts for vocal disorders. This research avenue holds promise for advancing clinical practice in the field of phonation and voice, enabling a more personalized and effective approach to treating patients with vocal disorders.
Conclusion
This study highlights the effectiveness of metaheuristic methods in the parametric adjustment of vocal production modeling. The fine-tuned model achieves an accurate reproduction of vocal fold behavior, allowing for precise estimation of impact stress during phonation. The results demonstrate a significant improvement in vocal behavior representation, affirming the utility of this methodology. Despite the potential for further improvement through clinical measurements, this approach establishes a solid foundation for future research in vocal biomechanics. Multi-objective optimization, the integration of machine learning techniques, and the investigation of complex vocal fold interactions present exciting avenues for future exploration. Experimental validation and clinical comparison will further enhance the practical utility of the method. This study constitutes a significant step towards more precise vocal modeling and its clinical application.