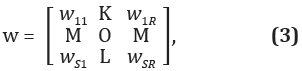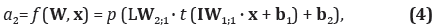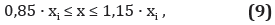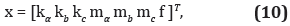CALIBRACIÓN DE LOS PARÁMETROS DE UN MODELO DE HORNO DE ARCO ELÉCTRICO EMPLEANDO SIMULACIÓN Y REDES NEURONALES

CALIBRATION OF PARAMETERS FOR ELECTRIC ARC FURNACE MODEL USING SIMULATION AND NEURAL NETWORKS

CALIBRAÇÃO DE PARÂMETROS DE UM MODELO USANDO FORNO DE ARCO ELÉTRICO EMPREGANDO SIMULAÇÃO E REDES NEURAIS

Mauricio Alexánder Álvarez López¹, Carlos Alberto Henao Baena², Jesser James Marulanda Durango³

1 Ingeniero eléctrico. Magíster en Ingeniería Eléctrica. PhD. Computer Science. Profesor Asociado, Universidad Tecnológica de Pereira. Carrera 27 N. 10-02, Pereira (Colombia). Tel: (576) 313 73 00. Correo electrónico: malvarez@utp.edu.co.
2 Ingeniero eléctrico. Magíster en Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Pereira, Colombia.
3 Ingeniero electrico. Magíster en Ingeniería Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia.

Artículo recibido: 8-IV-2013 / Aprobado: 27-III-2014
Disponible online: 30 de agosto de 2014
Discusión abierta hasta diciembre de 2015

RESUMEN

El horno de arco eléctrico proporciona un medio relativamente simple para la fusión de metales. Se utiliza en la producción de acero de alta pureza, aluminio, cobre, plomo, entre otros metales. Sin embargo, los hornos de arco son considerados como la carga más nociva para el sistema eléctrico de potencia. Por consiguiente, resulta de gran importancia contar con modelos de horno de arco que permitan determinar con alto grado de aproximación el comportamiento de este tipo de carga, puesto que se podría evaluar su impacto en términos de índices de calidad de energía para el sistema de potencia al cual se conecten. Uno de los principales problemas que surge al utilizar los modelos matemáticos de arco eléctrico consiste en la calibración de los parámetros que describen la dinámica del modelo. En este documento se muestra un procedimiento para calibrar todos los parámetros de un modelo de horno de arco eléctrico de corriente alterna, dadas mediciones reales de tensiones y corrientes. Se utiliza una red neuronal multicapa como emulador del modelo del horno. La red neuronal se entrena empleando datos de simulación obtenidos del modelo del horno implementado en el entorno Matlab®-Simulink®. Una vez entrenada la red, los parámetros de interés se obtienen resolviendo un problema inverso. Los resultados obtenidos muestran un error máximo de 4,1 % en el valor eficaz de las corrientes del arco eléctrico.

PALABRAS CLAVES: horno de arco; calibración de parámetros; redes neuronales; Latin Hypercube; emulación por computador.

ABSTRACT

Electric arc furnace provides a relatively simple way for melting metals. They are used in the production of highly purified steel, aluminium, copper and other metals. However, they are considered the more damaging load for the power system. It is very important, therefore, to count on arc furnace models for determining with high degree of accuracy the performance of this type of load. In this way, it would be possible to assess the impact in terms of power quality indices for the power system to which they might be connected. When using electric arc furnace models in practice, a key issue is the calibration of the parameters of the model. In this paper, we show a procedure for calibrating all the parameters of an AC electric arc furnace model using real measurements of voltages and currents. It uses a multilayer neural network as an emulator of the electric arc furnace model. The neural network is trained using data obtained from the simulation of the electric arc furnace model implemented in Matlab®-Simulink®. Once the network is trained, the parameters of interest are obtained by solving an inverse problem. Results obtained show a maximum percentage error of 4.1 % for the rms value of the current involved in the electrical arc.

KEY WORDS: Electric Arc Furnace; Calibration of Parameters; Neural Networks; Latin Hypercube; Computer Emulation.

RESUMO

O forno a arco elétrico fornece um meio relativamente simples para a fusão de metais. Ele é usado na produção de ferro de alta pureza, alumínio, cobre, chumbo, e outros metais. No entanto, os fornos a arco são considerados a carga mais prejudicial no sistema elétrico de potência. Por conseguinte, é muito importante dispor de modelos de forno de arco para determinar com um elevado grau de aproximação o comportamento deste tipo de carga, uma vez que poderia avaliar o seu impacto em termos de índices de qualidade de energia para o sistema potencial para o que eles se conectam. Um dos principais problemas que surgem quando se utiliza modelos matemáticos do arco elétrico é a calibração dos parâmetros que descrevem dinâmica do modelo. Este documento apresenta um método para calibrar todos os parâmetros de um modelo de forno de arco elétrico de tensao alterna, dadas as medidas reais de tensões e correntes. Utiliza-se uma rede neural de multicamadas com um emulador de modelo de forno. A rede neural é treinada usando dados de simulação obtidos do modelo de forno usado no ambiente Matlab®-Simulink®. Uma vez seja treinada a rede, os parâmetros de interesse são obtidos através da resolução de um problema inverso. Os resultados obtidos mostram um erro máximo de 4,1 % no valor eficaz correntes de arco elétrico.

PALAVRAS-CHAVE: Fornos de arco; Calibração de parâmetros; Redes neurais; Latin Hypercube; Emulação de computador.

1. INTRODUCCIÓN

El incremento de instalaciones eléctricas que cuentan entre sus cargas con hornos de arco eléctrico, ha venido generando gran interés en las empresas de distribución de energía debido a que esta carga se considera como la más nociva para el sistema eléctrico de potencia en cuanto a la calidad de potencia se refiere.

En general, el funcionamiento del horno de arco se divide en las fases de fusión y afino. En la etapa de fusión, piezas del material a fundir cortocircuitan continuamente los electrodos del horno ocasionando variaciones en la impedancia equivalente del circuito eléctrico de los electrodos y en consecuencia fluctuaciones aleatorias en las corrientes del circuito. Los efectos continúan y ahora las fluctuaciones de corriente conllevan a variaciones en la potencia reactiva y caídas momentáneas de voltaje ( flicker) en el barraje de conexión de la carga y en otros barrajes cercanos. En la etapa afino o refinado las variaciones de la impedancia del circuito disminuyen causando un menor impacto en el sistema de potencia. Los hornos de arco eléctrico también son conocidos por ser fuentes de armónicos, estableciendo condiciones indeseables de operación en los elementos conectados a la red eléctrica.

Por lo tanto, poder modelar el comportamiento de un horno de arco eléctrico cobra gran importancia para las compañías de distribución (entre otras), en cuanto les permitiría contar con una herramienta computacional para conocer el impacto que podría generar en el sistema de potencia o para diseñar sistemas de compensación como el compensador estático síncrono (D-StatCom, acrónimo de sus siglas en inglés static synchronous condenser) o el compensador estático de potencia reactiva (SVC), García Cerrada, et al., 2000).

Sin embargo, uno de los grandes problemas que surge en la práctica al momento de utilizar uno de estos modelos de horno de arco consiste en la calibración de sus parámetros. En la literatura se muestran artículos donde los parámetros se sintonizan de forma heurística, con base en mediciones reales del índice de severidad de flicker de corta duración (Pst), o con base en las potencias nominales del horno. En Collantes-Bellido y Gómez-SanRomán (1997) se presenta una metodología para estimar los parámetros a partir de mediciones reales de voltaje, usando el toolbox System Identification de Matlab®. En Alves, et al. (2010) se ajustan los parámetros para estimar el Pst de una nueva instalación con base en un análisis estadístico de mediciones reales de Pst de instalaciones similares. Un criterio para estimar el rango de variación de la resistencia del arco eléctrico se presenta en Horton, et al. (2009), con base en curvas que relacionan el factor de potencia de la instalación en función de la resistencia del arco y considerando valores típicos que toma el factor de potencia real en este tipo de instalaciones. Para su funcionamiento, estos métodos de calibración de parámetros se basan en modelos soportados en datos, que necesitan de una cantidad masiva de mediciones reales de la planta para la correcta calibración.

En Marulanda-Durango, Sepúlveda-Londoño, y Álvarez-López (2012) se estiman algunos de los parámetros del modelo de horno de arco presentado en Alzate-Gómez, Marulanda-Durango y Escobar- Mejía (2010) usando una de las técnicas de estimación de parámetros clásica más empleada en la práctica: la estimación por máxima verosimilitud (Máximum Likelihood Estimation -MLE). Sin embargo, esta metodología requiere transformar la ecuación diferencial no lineal que modela el arco eléctrico (Acha, Semlyen y Rajakovic, 1990) en una ecuación lineal equivalente en los parámetros del modelo a estimar, y solo permite la estimación de un subconjunto de los parámetros del modelo mencionado.

En este documento se propone y evalúa una metodología basada en redes neuronales para calibrar los parámetros del modelo de horno de arco trifásico propuesto en Alzate-Gómez, Marulanda-Durango y Escobar-Mejía (2010). Este modelo fue implementado en el entorno Matlab®-Simulink®, y se utilizó para generar una gran cantidad de formas de onda de voltajes y corrientes de arco eléctrico, usando en cada simulación diferentes valores para los parámetros del modelo. Los valores de los parámetros en cada simulación se obtuvieron usando muestreo por hipercubo latino (Latin Hypercube Sampling) (Wyss y Jorgensen, 1998). Los datos de la simulación se emplearon para entrenar una red neuronal multicapa, cuya función es servir como emulador determinístico del modelo dinámico. Una vez entrenada la red neuronal, la calibración de los parámetros se realiza resolviendo un problema inverso, en el que se conocen los voltajes y corrientes (reales), pero se desconocen los parámetros del modelo que generaron dichas señales. La validación de los resultados obtenidos se realiza comparando los valores eficaces de las señales reales y las señales simuladas con los parámetros obtenidos a través de la solución del problema inverso.

El artículo está organizado de la siguiente forma: en la sección 2 se presenta una descripción del modelo del horno de arco, la red neuronal utilizada, el algoritmo Backpropagation (de propagación hacia atrás) y el método para el muestreo de datos. En la sección 3 se describe la metodología utilizada para generar los datos de entrenamiento de la red neuronal y realizar su inversión. Por último, se muestran los resultados obtenidos y se presentan las conclusiones de la investigación.

2. MARCO TEÓRICO

En esta sección se presenta el modelo del horno de arco trifásico y se describen las redes neuronales junto al algoritmo Backpropagation. Adicionalmente, se describe el problema inverso y el método latin hypercube para el muestreo de datos.

2.1. Modelo matemático de un horno de arco eléctrico trifásico

El modelo de horno de arco que se utiliza para estimar sus parámetros se presenta en Marulanda-Durango, Sepúlveda-Londoño y Álvarez-López (2012), por lo cual, en este documento se hará una corta descripción del mismo. El modelo se divide en dos partes: inicialmente se modela la característica no lineal voltaje-corriente típica de un arco eléctrico y luego se considera la naturaleza variable de la longitud del arco modulando en amplitud el radio del arco con tres señales de baja frecuencia: una señal sinusoidal, una señal de naturaleza caótica y una señal aleatoria con distribución de probabilidad Gaussiana; esto con el fin de asemejar las fluctuaciones que se observan en las formas de onda reales de voltajes y corrientes de un horno de arco eléctrico. La característica no lineal voltaje-corriente de un arco eléctrico se obtiene solucionando la siguiente ecuación diferencial (Acha, et al., 1990)

donde r es el radio del arco eléctrico, i es la corriente instantánea del arco y k₁, k₂ y k₃ son parámetros que se relacionan con la potencia eléctrica convertida en calor por el arco. En la Figura 1 se muestra en diagrama de bloques la forma de obtener r tomando como entrada la corriente i.

En el modelo trifásico del horno de arco se debe obtener para cada corriente de línea su respectivo valor de r. Una vez determinado r (por fase), la segunda parte del modelo determina el voltaje dinámico del arco eléctrico. Para esto, previamente se realiza la modulación de amplitud de r con las tres señales, es decir, la señal sinusoidal, la señal de naturaleza caótica, y la señal aleatoria con distribución gaussiana. En la Figura 2 se ilustra la implementación en diagrama de bloques de la segunda fase del modelo. Donde c es una señal caótica de baja frecuencia generada con el oscilador de Chua (Kennedy, 1993), y g es una señal aleatoria que tiene una distribución de probabilidad gaussiana (Manchur, 1992). Las constantes A, B y C representan los índices de modulación de amplitud para las tres señales moduladoras. Una vez obtenido r_d, el voltaje dinámico del arco eléctrico por fase, se determina con la siguiente ecuación,

Se ha utilizado una topología típica para el circuito eléctrico que alimenta el horno de arco (Montanari, et al., 1994). En la Figura 3 se muestra el diagrama unifilar del circuito indicando los valores utilizados para sus componentes.

En resumen, los parámetros del modelo del horno de arco que se desean sintonizar usando una red neuronal son k₁, k₂, k₃, A, B, C y f por cada fase, en total 21 parámetros.

2.2. Red neuronal

Las redes neuronales artificiales son sistemas paralelos para el aprendizaje y procesamiento automático de información, emulando la forma en que funcionan las redes de neuronas biológicas del cerebro humano.

2.2.1. Representación de la red neuronal

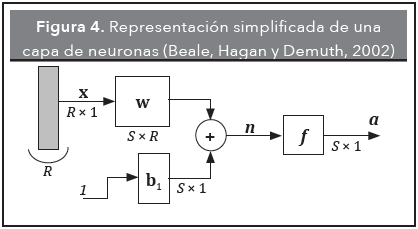
Las redes neuronales tratadas en la mayoría de las aplicaciones poseen la característica de estar organizadas por capas y ser redes totalmente interconectadas (Hilera-González y Tome-García, 1995; Rumelhart, et al., 1986). Lo anterior hace posible crear un tipo de notación gráfica simplificada, en la cual, no se muestran explícitamente las neuronas sino más bien las capas de la red como elementos de bloques constructivos (Quintero-Osorio, 2004). Para el caso de una capa de neuronas, la notación gráfica simplificada es la que se muestra en la Figura 4 (Beale, Hagan y Demuth, 2002).

Debido a la conexión total de las señales de entrada xi con las respectivas neuronas, el número de pesos sinápticos de cada neurona es igual (en dimensión) y por lo tanto, es posible agrupar dichos pesos en una matriz W denominada matriz de pesos sinápticos.

Cabe anotar que, si una entrada no está conectada con una determinada neurona la notación matricial todavía es consistente con la condición que el peso correspondiente de dicha conexión es igual a cero. Aun más, en la mayoría de las aplicaciones la función de activación de las capa de entrada y de las capas ocultas es igual para todas las neuronas de la respectiva capa y por lo tanto, pueden unificarse en un único bloque función denominado f. Los pesos sinápticos de una determinada neurona con las respectivas entradas xi de la capa se pueden ver como un vector fila y por lo tanto, todos los pesos de una capa se pueden representar por una matriz de pesos W.

donde S es el número de neuronas de la respectiva capa y R es el número de entradas (escalares) a la capa. Además de crear una notación más estructural y generalizada, la notación matricial se aplica para hacer distinción entre las matrices de pesos sinápticos de la capa de entrada y las conexiones entre capas intermedias con las demás capas (ocultas, salida). Adicionalmente se utiliza para indicar el inicio y el destino de la conexión entre capas. A modo de ejemplo, la notación IW_1;1 es la matriz de pesos sinápticos de la capa de entrada de la red neuronal y LW_2;1 es la matriz de pesos sinápticos que conecta la segunda capa de la red con la primera. Esta notación se ilustra en la Figura 5 (Beale, Hagan y Demuth, 2002).

De acuerdo con la anterior figura, el modelo matemático de la función de salida a₂ de la red neuronal es el que se describe en la siguiente ecuación:

donde p(z) es la función de activación lineal definida como purelin(z) = z; y t(z) es la función de activación tangente hiperbólica definida como (Demuth y Beale, 2002).

2.3. El algoritmo Backpropagation

El algoritmo de propagación hacia atrás o backpropagation (de su traducción al inglés) es una regla clásica de entrenamiento de redes neuronales con más de una capa oculta (Rumelhart, et al., 1986). La idea básica del entrenamiento de una red neuronal consiste en encontrar los parámetros IW, LW, b₁ y b₂, que mejor ajusten un conjunto de datos de entrada y salida.

El entrenamiento de la red backpropagation consta de un ciclo de propagación de dos fases. Inicialmente, se aplica un ejemplo de entrada como estímulo para la capa de neuronas de entrada de la red, el cual, se va propagando a las demás capas de la arquitectura de la red (capas ocultas), generando una respuesta en la capa de salida de la red; luego se comparan las respuestas obtenidas en las neuronas de la capa de salida con la salida deseada, es decir, con el patrón de salida que corresponde al estímulo de entrada. Para finalizar la primera fase se calcula un error para cada una de las neuronas de la capa de salida.

La segunda fase del algoritmo consiste en propagar el error calculado en la fase inicial desde de la capa de salida hacia todas las neuronas de las capas ocultas que contribuyen directamente con la salida. A estas capas intermedias se les asigna un porcentaje del error en función del aporte de estas neuronas intermedias en la salida obtenida en la fase 1. Este proceso se repite en todas las capas de la red, hasta que a todas las neuronas de la misma se les asigne un error que describa su aporte relativo al error total de salida. En función del error recibido se modifican los pesos sinápticos de cada neurona de la red. Se espera que al presentarse un estímulo de entrada conocido la respuesta de la red coincida con la salida deseada (Hilera-González y Tome-García, 1995).

2.4. El problema de inversión de redes Feedforward

Una red neuronal entrenada puede considerarse como un mapeo no lineal desde el espacio de entrada al espacio de salida (Bao, et al., 1999). Una vez la red neuronal ha sido entrenada sobre el conjunto de datos de entrenamiento, todos los pesos sinápticos -incluyendo los bias- de la red permanecen fijos. Así, la asignación del espacio de entrada con el espacio de salida es conocido. Esta asignación se conoce como mapeo hacia adelante. En general, la correlación del mapeo hacia adelante es una relación de varios a uno, porque cada una de las salidas deseadas puede corresponder a varias entradas diferentes de entrenamiento. Se expresa el mapeo hacia adelante de la siguiente manera

donde y = [y₁, y₂,..., y_m]^T y x = [x₁, x₂,..., x_R]^T representan las salidas y las respectivas entradas de la red, W denota la matriz de pesos sinápticos fijados en el proceso de entrenamiento y la función f denota el mapeo hacia adelante definido por la arquitectura de la red. Por otro lado, el problema de inversión de una red neuronal feedforward (también conocida como red backpropagation) previamente entrenada consiste en determinar la entrada x que produce una determinada respuesta de salida d = [d₁, d₂,..., d_m]^T. Tales valores calculados de x se denominan inversiones de red o simplemente inversiones. El mapeo del espacio de salida al espacio de entrada se conoce como mapeo inverso. En los últimos años, diferentes algoritmos para invertir redes feedforward han sido propuestos. Para mayor información se sugiere consultar a Linden (1997).

2.5. Formulación del problema de inversión como un problema de optimización

Una vez realizado el entrenamiento de la red, el problema que surge ahora es encontrar la inversión de la red que produce la salida d. Para determinar diversas inversiones para una salida dada, se formula el problema inverso como un problema de optimización

donde g(x) es la función objetivo a minimizar, mientras que x_min y x_max son vectores cuyas componentes son valores constantes que representan el rango de las componentes del vector de entrada x a determinar. La función objetivo del modelo propuesto en (Jordan y Rumelhart, 1992) se describe en la siguiente ecuación

donde d es el vector de salida o validación y f es el modelo matemático que describe a la red feedforward previamente entrenada. El algoritmo de inversión de redes feedforward se puede resumir en dos pasos generalizados.

2.6. El método de muestreo latin hypercube

El método de muestreo de latin hypercube (hipercubo latino) consiste en seleccionar n valores de cada una de las k componentes del vector x = [x₁, x₂,..., x_R]^T de la siguiente forma. El rango de los posibles valores que toma cada componente del vector x se divide en m intervalos no superpuestos sobre la base de igual pro babilidad. Se selecciona al azar (random) un valor para cada uno de los m intervalos con respecto a la densidad de probabilidad. Las m muestras así obtenidas para la componente x₁ se combinan de forma aleatoria con las m muestras de la componente x₂. Estos m pares se combinan de nuevo con los m valores de la componente x₃ para formar m tripletes, de esta manera el proceso continúa hasta que se forman m k-duplas. Es conveniente pensar en estas muestras de cada una de las k componentes del vector x como la formación de una matriz, donde cada una de sus columnas contiene valores específicos (muestras) de cada una de las componentes de x, las cuales pueden ser utilizadas en un modelo computacional.

3. MATERIALES Y MÉTODOS

En esta sección se detalla la metodología empleada para la estimación de los parámetros del modelo de horno de arco eléctrico definido en la sección 2.1. Se presenta la forma de obtener los datos de entrenamiento de la red neuronal a partir del modelo; además, se introducen las herramientas computacionales nativas de Matlab® usadas para el entrenamiento y la inversión de la red neuronal.

3.1. Base de datos reales

Los datos reales que se emplean para calibrar los parámetros del modelo del horno de arco fueron usados por Cano-Plata y Tacca (2005), y constan de mediciones de los voltajes de fase en el secundario del transformador T₂ de la Figura 3, y las corrientes del arco eléctrico durante cinco (5) ciclos, con una frecuencia de muestreo de 2048 mps (mps - muestras por segundo), tomadas en la fase de fusión del horno.

3.2. Datos para el entrenamiento de la red neuronal

Según algunas pruebas realizadas, se presume que los valores de los parámetros del modelo de horno de arco que sintetizan los datos reales se encuentran en el rango

donde el vector x de dimensión [21×1] representa los parámetros del modelo que se desean calibrar, x_i es el vector de parámetros iniciales (conocido) y la desigualdad de la anterior ecuación se aplica a cada una de las componentes de los vectores x y x_i. Los parámetros del modelo trifásico del horno de arco se relacionan con los elementos del vector x de la siguiente forma

en la ecuación anterior k_a es un vector fila cuyas componentes son los parámetros k₁, k₂ y k₃ para la fase a y m_a es un vector fila donde sus componentes son los índices de modulación A, B y C para la misma fase. Una interpretación similar aplica para los otros elementos de x (k_b k_c m_b m_c). Por último, f es el vector fila cuyas componentes son las frecuencias de las tres fases f_a, f_b y f_c, como se muestra en el diagrama de bloques del modelo por fase del horno de arco de la Figura 2. Las componentes de x_i se resumen en la Tabla 1.

Tabla 1

Aplicando el método de muestreo de latin hypercube alrededor de la desigualdad que se presenta en la Ecuación 9, se generan n vectores x de entrenamiento para la red neuronal que se agrupan en las columnas de la matriz X de dimensiones [21×n], donde n es el número de ejemplos (o simulaciones) presentados a la red y 21 corresponde al número de parámetros a calibrar. Para determinar los patrones de entrenamiento de salida y de la red neuronal, resulta necesario simular el modelo del horno de arco n veces usando los vectores x, para obtener en cada simulación las formas de onda de las corrientes del arco eléctrico y los voltajes de fase en el secundario del transformador T₂ que se muestra en la Figura 3. Luego, usando la transformada corta de Fourier (Jaramillo y López-Varona, 2007) con ventanas de 20 ms y traslape de 37,5 %, se determina el espectro para cada una de las seis señales simuladas (tres de voltaje y tres de corriente), y así formar un vector de características y por cada señal. Cada uno de estos vectores se agrupa en las columnas de la matriz Y obteniendo de esta forma una matriz de dimensiones [54×n] para formar los datos de entrenamiento de salida. Por cada ventana, se obtiene la media del valor absoluto de la transformada de Fourier correspondiente, y esta media se usa como característica de salida, es decir, como parte de la matriz Y.

La aplicación de la metodología utilizada para determinar el conjunto de datos de entrenamiento entradasalida (X, Y) de la red neuronal se resume en la Figura 6.

Así se completa el conjunto de entrenamiento entrada-salida (X, Y) necesario para realizar el entrenamiento de la red neuronal. Solo resta determinar el vector de datos de validación d de dimensión [54×1], que consiste en el espectro de las formas de onda reales de los voltajes y corrientes en el secundario del transformador T₂, de la misma forma como se hizo para el entrenamiento. Las características de las señales de validación se indican en la sección 3.1.

3.3 Entrenamiento e inversión de la red neuronal

El entrenamiento de la red neuronal se realizó utilizando el toolbox Neural Network Toolbox con 500 simulaciones para construir el conjunto de entrenamiento (X, Y) para evitar un posible sobreentrenamiento. Cabe anotar que para el entrenamiento de la red neuronal se considera el horno de arco trifásico como una unidad, debido a la interrelación que existe entre las corrientes y voltajes del horno trifásico.

Una vez realizado el entrenamiento de la red neuronal, se resuelve el problema inverso aplicando las Ecuaciones 7 y 8. Así, para una red feedforward con una capa oculta con función de activación de tipo sigmoidal y una capa de salida cuya función de activación es de tipo lineal, el problema de optimización planteado en la Ecuación 7 se transforma en la siguiente ecuación

donde p es la función lineal y t es la función sigmoidal. Para la solución de la Ecuación 11 se utilizó la función fmincon que hace parte del toolbox Optimization la cual encuentra el mínimo de una función no lineal de varias variables sujeto a varias restricciones usando el método de optimización trust región reflective (Coleman y Li-Yuyin, 1996). El número de iteraciones utilizadas en el algoritmo de inversión está en función de una tolerancia de 1e-6 (si el algoritmo no converge a valor de la tolerancia en número de iteraciones del método es 1.000).

4. RESULTADOS

En esta parte del documento se presentan los resultados obtenidos de la metodología de calibración de parámetros del modelo de horno de arco eléctrico trifásico usando redes neuronales y datos reales. Además, se realiza una comparación de algunas características de las formas de onda (voltajes y corrientes) reales y sintetizadas a través del modelo.

Las pruebas realizadas consistieron en entrenar e invertir una red neuronal con una capa oculta, donde para cada experimento se modificó el número de neuronas de esta capa. En la primera prueba se utilizó una neurona para la capa oculta. Después de la fase de entrenamiento de la red neuronal se resuelve el problema inverso planteado en la Ecuación 11 para obtener los parámetros del modelo del horno de arco. Con los parámetros obtenidos para el modelo de horno de arco se realizó la simulación del mismo. Posteriormente se comparó las formas de onda reales (voltajes y corrientes) de planta con las formas de onda simuladas. Luego, el procedimiento se repite variando el número de neuronas de la capa oculta, incrementando en cada prueba 5 neuronas hasta alcanzar un máximo de 50 neuronas. Los resultados de los errores eficaces entre los datos reales y generados con el modelo para 40, 45 y 50 neuronas se enseñan en la Tabla 2.

Se aprecia en la tabla anterior que independiente de la topología de la red neuronal (número de capas ocultas y número de neuronas por capa oculta), esta emula de manera satisfactoria la dinámica no lineal del horno de arco. Si bien los experimentos se pueden realizar para diferentes configuraciones en busca de disminuir los errores porcentuales, la metodología sigue siendo válida e independiente de la arquitectura de la red neuronal.

En la Tabla 2, V_a e I_a hacen referencia al voltaje de fase en el secundario del transformador T₂ y a la corriente del arco eléctrico para la fase a, respectivamente; de igual forma para las tensiones y corrientes restantes. Por otro lado, el cálculo del porcentaje de error se obtiene a partir de la siguiente ecuación:

donde 'valor real' hace referencia al valor eficaz de la señal real, mientras que 'valor medido' hace referencia al valor eficaz de las señales obtenidas aplicando la metodología. En la siguiente tabla se muestran los valores obtenidos para las componentes del vector x luego de resolver el problema de optimización planteado en la Ecuación 11 usando 45 neuronas para la capa oculta.

Figura 7

Con base en los resultados de la tabla anterior, se realizó la simulación del modelo del horno de arco, evidenciando en esta que tales parámetros no afectan la estabilidad del circuito eléctrico de la Figura 3. Una gráfica comparativa de las señales reales y simuladas para los voltajes de fase se muestra en la siguiente figura en un intervalo de tiempo de 0,12 segundos. Las señales reales corresponden a las ondas con trazo continuo y las señales simuladas se han graficado con líneas punteadas.

En esta figura se observa que el modelo del horno de arco captura la naturaleza no lineal de los voltajes reales; además, los valores de las componentes del vector de parámetros obtenidos con el algoritmo, permiten obtener niveles de voltaje similares a los reales. El porcentaje de error obtenido para los voltajes de fase fue de 1,17 % para la fase a, 2,79 % para la fase b y 2,94 % para la fase c.

En la Figura 8 se muestran las corrientes instantáneas del arco eléctrico reales y simuladas en cada una de las fases en un tiempo de 0,12 segundos.

Figura 8

En la anterior figura, se observa que las corrientes simuladas siguen con alto grado de precisión a las corrientes reales en algunos ciclos, en los demás ciclos las corrientes se alejan en los extremos positivos y negativos. El porcentaje de error que se obtuvo para las corrientes del arco eléctrico fue de 0,88 % para la fase a, 0,08 % para la fase b y 4,1 % para la fase c.

5. CONCLUSIONES

Con base en los resultados obtenidos, se puede concluir que la inversión de una red neuronal aplicada a la sintonización de los parámetros del modelo de horno de arco entrega resultados aproximados a los datos reales de planta. Se debe tener cuidado con la respectiva configuración de la red (número de capas y número de neuronas por capa), debido a la fuerte dependencia de esta con los errores calculados de las tensiones y corrientes de arco eléctrico.

Según los resultados obtenidos, la metodología implementada en la presente investigación permite representar con alta fidelidad las formas de onda de las señales de tensión por fase de un hornode arco eléctrico real. Adicionalmente, se obtiene un error porcentual máximo de 4.1 % en el valor eficaz de las corrientes del arco eléctrico respecto a las señales reales. Por último, cabe mencionar que el modelo aproxima mejor las formas de onda de las señales de voltaje que las de corriente, debido a la menor fluctuación que tienen las señales de voltaje respecto a las fuertes variaciones que se evidencian en las ondas de corriente.

REFERENCIAS

Acha, E.; Semlyen, A.; Rajakovic, N. (1990). A Harmonic Domain Computational Package for Nonlinear Problems and its Application to Electric Arcs. IEEE Transactions on Power Delivery, 5(3), pp. 1390-1397.         [ Links ]

Alves, M.F.; Assis, Z.M.; García, C.P.; Gomes, D.G. (2010). An Integrated model for the Study of Flicker Compensation in Electrical Networks. Electric Power System Research, 80(10), pp. 1299-1305.         [ Links ]

Alzate-Gómez, A.; Marulanda-Durango, J.J.; Escobar-Mejía, A. (2010). Electric Arc Furnace Modeling for Power Quality Analysis, Bogota, Presented at IEEE ANDESCON, 15-17 Septiembre, pp. 1-6.         [ Links ]

Cano-Plata, E.A.; Tacca, H.E. (2005). Arc Furnace Modeling in ATP-EMTP. Presented at the International Conference on Power System Transients, Montreal Canada. pp. 19-23.         [ Links ]

Coleman, T.F.; Li, Yuyin. (1996). An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM Journal on Optimization, 6(2), pp. 418-445.         [ Links ]

Collantes-Bellido, R.; Gómez-SanRomán, T. (1997). Identification and Modelling of a Three Phase arc Furnace for Voltage Disturbance Simulation. IEEE Transactions on Power Delivery, 12(4), pp. 1812-1817.         [ Links ]

Beale, M.H.; Hagan, M.T.; Demuth, H. B. (2002). Neural Network Toolbox For Use with MATLAB. User's Guide. The MathWorks Inc.: 3 Apple Hill Drive. Natick, MA 01760-2098.         [ Links ]

García-Cerrada, A.; García-González, P.; Collantes-Bellido, R.; Gómez-SanRomán, T.; Anzola, J. (2000). Comparison of Thyristor Controlled Reactors and Voltaage-Source Inverters for Compensation of Flicker Caused by Arc Furnaces. IEEE Transactions on Power Delivery, 15(4), pp. 1225-1231.         [ Links ]

Hilera-González, J.R.; Tome-García, A. (1995). Redes neuronales artificiales. Fundamentos, modelos y aplicaciones. 108478971556th ed. RA-MA S.A. Editorial y Publicaciones.         [ Links ]

Horton, R.; Haskew, T.A.; Burch, R.F. (2009). A Time-Domain Ac Electric Arc Furnace Model for Flicker Planning Studies. IEEE Transactions On Power Delivery, 24(3), pp. 1450-1457.         [ Links ]

Jaramillo, A.; López-Varona, R. (2007). Transformada corta de Fourier. Scientia et Technica, 13(34), mayo, pp. 519-521.         [ Links ]

Jordan, M.I.; Rumelhart, D.E. (1992). Forward Models: Supervised Learning with a Distal Teacher. Cognitive Science, 16(3), pp. 307-354.         [ Links ]

Kennedy, M.P. (1993). Three Steps to Chaos-Part I: Evolution. IEEE Transactions on circuit and systems-I: Fundamental theory and applications, 40(10), pp. 640-656.         [ Links ]

Linden, A. (1996). Iterative Inversion of Neural networks and its Applications, in Handbook of Neural Computation, M. Fiesler and R. Beale. Inst. Phys. Publishing and Oxford Univ. Press.         [ Links ]

Manchur, G. (1992). Development of a Model for Predicting Flicker from Electric Arc Furnace. IEEE Transactions on Power Delivery, 7(1), pp. 416-426.         [ Links ]

Marulanda-Durango, J.J.; Sepúlveda-Londoño, C.D.; Álvarez-López, M.A. (2012). Estimación de los parámetros de un modelo de un horno de arco eléctrico usando máxima verosimilitud. TecnoLógicas, (29), pp. 69-89.         [ Links ]

Montanari, G.C.; Loggini, M.; Cavallini, A.; Pitti, L.; Zaninelli, D. (1994). Arc Furnace Model for the Study of Flicker Compensation in Electrical Networks. IEEE Transactions on Power Delivery, 9(4), pp. 2026-2036.         [ Links ]

Ozgun, O.; Abur, A. (2002). Flicker Study Using a Novel Arc Furnace Model. IEEE Transactions on power delivery, 17(4), pp. 1158-1163.         [ Links ]

Quintero-Osorio, J.J. (2004). Herramienta para redes neuronales en tiempo real. Tesis profesional como requisito parcial para obtener el título de Ingeniero en Electrónica, Armenia, Universidad del Quindio. Disponible en: http://www.freewebs.com/jojaqui/tesis2.pdf.         [ Links ]

Rumelhart, D.E.; McClelland, J.L.; Group, P.R. (1986). Parallel Distributed Processing. Explorations in the Microstructure. Volumen I ed. Cambridge, Massachusetts, London, England: A Bradford Book.         [ Links ]

Wyss, G.D.; Jorgensen, K.H. (1998). A User's Guide to LHS: Sandia's Latin Hypercube Sampling Software. Albuquerque, NM 87185-0747: Risk Assessment and System Modeling Department. Sandia National Laboratories.         [ Links ]