Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Facultad de Ingeniería Universidad de Antioquia
versión impresa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.75 Medellín abr./jun. 2015
https://doi.org/10.17533/udea.redin.n75a06
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n75a06
Nonlinear analysis of the electroencephalogram in depth of anesthesia
Análisis no lineal de la señal de electroencefalograma en profundidad anestésica
Oscar Leonardo Mosquera-Dussan1*, Daniel Alfonso Botero-Rosas1, Mauricio Cagy2, Ruben Dario Henao-Idarraga3
1Grupo de Investigación PROSEIM, Universidad de La Sabana. Campus del Puente del Común, Km. 7, Autopista Norte de Bogotá. Apartado: 140122. Chía, Colombia.
2 Instituto Alberto Luiz Coimbra de Posgrado e Investigación en Ingeniería (COPPE), Universidad Federal de Río de Janeiro. Av. Horácio Macedo 2030, Ciudad Universitaria. C.P. 21941-914. Río de Janeiro, Brasil.
3 Departamento de Anestesia, Clínica Universidad de La Sabana. Campus del Puente del Común, Km. 7, Autopista Norte de Bogotá. Apartado: 140122. Chía, Colombia.
* Corresponding author: Oscar Leonardo Mosquera Dussan, e-mail: oscar88leonardo@gmail.com
(Received December 13, 2013; accepted February 09, 2015)
Abstract
Digital signal processing of the electroencephalogram (EEG) became important in monitoring depth of anesthesia (DoA) being used to provide a better anesthetic technique. The objective of this work was to conduct a review about nonlinear mathematical methods applied recently to the analyses of nonlinear non-stationary EEG signal. A review was conducted showing time- and frequency-domain nonlinear mathematical methods recently applied to EEG analysis: Approximate Entropy, Sample Entropy, Spectral Entropy, Permutation Entropy, Wavelet Transform, Wavelet Entropy, Bispectrum, Bicoherence and Hilbert Huang Transform. Some algorithms were implemented and tested in one EEG signal record from a patient at The Sabana University Clinic. Recently published results from different methods are discussed. Nonlinear techniques such as entropy analysis in time domain and combination with wavelet transform, and Hilbert Huang transform in frequency domain have shown promising results in classifications of depth of anesthesia stages.
Keywords: depth of anesthesia monitoring, EEG features extraction, nonlinear complexity analyses, digital signal processing
Resumen
El procesamiento digital de la señal de electroencefalograma (EEG) ha tomado importancia en el monitoreo de profundidad anestésica, contribuyendo a una mejor técnica anestésica. El objetivo es realizar una revisión de métodos matemáticos no lineales aplicados recientemente al análisis de EEG la cual presenta características no lineales y no estacionarias. Una revisión fue desarrollada abarcando métodos matemáticos no lineales en el dominio del tiempo y frecuencia, los cuales han sido aplicados recientemente al análisis de EEG: Entropía Aproximada, Entropía Muestral, Entropía Espectral, Entropía Permutada, Transformada Wavelet, Entropía Wavelet, Bispectro, Bicoherencia y Transformada Hilbert Huang. Los algoritmos implementados fueron probados en un registro EEG de un paciente en la Clínica Universidad de La Sabana. Resultados publicados en la literatura a fin del tema son discutidos. Técnicas no lineales como el análisis de entropía, y la combinación con transformadas Wavelet y Hilbert Huang en el dominio de la frecuencia han presentado resultados prometedores en clasificación de estados de profundidad anestésica.
Palabras clave: monitoreo de profundidad anestésica, extracción de patrones EEG, análisis no lineal de complejidad, procesamiento digital de señales
Introduction
General anesthesia (GA) is defined as a drug-induced loss of consciousness during which patients are not arousable, even by painful stimulation [1]. GA takes an important role in surgical procedures; an anesthetic overdose may lead to coma, drug-associated toxicities and even death. On the other hand, a light anesthetic dose may lead to the well-known event of intraoperative awareness, which can cause sleep disorders, depression, night terrors, hospitals fears, and post-traumatic stress disorder [2-4].
Electroencephalographic (EEG) measures reflect the state of the central nervous system, and it has been widely used for monitoring depth of anesthesia. Electronic EEG indexes were developed based on observation that, in general, EEG of an anesthetized patient change from high frequency low amplitude during consciousness to low frequency high amplitude when deeply anesthetized. It is also noted that, during the anesthesia process, the human consciousness weakens gradually, as well as the brain activity level. In the thermodynamic perspective, the degree of EEG chaos is reduced. Therefore, the concept of ''entropy'' is introduced into the field of EEG signal processing [5-9].
In the 90s, bispectral analysis, a type of mathematical processing commonly used in geophysics and oil prospection was used to process the EEG signal. Bispectral Index technology (BIS) was developed from a closed algorithm and suggested to monitor brain activity in answer to different combinations of anesthetics. However, the bispectral analysis parameter used by BIS is the bispectrum, which by definition reflects not only the degree of phase coupling, but also the EEG amplitude. The bicoherence represents the normalization of the bispectrum, and as such is independent of signal amplitude; therefore, it could provide a more appropriate measure of phase coupling [10, 11].
Wavelet Transform (WT) is a popular method for EEG signal analysis in the frequency domain, which provides a constant resolution for all the frequencies; the WT provides multiresolution scale, i.e. different frequencies are analyzed with different resolutions. the WT has been implemented in the depth of anesthesia monitoring with promising results [12-15]. A relative recent method called Hilbert Huang Transform has been applied to the field of signal processing [16]. This transform involves a signal decomposition based on the local characteristic of the data; therefore, it was designed specifically for analyzing data from nonlinear and non-stationary processes, which perfectly suits the characteristics of the EEG signal. Combination of the Hilbert frequency representation and the spectral entropy has been called Hilbert Huang Spectral Entropy [17]. In the present review, an EEG record with sampling frequency of 300Hz from a patient at The Sabana University Clinic, with previous informed consent, was used to test the algorithms and provide a better understanding.
Entropy analysis
Approximate Entropy: mathematically, two input parameters must be chosen to compute the approximate entropy [18] of the EEG sequence (SEEG); given the pattern length (m) and the criterion of similarity (r). Then, two different patterns are similar if the difference between corresponding measurements in the patterns is less than the criterion of similarity (Eq. 1).
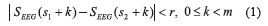
Where:
s1 is the start point for pattern 1 (pm(1));
s2 is the start point for pattern 2 (pm(2));
k is the variable that runs through the pattern.
Consider the set PM = [pm(1), pm(2), pm(3), …, pm(N-m+1)] formed by all patterns of specific length within the SEEG, then Cim(r) is defined as the fraction of patterns that resemble a specific pattern of the same length (Eq. 2).

where:
N is the length of SEEG;
nim(r) is the number of patterns in PM that are similar to pm(i).
Cim(r) is calculated for each pattern in the set PM, and Cm(r) is defined as the mean of these Cim(r) values, expressing the prevalence of repetitive patterns of length m in SEEG .
The ApEn estimates the logarithmic likelihood that the next intervals after each of the patterns will differ (Eq. 3).

Spectral Entropy: the spectral entropy (GE Healthcare Technologies, Waukesha, WI) describes the irregularity, complexity or unpredictability characteristic of a signal. The Datex-Ohmeda S/5 entropy Module (Datex-Ohmeda, Inc., Madison, WI) is of public domain [19]. The concept of spectral entropy originates from a measure of information called Shannon entropy; when applied to the power spectrum of a signal, spectral entropy is obtained. In order to calculate the spectral entropy, the Fast Fourier Transform (FFT) is considered to obtain the spectrum. Mathematically, the following steps are required to compute the spectral entropy within a particular frequency range
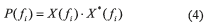
Where:
P(fi) is the power spectrum of the signal;
X(fi) is the complex frequency components of the FFT;
X*(fi) is the conjugate complex of the FFT components.
Then, the power spectrum is normalized (Eq. 5) so that the sum of the normalized power spectrum over the selected frequency region

The Shannon function is applied to calculate the spectral entropy corresponding to the frequency range
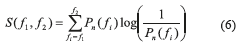
Thereafter, the entropy value is normalized (Eq. 7) to range between 1 (maximum irregularity) and 0 (complete regularity). An algorithm for spectral entropy was implemented in Matlab, Figure 1 illustrates the process described before.

Where:
SN (f1,f2) is the Normalized Spectral Entropy;
S(f1,f2) is the Spectral Entropy;
N(f1,f2) is the number of frequency components between f1 and f2.
In real time, signals are analyzed within a finite time window (epoch) of a selected length; the time window is moved step by step to provide updated estimates of the spectrum. In order to optimize the tradeoff between time and frequency resolution, the Entropy Module considers a set of window lengths chosen in such a manner that each frequency component is obtained from a time window that is optimal for that particular frequency. Hence, information is extracted from the signal as fast as possible [19].
Response Entropy and State Entropy: the spectral entropy implemented in the M-entropy module is a combined analysis of EEG and EMG signals. Two spectral entropy indexes are calculated (Figure 2): (1) State Entropy (SE), computed over the frequency range
SE primarily reflects the cortical state of the patient, and RE is useful as an indicator of frontal EMG activity. Sudden appearance of EMG signal data often indicates that the patient is responding to some external stimulus, such as a painful stimulus (i.e. nociception) due to some surgical event. Such a response may result if the level of analgesia is insufficient. If stimulation continues and no additional analgesic drugs are administered, it is highly likely that the level of hypnosis eventually starts to lighten. EMG can thus provide a rapid indication of impending arousal.
Permutation Entropy: Permutation Entropy (PE) was introduced as a complexity parameter for time series based on comparison of neighboring values; the advantages are its simplicity, extremely fast calculation and robustness [20]. The algorithm to compute the PE can be divided into four basic steps [21]:
1. Fragment the continuous EEG signal into segments containing m samples (m is called the embedding dimension); for a given embedding dimension m = 3 there will be m! Possible permutations called motifs, so in this case six different motifs are obtained.
2. Identify each motif as belonging to one of the six different categories.
3. Obtain the probability of occurrence of each motif in the signal (pi) by counting the number of motifs of each of the six different categories.
4. Apply the standard Shannon uncertainty formula to calculate the PE of the resultant normalized probability distribution of the motifs (Eq. 8):

Frequency-domain analysis
Wavelet Transform: A wave is an oscillating function of time or space and is periodic. In contrast, wavelets are localized waves. They have their energy concentrated in time or space and are suited to analysis of transient signals. While Fourier Transform uses waves to analyze signals, the Wavelet Transform (WT) uses wavelets of finite energy. In general, the signal to be analyzed is multiplied with a wavelet function, and then the transform is computed for each segment generated. The width of the wavelet function changes with each spectral component. The Continuous Wavelet Transform (CWT) is provided in equation 9.

where
x(t) is the signal to be analyzed;
j(t) is the mother wavelet or basis function;
s if the inverse of frequency or the scaling parameter;
t is the translation parameter.
All the wavelet functions used in the transformation are derived from the basis function through translation (shifting) and scaling (dilation or compression). The translation parameter relates to the location of the wavelet function as it is shifted through the signal, corresponding to time information, while the scale parameter corresponds to frequency information. Scaling either dilates or compresses a signal. Large scales (low frequencies) dilate the signal and provide global information hidden in the signal, while small scales (high frequencies) compress the signal and provide detailed information about the signal. In the case of DWT, a time-scale representation of the digital signal is obtained using digital filtering techniques. The signal is passed through filters with different cutoff frequencies at different scales. The resolution is determined by the filtering operations and the scale by upsampling and downsampling operations (Figure 3). The Mallat algorithm [22] computes the DWT by successive lowpass and highpass filters applied to the discrete time domain signal.
Hilbert Huang Transform: Hilbert Huang Transform (HHT) is the NASA´s designated name for the combination of Empirical Mode Decomposition (EMD) and the Hilbert spectral analysis (HSA). The decomposition is based on the local characteristic time scale of the data. Therefore, it was designed specifically for analyzing data from nonlinear and non-stationary processes. A clear example is the EEG signal analysis. When EMD is applied to a signal, any complicated data set can be decomposed into a finite number of components, called Intrinsic Mode Functions (IMF), defined as any function having the same (or differing at most by one) numbers of zero crossing and extrema, and also having symmetric envelopes defined by the local maxima and minima. With the Hilbert Transform (HT), the IMF's provides instantaneous frequencies as a function of time. The final representation of the result is an energy-frequency-time distribution, called the Hilbert Spectrum (Figure 4).
Empirical Mode Decomposition: HHT is based on an empirical approach; the first part is the decomposition of the analyzing signal into IMF's. An IMF is defined as a function that satisfies the following requirements:
1. In the whole data set, the number of extrema and the number of zero-crossings must either be equal or differ at most by one.
2. At any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero.
Note that, instead of constant amplitude and frequency in a simple harmonic component, an IMF can have variable amplitude and frequency along the time axis, which is usefull for nonlinear nonstationary EEG analysis. The EMD decomposing process begins with the calculation of the upper and lower envelopes. For the upper envelope all the local maxima are connected by a cubic spline. The procedure is repeated for the local minima to obtain the lower envelope. The envelopes mean are taken and are observed in Figure 5. The first component is defined as (Eq. 10):

Where
x(t) is the signal;
m1 is the mean of the upper and lower envelopes;
h1 is the first component.
The first component (h1) is treated as a proto-IMF, and it follows the sifting process up to k times. For each sifting step, the resulting component is the next corresponding data (Eq. 11):

The sifting process will stop only if for S consecutive times the numbers of zero-crossings and extrema stay the same, and are equal or at most differ by one, the first IMF component is presented in equation 12.

The first IMF should contain the finest scale or the shortest period component of the signal; in the next step, IMF is separated from the rest of the data and a residue is obtained (Eq. 13).

Then the residue is treated as the new data and submitted to the same sifting process described before. The sifting process stops finally when the residue becomes a monotonic function from which no more IMF can be extracted, finally the EMD of a signal x(t) is presented as equation 14.

The instantaneous amplitude (a) and the instantaneous frequency (w) can be computed using the Hilbert Transform (Eq. 15). A complex analytic function is defined taking the original signal (IMF) as the real part, and the imaginary part is the principal Cauchy value (denoted by P) of the improper integral in equation 16. The equation 17 shows the relationship between polar and rectangular form.

Where,


Bispectrum and Bicoherence
Bispectrum: Based on the Fourier transform; it quantifies the relationship between the underlying sinusoidal components of the EEG. Specifically, biespectral analysis examines the relationship between the sinusoids at two primary frequencies, f1 and f2, and a modulation component at the frequency f1+f2. This set of three frequency components is known as a triplet (f1, f2 and f1+f2). Calculation of the bispectrum begins with an FFT to generate complex spectral values, X(f). For each possible triplet, the complex conjugate of the spectral value at the modulation frequency is multiplied against the spectral value of the primary frequencies of the triplet (Eq. 18):

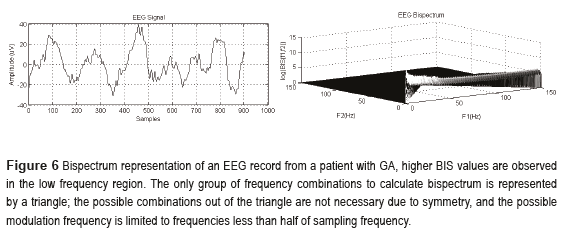
If there is large spectral magnitude at each frequency in the triplet, and if the phase angles are aligned, then the product will be large; if one of the sinusoidal components is small or absent or if the phase angles are not aligned, the product will be small. An example is illustrated in Figure 6:
The bispectrum incorporates both phase and power information; it can be decomposed to separate the magnitude of the members of the triplet, as the real triple product (Eq. 19), and the phase information, as the bicoherence (Eq. 20).


A high bicoherence value indicates that there is a phase coupling within the triplet. Strong phase coupling implies that the sinusoidal components at f1 and f2 may have a common generator, or that the neural circuit they drive may, through some nonlinear interaction, synthesize a new dependent component at the modulation frequency [23].
BIS index uses a parameter called SynchFastSlow derived from bispectral analysis. Which is the logarithmic relation between the sum of all bispectrum peaks in bands from 0.5 to 47 Hz and 40 to 47 Hz. BIS number is obtained from weighted analysis of four sub parameter: burst suppression ratio, QUAZI suppression, beta relative power and fast/slow synchronization [24]. A comparison study with clinical assessment of level of sedation show that EEG-based monitors cannot reliably distinguish between light and deep sedation [25].
Discussion
It has been suggested that entropy measures correctly classify the depth of anesthesia. The use of PE and ApEn to classify between 'awake' and 'anesthetized' state from the EEG of patients recovering from general anesthesia has been investigated [8]. Entropy measures were estimated over 2-s non-overlapping windows; for PE the embedding dimension was m=3 and the parameters r and m were set as 0.1 and 2, respectively, to calculate ApEn. Results show that there is no significant difference between linear and nonlinear support vector machine classification, which implies that both measures provide linearly separable features and mean classification accuracy greater than 96%. Thus the authors conclude that there is no need for a complex nonlinear classifier to be used. PE and ApEn show similar high performance, although ApEn is more computationally complex and its estimation takes longer than PE.
In a comparison study [5], the following entropy methods: spectral entropy, approximate entropy, sample entropy and permutation entropy, were used to track changes from continuous EEG to burst suppression in a surrogate analysis from a 40-years old male patient to test the sensitivity of measures to phase randomization and amplitude adjusting. Entropy measures were calculated in a moving window of length 4s and the step size was 1s, m=2, r=0.2SD (Standard deviation over the whole signal and it was also calculated over the segment). The symbol length parameter was set to 4 in the calculation of PE; it was highly sensitive to phase information and nonlinearities. Another comparison study of nonlinear features shows that with deepening of anesthesia degree, approximate entropy, Shannon entropy, and Lempel-Ziv complexity from EEG signal decrease gradually [6].
The introduction of nonlinear Entropy provided a new perspective to EEG analysis. Several techniques such as Artificial Neural Networks, logistic regression and support vector machine could be used to develop a model for anesthesia monitoring for classification of anesthesia depth level.
In a frequency domain, the degree of phase coupling between different spectral components has been studied as a marker of nonlinear EEG generators and is claimed to be an important aspect of BIS technology (Aspect Medical, USA). A study done by [10] evaluates the performance of the BIS and the bicoherence (BIC), since BIC is the most direct measure of phase coupling not affected by the components amplitudes, in order to analyze the interactions between frequency bands, the bifrequency plane was divided into regions. The biggest changes in the bicoherence values across depth of anesthesia states (10 states were clinically defined) occurred in the lower bifrequency regions (delta and theta). These results coincide with other works [11]. The ability to track graded changes in levels of anesthesia was significantly smaller than that obtained by BIS values, which indicates that the use of only Bicoherence parameters of any bifrequency region to monitor depth of anesthesia was inferior to BIS technology.
Wavelet entropy is defined as the application of the Shannon function to each frequency scales in the wavelet domain; this technique has been implemented with some variations [12-14]. The importance of preprocessing the EEG signal was remarked; in order to reduce the amplitude effect in the brain waves, detrend of each epoch by its mean value and normalization by energy of the signal was applied [12]. This normalization minimizes the effect of signal amplitude on the frequency content, which leads to a better performance of the index. EOG and ECG are removed by wavelet techniques. Authors also suggest a method to choose the mother wavelet proposed by [15], the wavelet which maximizes the correlation coefficient between EEG signal, and the wavelet filter would be selected as the optimum mother wavelet. The study [14] combined wavelet transform, eigenvector and normalization techniques to develop a ZDoA Index which corresponds one of the five depths of anesthesia states to very deep anesthesia, deep anesthesia, moderate anesthesia, light anesthesia and awake. Simulation results based on real anesthetized EEGs demonstrate that the new index generally parallels the BIS index. In particular, the ZDoA index is often faster than the BIS index to react to the transition period between consciousness and unconsciousness for their data set in particular.
On the other hand, one of the advantages of the HHT is that it can break down a complicated EEG signal without a predefined basis function, such as sine or wavelet function, into several oscillatory functions that are embedded in the EEG signal, so it could provide a more precise time-frequency-scale representation. Combination of HHT and entropy analysis was done by [17]. They applied the Shannon entropy concept to the Hilbert-Huang spectrum, so a new entropy index could be obtained and was denoted as Hilbert-Huang Spectral entropy (HHSE). Consistent with the SE and RE in the M-Entropy Module (ME-SE/RE), authors proposed HHSE state entropy (HHSE-SE) computed over the frequency range
Conclusions
Nonlinear techniques such as entropy analysis in the time and frequency domains provide a high performance in EEG features extraction. ApEn and PE provide monotonically linearly separable features, so that the development of an index to classify between 'awake' and 'anesthetized' could use simple classifiers such as artificial neural networks, linear support vector machines, logistic regression or decision trees. The combination of entropy analysis, particularly the Shannon entropy concept with wavelet transform and Hilbert-Huang transform has shown promising results in the development of a new device for classifying depth of anesthesia states.
Because of the lack of a gold standard, it is still unclear the number of depth of anesthesia states that should be classified. Most groups develop a self clinical scale: [10] developed a scale of ten depth of anesthesia states; [14] divided the depth of anesthesia planes in five, from awake to unconsciousness; [8] only considered two different states 'awake' and 'anesthetized'. There are also some standard clinical scales, such as the Observer Alertness Sedation Scale; it could be a reference for the classification of depth of anesthesia [25].
References
1. American Society of Anesthesiologists. ''Practice Advisory for Intraoperative Awareness and Brain Function Monitoring''. Anesthesiology. Vol. 104. 2006. pp. 847-864. [ Links ]
2. J. Osterman, J. Hopper, W. Heran, T. Keane, B. Kolk. ''Awareness under anesthesia and the development of posttraumatic stress disorder''. General Hospital Psychiatry. Vol. 23. 2001. pp. 198-204. [ Links ]
3. P. Bischoff, I. Rundshagen. ''Awareness during general anesthesia''. Deutsches Ärzteblatt International. Vol. 108. 2011. pp. 1-7. [ Links ]
4. R. Nickalls, R. Mahajan. ''Editorial, Awareness and anaesthesia: think dose, think data''. British Journal of Anaesthesia. Vol. 104. 2010. pp. 1-2. [ Links ]
5. A. Anier, T. Lipping, V. Jäntti, P. Puumala, A. Huatori. Entropy of the EEG in transition to burst suppression in deep anesthesia: surrogate analysis. Proceedings of the 32nd Annual International Conference of the IEEE EMBS. Buenos Aires, Argentina. 2010. pp. 2790-2794. [ Links ]
6. N. Zhengqiang, L. Wang, J. Meng, F. Qiu, J. Huang. ''EEG signal processing in anesthesia: Feature extraction of time and frecuency parameters''. Procedia Environmental Sciences. Vol. 8. 2011. pp. 215-220. [ Links ]
7. W. Dong, C. Gui, Y. Ying, L. Lin, L. Guang, S. Wei. ''Application of nonlinear dynamics analysis in assesing unconsciousness: A preliminary study''. Clinical Neurophysiology. Vol. 122. 2011. pp. 490-498. [ Links ]
8. N. Nicolaou, P. Houris, P. Alexandrou, J. Georgiou. Entropy Measures for Discrimination of 'awake' Vs 'anaesthetized' State in Recovery from General Anesthesia. Proceedings of the 33rd Annual International Conference of the IEEE EMBS. Boston, USA. 2011. pp. 2598-2602. [ Links ]
9. L. Wang, N. Zhengqiang, J. Meng, F. Qiu, J. Huang. ''EEG under anesthesia: A general method for calculation of depth of anesthesia''. Procedia Environmental Sciences. Vol. 8. 2011. pp. 209-214. [ Links ]
10. P. Stacey, Z. Eugene, M. Zheng, M. Paul, B. Ian, B. David. ''Peak and averaged bicoherence for different EEG patterns during general anaesthesia''. Biomed Central - BioMedical Engineering. Vol. 9. 2010. pp. 76-97. [ Links ]
11. K. Hayashi, T. Sawa, M. Matsuura ''Anesthesia Depth-dependent Features of Electroencephalographic Bicoherence Spectrum during Sevoflurane Anesthesia''. Anesthesiology. Vol. 108. 2008. pp. 841-850. [ Links ]
12. Z. Toktam, B. Reza, D. Mahmood. ''A wavelet-based estimating depth of anesthesia''. Engineering Applications of Artificial Intelligence. Vol. 25. 2012. pp. 1710-1722. [ Links ]
13. T. Nguyen, P. Wen, Y. Li, R. Gray. ''Measuring and reflecting depth of anesthesia using wavelet and power spectral density''. IEEE Transaction on information technology in biomedicine. Vol. 15. 2011. pp. 630-639. [ Links ]
14. T. Nguyen, P. Wen, Y. Li, M. Malan. ''Measuring the hypnotic depth of anaesthesia based on the EEG signal using combined wavelet transform, eigenvector and normalisation techniques''. Computers in biology and medicine. Vol. 42. 2012. 680-691. [ Links ]
15. B. Singh, A. Tiwari. ''Optimal selection of wavelet basis function applied to ECG signal denoising''. Digital Signal Processing. Vol. 16. 2006. 275-287. [ Links ]
16. N. Huang, Z. Wu, S. Long. ''Hilbert Huang Transform''. Scholarpedia. Vol. 3. 2008. pp. 2544. [ Links ]
17. X. Li, D. Li, Z. Liang, L. Voss, J. Sleigh. ''Analysis of depth of anesthesia with Hilbert–Huang spectral entropy''. Clinical Neurophysiology. Vol. 119. 2008. pp. 2465-2475. [ Links ]
18. P. Steven, H. Wei. ''Approximate entropy: Statistical properties and applications''. Communications in Statistics - Theory and Methods. Vol. 21. 1992. pp. 3061-3077. [ Links ]
19. H. Viertiö, V. Maja, M. Särkelä, P. Talja, N. Tenkanen, H. Laakso. ''Description of the EntropyTM algorithm as applied in the Datex-Ohmeda S/5TM Entropy Module''. Acta Anaesthesiologica Scandinavica. Vol. 48. 2004. pp. 154-161. [ Links ]
20. B. Christopher, P. Bernd. ''Permutation entropy - a natural complexity measure for time series''. Procedia Environmental Sciences. Vol. 88. 2002. pp. 4102-4106. [ Links ]
21. E. Olofsen, J. Sleigh, A. Dahan. ''Permutation entropy of the electroencephalogram: a measure of anaesthetic drug effect''. British Journal of Anaesthesia. Vol. 101. 2013. pp. 810-821. [ Links ]
22. S. Mallat. ''A theory for multiresolution signal decomposition: the wavelet representation. Pattern analysis and Machine Inteligence''. IEEE transaction on. Vol. 11. 1989. pp. 674-693. [ Links ]
23. I. Rampil. ''A primer for EEG signal processing in anesthesia''. Anesthesiology. Vol. 89. 1998. pp. 980-1002. [ Links ]
24. R. Rodrigues, I. Miranda, J. García, S. Benevides, Y. Barbosa, D. Abitbol. ''Bispectral index and other processed parameters of electroencephalogram: an Update''. Revista Brasileira de Anestesiologia. Vol. 62. 2012. pp. 105-117. [ Links ]
25. C. Chisholm, J. Zurica, D. Mironov, E. Ornstein, E. Heyer. ''Comparison of Electrophysiologic Monitors with Clinical Assessment of Level of Sedation''. Mayo Clinic Proceedings. Vol. 81. 2006. 46-52. [ Links ]