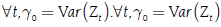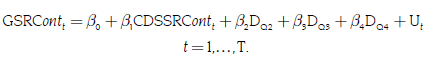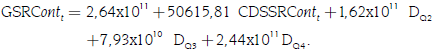INTRODUCCIÓN

La dinámica del gasto en salud de las empresas prestadoras de los servicios de salud (EPS) en Colombia desde el año 2004 se ha visto influenciada por diferentes factores para los regímenes contributivo y subsidiado¹. El primer régimen se ha visto afectado por el importante crecimiento de los pagos a través del Fosyga² por concepto de recobros a las EPS por medicamentos no plan obligatorio de salud (POS)³ y por el crecimiento de los afiliados (MinSalud, 2014).

Por su parte, el segundo régimen ha estado dinamizado por las decisiones de Gobierno de aumentar progresivamente la cobertura de afiliación a este régimen, así como por la igualación de los planes de beneficios en pro de lo dispuesto por la Sentencia T-760 de 2008⁴ de la Corte Constitucional. Para el primer lustro de la segunda década del siglo XXI, el gasto total en salud representó aproximadamente el 7% del producto interno bruto colombiano, 0,8% más que lo registrado en el período 2001-2010 (^{MinSalud, 2014)}.

Este artículo tiene por objetivo determinar si existe un comportamiento estacional en el gasto en salud de las entidades prestadoras de los servicios de salud de los regímenes contributivo y subsidiado en el país. El análisis exploratorio de la estacionalidad ayuda a los hacedores de política a obtener información primordial sobre la identificación de patrones en el sector salud y/o pautas repetitivas en el comportamiento dinámico de algunos tipos especiales de cuentas financieras.

Así, en este trabajo se adopta la definición de estacionalidad de ^{Box y Jenkins (1976)}, la cual indica que el efecto estacional implica que una observación de un trimestre en particular, por ejemplo el segundo trimestre (T2), está relacionada con las observaciones de los segundos trimestres previos.

El artículo está estructurado de la siguiente forma: en la primera sección se realiza una revisión de literatura. El segundo aparte expone la construcción de los datos, partiendo de los planes de cuentas de las EPS públicas y privadas. Las metodologías para determinar la existencia o no de estacionalidad y sus respectivos resultados estadísticos se presentan, respectivamente, en la tercera y cuarta secciones. En la última sección se concluye.

1. REVISIÓN DE LITERATURA

La estacionalidad del gasto en salud no ha sido muy estudiada en la literatura internacional; no obstante, los determinantes del gasto en salud sí han sido objetivo de múltiples investigaciones en diferentes países.

Este es el caso de los trabajos de ^{Gerdtham et al. (1992)}, ^{Hitiris y Posnett (1992)}, ^{Hansen y King (1996)}, ^{Albouy, Davezies y Debrand (2010)} y ^{Murthy y Okunade (2016)}, quienes principalmente se concentran en la relación ingreso-salud para algunos países de la Organización para la Cooperación y el Desarrollo Económico (OCDE), mientras que las investigaciones de ^{Govindaraj, Chellaraj y Murray (1997)}, Samudram, Nair y Vaithilingam (2009), ^{Tang (2009)}, ^{Clements, Faircloth y Verhoeven (2007)} y ^{Ke, Saksena y Holly (2011)} revisan el tema para países en desarrollo.

En términos generales, los estudios encuentran que, además de ser el ingreso un factor determinante en la demanda de servicios de salud, los factores institucionales y socio-demográficos (p. e. el nivel educativo, la situación económica de los padres y el poseer un empleo) juegan un papel fundamental. También se señala que el gasto gubernamental en salud y los gastos de bolsillo⁵ siguen distintos caminos, y que el ritmo de crecimiento del gasto en salud es diferente para cada país, en función de su nivel de desarrollo económico.

Ya en relación concreta con la estacionalidad del gasto en salud, aunque no existen estudios que revisen su comportamiento. ^{Ferrand et al. (2011)} estudian la evolución temporal del gasto de los programas de Medicaid en agentes antidepresivos en EE. UU. Para ello, estiman modelos autorregresivos integrados de media móvil (ARIMA) con intervenciones (en especial las relacionadas con la entrada de medicamentos de marca y genéricos y la publicidad directa al consumidor). Los autores encuentran que la entrada de medicamentos genéricos no condujo a una reducción de los gastos generales, siendo estos últimos no estacionales.

Bajo otro tópico de estudio, ^{Loh (2015)} busca comprender mejor las tendencias y determinantes de las actividades de turismo de salud en Canadá entre los años 1970 y 2010. Para ello, sigue una metodología de regresiones auxiliares sobre los residuales (con la que se contrasta la existencia de quiebres estructurales) y modelos autorregresivos de media móvil con variables exógenas (ARMAX). Se encuentra que el turismo de salud aumenta cuando la inversión privada en instalaciones médicas disminuye, siendo una de las posibles causas de este cambio estructural el Acuerdo General sobre el Comercio de Servicios (AGCS), que entró en vigor en 1995.

El trabajo de ^{Safaeian et al. (2015)} tiene por finalidad evaluar el patrón de estacionalidad y los factores relacionados con la prescripción de antibióticos en Isfahan (Irán). A través de una encuesta transversal se aplican múltiples modelos de regresión logística. Esta investigación concluye la existencia de un pico estacional en otoño de las recetas de penicilinas y cefalosporinas.

Uno de los estudios más recientes es el de ^{Albert et al. (2015)}, donde se quiere conocer si las estaciones climáticas afectan los gastos de atención médica (MCE) en las personas de avanzada edad en Holanda. Para la descomposición estacional y de tendencia los autores aplican el método de Loess, usando la prueba t de Welch. Se concluye que las estaciones climáticas sí afectan los gastos, dado que aumentan las tasas de mortalidad y de hospitalización.

Para Colombia, uno de los primeros análisis formales sobre el gasto en salud fue el de ^{O’Meara, Ruiz y Amaya (2003)}; no obstante, contempla un análisis netamente descriptivo y no se tratan temas de estacionalidad en específico.

Por ende, el objetivo de este artículo se considera novedoso para la literatura colombiana.

2. DATOS A MODELAR

En este documento el gasto en salud se entiende como el monto asignado por las EPS (indiferente del régimen perteneciente) a los productos y a los servicios prestados durante el ejercicio de sus labores. Bajo tal concepto, para las estimaciones del gasto en salud en las empresas de carácter privado, teniendo como marco de referencia el Plan Único de Cuentas (PUC) dispuesto en la Resolución 4175 de 2014 de la Superintendencia Nacional de Salud, se tomaron las cuentas relacionadas en la tabla 1 ⁶.

Tabla 1 Cuentas seleccionadas del PUC de la Resolución 4175 de 2014 de la Superintendencia Nacional de Salud (para empresas privadas) 

Fuente: elaboración propia

Por otra parte, para las empresas de carácter público se consideraron, del PUC estipulado en la Resolución 414 de 2014 de la Contaduría General de la Nación, los rubros presentados en la tabla 2 ⁷.

Tabla 2 Cuentas seleccionadas del PUC de la Resolución 414 de 2014 de la Contaduría General de la Nación (para empresas públicas) 

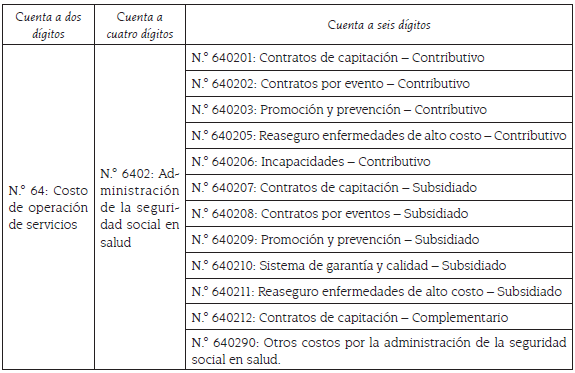
Fuente: elaboración propia

Para el régimen contributivo, se consideró la totalidad de las EPS (14) del Sistema General de Seguridad Social en Salud (SGSSS). En el régimen subsidiado se tomaron 25 entidades (las cuales representan más del 80% de los gastos totales en salud de este régimen), entre ellas, cajas de compensación familiar, empresas solidarias de salud y empresas promotoras de salud autorizadas para administrar recursos del régimen subsidiado⁸ (se excluyen las EPS indígenas dado que sus sistemas de información no presentan una buena calidad). La periodicidad es trimestral, desde el primer trimestre (T1) del año 2011 hasta el cuarto trimestre (T4) del año 2015⁹. Estos valores monetarios fueron deflactados por el IPC salud con año base 2011 (información obtenida del Departamento Administrativo Nacional de Estadística -DANE-).

3. METODOLOGÍAS ESTADÍSTICAS PARA DETERMINAR ESTACIONALIDAD

Esta sección muestra las diferentes técnicas estadísticas aplicadas para el estudio del efecto de estacionalidad, como lo son el método gráfico, las tasas de crecimiento trimestre a trimestre, los correlogramas simples y parciales, la prueba no paramétrica de Kendall, el análisis de regresión con inclusión de variables dummies estacionales y los procesos estocásticos SARIMA (p,d,q)(P,S,Q) _s .

3.2. Correlogramas simples (FAC) y parciales (FACP)

Sea {Z _t } un proceso estacionario con E(Zt) = μ y Var(Z _t ) = σ² constantes, se define la función de autocovarianza (FACV) como:

(1)

La autocorrelación (ρ _k ) mide la relación (o dependencia, más no causalidad) entre dos variables separadas por k períodos. De esta manera, la función de autocorrelación simple (FAC) se expresa mediante la ecuación [2].

(2)

Luego, todo proceso estacionario satisface las siguientes cinco características (^{Tsay, 2005}) ¹⁰:

i)

ii)

iii) se tiene que

iv) 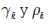son simétricas con respecto a k, es decir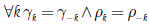

v) 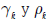son semidefinidas positivas. Es decir, se satisfacen las siguientes desigualdades:

Por otra parte, la autocorrelación parcial mide la dependencia entre Zt y Z t−k cuando se elimina el efecto de Z t-1, Z t-2,…,Z t-k+1.Se expresa mediante:

(3)

Ahora, los correlogramas simples y parciales hacen referencia a una representación gráfica de las autocorrelaciones simples y parciales de la muestra, respectivamente, versus el tiempo. Si cada cierto número de período aumentan significativamente las autocorrelaciones, ello daría muestras de posibles estacionalidades.

3.3. Prueba no paramétrica de Kendall

Este contraste de estacionalidad basado en rangos, desarrollado por ^{Kendall y Ordb (1990)}, consiste en ordenar las observaciones de cada trimestre y asignarles un valor de 1 a la menor, hasta 4 a la mayor. A continuación, para cada trimestre se suman los valores de todos los años, por lo que:

(4)

Donde ( representa el número de años de la muestra. Así, bajo la hipótesis nula de no existencia de estacionalidad, el estadístico a calcular sigue la expresión:

(5)

Donde r es el número de observaciones por año (4 con datos trimestrales). Tal estadístico se distribuye como una X2 con (r - 1) grados de libertad. Luego, para valores grandes de K (superiores al cuantil considerado de la X2) se concluye que existe componente estacional.

3.4. Análisis de regresión con inclusión de variables dummies estacionales

En la regresión lineal múltiple de Y sobre X1,…, XK se admite que la función de regresión tiene la expresión (6).

(6)

Al contemplar una muestra de T datos en los que se observa las variables Y y X = (X1,.…, XK)' se tiene (xt,yt), i = 1,…,t, donde xt = (xt1, xt2, …, xtK). Luego, el modelo de regresión lineal múltiple asume que:

(7)

Donde las perturbaciones Ut verifican las siguientes hipótesis:

i) E(Ut)=0, para cada t=1,…, T

ii) Var (Ut)=σ2, para cada t=1,…, T

iii) E (Ut Ui)=0,

iv) Ut~ Normal (0,σ2 ),

v)

vi) Las variables Xt son linealmente independientes entre sí (no hay colinealidad).

Así, para este estudio se plantean las ecuaciones (8) y (9).

(8)

(9)

Donde GSRcontt es el gasto en salud en el régimen contributivo en el período t; GSRSubst es el gasto en salud en el régimen subsidiado en el período t; CDSSRContt es la cantidad demandada de servicios de salud en el régimen contributivo en el período t; CDSSRSubst es la cantidad demandada de servicios de salud en el régimen subsidiado en el períodot, y DQi es una variable dummy que toma el valor de 1 cuando se está en el período trimestral i, con i = 2,3,4¹¹.

Las variables CDSSRContt y CDSSRSubst hacen referencia al número de servicios de demanda por hospitalización, medicamentos, nacidos, procedimientos y urgencias por cada régimen. Estos valores son tomados de la base de datos de Registros Individuales de Prestación de Servicios de Salud (RIPS), establecida por la Resolución 3374 de 2000 del Ministerio de Salud¹².

Dada la estructura de la ecuación (7), en este sistema estadístico la estacionalidad se determina si al menos uno de los parámetros es estadísticamente significativo. Y el parámetro se puede interpretar como una variable control.

3.5. Procesos estocásticos SARIMA (p,d,q)(P,D,Q) _s .

Es considerado uno de los mejores modelos lineales para ajuste de series económicas, por su estructura dinámica constituida en la búsqueda de patrones históricos, con la premisa de que las futuras estimaciones solo dependen del pasado de la serie (de su inercia) y no de variables independientes (^{Brockwell y Davis, 2002}). En la literatura este tipo de proceso estocástico se considera por excelencia uno de los mejores métodos para representar los componentes estacionales.

Adentrándose al aspecto formal, este modelo captura la característica estacional y cíclica de la serie de interés, entendiendo por cíclica la asociada al componente autorregresivo y de media móvil. Se expresa como sigue en (10).

(10)

Donde Φ(L) es el polinomio de coeficientes, con operador de rezagos L del componente autorregresivoAR; y Φs(L) el símil al caso anterior, pero aplicado al proceso autorregresivo de la parte estacional SAR. Además, Φ(L) y Φs(L) son los polinomios de coeficientes del componente de media móvil MA y su análogo estacional SMA, respectivamente.

El término Ruido Blanco es el término de las innovaciones, d es el orden de integración del proceso no estacional (número de raíces unitarias no estacionales) y D es el orden de integración del proceso estacional (número de raíces unitarias estacionales) (^{Greene, 2008}).

Para su aplicación se utiliza por lo general la metodología de ^{Box y Jenkins (1976)} referente a las etapas de identificación, estimación, contraste y predicción.

4. RESULTADOS CUANTITATIVOS

4.1. Método gráfico y tasas de crecimiento trimestre a trimestre¹³

Los datos presentados en la gráfico 1 no dan señales de que en el régimen contributivo haya presencia de estacionalidad, caso contrario al gráfico 2, donde se observan picos en el cuarto trimestre de los diferentes años de análisis.

Fuente: elaboración propia

Gráfico 1 (a) Gasto de salud en el régimen contributivo (en millones de pesos colombianos reales, 2011T1=100) y (b) su tasa de crecimiento 

Fuente: elaboración propia

Gráfico 2 (a) Gasto de salud en el régimen subsidiado (en millones de pesos colombianos reales, 2011T1=100) y (b) su tasa de crecimiento 

Similar comportamiento se obtiene al observar las tasas de crecimiento trimestral (tabla 1). En el régimen contributivo no hay un patrón definido, mientras que en el régimen subsidiado las tasas más altas se evidencian en el cuarto trimestre (columna T4), donde siempre se tienen crecimientos mayores al 10%, atípicos para el resto de trimestres (T1, T2 y T3).

Tabla 1 Tasas de crecimiento trimestral del gasto de salud (porcentajes). 

Fuente: elaboración propia

4.2. Correlogramas simples y parciales

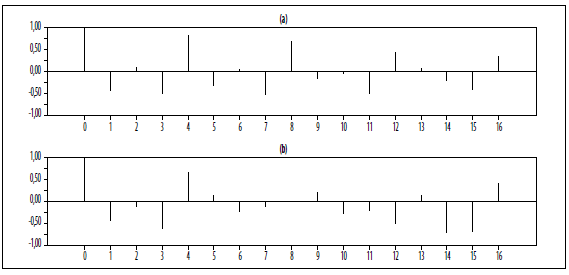
La función de autocorrelación simple (FAC) y parcial (FACP) de la variable dif _ ln(GSRCcont)t no presenta signos de estacionalidad (gráfico 3); no obstante, la FAC de la variable dif _ ln(GSRSubs) _t sí muestra correlaciones más altas que el promedio en los períodos 4 y 8 (gráfico 4).

Fuente: elaboración propia

Gráfico 3 (a) FAC y (b) FACP de la variable dif_ln(GSRCcont)t hasta el rezago 16 

Fuente: elaboración propia

Gráfico 4 (a) FAC y (b) FACP de la variable dif_ln(GSRSubs)t hasta el rezago 16 

4.3. Prueba de Kendall

El contraste no paramétrico de Kendall arroja que para ambos casos (regímenes contributivo y subsidiado) no se rechaza la hipótesis nula de no estacionalidad, a un nivel de significancia del 5%. Es decir que calculados los estadísticos, se establece que no hay evidencias estadísticas de componentes estacionales (tabla 2).

Tabla 2 Resultados contraste de Kendall 

Fuente: elaboración propia

4.4. Análisis de regresión múltiple y dummies estacionales

Los resultados de la estimación de [8] se presentan en la tabla 3, por lo que se tiene la siguiente ecuación:

Los coeficientes β0 y β1 son estadísticamente diferentes de cero a un alfa del 5%. Aunque el coeficiente del cuarto trimestre (β4) no es significativo, es el de más alto valor.

Tabla 3 Coeficientes del modelo de regresión múltiple para el régimen contributivo¹⁴  

Variable	Coeficiente	Error estándar	Estadístico t	P-valor
β0	2,64x1011	5,25x1010	5,026	0,000
β1	50615,81	6406,316	7,901	0,000
β2	1,62x1011	3,51x1011	0,461	0,653
β3	7,93x1010	2,94x1011	0,270	0,792
β4	2,44x1011	2,87x1011	0,850	0,411

Fuente: elaboración propia

Los resultados de la estimación de [9] se presentan en la tabla 4. De manera que:

Referente a la estimación de los parámetros de la ecuación [9] (tabla 4), se puede observar que el coeficiente ∝1 es el único estadísticamente diferente de cero a un alfa del 5%; no obstante, aunque el coeficiente del cuarto trimestre (∝4) no es significativo, sí es cierto que es el de más alto valor, por encima de los parámetros del segundo (∝2) y tercer (∝3) trimestres.

Tabla 4 Coeficientes del modelo de regresión múltiple para el régimen subsidiado  

Variable	Coeficiente	Error estándar	Estadístico t	P-valor
∝0	2,74x1011	3,13x1011	0,876	0,397
∝1	59593,40	8906,228	6,691	0,000
∝2	-1,53x1011	2,63x1011	-0,582	0,571
∝3	-4.60x1011	2,62x1011	-1,752	0,103
∝4	9,97x1010	3,59x1011	0,278	0,785

Fuente: elaboración propia

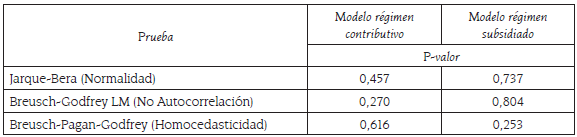
En la tabla 5 se presentan todas las pruebas sobre los residuales de los modelos de regresión estimados, donde se observa un buen comportamiento, al no rechazar las hipótesis nulas de normalidad, no autocorrelación y homocedasticidad, en un nivel de significancia del 5%.

Tabla 5 Validación de los residuales de los modelos de regresión múltiple 

Fuente: elaboración propia

4.5. Procesos estocásticos SARIMA (p,d,q)(P,D,Q)s

Antes de realizar el ajuste y la estimación de los modelos mediante máxima verosimilitud, se aplicaron las pruebas de raíces unitarias Dickey-Fuller Aumentada (ADF), Phillip-Perron (PP) y Kwiatkowski-Phillips-Schmidt-Shin (KPSS) a las variables ln(GSRCont)t y dif _ ln(GSRSubs)t , para determinar si son estacionarias o no. La tabla 6 muestra que en un nivel de significancia del 5%, para las pruebas ADF y PP se rechaza la hipótesis nula de raíz unitaria, y para la KPSS no se rechaza la hipótesis nula de estacionariedad.

Tabla 6 Pruebas de raíz unitaria ADF, PP y KPSS 

Fuente: elaboración propia

Para el caso del régimen contributivo, basándose en los criterios de información Akaike y BIC, y en el buen comportamiento de los residuales, se logró ajustar un modelo Arima (7,1,3) para la serie ln(GSRCont)t, estimando solo los coeficientes φ1, φ4, φ7 y θ3 (tabla 7). Todos los coeficientes son significativos a un alfa del 5%, menos φ7, el cual se hace necesario incluir para tener unos residuales no correlacionados. No hubo necesidad de contar con parte estacional para la modelación.

Tabla 7 Estimación de coeficientes del proceso ARIMA(7,1,3) para ln(GSRCont)t 

Variable	Coeficiente	Error estándar	Estadístico t	P-valor
φ1	0,481	0,114	4,199	0,003
φ4	0,501	0,177	2,824	0,022
φ7	0,155	0,103	1,509	0,170
θ3	-1,014	0,250	-4,053	0,004

Fuente: elaboración propia

La tabla 8 evidencia el comportamiento de ruido blanco de los residuales del modelo ARIMA (7,1,3) para la serie ln(GSRCont)t, no rechazando las hipótesis nulas de normalidad y de no autocorrelación. Al calcular la prueba no paramétrica CUSUM que tiene por hipótesis nula la buena especificación del modelo, en un nivel de confianza del 95%, se observa que estos presentan un comportamiento adecuado (gráfico 5).

Tabla 8 Validación de los residuales del proceso ARIMA (7,1,3) para ln(GSRCont)t, 

Prueba	P-valor
Jarque-Bera (Normalidad)	0,488
Ljung-Box (No Autocorrelación)	0,010

Fuente: elaboración propia

Fuente: elaboración propia

Gráfico 5 Prueba no paramétrica de especificación CUSUM sobre los residuales del proceso ARIMA (7,1,3) para ln(GSRCont)t, 

Por otra parte, para el caso del régimen subsidiado, basándose en los criterios de información Akaike y BIC, y en el buen comportamiento de los residuales, se logró ajustar un modelo SARIMA (0,1,2)(1,0,0)s para la serie ln(GSRSubs)t (tabla 9). Todos los coeficientes son significativos a cualquier nivel de significancia común.

Para estos datos, fue necesario incluir el componente estacional en el modelo de series temporales¹⁵.

Tabla 9 Estimación de coeficientes del proceso SARIMA (0,1,2)(1,0,0)s para ln(GSRSubs)t 

Variable	Coeficiente	Error estándar	Estadístico t	P-valor
θ1	1,182	0,486	2,432	0,032
θ2	-1,888	0,723	-2,612	0,023
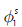
	0,874	0,064	13,580	0,000

Fuente: elaboración propia

De otro lado, la tabla 10 y el gráfico 6 muestran un correcto comportamiento en los residuales para la serie correspondiente al gasto del régimen subsidiado.

Tabla 10 Validación de los residuales del proceso SARIMA (0,1,2)(1,0,0)s para ln(GSRSubs)t 

Prueba	P-valor
Jarque-Bera (Normalidad)	0,111
Ljung-Box (No Autocorrelación)	0,120

Fuente: elaboración propia

Fuente: elaboración propia

Gráfico 6 Prueba no paramétrica de especificación CUSUM sobre residuales del proceso SARIMA (0,1,2)(1,0,0)s para ln(GSRSubs)t 

5. CONCLUSIONES

En este estudio evalúa si el gasto en salud de los regímenes contributivo y subsidiado se comporta estacionalmente. Para ello se revisan cinco diferentes procedimientos cuantitativos. Para el régimen contributivo no se halla evidencia de estacionalidad. No obstante, se encuentra que en el régimen subsidiado sí se presenta evidencia estadística de tal componente (así lo expresan tres de los cinco métodos desarrollados), específicamente en su cuarto trimestre, período temporal en el que se observa un crecimiento mayor al de los otros trimestres (tabla 11).

Tabla 11 Resumen de evidencias sobre estacionalidad 

Fuente: elaboración propia

Al obtener estos resultados, se procedió a indagar al detalle cuáles eran las cuentas financieras con mayor variación en su cuarto trimestre (T4), y se encontró que son las relacionadas con Contratos por evento (N.° 616540) y Contratos por eventos - Subsidiado (N.° 640208), rubros que evidencian los pagos que se realizan por las actividades, procedimientos, intervenciones, insumos y medicamentos prestados o suministrados a un paciente ligado a un evento de atención en salud.

Este hecho parece tener su fundamento, entre otras razones, en el aumento de los servicios demandados en los meses finales del año¹⁶, dado que al aumentar el número de estas unidades de pago (constituidas por cada actividad, procedimiento, intervención, insumo o medicamento prestado o suministrado, con unas tarifas pactadas previamente), el gasto tiende a incrementar significativamente.

Otro aumento importante, aunque solo referente al último año de análisis (2015), es el relacionado con la cuenta Seguridad social en salud (N.° 616565). Ello, debido a la implementación por parte de las EPS subsidiadas de lo dispuesto en el Decreto 2702 de 2014 del Ministerio de Salud y Protección Social, donde se establecen las directrices para la constitución de sus reservas técnicas.

De esta manera, el presente artículo de investigación muestra la importancia de entender la estacionalidad estadística a partir de los cambios regulares a través del tiempo, aportando así, conocimientos a la predicción de tendencias (patrones de conducta) respecto al flujo monetario, desde una visión macroeconómica del gasto en salud para Colombia. En unos años, con series de longitud más extensas, nuevos trabajos podrán construir modelos de pronósticos que incorporen el concepto de estacionalidad dentro de sus características intrínsecas.

Para próximas investigaciones, se deberá estudiar la dinámica del gasto en salud de las entidades promotoras de salud indígenas (que no fueron tenidas en cuenta para este documento), las cuales en la actualidad no cuentan con sistemas de información de calidad y la información que presentan en sus reportes evidencian esta debilidad. Adicionalmente, en el corto plazo será beneficioso analizar cuantitativamente el comportamiento de todos los gastos referentes al concepto de reservas, tema aún no consolidado por completo en la estructura financiera de las EPS (especialmente en las del régimen subsidiado).