Ernesto Cárdenas¹

1 Researcher, Department of Economics, Universidad Externado de Colombia, Bogotá Colombia. (email: ernesto.cardenas@uexternado.edu.co). The author gratefully acknowledges the helpful comments of two anonymous referees.

Abstract

Theoretically, polarization is associated with a higher probability of social conflict. This paper, in a microeconomic model based on the theory of social networks, analyses how changes in the network's structure affect the level of some basic parameters associated with the concept of polarization. This study shows that under upward monotonic preferences, longer sets of affiliations for each individual reduce polarization, whereas under downward monotonic preferences, longer sets of the so-called bad affiliations increase polarization. Finally, in the case of a non-monotonic system of preferences, an expansion of the affiliations set will alter the resulting polarization order in different ways depending on the preferences themselves.

Keywords: Polarization, conflict, preferences, theory of networks.

JEL: D71, D74.

Resumen

En la teoría, la polarización se asocia con una mayor probabilidad de conflicto social. Este artículo analiza, dentro de un modelo microeconómico basado en la teoría de redes sociales, cómo los cambios en la estructura de la red afectan el nivel de algunos parámetros básicos asociados con el concepto de polarización. También muestra que bajo preferencias monótonas crecientes, la existencia de conjuntos más largos de afiliaciones para cada individuo reduce la polarización, mientras que, bajo preferencias monótonas decrecientes, los conjuntos más largos de las llamadas malas afiliaciones aumentan la polarización. Por último, en el caso de un sistema no monótono de preferencias, una expansión del conjunto de afiliaciones alterará el orden resultante de polarización de diferentes maneras, dependiendo de las preferencias mismas.

Palabras clave: polarización, conflicto, preferencias, teoría de redes.

JEL: D71, D74.

Résumé

Mots-clés : polarisation, conflit, préférences, théorie de réseaux.

JEL : D71, D74.

Este artículo fue recibido el 6 de junio de 2013, ajustado el 9 de diciembre de 2013 y su publicación aprobada el 12 de diciembre de 2013.

INTRODUCTION

The opening words of Amartya Sen's famous book on economic inequality are "The relation between inequality and rebellion is indeed a close one, and it runs both ways" (Sen & Foster, 1997). However, recent literature in economics has raised questions about the accuracy of the very concept of inequality and its correlation with social conflict (Esteban & Ray, 1994, 1999). As a result, it seems that the concept of polarization is better suited than that of inequality for explaining the probability of social conflict.

Not surprisingly, in his recent work on Identity and Violence, Sen himself rests on the notions underlying the concept of polarization, those of within-group homogeneity and between-group heterogeneity:

"A sense of identity can be a source not merely of pride and joy but also of strength and confidence... And yet identity can also kill-and kill with abandon. A strong-and exclusive-sense of belonging to one group can in many cases carry with it the perception of distance and divergence from other groups. Within-group solidarity can help to feed between-group discord" (Sen, 2006, pp. 1-2).

Reductionist ideologies based on defining individuals or societies in terms of a unique affiliation can be used to foster strong feelings of within-group solidarity, but also ones of between-group disagreement. Thus, it becomes easier to promote conflict as a social outcome. The problem with these theories is that they reduce a multidimensional issue to an unidimensional one.

As an example, consider Huntington's theory of the clash of civilizations (Huntington, 1996) in which religion is the only affiliation considered when talking about civilizations and conflict. Following Sen's analysis of this theory, the classification of people in terms of belonging either to Western civilization or Islamic civilization is based on two misconceptions. First, the very idea of classifying people into either one of the two civilizations is an extreme reductionist view that misses the complexity of the essence of human beings; and second, to assume that individuals in each of these civilizations must have a sense of antagonism towards those who belong to the other group ignores the multiple affiliations of individuals. In fact, every individual belongs to different social groups and, therefore, has multiple affiliations, each of which confers a specific identity to that individual: profession, employment, family role, preferences for music, sports or politics are just a few examples.

Similar examples of reductionism, with social conflict as an outcome, can be found all over the world. In Rwanda, perception of individuals only in terms of ethnicity as either Hutu or Tutsi kept the country in continuous civil war and produced atrocities such as the 1995 genocide, which caused almost one million causalities in just a few days. According to Sen, Bangladesh obtained its independence from Pakistan in 1971 after a bloody civil war due to the reduction of individuals' affiliations to just one, that of language. In Colombia, where peace has become extremely difficult to achieve, both sides in the conflict have a reductionist view. The Fuerzas Armadas Revolucionarias de Colombia (FARC) perceive society as being the status quo they want to change, whereas most of that same society only perceive the FARC as mere terrorists. In Syria, since the outset of the war in 2011, things have been difficult for the rebeals because of the lack of weapons, combatants and a unified ideology among the different small rebel groups. However, the reductionist view of the conflict-for or against Assad-has intensified the conflict enormously. Following conservative numbers, there are more than 65.000 thousand deaths due to the armed conflict.

Recognition of the fact that individuals have multiple affiliations expands the spectrum of commonalities among people and abates their sense of antagonism.

Societies where the multiple affiliations of individuals are taken into account generate more peaceful environments as social outcomes. Switzerland, for example, where Germans, French and Italians are the three main groups forming the society and where each of their languages is classed as one of the country's official languages is a good example of a peaceful environment with individuals having different affiliations.

In economics, most of the work relating to polarization and conflict has been undertaken considering unidimensional categories for defining groups within society. Examples of polarization analysis, in terms of only one relevant characteristic, are those by Gasparini, Horenstein, Molina and Oliveri (2008), based on income; Montalvoa and Reynal-Querol (2003) and Reynal-Querol (2002b), based on religion; or Reynal-Querol (2002a), based on ethnicity.

The main contribution of this work is to use social networks theory as a way to deal with the fact that individuals have multiple affiliations. Specifically, with a microeconomic model based on the theory of social networks, this study analyzes how changes in the structure of a given network, representing a given society, affect the level of some basic parameters of the network which, in turn, are associated with the concept of polarization and, as a consequence, its relation with social conflict.

Here, it is assumed that each individual has not just one, but several affiliations. Affiliations of individuals and their relationships are captured by means of a hypergraph. Each individual is endowed with a preference system over the set of all possible affiliations (i.e. the power set of the set of affiliations) so that she can choose among all of them. Both, the hypergraph and the preference system induce a communication graph.

Two specific preference systems are analyzed: a monotonic and a non-monotonic system. Under the monotonic system, two individuals decide to communicate with each other if they mutually consider the other's set of affiliations as being at least as good as its threshold affiliations system set i.e. the set of minimum affiliations she considers crucial for communicating with someone else.

The non-monotonic system is obtained by positing thresholds of good combinations of affiliations and ceilings of bad combinations of affiliations. In other words, each individual has an exhaustive partition over the set of all possible affiliations. Here, two individuals communicate if the affiliations of each individual are considered as good as their own good affiliations and none of them are considered bad affiliations.

If communication among individuals occurs, then, they will be linked in the associated communication graph.

The paper proceeds as follows. Some basic concepts derived from the theory of networks are introduced in section 2. Section 3 outlines the concept of polarization and formally defines two (pre)orders for ranking networks in terms of polarization. A model of social communication based on characteristics of the social structure, represented here by means of an hypergraph, and a system of social preferences is developed in section 4. Section 5 presents some comparative statics excercises; in particular, the analysis of how changes in the affiliation sets for each individual and changes in social preferences, may alter the degree of social polarization through changes in the associated communication network. Finally, the conclusions of the work are presented.

This section presents a definition of the concepts of the theory of networks and groups that will be used throughout to be related with the notion of polarization and for building up the microeconomic model in order to perform comparative statics².

Definition 1 (Hypergraph) A hypergraph H=(V,E) consists of a set of vertices or nodes and a set of hyperedges which is nothing more than a collection of subsets of V. Each hyperedge, therefore, contains one or more vertices and we say that those vertices are linked by that particular hyperedge.

Definition 2 (Network) A network 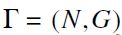consists of a set of nodes and a set of links Each link g_i is identified by the pair of respective nodes which are connected by g_i. Each link in G represents a relationship between nodes i and j.

Definition 5 (Component) A (connected) component of a network Γ=(N,G), is a nonempty subnetwork C'=(N',G'), such that

if and , then there exists a path in G' between i and j, and

if i then there does not exists a path in G between i and j.

Thus, the components of a network are the distinct maximal connected subgraphs of a network. The set of components of Γ is denoted C(Γ). Note that .

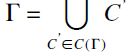Definition 6 (Clique) A clique is a maximal completely connected subnetwork Q of a given network Γ.

It is noteworthy to note that a clique is a maximal completely connected subnetwork while a component is a maximal path-connected subnetwork. Neither implies the other.

Definition 7 (Relative Size) Given a network Γ with more than one component, the relative size of a component by

Definition 8 (Overall Clustering Coeficient) It is a measure of the average probability that two nodes k,j directly connected to node i are also connected among themselves

Definition 9 (Star) A hypergraph H=(V,E) is called a star if there is a node which belongs to all hyperedges.

Definition 10 (Representative Graph of a Hypergraph) Let be a hypergraph with n edges. The representative graph of H is defined to be the simple graph of order n whose nodes 1, 2,..., n respectively represent the edges e₁, e₂,..., e_n of Hand with nodes 1 and j joined by an edge if, and only if, .

This section presents the definition of polarization and that of two (pre)orders for ranking different networks in terms of polarization. The first is a (pre)order based on the relative size of the main components of a network and, the second, is based on the clustering coefficient. The two (pre)orders will be referred to as component-size polarization and clustering polarization respectively.

Polarization

In general, and following (Esteban and Ray, 1994), three basic elements must be present when talking about social polarization and to consider it as a threat for social order:

1) There must be a small number of significantly sized groups,

2) An individual belonging to any of the groups must feel a sense of identification or within-group homogeneity with the rest of individuals belonging to the same group and,

3) Individuals belonging to the same group must feel some degree of distance or between-group heterogeneity from individuals belonging to other groups.

The idea of component-size polarization captures the need for small, but significantly sized different groups within society as a pre-requirement for polarization. Thus, we base this component-size polarization preorder in the network-theoretic notion of components (definition 5 in the previous section).

The following axioms define the component-size polarization:

Axiom 1 Consider any two networks with the same population i.e. N¹=N² and let be the set of ordered components, in terms of size, from higher to lower, of network i. Then, other things being equal, whenever . i.e. the cardinality for one of the two largest components in Γ¹ is greater or equal than that in Γ².

Axiom 1 captures the idea of significantly sized groups through the concept of network components and their relative size. Each component represents a different social group. The fact that, by definition, there are no links at all between components represents the idea of maximum distance between the groups or between-group heterogeneity. This axiom focuses on the cardinality or relative size of the first two largest components taking account of the first pre-requirement in the previous definition of polarization (There must be a small number of significantly sized groups.) In fact, the axiom establishes that the greater the size of at least one of the two largest components, other things being equal, the larger the degree of polarization.

Axiom 2 Maximum amount of polarization. Let be such that are the only two cliques of Γ with relative size equal to a half i.e. for any .

Axiom 2 captures the idea of a society divided only into two groups of equal size (each of them equal to a half) with the largest distance among them and with all individuals in each group having communication among them (represented by means of completely connected components or cliques). Such a society exhibits the maximum amount of polarization.

Axiom 3 One component networks exhibit minimal polarization.

Axiom 3 focuses on cases where society can be seen as having only one social group in the sense that everyone communicates with each other directly, they share some affiliations, or indirectly, they communicate through someone else.

Clustering Polarization

The idea of clustering polarization is based on the idea of identification or within-group homogeneity, the second pre-requirement in the previous definition of polarization. Other things being equal, the greater the feelings of identification among the members of the group, the greater the level of polarization. Thus, I base this clustering polarization preorder in the network-theoretic notion of overall clustering or clustering coefficient of the components (definiton 8 in the previous section).

As before, it is noteworthy that the fact that, by definition, there are no links at all between components represents the idea of maximum distance between the groups or between-group heterogeneity, the third pre-requirement in the previous definition of polarization.

The following axioms define clustering polarization:

Axiom 4 Consider any two networks with the same population i.e. N¹=N² and let be the set of ordered components of network i, ordered in terms of size from higher to lower. Then,

Axiom 4 captures the idea of within-group homogeneity through the concept of overall clustering. The intuition behind overall clustering is the following: first, we considered the total number of pairs of nodes jk, that presented a link with a common third node i. Then, we looked at how many of those pairs jk, are actually connected to wach other. If we repeat the exercise for all of i, then we have the overall clustering of the network. Thus, the axiom focuses on within-group homogeneity by measuring how tightly clustered individuals are within each of the two largest components. Therefore, other things being equal, the higher the overall clustering coefficient of the components the higher the degree of polarization.

Axiom 5 For networks with only one component then if and only if has greater clustering coefficient.

Axiom 5 is a refinement for networks with only one component. The network with the greater clustering coefficient or within group homogeneity is considered less polarized, people communicate more with each other.

Let H = (V, E) be a social affiliation hypergraph where V = {v₁,..., v_n} denotes the finite set of individuals in society and the set E = {e₁,..., v_m} denotes the set of all possible affiliations in that society.

For each is the set of all non trivial affiliations, E_k (i.e. affiliations with cardinality greater than 2, #e≥2) such that individual i belongs to them.

Each individual is assumed to have a binary dichotomic system of preferences. A binary system of preferences is dichotomic if and only if there is a partition of P(E) (the power set of E) such that for 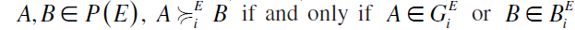, or both. Here, G_i represents the set of affiliations considered by individual i as "good" affiliations and B_i represents the set of affiliations considered by individual i as "bad" affiliations. First, it is assumed that preferences can be either "upward" or "downward" monotonic.

Preferences are "upward" monotonic if and only if they are dichotomic and there exist 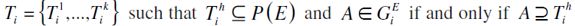for some h',h'=k,...,1.

Preferences are " downward" monotonic if and only if dichotomic and there exist for some h',h'=k,...,1.

This monotonic structure of preferences implies that supersets of belong to the set G_i, i.e. to the set of affiliations considered by i as "good." This property can miss a real and important issue. Consider, for instance, that one affiliation in the affiliation set X is that of belonging to a mafia. Under the monotonic assumption, as far as , meaning that i establishes a tie with j without any consideration about the fact that j is part of the mafia! Of course, this is unrealistic. In order to cope with this real and important issue, we also modeled preferences in an alternative "mixed" non-monotonic way.

Preferences are "mixed" non-monotonic if and only if dichotomic and there exist if and only if there exists and for all m=1,...,k.

Finally, we assume that any social system induces a communication network (graph) Γ(H). Specifically, given a social system then, for all .

If there is no link among individuals i and j then, it is assumed that individuals either do not know each other or they are not able to cope with their different affiliations sets in order to establish communication. In any of both cases and to simplify matters, the result is the same; they feel separate from one another.

In this section, we analyze how changes in the affiliation sets for each individual and changes in social preferences may alter the degree of social polarization. Specifically, we focus on how expansions of the affiliations sets of each individual affect polarization under the three different types of preferences proposed in the model i.e. upward and downward monotonic, and mixed non-monotonic preferences. Additionally, we also analyze how such an expansions alter polarization for centralized societies, characterized here by hypergraphs called "stars."

Proposition 1 Let H=(V,E) be a social affiliation hypergraph with "upward monotonic" dichotomic preference profile and with systems of thresholds given by . Then, for any if and only if there exist such that .

Proof. Suppose ij∈Γ(H) then by definition i.e. there exist. Hence, .

Proposition 1 shows that with upward monotonic dichotomic preferences, two individuals communicate if and only if they share at least one affiliation of those who individually they consider as good or desirable affiliations in order for them to establish communication.

Proposition 2 Under "upward monotonic" dichotomic preferences , with systems of thresholds given by for each then .

Proof. If ij∈Γ(H) then, there exist. Hence .

Proposition 2 shows that if there is an expansion of each individual affiliations set, then, under upward monotonic dichotomic preferences, the new associated communication graph-after expansion-must include the initial one. The intuition is that if all individuals expand their affiliation sets then there would be more, or at least the same, communication links among individuals in society.

Proposition 3 Under "upward monotonic" dichotomic preference profile , with systems of thresholds given by for each , for each i ∈ V then .

Proof. If for 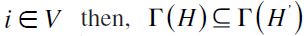(Proposition 2). Hence, there exists at least one . Therefore, , according to the component-size polarization (Axiom 1). The cardinality of one of the greatest components in H' will be less than that in H.

Proposition 3 shows that under upward monotonic dichotomic preferences, one graph is less polarized than the other if the affiliation sets of the former (one for each individual) includes the affiliation sets of the latter. The intuition grounds on the previous result, if all individuals expand their affiliation sets, then, there would be more, or at least the same, communication links among individuals in the new society. Therefore, other things being equal, there would be more communication among individuals who did not communicate before and as a consequence, the graph will be less polarized.

Proposition 4 Under "downward monotonic" dichotomic preferences , with systems of thresholds given by for each then i.e. if each player's set of affiliations is extended, then the resulting communication graph shrinks.

Proof. If then, there exist. Hence,.

Proposition 4 shows that, under downward monotonic dichotomic preferences, if there is an expansion of each individual's affiliations set then, the new associated communication graph-after expansion-must be included in the initial one. The intuition behind the proof is that if all individuals expand their affiliation sets, then, there would be less, or at least the same, communication links among individuals in society.

Proposition 5 Under "downward monotonic" dichotomic preferences , with systems of thresholds given by for each then .

Proof. If (Proposition 4). Hence there may exist at least one . Therefore,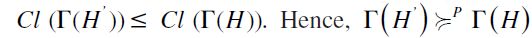, according to the component size polarization (Axiom 1). The cardinality of one of the greatest components in H' will be greater than that in H.

Proposition 5 shows that under downward monotonic dichotomic preferences, one graph is more polarized than the other, if the affiliation sets of the former (one for each individual) include the affiliation sets of the latter. The intuition grounds on the previous proposition, if all individuals expand their affiliation sets, then, there would be less, or at least the same, communication links among individuals in the new society. Therefore, other things being equal, there would be less communication among individuals than before and, as a consequence, the graph would be more polarized.

Proposition 6 Under "mixed non-monotonic" preferences with system of thresholds and ceilings , if then, the resulting communication graph Γ(H') may grow larger, shrink, or stay the same with respect to H().

Proof. and will grow larger than Γ(H). If for at least one m=1,...,k. Hence, Γ(H') will shrink with respect to Γ(').

Proposition 6 shows that under non-monotonic preferences systems, an expansion of the affiliations set will alter the resulting communication network in different ways depending on the preferences themselves. Thus, the possibility for new social relationships depends crucially on the set of affiliations considered as good or bad for each individual.

The next two propositions focus on "Stars" one relevant type of hypergraphs (societies). More precisely, centralized societies i.e. societies characterized by the existence of one individual who shares at least one affiliation with everyone else so she is at the center of society. It must be noted that stars are networks characterized by the fact that they have only one component.

Proposition 7 If H=(V,E) is a star, and an "upward monotonic" dichotomic preference profile with systems of thresholds given by . Then, Γ(H) is connected.

Proof. Let be the star-center. Since, by definition, for all then, there exist. Hence, and i.e. there is a path from i to j and Γ(H) is connected.

Proposition 7 shows that under upward monotonic dichotomic preferences, the communication graph associated to a centralized society will always be connected. In other words, there is either direct or indirect communication between two individuals in society. Intuitively, if everyone communicates with the same person (the star center), then it is always possible for any two people to communicate through her.

Proposition 8 Under " upward monotonic" preferences, with systems of thresholds given by , H'=(V,E') are 2 stars such that , then, .

Proof. Let i* ∈ V be the star-center. Since, by definition, for all then, there exist. Hence, the degree of i* equals n-1 for any star. Therefore, if for all h,k then, there exists at least 1 pair ij such that . Thus, there is at least one x such that . So, because the clustering coefficient in Γ(H) will be greater than that in Γ('H) and, therefore, according to clustering polarization (Axiom 5) Γ(H) is less polarized thanΓ('H).

Proposition 8 shows that under upward monotonic dichotomic preferences, if the cardinality of all hyperlinks is greater in one hypergraph than in another, then, the former will be less polarized. The intuition behind this result is that the more people share common affiliations, the more communication there will be among them and, therefore, society will be less polarized.

As explained above, polarization is highly correlated with social conflict. The model presented here may contribute to the analysis of social conflict in at least two respects. First, the explicit recognition of the fact that individuals have multiple affiliations overcomes the usual problem in economics of analyzing polarization in terms of just one dimension. In fact, proposition 1 deals with the issue that most of the time people establish social relationships after finding a certain amount of commonalities with each other. Propositions 2 and 3 recognize the fact that, under upward monotonic preferences, people with longer sets of affiliations would have more opportunities to find things in common with others, thus, abating the sense of antagonism and, diminishing social polarization. As an example, consider a Hutu in Kigali whose sense of identity is based on the only fact of being a Hutu. Thus, for him, it may be easier to consider a Tutsi as his enemy. But, recognizing the fact that he is not only a Hutu but also an habitant of Kigali, a citizen of Rwanda an African and a human being enables him to find some commonalities with a Tutsi.

Second, the model also accounts for the fact that certain affiliations considered undesirable affiliations may block any social relationship. There is an old Italian tale about the rise of Fascism in the Twenties. A Fascist recruiter was trying to convince a socialist peasant to join the party. The peasant said: "I cannot join your party. My father was socialist and so was my grandfather so it is impossible for me to become a Fascist." The recruiter responded: "Your reasoning is all wrong. What if your father and grandfather had both been assassins?" The peasant answered: "Ah, in that case, I would surely join the Fascist party." Propositions 4 and 5 show that under downward monotonic preferences, if a person considers certain affiliations as bad or undesirable and finds at least one of them in someone's else affiliation set, then, there is no room for establishing communication, independently of the number of commonalities they may have and, as a consequence, polarization increases.

Proposition 6 shows that under a non-monotonic system of preferences, an expansion of the affiliations set will alter the resulting communication network in different ways depending on the preferences themselves. Thus, the possibility of new social relationships depends crucially on the set of affiliations considered as good or bad by each individual.

Propositions 7 and 8 show that for centralized societies, the greater the number of people sharing each affiliation, the less the polarization. It remains for further research to explore, among other questions, how changes in the affiliation sets modify the resulting communication graphs for different well known types of hypergraphs such as bipartite hypergraphs.

2 The book by Jackson (2008) is a good book for the reader interested into the theory of social networks.

[1] Esteban, J., & Ray, D. (1994). On the measurement of polarization. Econometrica, 62, 819-851.         [ Links ]

[2] Esteban, J., & Ray, D. (1999). Conflict and distribution. Journal of Economic Theory, 87, 379-415.         [ Links ]

[3] Gasparini, L., Horenstein, M., Molina, E., & Olivieri, S. (2008). Income polarization in Latin America: Patterns and links with institutions and conflict. Oxford Development Studies, 36(4), 461-484.         [ Links ]

[4] Huntington, S. (1996). The clash of civilizations and the remaking of the world order. New York: Simon & Schuster.         [ Links ]

[5] Jackson, M. (2008). Social and economic networks. Princeton: Princeton University Press.         [ Links ]

[6] Montalvoa, J., Reynal-Querol, M. (2003). Religious polarization and economic development. Economics Letters, 80, 201-210.         [ Links ]

[7] Reynal-Querol, M. (2002a). Ethnicity, political systems, and civil wars. Journal of Conflict Resolution, 46, 29-54.         [ Links ]

[8] Reynal-Querol, M. (2002b). A contribution on the measurement of religious diversity. PRPES Working Paper 4. Wheatherhead Center for International Affairs, Harvard University.         [ Links ]

[9] Sen, A. K., & Foster, J. E. (1997). On economic inequality (2nd ed.). Oxford: Clarendon Press.         [ Links ]

[10] Sen, A. K. (2006). Identity and violence. New York: W.W. Norton & Company        [ Links ]