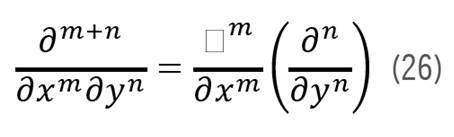1. INTRODUCCIÓN
La predicción exacta de propiedades ópticas no lineales (NLO, siglas en inglés de Non Linear Optics) mediante métodos mecanocuánticos permite el diseño racional de nuevos materiales, así como una comprensión de la relación entre estas propiedades y la estructura química del material [1]. Existen dos métodos basados en mecánica cuántica para ello [2,3]: método de perturbaciones acopladas (CP, siglas en inglés de Coupled Perturbed methods) y diferencias finitas (FF, siglas en inglés de Finite Field). Ambos métodos permiten el cálculo de propiedades NLO mediante la diferenciación de la energía de la molécula con respecto al campo eléctrico aplicado. En el primero, se aplica un tratamiento perturbativo de primer orden al sistema, la perturbación es un campo eléctrico uniforme, y se obtienen las derivadas a partir de las expresiones analíticas explícitas [3]. Generalmente este método tiene una alta precisión numérica y es computacionalmente eficiente. Sin embargo, su implementación en nuevas aproximaciones mecanocuántica es difícil.
El método FF propuesto por Kurtz y col. [4], y Maroulis [5] se basa en la aplicación del método de diferencias finitas al cálculo de NLO. El FF es un método sencillo y fácil de aplicar, donde sólo es necesario el valor de la energía en ciertas intensidades de campo sin información adicional acerca de estados excitados.
Todo lo anterior sumado a su capacidad actualización y reformulación hacen del FF un método universalmente aplicable a cualquier nivel de la teoría, con el único requisito de que un programa de química cuántica permita expresar el campo eléctrico en el hamiltoniano. Las desventajas para el FF se centran en su baja eficiencia computacional y la limitada precisión numérica.
Ambas metodologías se han utilizado exitosamente en la predicción de propiedades ópticas lineales y no lineales de moléculas orgánicas [1,6] e inorgánicas [7]. Sin embargo, la exactitud de los resultados depende de varios factores, entre estos el tamaño del sistema y la correlación electrónica. Los resultados del diseño de materiales sugieren que las moléculas con posibles aplicaciones reales son de gran tamaño, es decir, moléculas con un gran número de átomos [8,9], oligómeros, polímeros [10], cristales, entre otros. Por otro lado, la correlación electrónica tiene un efecto significativo sobre el valor de las propiedades ópticas no lineales. Ambos factores aumentan el costo computacional y el tiempo de cálculo.
En consecuencia, los métodos basados en la teoría del funcional de la densidad [DFT, siglas en inglés de Density Functional Theory] han ganado popularidad en reducción de estos problemas. El creciente y rápido desarrollo de funcionales para aplicaciones diversas genera un retraso en la actualización del algoritmo CP, permitiendo que el método FF sea la opción viable para el cálculo de NLO. En este sentido, es necesario diseñar nuevos métodos y/o algoritmos de diferencias finitas de fácil implementación que permitan el cálculo de las propiedades ópticas no lineales con mayor exactitud.
En los últimos años, se han propuestos algunas ecuaciones que generalizan las expresiones de diferencias finitas basadas en la serie de Taylor que permiten obtener derivadas numéricas de grado y exactitud arbitrarias. Las expresiones reportadas se obtuvieron aplicando diversos métodos para resolver el sistema de ecuaciones que se plantea en el problema de diferencias finitas, por ejemplo, método de Cramer [11-14], o por inversión de la matriz del sistema [15-17]. Todos los autores aseguran que los resultados obtenidos con las ecuaciones propuestas son más exactos que aquellos obtenidos con las ecuaciones clásicas [11-17].
Considerando lo antes expuesto, en este trabajo se dedujeron un conjunto de ecuaciones generalizadas de diferenciación numérica por el método de diferencias finitas basadas en series de Taylor para el cálculo de NLO de moléculas tomando como punto de partida los nuevos esquemas planteados en la literatura [11-17]. A partir de las mismas se calcularon las propiedades ópticas no lineales de 2 bencenos para-disustituidos con grupos donores y aceptores de densidad electrónica cuyos valores de primera y segunda hiperpolarizabilidad están reportados por Cheng y col. [18]. Las moléculas que se estudiaron son la p-nitroanilina y el p-cianofenol.
2. TEORÍA
2.1 Teoría óptica
Cuando un campo eléctrico F de alta intensidad (por ejemplo, un láser) incide sobre una molécula, ésta se polariza produciendo una redistribución de cargas que origina una polarización inducida P(F) asociada a un momento dipolar inducido µ(F). La frecuencia y la fase presentan alteraciones, provocadas por los fenómenos ópticos no lineales. La dependencia no lineal del momento dipolar inducido con respecto al campo se expresa en función de una serie de Taylor:
El primer término, µ0, es el momento dipolar intrínseco de la molécula en ausencia del campo eléctrico. El segundo término, 𝛼ij, es el tensor de la polarizabilidad lineal. El tercer y cuarto término 𝛽ij y Yijkl son las hiperpolarizabilidades de primer y segundo orden, respectivamente. Ambos coeficientes son tensores, es decir, son dependientes de la dirección de emisión de onda incidente. Los subíndices i, j, k y l, representan los ejes del sistema de coordenadas cartesianas de la molécula.
La ecuación 1 se puede expresar como una función de la energía [3]:
donde E0 es la energía del sistema en ausencia del campo eléctrico, y los coeficientes de la ec. 2 están definidos por:
Estos resultados, en muchos casos se deben comparar con resultados obtenidos en los experimentos. En este sentido, es necesario calcular a partir de estos valores, regularmente obtenidos de cálculos teóricos, las cantidades derivadas que son susceptibles a comparación con el experimento. La expresión utilizada en la polarizabilidad de primer orden 𝛼𝛼 es conocida como la polarizabilidad promedio, y está dada por la ecuación:
Para 𝛾, la expresión 5 permite determinar un promedio de todas las componentes de la propiedad, y se utiliza en el experimento de generación de terceros armónicos [7,19,20]:
En el caso de la respuesta óptica no lineal de segundo orden o la primera hiperpolarizabilidad la cantidad experimental depende del proceso óptico con el cual se desea comparar. Cuando la respuesta no lineal consiste en la generación de segundos armónicos, la respuesta total viene dada por:
2.2 Método de campo finito
Las ecuaciones de campo finito están conformadas por las expresiones matemáticas para calcular las propiedades ópticas: momento dipolar (μ), polarizabilidad (μ), primera y segunda hiperpolarizabilidad, β y γ, respectivamente. Se han planteado 2 conjuntos de ecuaciones: las ecuaciones de Kurtz y col. [4], y las ecuaciones de Kamada y col. [21]. En el primer conjunto, se aplicaron campos desde -2F hasta 2F a lo largo de los ejes coordenados (x, y y z) en la serie de Taylor de la ecuación 2. Al resolver el sistema de ecuaciones lineales se obtienen las componentes axiales de las propiedades antes mencionadas, aquí mostramos las correspondientes a las hiperpolarizabilidades:
donde 𝐸(𝐹) es la energía del sistema con un campo aplicado F a lo largo del eje i ( ∀𝑖 = 𝑥, 𝑦, 𝑧 ). El valor (0) representa la molécula sin campo aplicado.
Las componentes no-axiales, derivadas mixtas, se obtuvieron aplicando un campo entre los ejes. La expansión en serie de Taylor de la ecuación 2 queda,
Considerando las energías para los campos: (Fi,Fj), (-Fi,Fj), (Fi,-Fj) y (-Fi,-Fj), los autores obtienen:
Estas ecuaciones permiten el cálculo de las cantidades susceptibles a ser comparadas con las mediciones experimentales: segunda hiperpolarizabilidad promedio (ecuación 5) y primera hiperpolarizabilidad total, βtot .
Kamada y col. [21], propuso otro conjunto de ecuaciones aplicando campos desde -3F hasta 3F con un tamaño de paso igual a F. El propósito es obtener valores de propiedades con un error 2 órdenes de magnitud menor que las ecuaciones de Kurtz y col. [4]. Así las ecuaciones obtenidas fueron:
3. METODOLOGÍA
Las moléculas que se estudiaron son la p-nitroanilina y el p-cianofenol y se ubicaron en los ejes coordenados de acuerdo con el orden de prioridad dado por su simetría, como se muestra en la figura 1. El origen del sistema de coordenadas coincide con el centro de masa de la molécula. La energía se calculó resolviendo las ecuaciones de Kohn y Sham, en el marco de la Teoría del Funcional de la Densidad, DFT.
Se utilizaron los siguientes funcionales: con corrección para largo alcance ωB97, LC-ωPBE y HSEH1PBE, con corrección por atenuación coulómbica, CAM-B3LYP, con corrección por dispersión ωB97XD, y la familia de funcionales de Thrular, M11, N12SX y MN12SX. En todos los casos se calcularán las hiperpolarizabilidades de primer y segundo orden, obtenidas con (1) ecuación de diferencias finitas de Kurtz y col. [4], (2) ecuación de diferencias finitas de Kamada y col. [21], y (3) con el conjunto de ecuaciones a deducidas en este trabajo. Los cálculos se realizaron con el programa Gaussian 09 [23]. Se utilizó el conjunto base 6-311++g(3d,3p).
4. RESULTADOS Y DISCUSIÓN
4.1 Ecuaciones generalizadas para hiperpolarizabi lidades
Con el nombre de ecuaciones generalizadas se conocen aquellas que pueden calcular las derivadas con exactitud y precisión arbitrarias. Las mismas deben incluir, además de las derivadas m-ésima en una variable, las derivadas mixtas. Los primeros intentos por generalizar las ecuaciones de diferencias finitas son los reportados por Khan y Ohba [11-14] y Li [15]. Sin embargo, son Albadarneh y col. [16], quienes presentaron y demostraron una ecuación generalizada para las expresiones de diferencias finitas. La expresión para la derivada m-ésima de x en el punto s para n + 1 puntos es:
donde j, l, s = 0 … n.an-1,s,j es el operador recursivo definido por Li [15]:
La aplicación de esta ecuación para las hiperpolarizabilidades axiales genera las mismas ecuaciones de Kurtz y col. [4], y Kamada y col. [21]. Si n = 5, se obtienen las primeras ecuaciones 7 y 8. Las últimas se obtienen para n = 7, ecuaciones 12 y 14. En ambos casos, s = 0 considerando que j va desde −(n − 1)/2...0...(n − 1)/2. Con el fin de tener una referencia más exacta de la derivada m-ésima, en este trabajo se obtuvo la ecuación de diferencias centrales para β y γ axiales, considerando 9 puntos igualmente espaciados:
aquí se utiliza la misma nomenclatura que en las ecuaciones 7, 8, 12 y 14.
Para las hiperpolarizabilidad entre de los ejes, partimos de la ecuación generalizada de Albardaneh y col. [16], para derivadas parciales:
Partiendo de puntos igualmente espaciados y considerando los campos aplicados en los métodos de Kurtz y col. (4), y Kamada y col. (21), es decir, campos dobles (2F) y triples (3F) en las direcciones i y j se obtuvieron las siguientes ecuaciones para β:
Con el mismo procedimiento se obtuvieron las ecuaciones para la segunda hiperpolarizabilidad para ambos campos:
Las ecuaciones mostradas anteriormente no son únicas. La generalización de la ec. 16 permite la obtención de ecuaciones particulares para la precisión y exactitud deseada.
Las diferencias entre las ecuaciones presentadas en este trabajo y las ecuaciones de Kurtz y col. (4), y Kamada y col. (21), radican esencialmente en la distribución de la rejilla. La figura 2 muestra las diferentes configuraciones de rejilla para las ecuaciones de Kurtz y col. [4], (fig. 2a) y para la ec. 22 (fig. 2b). En este orden de ideas, la misma figura muestra las rejillas correspondientes a la ecuación de Kamada y col. [21], y la obtenida en este trabajo para campos triples (ver figuras 2c-d).
Cada configuración contiene un error asociado al truncamiento en la serie de Taylor. Por ejemplo, las componentes axiales de las hiperpolarizabilidades en las ecuaciones de Kurtz y col. [4], tienen un error de truncamiento asociado proporcional a O(F2). Mientras que en las ecuaciones de Kamada y col. [21], el error es proporcional a O(F4).
En el caso de las componentes axiales el error asociado es la suma de los errores asociados a las componentes axiales. Es decir, en el esquema de las diferencias finitas, una derivada parcial se obtiene combinando las derivadas unidimensionales [23]:
donde m, n es el orden de las derivadas, y x, y las variables.
De acuerdo con esto, el error asociado se propaga como la suma de los errores de las derivadas unidimensionales [23,24]. Siguiendo este esquema, las ecuaciones 10 y 11 tienen un error de truncamiento asociado de O (Fi+Fj) (Kurtz y col. [4]) y las ecuaciones 13 y 15 de O (Fi+Fj) (Kamada y col. [21]).
En este punto se refleja una diferencia de un orden de magnitud entre las componentes axiales y no axiales para cada esquema. Esta diferencia provoca un desbalance en la incertidumbre de las cantidades susceptibles de ser comparadas con el experimento. Por ejemplo, para la comparación con los experimentos de Hyper-Rayleigh Scattering, el cálculo de requiere el cálculo de (βzzz) y (βxzz). Ambas ecuaciones contienen una mezcla de componentes axiales y no-axiales. En consecuencia, el error asociado está dominado por la contribución del término no-axial que es un orden de magnitud mayor. En este sentido, se está realizando un esfuerzo innecesario en el cálculo de la magnitud axial. Por el contrario, las ecuaciones obtenidas en este trabajo mantienen un balance en los errores de truncamiento, así el error asociado es el mismo para las componentes axiales como las no axiales.
4.2 Primera hiperpolarizabilidad de sistemas moleculares
La tabla 1 muestra los resultados de las componentes del tensor de hiperpolarizabilidad calculados con las ecuaciones 7 y 12, y para campos igual a 4F para la molécula p-nitroanilina. Al aumentar la magnitud del campo aplicado las componentes axiales disminuyen, al igual que las componentes no-axiales, pero en menor proporción. Una comparación entre los funcionales muestra el siguiente orden: M11 < ωB97 < ωB97XD < CAM-B3LYP < MN12SX < HSEH1PBE < N12SX. El funcional LC-ωPBE mostró un comportamiento atípico. Los resultados revelaron un comportamiento quasi-esférico de la respuesta electrónica, que no se observa experimentalmente. Esto demuestra una mala descripción de la densidad electrónica por el mencionado funcional, debido a una notoria sobreestimación de los valores no axiales.
La diferencia entre los resultados de βxxz y β yyz con método de Kurtz y col., [4], y la rejilla 2F oscila entre 0,01 y 0,14 %, mientras que los resultados de Kamada y col. [21], con respecto a 3F está en el rango de 0,004 a 0,068 %. Esta comparación revela que la contribución de los valores de la energía en las esquinas de la rejilla del campo 2F tiene un efecto significativo sobre la componente axial de la hiperpolarizabilidad (ver figuras 2a-b). Por el contrario, en la rejilla 3F, la mayor presencia de los valores en las regiones centrales de la rejilla provoca una disminución de la contribución de los valores de las esquinas (ver figuras 2c-d). En consecuencia, las diferencias para una rejilla mayor deben ser menor, como se obtuvo en este trabajo. El menor efecto se observó con el funcional ωB97, mientras que, CAM-B3LYP mostró la mayor diferencia.
La p-nitroanilina se ha estudiado profundamente desde el punto de vista experimental y teórico. Existen numerosos reportes de las NLO de la misma, y se muestran los más relevantes en la tabla 1. Al comparar estos resultados, se observó que los resultados presentados en este trabajo tienden a subestimar los valores típicos obtenidos con DFT, tanto para las componentes axiales como no-axiales. Sin embargo, están muy cercanos a los valores ab initio, es decir MP4 [25] y CCSD [26], aceptados como referencia comparativa para los cálculos teóricos.
Los valores MP2 y MP4, reportado por Urdaneta y col. [25], con el mismo conjunto base que se utilizaron en este trabajo, están sobrestimados. Este comportamiento posiblemente es el resultado de la aplicación de campos altos (0,005 ua) por parte de Urdaneta y col. [25], que pueden provocar la aparición de estados electrónicos cercanos y diferentes al estado fundamental. Los métodos que tienen un mejor desempeño vienen dados por los funcionales HSEH1PBE y N12SX con un error relativo con respecto al valor CCSD/aug-cc-pVTZ [26] de 5,1 y 6,9 %, respectivamente. Las componentes no-axiales de la hiperpolarizabilidad mostraron comportamientos similares a los valores reportados para métodos ab initio, es decir, βzzz > βyyz > βxxz. Los reportes basados en DFT revelan que la respuesta en los ejes XZ es igual a la respuesta YZ. Esto revela simetría en la densidad electrónica de los ejes mencionados. La simetría C2v de la p-nitroanilina, sugiere un comportamiento similar al mostrado por los resultados ab-initio, y los reportados en este trabajo.
El resultado experimental reportado en la bibliografía se basa en EFISHG [27]. El autor reporta el valor de β||, que para una molécula orientada con el momento dipolar es igual a. De esta manera, el valor de obtenido a partir del valor de β|| es 1787 ± 73 ua, como se muestra en la tabla 1. Según este valor, el mejor desempeño se obtuvo para los funcionales HSEH1PBE y N12SX, con 0,8 y -1,1 % respectivamente. Garza y col. [28], compararon una serie de funcionales corregidos por largo alcance para la evaluación de la hiperpolarizabilidad. El autor concluye que los funcionales HSE, generan resultados comparables con el valor de referencia CCSD. Los resultados obtenidos en este trabajo soportan las conclusiones de Garza y col. [28]. Es necesario resaltar que, hasta donde se tiene conocimiento, este trabajo reporta el primer valor de hiperpolarizabilidad de p-nitroanilina con el funcional N12SX.
El p-cianofenol no se ha calculado teóricamente, y la medida experimental que existe se realizó con el p-metoxicianofenilo. El comportamiento de las componentes axiales y no-axiales de la primera hiperpolarizabilidad sigue el patrón observado para la p-nitroanilina (ver tabla 2). Sin embargo, la dirección de la respuesta frente al campo es distinta a la molécula predecesora. En este caso, el momento dipolar se orienta hacia el eje y, por tanto, la respuesta mayoritaria se espera en esa dirección. Existe una respuesta importante en x, debido al flujo de densidad electrónica a lo largo del anillo. A partir de estos resultados, observamos que la eficiencia de este material para la respuesta no lineal de primer orden es un orden de magnitud más baja que para la p-nitroanilina.
Al comparar los resultados obtenidos en este trabajo, con los obtenidos por Cheng y col. [18], se obtuvieron errores relativos entre 5,5 y 30 %. El mejor desempeño se observó para el funcional MN12SX. Es necesario acotar que se excluyó el resultado LC-ωPBE debido a inconsistencia en los resultados de las componentes no-axiales. El resto de los funcionales mostraron comportamientos similares. Estas altas diferencias se deben principalmente al efecto del grupo metilo y en segundo lugar a la orientación molecular frente al momento dipolar.
4.3 Segunda hiperpolarizabilidad de sistemas moleculares
Las componentes del tensor de segunda hiperpolarizabilidad para la p-nitroanilina se muestran en la tabla 3. El efecto del tamaño del stencil es mayor que para la primera hiperpolarizabilidad, aproximadamente 0,4 % en la componente axial y 0,6 % para las no axiales.
En términos generales se observó una subestimación de los valores de la segunda hiperpolarizabilidad al compararlos con los valores reportados. Urdaneta y col. [25], presentaron la segunda hiperpolarizabilidad con los métodos MP2, MP4 y CAM-B3LYP con el conjunto base 6-311++g(3d,3p). Los resultados obtenidos en este trabajo mostraron entre un 40 y 53 % de diferencia con respecto a los valores MP2 y MP4, y entre 24 y 31 % con respecto al valor CAM-B3LYP. Estas diferencias se pueden atribuir a la intensidad del campo aplicado. Urdaneta y col. [25], utilizaron 0,005 ua mientras que en este trabajo se usó 0,001 ua. Sin embargo, es necesario hacer un estudio detallado de la influencia del campo sobre la hiperpolarizabilidad considerando el estado de la molécula. Esta tendencia se mantiene para los resultados de γave.
El valor experimental, obtenido mediante la técnica EFISHG, y reportado por Cheng y col. [18], es 29,809 ua. El funcional CAM-B3LYP generó el valor más cercano a la propiedad experimental con 35 % y el resto de funcionales se diferencian por alrededor de 40 %. Es necesario menciona que la segunda hiperpolarizabilidad experimental está influenciada por otros factores que no se consideran en el cálculo teórico: contribución vibracional, efecto del disolvente, entre otros.
En el caso del p-cianofenol, los errores relativos con respecto al valor experimental fueron menores que los observados para la molécula anterior. Entre 10 y 30 %, siendo los funcionales HSEH1PBE, N12SX y MN12SX los de mejor desempeño con ≈ 10 %, y 16-17 %, respectivamente (ver tabla 3). Este resultado sigue la tendencia mostrada por la primera hiperpolarizabilidad para las moléculas estudiadas.
5. CONCLUSIONES
En este trabajo se hizo un estudio de las ecuaciones de diferencias finitas para el cálculo de propiedades ópticas no lineales de las moléculas p-nitroanilina y el p-cianofenol. A partir de las ecuaciones generalizadas se obtuvieron un nuevo conjunto de ecuaciones que regularizan el desbalance en la rejilla de cálculo observado en las ecuaciones utilizadas tradicionalmente. Las nuevas ecuaciones regularizan el término residual. Los resultados muestran que las ecuaciones generan resultados similares o mejores que aquellos obtenidos por las ecuaciones tradicionales. Las ecuaciones se probaron sobre un conjunto de moléculas con características donor-aceptor. Los resultados mostraron que los funcionales que contienen una alta contribución de corto alcance mostraron un mejor desempeño para la predicción de propiedades ópticas no lineales de moléculas con una alta transferencia de carga. Los funcionales con mejor desempeño fueron HSEH1PBE, N12SX y MN12SX.