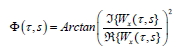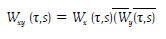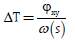Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
INTRODUCCIÓN
Son numerosas las explicaciones dadas en la literatura económica a la creciente expansión del sector público en los países de la OCDE y, en particular, en España. El período después de la Segunda Guerra Mundial vio una fuerte expansión en el gasto público, en el espíritu del Estado del bienestar postulado por Keynes y Beveridge. El análisis de las causas o factores determinantes de este incremento ha sido la fuerza dirigente detrás del trabajo y la preocupación de numerosos investigadores en muchos países de todo el mundo y, por encima de todo, en la OCDE. Las explicaciones resultantes son diversas, pero una de las más referenciadas por los investigadores es la conocida como ley de Wagner, que propone una relación de causalidad entre gasto público y renta. La ley de Wagner está basada en una relación secular, lo que significa que su contrastación empírica debe ser llevada a cabo en un contexto de largo plazo en el que se producen cambios en las condiciones políticas y económicas.
La ley de Wagner provocó un gran interés entre los economistas del sector público desde su redescubrimiento gracias a la recopilación Classics in the Theory of Public Finance por Musgrave y Peacock (1958) . Su propia formulación ha sido (y continúa siendo) debatida, dada la ambigüedad del trabajo de Wagner y continúa siendo contrastada una y otra vez tanto en países desarrollados como subdesarrollados y en desarrollo. El análisis empírico de la ley ha evolucionado en paralelo con el desarrollo y conocimiento de las técnicas econométricas de tal forma que los avances econométricos más sofisticados han sido utilizados para llevar a cabo su contrastación.
En este trabajo se realiza una contrastación empírica de la ley considerando dos metodologías alternativas. Por una parte la econometría de series temporales y por otra la metodología wavelet que no ha sido utilizado anteriormente para el caso español1. En el primer caso, podemos considerar un número limitado y conocido de antemano de cambios estructurales en los datos, mientras que la segunda metodología no limita el número de rupturas y se obtienen las mismas simultáneamente a los resultados. En nuestra opinión ambas metodologías tienen sus ventajas e inconvenientes. Mientras la primera nos permite precisar los resultados y considerar diferentes formas funcionales, la segunda solo nos permite dos formas funcionales. Por otra parte, mientras la primera limita el número de rupturas, en la segunda aparecen las rupturas junto con el resultado. Los resultados difieren en ambas metodologías. En la primera no se puede rechazar la ley de Wagner para la totalidad de la muestra, incluyendo en la ecuación de cointegración y en el MCE las rupturas estructurales, mientras que en la segunda la precedencia del gasto con respecto al PIB y viceversa no permite afirmar el cumplimiento de la ley salvo en períodos de tiempo muy cortos. Por ello, y con carácter general, se puede rechazar la ley para el período completo.
El trabajo aporta dos contribuciones a la literatura sobre la ley. En primer lugar, se considera un largo período de tiempo, 1850-2016, lo que hace necesario tener presentes los posibles cambios en la economía y en la evolución del gasto público. Este análisis se realiza teniendo en cuenta las posibles rupturas estructurales en las series y aplicando la metodología de raíces unitarias y cointegración con rupturas estructurales. En segundo lugar, se comparan los resultados obtenidos utilizando dos metodologías completamente diferentes. Este tipo de análisis solo tiene el precedente de Funashima (2017) , aunque dicho autor pone especial énfasis en el análisis wavelet, mientras que en este caso se realiza un análisis equilibrado de ambas metodologías. Nuestro objetivo fundamental es analizar la fragilidad de la formulación de la ley de Wagner cuya refutación o no depende en gran medida de la metodología utilizada y del período de análisis considerado.
En la siguiente sección se presenta de manera muy resumida la ley de Wagner y las contrastaciones empíricas más recientes. En la segunda se realiza una breve semblanza del gasto público y el crecimiento económico en el período 1850-2016. En la tercera se presentan los datos y se realiza el análisis empírico utilizando la metodología econométrica habitual, mientras que en la cuarta se utiliza metodología wavelet. En la quinta se presentan las conclusiones.
1. LA LEY DE WAGNER
Wagner formuló su hipótesis o ley basándose en la observación de la realidad: “la ley de la creciente expansión de las actividades públicas, en particular las estatales se convierte para la economía fiscal en la ley de la creciente expansión de los requerimientos fiscales. Los requerimientos del Estado crecen así como los de las autoridades locales” (Wagner, 1958, p. 8). Interpretada desde el punto de vista económico-político, esta ley expresa la absoluta, y también relativa, extensión de la estructura de la organización publica junto con, y reemplazándola, la estructura económico-privada dentro de la economía pública. Wagner presenta tres razones para esta participación creciente del Estado (Bird, 1971):
Funciones crecientes de administración y seguridad del Estado debido a sustitución de actividad privada por pública. Además, como consecuencia de una mayor complejidad de las comunicaciones y las relaciones legales, que inevitablemente acompañan a la mayor división del trabajo debida a la industrialización, surgen nuevas necesidades de actividades de protección y regulación pública. El crecimiento de la densidad de la población y el desarrollo urbano son fuerzas dirigentes adicionales detrás del aumento del gasto público para mantener la ley, el orden y la regulación económica, así como para asegurar la eficiencia en la economía a pesar de los problemas de la vida urbana.
Considerable expansión relativa de los gastos en cultura y bienestar, especialmente los relacionados con la educación y la redistribución de la renta. En otros términos, estos son bienes superiores o de lujo y tienen una elasticidad renta mayor que la unidad.
Los cambios inevitables en las tecnologías y el volumen cada vez mayor de inversión requerida en muchas actividades crearán un número creciente de monopolios privados que el Estado tendrá que suprimir, o al menos neutralizar sus efectos, por razones de eficiencia económica. En algunos casos -tales como los ferrocarriles- el volumen de inversión será tal que la actividad únicamente puede ser financiada por el Estado.
La ley se sitúa en el contexto del siglo XIX y se refiere a Estados en los que se está produciendo la industrialización, lo que hace que las condiciones previas de Wagner para que se cumpla la ley sean las siguientes (Timm, 1961): i) crecimiento en la renta nacional y el bienestar general e incluso en la renta per cápita, ii) importancia del progreso tecnológico, iii) Estado constitucional y democrático: participación de la población en las decisiones político-financieras.
Wagner era consciente de que su ley implicaba, en algún grado, la suposición de la expansión continuada de las funciones del Estado. Como consecuencia, estableció dos limitaciones: 1) material, pues pensaba que ciertas partes de la economía no deberían ser competencia del Estado (la agricultura o el comercio, por ejemplo) y 2) financiera, en el sentido en que los requerimientos impositivos no podían ser tan altos que supusiesen una carga intolerable para los contribuyentes. Consideraba entonces que hay una proporción del gasto público y la renta nacional que no puede ser permanentemente excedida. Esto confirma la regla de que debe haber alguna clase de equilibrio entre los pagos hechos por los individuos para satisfacer sus diferentes necesidades. En circunstancias extremas, los requerimientos del Estado financiados por impuestos son un gasto en el presupuesto familiar de los ciudadanos privados.
El hecho de que Wagner no le diera a su ley una forma matemática ha contribuido probablemente a su gran simplificación. Numerosos autores se han limitado a contrastar empíricamente la elasticidad renta del gasto público, utilizando un modelo bivariante en el que la variable independiente es alguna de las formas de la renta y la dependiente es alguna forma del gasto público. En muy pocos casos, si acaso hay alguno, se han analizado la validez de las condiciones fijadas por Wagner para el cumplimiento de su hipótesis.
Los primeros contrastes empíricos de la ley se remontan a mediados del siglo XX (Martin y Lewis, 1956)2. Desde 1990 se ha utilizado, en los numerosos artículos sobre la ley, la metodología de raíces unitarias y cointegración en series temporales. Los pioneros fueron los artículos de Henrekson (1990, 1993) y Murthy (1993) . Este tipo de análisis permite una distinción entre las relaciones dinámicas a corto y largo plazo (Henrekson, 1990, 1993; Gemmell, 1993; Hondroyiannis y Papapetreou, 1995; Biswal, Dhawan y Lee, 1999; Burney y Al-Musallam, 1999; Petry et al. 2000; Legrenzi, 2000; Karagianni, Pempetzoglou y Strikou, 2002; Burney, 2002; Chang, 2002; Chang, Liu y Caudill, 2004; Wahab, 2004; Akitoby et al., 2006).
El desarrollo de las técnicas de cointegración utilizando datos de panel ha permitido contrastes de la ley para grupos de países (Lamartina y Zaghini, 2008; Magazzino, 2012a; Magazzino, Giolli y Mele, 2015) y para un país individual (Narayan, Nielsen y Smith, 2008; Susetyo et al., 2017). Finalmente debe considerarse la posibilidad de rupturas estructurales y cambios de régimen en los datos (Priesmeier y Koester, 2012; Richter y Paparas, 2013; Kuckuck, 2014; Cavicchioli y Pistoresi 2016; Keho 2016; Pistoresi, Rinaldi y Salsano, 2017; Afonso y Alves 2017).
En el caso de España, podemos citar cuatro artículos recientes, sin olvidar que el trabajo pionero es Comín (1985) : Jaén-García (2011) utiliza datos de panel para España en el período 1984-2009, y sus resultados muestran que la ley de Wagner no puede rechazarse para el período y los datos considerados. Díaz-Fuentes y Revuelta (2013) consideran el período 1850-2000 y Jaén-García (2017) el período 1901-2011. Ambos utilizan la metodología de raíces unitarias, cointegración y causalidad considerando las rupturas estructurales que se producen en las series. En ningún caso la ley puede ser rechazada para las variables y períodos considerados. Jaén-García (2018) considera como variable proxit al gasto público el empleo de las administraciones públicas. El resultado lleva a rechazar la ley para España en la creencia de que existen otras variables que influyen en el crecimiento del gasto público además del PIB. Los resultados obtenidos en los contrastes en los diferentes países son muy diversos. La lista estándar de factores que pueden explicar la inconsistencia entre los resultados obtenidos por diferentes autores incluye: 1) la calidad y cantidad de los datos, 2) los procedimientos de contraste y el período examinado, 3) el nivel escogido de agregación temporal (puesto que los datos son recopilados en diferentes momentos en el tiempo), 4) la especificación econométrica y 5) la influencia de variables omitidas.
2. UNA BREVE SEMBLANZA DEL GASTO PÚBLICO EN ESPAÑA EN EL PERÍODO 1850-2016
Las ideas sobre la intervención del sector público en la economía y, en consecuencia, la magnitud del gasto público han ido variando a lo largo del tiempo. Para Smith (1979) , el gasto público debería reducirse al mínimo ya que era sinónimo de gasto improductivo, y debía limitarse a las partidas indispensables que acotaban los deberes del soberano: gastos de defensa nacional, gastos para financiar la justicia y el orden interno y gastos para el mantenimiento de las obras e instituciones públicas. Mill (1951) es partidario de la mínima intervención de la autoridad en la economía. Su principal papel es el de la protección contra la fuerza y el fraude. Sidgwick (1883) plantea el conflicto entre eficiencia y equidad, y establece que aunque la no intervención del gobierno es deseable, sus resultados llevan a la desigualdad. Considera que la riqueza produce ansias de poder, lleva al abuso en la utilización de la renta y provoca esclavitud. Pigou (1962) se decanta a favor del intervencionismo. En este sentido, hace hincapié en los fallos del mercado: los desincentivos entre propietarios y arrendatarios de fincas, los efectos externos (iluminación pública, caminos, parques, investigación), perjuicios de la libertad de inversión exterior, no cuidar de las madres embarazadas, monopolios y rendimientos crecientes a escala. Keynes (1936) planteó que los mercados no se pueden ajustar por sí mismos en el corto plazo, sino que es necesaria la intervención de una fuerza exógena al mercado para lograrlo. Su propuesta es que el Estado, a través del gasto público, movería las fuerzas del mercado de modo que propiciaría el aumento del empleo y el ajuste entre oferta y demanda de bienes, así como de ahorro e inversión, pues no existen en el mercado mecanismos que aseguren tal ajuste. Existen circunstancias en las cuales es deseable mantener un déficit fiscal para estimular la actividad económica.
Esta postura, que parte de la teoría de los fallos del mercado, ha tenido su continuidad en la denominada escuela keynesiana. En la actualidad hay un amplio debate entre los economistas en cuanto a si el sector público debería intervenir para controlar las fluctuaciones a corto plazo en la actividad económica, o bien no debería hacerlo. Mientras los economistas clásicos se han opuesto siempre a esa clase de acción pública, la escuela keynesiana invoca políticas fiscales para apoyar la economía durante las recesiones. De hecho, para los economistas clásicos, las fuerzas del mercado tenderán rápidamente a llevar la economía a un equilibrio a largo plazo, a través de ajustes en el mercado de trabajo. Sin embargo, los keynesianos postulan la falibilidad de estos mecanismos autorregulatorios, debido a las rigideces del mercado de trabajo. A este fin, la escuela prescribe políticas fiscales expansivas para evitar largas recesiones3. Los años posteriores a la Segunda Guerra Mundial -con el incesante incremento del sector público y la ausencia de grandes crisis económicas, la superioridad de las economías capitalistas sobre las socialistas y la creciente evidencia de que el socialismo no conduce a la justicia, la libertad ni a la prosperidad-, crearon el caldo de cultivo para que se empezara a producir cierto desencanto por la ineficiencia del sector público al intentar paliar los fallos del mercado, con respecto a la forma de adopción de decisiones colectivas y por la burocracia.
La crisis del petróleo de 1973 provocó un cambio en el paradigma de funcionamiento de la economía, posterior a la Segunda Guerra Mundial, de intervención del Estado. Se pone en cuestión tanto la magnitud de la intervención y la forma de realización de la misma como su eficiencia. En los años posteriores se produce una reestructuración del sector público en la mayoría de los países europeos incluyendo a España con privatizaciones de empresas públicas y una menor intervención del sector público en los mercados. Se considera que un mayor gasto público no es necesariamente la cura para muchos problemas sociales ni contribuye necesariamente a un mayor bienestar. Hay una mayor apreciación de los graves problemas macroeconómicos derivados de los déficits fiscales y las elevadas deudas creadas por los crecientes niveles de gasto público. En la actualidad, las presiones ideológicas o técnicas para reducir el gasto público son, al menos, tan fuertes como las tradicionales para aumentarlo.
No obstante lo dicho en el párrafo anterior y, a modo de resumen, se pueden considerar varios factores institucionales y económicos que ayudan a explicar el crecimiento del gasto público: i) niveles crecientes de prosperidad hacen que la demanda para educación y sanidad crezca con el aumento de la renta4, ii) los procesos políticos dan un sesgo a la conducta presupuestaria en los países de la Unión Europea, lo que hace que los gastos públicos suban durante las recesiones sin caer de nuevo cuando se produce la recuperación. El gasto público como proporción del PIB tiene, por tanto, un efecto trinquete durante los sucesivos ciclos económicos, aunque la tendencia parece haberse roto en los inicios de los noventa, lo que indica que el proceso de convergencia de Maastrich representa una ruptura con la conducta pasada. iii) El precio o coste de suministrar bienes y servicios públicos ha subido más rápido en el sector público en comparación con el privado (la evidencia en este caso es mixta)5. iv) Los factores institucionales en relación con la Constitución nacional o los acuerdos de voto pueden haber permitido a ciertos sectores de la población o grupos de interés organizados persuadir con éxito a los gobiernos para establecer programas de gastos de los que ellos se benefician financiando solo parcialmente su coste a través de la imposición6.
Las ideas vertidas en los párrafos anteriores tienen su reflejo en la hacienda pública española. De acuerdo con Comín (1996) , la hacienda pública española de mediados del siglo XIX solo había de hacerse cargo de gestionar la justicia, la defensa, la policía, la diplomacia y las infraestructuras económicas, en consonancia con las ideas de Smith, aunque la gestión del gobierno de mediados del XIX dejó mucho que desear en todos esos aspectos. Comín (1988) denomina período de la hacienda liberal al que transcurre entre 1833 y 1895 en el que el gasto público es reducido, menos del 10 % del PIB, y se atiende por parte del Estado a la satisfacción de los bienes públicos puros en el sentido de Smith.
Entre 1850 y 1890, España creció a mayor ritmo que otras economías europeas, un 1,7 % anual, pero más lentamente que otras. Si se añade el período de 1840-1850, que fue más expansivo que el inmediatamente posterior, se concluye que estas cuatro décadas fueron favorables al desarrollo económico, aunque con moderación (Bolt and van Zaden, 2014). Aumentaron las distancias, desde el punto de vista del PIB con respecto a Alemania y Gran Bretaña, pero disminuyeron con respecto a Francia. El PIB per cápita era, en 1890, la mitad que el de Gran Bretaña y un 25 % a Francia y Alemania.
Las sucesivas reformas fiscales no consiguieron aumentar la recaudación y, aunque se pusieron en marcha diversos métodos de amortización de deuda, no se pudo equilibrar el presupuesto del Estado. Este desequilibrio no puede atribuirse a la evolución del gasto. Aunque este aumentó ligeramente por encima del PIB, excepto en el primer quinquenio de la década de 1870, fue el servicio de la deuda y los gastos de los ministerios militares y de servicios generales los que acapararon proporciones muy elevadas del gasto total (Pascual y Sudría, 2010; Comín, 1996). Entre 1882 y1895 predominaron los déficits anuales, aunque generalmente de pequeña cuantía, porque la gestión presupuestaria se dirigía a la búsqueda del equilibrio. Sin embargo, los conflictos de 1895-1898 forzaron a los gobernantes a conseguir recursos para hacer frente al enorme incremento del gasto. Las necesidades de guerra obligaron a emitir diversos empréstitos que movilizaron masivamente el ahorro nacional.
El gasto público era inferior al 10 % del PIB. En relación con los niveles de renta y con el presupuesto del Estado, el coste directo de las guerras coloniales alcanzó casi el gasto público ordinario acumulado durante los años de 1895 a 1896 y cerca del 40 % de la renta nacional española de cualquiera de esas anualidades. Al término de las guerras coloniales, el Estado se enfrentaba a una situación de segura insolvencia. Sin embargo, las reformas de Villaverde consiguieron una rápida liquidación de los efectos de los conflictos. En todo caso, en 1900 el nivel de endeudamiento era trece veces superior a los ingresos del Estado y en 1913 era casi siete veces los recursos públicos del ejercicio. La magnitud del endeudamiento a lo largo del siglo XIX aparece como una de las causas mayores de la debilidad del crecimiento y del retraso en la modernización de España (Maluquer de Motes, 2010). Hasta 1920, gasto, ingreso y PIB permanecen bastante estables en valores cercanos al 10 % del PIB y a partir de entonces se produce un ligero crecimiento. Entre 1895 y 1902, el gasto crece relativamente con respecto al período anterior y se produce una bajada entre 1902 y 1912. Sin embargo, con el comienzo de la Primera Guerra Mundial, el gasto público crece por encima del 10% del PIB. A partir de aquí se produce una fase alcista que durará hasta 1920 en la que España conoció una coyuntura excepcional que alentó un notable crecimiento económico seguido de una fase de estancamiento en 1921-1923. Entre 1924 y 1930 se produce un notable crecimiento que finalizó con la moderada crisis de 1931-1934 y se observó una recuperación económica en 1934 y 1935. En el primer período, el PIB per cápita apenas creció al 0,6 % anual. A diferencia de ello, entre 1924 y 1930, el aumento en el PIB per cápita fue del 2,5 % anual. En 1931 cayó el PIB a precios corrientes, aunque ya en 1934 se había recuperado el nivel de 1930. El gasto creció moderadamente entre 1913 y 1935 (del 10,5 % al 12,4% del PIB) y mostró una hacienda en lenta transición hacia el Estado del bienestar. El presupuesto de gastos cambió ligeramente su estructura, con lo que cayó el gasto en defensa y deuda pública y aumentó el gasto en servicios económicos. Los gastos en educación, pensiones y vivienda apenas crecieron. De acuerdo con Comín (1988, 1996, 2010) es un periodo transicional en el que se proyectan mayores gastos en servicios económicos, bienes preferentes y seguros sociales que no se llevan a cabo debido a la penuria de la hacienda pública. En 1909 estalló la guerra con Marruecos, lo que aumentó el gasto en defensa, que perduró hasta 1925, y precipitó un aumento del déficit. El sector público incrementó su grado de intervención en la economía durante la dictadura de Primo de Rivera, tendencia que se mantuvo y que varió el tipo de intervención con la llegada de la Segunda República (García Santos y Martín, 1990; Díaz-Fuentes y Revuelta, 2013).
La Guerra Civil y la autarquía marcaron el periodo de 1936 a 1959 (Díaz-Fuentes y Revuelta, 2013). Al terminar la guerra, todos los parámetros con relación al PIB habían caído. Disminuyó la producción agraria en un 20 % y la industrial en un 30 %. El país carecía de reservas de oro y no tenía divisas. Las infraestructuras, en particular las ferroviarias, sufrieron grandes pérdidas. El nuevo Estado tuvo como uno de sus rasgos sobresalientes el intervencionismo y el dirigismo estatal. Se impuso una fuerte autoridad que ordenaba y regulaba la actividad económica. Al acabar la guerra, la hacienda española presentaba los problemas derivados de las deudas de guerra y de las necesidades de reconstrucción. Por ello, una reforma tributaria que permitiera un sustancial incremento de los ingresos resultaba imprescindible e inaplazable. El intento de reforma del ministro Larraz resultó decepcionante, con lo que se produjo una situación crítica desde el punto de vista del ingreso, que derivó en una cuidadosa organización de los gastos del Estado. En 1940 el gasto público aumenta ligeramente con respecto a 1935, pero oscila hacia arriba y hacia abajo en los años posteriores marcados por los acontecimientos de la Segunda Guerra Mundial, en la que España se mantiene neutral. Al acabar la contienda, se produce una fuerte bajada en el gasto público debido a la disminución de los gastos en defensa, y no se vuelve a alcanzar el gasto de 1935 hasta el año 1958 (Barciela López, 2010).
Para Prados (2003) existe una continuidad en el crecimiento a largo plazo del PIB en el periodo 1850-1958 con un descenso del nivel correspondiente a la Guerra Civil. La tasa anual de crecimiento es del 2,4 %, aunque la Guerra Civil provoca una fuerte caída que se puede cifrar en el 8 % de dicha tasa de crecimiento. La evolución del PIB marca un máximo en 1935, valor que no se vuelve a alcanzar hasta 1952. En términos per cápita, el PIB evoluciona en el mismo sentido, pues se produce un incremento en 1940 en relación con 1935 que se mantiene en los años de postguerra española y la Segunda Guerra Mundial, pero una vez pasada dicha situación de guerra se cae a valores inferiores a los de 1935 y no se vuelve a recuperar este valor hasta 1962.
Entre 1960 y 1975 transcurre el período final de la dictadura franquista. En 1959 se pone en marcha el Plan de Estabilización que empuja el crecimiento económico. El PIB aumentó, en términos reales, a una tasa anual superior al 7 % a lo largo de quince años seguidos. Este crecimiento fue posible gracias al retorno de España a la escena económica internacional, tras los dos decenios de aislamiento autárquico, que le permitió aprovechar la expansión en los países desarrollados que tampoco tenía precedentes. La economía española tenía una gran variedad de regulaciones mientras que la intervención hacendística era muy limitada. El gasto público, en términos reales, era menor que el 25 % del PIB. Se mantiene por debajo del 20 % del PIB en la primera parte (19,5 % en 1965), a diferencia del resto de países de la futura Unión Europea 15 (33,1 %) y de la OCDE (26,9 %), y lo supera ligeramente en la parte final (24,1 % en 1975), aunque en ese momento en el área Euro era del 40,9 % y en la OCDE del 34,4 %. A pesar del lento crecimiento, hay cambios notables en la composición del gasto en relación con etapas anteriores, además se recuperaron los niveles previos a la Guerra Civil. Disminuyen los gastos en servicios generales, defensa e intereses de la deuda y se produce una mayor atención a los servicios de tipo económico y a las funciones de carácter social (Serrano y Pardos, 2010).
La intervención del Estado en la economía se llevaba a cabo a través de la regulación en la forma de leyes y estatutos. En los años sesenta del siglo pasado, la industrialización ayudó al crecimiento del gasto público. En la línea de la tradición wagneriana, el desarrollo económico fue de la mano con un aumento en la población, educación, urbanización, salud y redistribución del ingreso (Tamames, 1993; González, 1998; García Delgado, 2015). Ya con la instauración de la democracia en 1976 se produjo una rápida expansión del gasto público en España. Dicho gasto aumentó desde el 23,19 % del PIB al 42,5 %, en línea con los países de la OCDE, cuyo promedio de gasto representaba el 47 % del PIB. Entre 1976 y 1982 se produce un intenso crecimiento en el gasto público con una tasa anual acumulativa, en términos nominales, del 25,5 % que se puede atribuir a tres factores (Alcaide, 1988): la transición política, la manifestación de las consecuencias más graves de la crisis económica y la existencia de los gobiernos débiles de Unión de Centro Democrático (UCD) y la fuerte oposición del Partido Socialista Obrero Español (PSOE). A partir de 1983, aunque continúa el crecimiento con una tasa acumulativa anual, en términos nominales, del 15,3 %, es menor debido a diversos factores, entre los que destaca una menor virulencia de la crisis económica y, sobre todo, la entrada en una fase de recuperación de la economía desde mediados de 1985. En este momento hay una mayoría absoluta del partido gobernante y un régimen democrático consolidado.
En 1986 se produjo la entrada de España en la Comunidad Económica Europea. En 1993, el gasto público supone un 49,66 % del PIB. Para Valle (1996) no existe ninguna experiencia cercana de países en los que, en tan solo veinte años, la proporción del gasto público total, no financiero, se haya duplicado prácticamente. Ello le lleva a afirmar que en este período de tiempo se ha seguido con absoluta fidelidad la ley de Wagner. Al mismo tiempo, se ha ido consolidando el estado de las autonomías. Así, la gestión de ese enorme crecimiento del gasto ha ido recayendo en unas administraciones públicas que se están poniendo en marcha en esos momentos, con lo que unen a su falta de experiencia el trasvase de competencias. El crecimiento del gasto fue determinado por la política del nuevo gobierno del PSOE que se puso en marcha por un Estado del bienestar en España. La universalización de la sanidad pública y el aumento del número de pensionistas a través de las pensiones no contributivas, así como el incremento de la cuantía de las pensiones, contribuyeron a un mayor gasto público. De la misma forma, la educación se hizo obligatoria hasta los dieciséis años y se realizaron acuerdos con el sistema privado de educación que recibió subvenciones del Estado para garantizar la gratuidad de la educación en el tramo de edad entre los seis y los dieciséis años. Por último, se produjo la consolidación de las comunidades autónomas que recibían cada vez un mayor número de transferencias del Estado central con las consiguientes necesidades de gasto. Todo ello provocó un fuerte aumento en el gasto con deterioro del equilibrio presupuestario. En 1993 el déficit público alcanza su valor más elevado en el período democrático en relación con el PIB (5,9 %).
Entre 1994 y 1998 se produjo un drástico cambio en el sector público español. Las razones básicas para este cambio se encuentran en la necesidad de cumplir en su totalidad las condiciones del tratado de Maastrich así, como el pacto de estabilidad y crecimiento (PEC), en conjunción con que este período coincide con el principio de la fase ascendente del ciclo económico en 1996. Los elevados déficits presupuestarios (7,3 % del PIB en 1994) caen al 2,6 % en 1998, por lo que cumplen de forma estricta las condiciones del PEC (3 %) con respecto a los déficits presupuestarios. La consolidación de la recuperación económica a lo largo de 1994, el aumento del empleo, la corrección del desequilibrio exterior, la moderación salarial y los avances conseguidos en la reducción de la inflación y del déficit público fueron los resultados más significativos de la política gubernamental.
La burbuja inmobiliaria dio lugar a un elevado crecimiento, de forma que en 2001 se logra un presupuesto equilibrado, aunque el gasto público supone el 40 % del PIB, lo que indica una subida del 4 % con respecto al promedio del periodo 1997-2001. El período de la burbuja posibilitó un fuerte crecimiento del empleo unido a un gran aumento de la venta de viviendas, lo que dio lugar a un aumento de la recaudación fiscal tanto directa -vía impuesto sobre la renta de las personas físicas (IRPF) por el incremento del empleo en el sector de la construcción y en otros sectores- como indirecta debido a la recaudación por el impuesto sobre el valor añadido (IVA) de la venta de vivienda nueva y el impuesto de transmisiones patrimoniales en la venta de vivienda usada. Por otra parte, aumentó la recaudación en impuestos locales derivados de la construcción de viviendas. En 2008 la economía española, arrastrada por la caída en las economías estadounidenses y europeas y sus propios problemas internos, entró en una severa recesión de la que recientemente empezó a emerger con algún crecimiento positivo del PIB (en 2014 1,4 % y 3,3 % en 2016) y con elevados déficits presupuestarios (5,97 % en 2014, 5,28 % en 2015 y 4,51 % en 2016). Incluso, aunque el gasto público actual en España ha crecido en relación con períodos anteriores, hay una diferencia con respecto al resto de países europeos de la OCDE. En los años finales del siglo XIX había cierta convergencia en el gasto público entre España, 10 % del PIB y los países europeos, Francia 10 % y Reino Unido 10 %. En los años posteriores se produce un distanciamiento, de forma que en 1920 la ratio era del 8 % para España, del 32 % para Francia y del 26 % para el Reino Unido (Comín, 1988). La distancia es muy elevada en los años siguientes, en 1955 el gasto público español era inferior al 10 % del PIB, mientras en Francia era del 30 % y del 23 % en Alemania. En 1960, la ratio en relación con el PIB era del 19,8 % mientras que en los países europeos era del 29,5 %. En el total de la OCDE el porcentaje era del 26,6 %. En menos de treinta años, las ratios eran UE27, 46,1 %; UE15, 50,9 % y OCDE 41,1 %. En 2016 las ratios eran UE27, 48,1 %; UE15, 49,2 %; OCDE 41,2 % y España 43,6 %.
Para Comín y Díaz (2005) la experiencia española parece confirmar el cumplimiento de la ley de Wagner, mientras que el efecto desplazamiento de Peacock y Wiseman (1961, 1967) cuenta con menos evidencia empírica en el caso español durante las dos guerras mundiales y la Guerra Civil, pues si bien está claro que los acontecimientos bélicos y los trastornos sociales ocasionan fluctuaciones en la relación entre el gasto del Estado y la renta nacional, las alteraciones en esa relación no tienen la forma de escalera predicha por aquella teoría. Según su criterio, el efecto desplazamiento sí que actuó en España de forma destacada en la etapa de transición a la democracia, tanto por la crisis económica como por los importantes cambios políticos y sociales que estaba experimentando el país y que dieron lugar a la consolidación del Estado del bienestar.
3. CONTRASTACIÓN EMPÍRICA DE LA LEY UTILIZANDO RAÍCES UNITARIAS Y COINTEGRACIÓN
En este apartado se analiza el cumplimiento de la ley de Wagner para la economía española utilizando una base de datos desde 1850 a 2016 para gasto público del Estado y producto interior bruto. Utilizamos metodología de raíces unitarias y cointegración con rupturas estructurales y análisis wavelet. Las series utilizadas en este apartado son: gasto público estatal (GP), producto interior bruto (PIB) y producto interior bruto per cápita (PIBpc) para el período 1850-2016. Los datos de gasto público se han tomado de Comín y Díaz (2005) hasta 2001 y de la Intervención General de la Administración del Estado (IGAE) y el Instituto Nacional de Estadística (INE) desde 2002 a 2016. Los datos del PIB son de Carreras, Prados y Rosés (2005) hasta 2000 y del INE entre 2001 y 2016. Tomamos todas las variables en logaritmos7.
Para el análisis empírico utilizamos dos de las cinco formulaciones de la ley de Wagner8. La formulación de Mann (1980) :
(1)
y la de Musgrave (1970) :
(2)
La primera relaciona la ratio GP/PIB con el PIB y la segunda la ratio GP/PIB con el PIB per cápita. La formulación se realiza en logaritmos, de forma que el coeficiente del PIB en sus dos formulaciones es la elasticidad renta. Se espera que dicha elasticidad sea positiva para que la ley de Wagner no sea rechazada9. La elección de estas dos formulaciones viene determinada por la intención de comparar los resultados obtenidos utilizando la metodología habitual de raíces unitarias y cointegración, en contraposición a la metodología wavelet que nos permite conocer el orden de precedencia de las variables y la existencia de cambios o rupturas estructurales en la relación entre las series, pero no cuantificar la magnitud de la relación. En ambas formulaciones el coeficiente de la variable independiente debe ser positivo sin especificarse su magnitud, lo que concuerda con la metodología wavelet. Se supone que los gastos públicos no alcanzan su nivel deseado en el corto plazo. Solo en el largo plazo alcanzan su nivel deseado o nivel de equilibrio. Suponiendo la relación en el estado estacionario entre las variables para una de las ecuaciones anteriores, tendremos10:
(3)
Si el ajuste al estado estacionario es gradual, el nivel de Y responderá a cambios transitorios en X, y Y se moverá gradualmente hacia su estado estacionario o nivel de equilibrio. Para tener en cuenta este movimiento gradual se especifica un modelo de retardo distribuido autorregresivo en la siguiente forma:
(4)Para reflejar el estado estacionario, la ecuación anterior puede presentarse como un modelo de corrección de error, tal como se muestra en la ecuación [5].
(5)
Lo anterior puede interpretarse en el sentido de que ν0∆LnXt es el impacto a corto plazo de X en Y, y ν0 es la elasticidad a corto plazo de Y con relación a X. El término de corrección de error LnYt-1-ψLnXt-1 reúne las desviaciones a corto plazo donde ψ es la elasticidad a largo plazo de Y con respecto a X y ρ es la tasa a la cual Y ajusta los desequilibrios pasados. La derivación anterior deja clara la suposición subyacente de que hay una relación de elasticidad constante entre Y y X, mientras que las desviaciones transaccionales son constantes.
Comenzamos nuestro análisis de ambos modelos usando raíces unitarias y cointegración para contrastar la existencia de la relación a largo plazo entre ambas variables en la línea de la ley de Wagner. La longitud de las series y los cambios políticos y económicos que se han producido en España entre finales del siglo XIX y principios del siglo XXI nos inducen a pensar que deben existir cambios de régimen o rupturas estructurales en las dos series. Por esta razón, permitimos rupturas estructurales en las series tanto en los contrastes de raíces unitarias como en los de cointegración (Priesmeier y Koester, 2012; Richter y Paparas, 2013; Kuckuck, 2014). Estas rupturas estructurales pueden derivar de cambios en la economía o en los diferentes factores que afectan a las series utilizadas. En esta situación, si no se toman en consideración dichos cambios estructurales cuando se investiga la existencia de una relación a largo plazo, podemos encontrarnos con que dicha relación no se detecta cuando en realidad existe.
En la tabla 1 consideramos los estadísticos descriptivos, los coeficientes de correlación y las gráficas de las series. El gráfico 1 indica que las series son crecientes a lo largo del tiempo, aunque la primera muestra muchos picos y un fuerte crecimiento a partir de 1980. En la tabla 2 observamos que la variable dependiente está fuertemente correlacionada con las independientes, lo que corroboran las dos últimas gráficas.
Tabla 1 Estadísticos de las series
| LnGP/PIB | LnPIB | LnPIBpc | |
|---|---|---|---|
| Media | 2,56 | 14,77 | 8,51 |
| Mediana | 2,47 | 12,80 | 8,14 |
| Máximo | 3,74 | 21,31 | 10,04 |
| Mínimo | 2,09 | 10,86 | 7,42 |
| Desviación estándar | 0,36 | 3,67 | 0,83 |
| Sesgo | 0,95 | 0,63 | 0,63 |
| Curtosis | 2,99 | 1,81 | 1,87 |
| Jarque-Bera | 24,39 | 19,83 | 18,86 |
Fuente: elaboración propia.
Tabla 2 Correlación entre las series
| LnGP/PIB | LnPIB | LnPIBpc | |
|---|---|---|---|
| LnGP/PIB | 1 | 0,82 | 0,81 |
| LnPIB | 0,82 | 1 | 0,99 |
| LnPIBpc | 0,81 | 0,99 | 1 |
Fuente: elaboración propia.
En la tabla 3 se tienen los diferentes contrastes de raíces unitarias de las series del modelo sin considerar rupturas estructurales. Se observa que los contrastes confirman la existencia de una raíz unitaria I (1) en las tres variables consideradas.
De acuerdo con Perron, los contrastes estándar de raíces unitarias tienden a identificar erróneamente procesos estacionarios en tendencia como estacionarios en diferencia y pueden tener un poder bajo, incluso asintóticamente, si se ignoran los cambios de régimen. Dado que en el largo período estudiado se producen numerosos cambios tanto políticos como económicos que pueden haber alterado el desarrollo de las variables estudiadas, tenemos que suponer que existen puntos de ruptura y consideramos los contrastes adecuados para detectarlos, así como para analizar si existen raíces unitarias en esos puntos. Consideramos los contrastes usuales Perron (P), Zivot-Andrews (ZA), Lumsdiane-Papell y el ADF con rupturas estructurales (tabla 4). Los dos primeros y el cuarto detectan, de forma endógena, un punto de ruptura mientras el tercero detecta dos puntos de ruptura.
Tabla 3 Contrastes de raíces unitarias de las series11
| DF | DFGLS | PP | KPSS | |
|---|---|---|---|---|
| LnGP/PIB | −0,52 | 0,62 | −0,69 | 1,13 |
| LnPIB | −1,63 | −1,08 | −1,57 | 0,39 |
| LnPIBpc | −1,40 | −1,08 | −1,32 | 0,32 |
| ∆LnGP/PIB | −8,41 | −3,14 | −15,59 | 0,13 |
| ∆LnPIB | −2,90 | −2,60 | −8,07 | 0,73 |
| ∆LnPIBpc | −10,01 | −9,96 | −10,01 | 0,28 |
Fuente: elaboración propia.
Tabla 4 Contrastes de raíces unitarias con rupturas estructurales12
| P (VC) | ZA (VC) | LP (VC) | ADF raíces unitarias con rupturas estructurales (VC) | |
|---|---|---|---|---|
| LnGP/PIB | −3,75 (−5,23) 1977 | −4,10 (−4,93) 1978 | −4,02 (−6,16) 1945 1977 | −4,18 (−4,44) 1977 |
| LnPIB | −2,47 (−5,08) 1945 | −2,54 (−5,59) 1946 | −4,58 (−6,16) 1945 1.970 | −3,37 (−4,85) 1945 |
| LnPIBpc | −4,06 (−5,08) 1960 | −4,05 (−5,59) 1961 | −5,31 (−6,16) 1929 1960 | −4,37 (−4,85) 1960 |
| ΔLnGP/PIB | −17,91 (−5,23) | −8,90 (−4,93) | −7,27 (−6,16) | −16,67 (−4,44) |
| ΔLnPIB | −6,19 (−5,23) | −6,42 (−4,93) | −6,48 (−6,16) | −9,14 (−4,44) |
| ΔLnPIBpc | −11,63 (−5,23) | −10,54 (−4,93) | −7,20 (−6,16) | −11,63 (−4,44) |
Fuente: elaboración propia.
Los valores obtenidos utilizando los diferentes contrastes confirman que las tres series son I (1).
Nuestro siguiente paso es analizar la existencia de cointegración entre ambas series teniendo en cuenta la posible existencia de rupturas estructurales en los datos y en las ecuaciones. Para ello, implementamos diferentes contrastes de cointegración. Como punto de partida analizamos la existencia de cointegración sin tener en cuenta las rupturas estructurales. En este caso aplicamos los contrastes usuales para una única ecuación de Engle-Granger (EG), Phillips-Outlaris (PO), así como el contraste de estabilidad de Hansen (H) y el contraste de variables añadidas de Park (P)13.Además, realizamos el contraste de Johansen-Juselius (JJ) que considera la posibilidad de múltiples ecuaciones de cointegración. En los dos primeros la hipótesis nula es la no existencia de cointegración entre las variables, mientras que en la tercera y la cuarta es la existencia de cointegración. Los resultados obtenidos se muestran en la tabla 5.
Tabla 5 Contrastes de cointegración (1)
| Constante estadístico τ | Constante estadístico z | Tendencia lineal estadístico τ | Tendencia lineal estadístico z | ||
|---|---|---|---|---|---|
| Mod1 | EG | −2,98 (0,11) | −24,26 (0,01) | −3,07 (0,24) | −26,00 (0,04) |
| PO | −3,28 (0,06) | −24,38 (0,01) | −3,09 (0,24) | −26,00 (0,04) | |
| Mod2 | EG | −3,15 (0,08) | −26,72 (0,01) | −3,28 (0,18) | −28,14 (0,03) |
| PO | −3,37 (0,05) | −25,18 (0,01) | −3,44 (0,12) | −26,15 (0,04) |
Fuente: Elaboración propia.
En el contraste de Hansen (H) se obtiene un valor crítico del estadístico LC de 0,31 (0,13) y en el de Park (P) un valor de χ2 de 1,67 (0,48) para el primer modelo y 0,37 (0,08) y 4,56 (0,10) para el segundo, con lo que los contrastes EG y OP rechazan la existencia de cointegración entre las dos variables mientras que los contrastes H y P, asimismo, aceptan dicha cointegración.
En el contraste JJ, atendiendo a los criterios AIC y SC, se han considerado dos y tres retardos en el VAR para el primer y segundo modelo respectivamente. Los resultados se tienen en la tabla 6.
Tabla 6 Contraste de cointegración Johansen-Juselius
| Traza | Valor propio máximo | |
|---|---|---|
| Modelo1 r=0 | 16,17 (15,48) | 15,16 (14,26) |
| r≤1 | 1,01 (3,84) | 2,07 (3,84) |
| Modelo 2 r=0 | 29,51 (20,20) | 23,24 (15,89) |
| r≤1 | 6,27 (9,16) | 6,27 (9,16) |
Fuente: elaboración propia.
Por su parte, los contrastes JJ muestran que existe una única relación de cointegración entre las dos variables tanto en el primer modelo como en el segundo. Se realiza un segundo análisis considerando los puntos de ruptura en el cual se utilizan los contrastes de Gregory-Hansen (GH), donde el contraste detecta endógenamente un punto de ruptura, y el de Johansen-Mosconi y Nielsen (JMN), en el que se pueden considerar uno o dos puntos de ruptura en las variables en niveles14. Para calcular los puntos de ruptura en el contraste JMN hemos utilizado el procedimiento de Bai-Perron (tablas 7 y 8).
Tabla 7 Contraste secuencial de Bai-Perron
| Contraste de ruptura | Estadístico F | Estadístico F escalado | Valor crítico | Puntos de ruptura | |
|---|---|---|---|---|---|
| Modelo 1 | 0 vs. 1 * | 40,52 | 81,04 | 11,47 | 1982 |
| 1 vs. 2 * | 17,16 | 34,33 | 12,95 | 1950 | |
| Modelo 2 | 0 vs. 1 * | 47,72 | 95,45 | 11,47 | 1982 |
| 1 vs. 2 * | 8,47 | 16,93 | 12,95 | 1950 |
Fuente: elaboración propia.
Tabla 8 Contrastes de cointegración con rupturas estructurales
| Modelo 1 | Puntos de ruptura | Modelo 2 | Puntos de ruptura | |
|---|---|---|---|---|
| GH | −3,62 (−4,61) | 1944 | −3,40 (−4,61) | 1944 |
| JMN115 | 28,40 (26,34) | 1950 | 26,99 (26,34) | 1950 |
| 9,33(10,44) | 8,89 (10,44) | |||
| JMN2 | 25,64 (37,14) | 1950 | 25,39 (37,14) | 1950 |
| 11,13 (18,81) | 6,94 (18,81) | |||
| JMN1 | 44,03 (34,18) | 1982 | 28,86 (34,18) | 1982 |
| 5,95 (17,22) | 8,94 (17,22) | |||
| JMN2 | 43,41 (25,55) | 1982 | 18,36 (25,55) | 1982 |
| 11,89 (12,30) | 3,26(12,30) | |||
| JMN1 | 38,19 (44,78) | 1950 1982 | 25,95 (44,78) | 1950 1982 |
| 14,18 (23,00) | 7,98 (23,00) | |||
| JMN2 | 21,76 (31,40) | 1950 1982 | 23,29 (31,40) | 1950 1982 |
| 5,97 (16) | 4,91 (16,00) |
Fuente: elaboración propia.
Para el modelo 1 se obtiene cointegración y se consideran los años 195016 y 198217 como puntos de ruptura. Para el modelo 2 se tiene cointegración para 1950. Teniendo en cuenta la existencia de cointegración, podemos formular los modelos de corrección de error correspondientes (tabla 9).
Tabla 9 Modelo de corrección de error
| Variables independientes | |||||||
|---|---|---|---|---|---|---|---|
| Cointegración−1 | ΔLogGP/PIB−1 | ΔLog PIB−1 | ΔLogPIBpc−1 | Puntos de ruptura | R2 | Estadístico F | |
| Modelo 1 | −0,21(−3,67) | −0,24 (−2,76) | −0,21 (−1,48) | −0,07 (−2,17) | 0,11 | 7,15 | |
| −0,00 (−1,50) | −0,35 (−3,82) | −0,19 (−1,86) | −0,05 (−0,97) | 0,09 | 4,03 | ||
| Modelo 2 | −0,07 (−2,38) | −0,28 (−3,19) | −0,17 (−0,77) | −0,04 (−1,24) | 0,11 | 7,13 |
Fuente: elaboración propia.
Los resultados indican que existe causalidad del PIB a ExpPIB y de PIBpc a ExpPIB cuando tenemos ruptura en 1950, pero no en 1982. Para calcular las relaciones de cointegración utilizamos fully modified least squares (FMOLS) (tabla 10).
Tabla 10 Ecuaciones de cointegración de los modelos 1 y 2
| C | LnPIB | LnPIBpc | D1950 | D1982 | R2 | |
|---|---|---|---|---|---|---|
| Modelo 1 | 0,52 (2,76) | 0,15 (9,56) | −0,56 (−4,73) | 0,77 | ||
| 1,93 (12,45) | 0,03 (2,95) | 0,51 (4,79) | 0,78 | |||
| Modelo 2 | −1,96 (−3,47) | 0,55 (7,64) | −0,36 (−2,91) | 0,71 |
Fuente: elaboración propia.
Los contrastes de Wald de los coeficientes de las variables independientes indican que estos son distintos de cero18.
Los resultados obtenidos son bastante informativos. En ambos casos los coeficientes de las variables independientes son positivos y significativos, lo que indica el no rechazo de la ley de Wagner en ambos modelos. Lo mismo ocurre en los puntos de ruptura. Para 1950 el valor obtenido es negativo, lo que indicaría que a partir de ese punto disminuye la deriva en ambas ecuaciones. Al contrario, ocurre en 1982 en el primer modelo en el que la deriva aumenta. No obstante, el coeficiente en 1982 para el modelo 1 es insignificante, con lo que podemos considerar que el coeficiente es cero y no podríamos confirmar la ley de Wagner en ese caso. En consecuencia, al combinar los resultados podríamos considerar que no se puede rechazar la ley de Wagner para España con el modelo 1 y ruptura en 1950, pero sí para el resto de las suposiciones.
4. METODOLOGÍA WAVELET19
El análisis wavelet surge como una alternativa al análisis de Fourier. Con el análisis de Fourier se pueden estudiar series temporales en el dominio de la frecuencia. Sin embargo, bajo la transformada de Fourier, la información temporal se pierde, lo que dificulta distinguir relaciones transitorias o identificar cambios estructurales. Por tanto, la técnica es únicamente apropiada para series temporales estacionarias. Por su parte, el análisis wavelet realiza la estimación de las características espectrales de una serie temporal como una función del tiempo, revelando cómo sus diferentes componentes periódicas cambian a lo largo del tiempo. Además, el análisis wavelet permite la identificación de posibles rupturas en cada periodo de tiempo y frecuencia.
La metodología wavelet parte de una función madre ψ que es una función cuyo cuadrado es integrable y cumple una condición técnica denominada condición de admisibilidad. En la mayoría de las aplicaciones, la función wavelet debe ser una función bien localizada, tanto en el dominio del tiempo como en el dominio de frecuencia, en cuyo caso la condición de admisibilidad se reduce a requerir que ψ tenga media cero, es decir, ∫ ∞ ∞ ψ(t)dt = 0. Esto significa que la función ψ tiene una ondulación hacia arriba y abajo en el eje t, es decir, se comporta como una ola. Esto junto con la propiedad de caída paulatina justifica la elección del término wavelet para designar a ψ.
Empezando con una wavelet madre ψ, una familia ψτ,s de hijas wavelet puede ser obtenida tomando un factor de escalonamiento y trasladando ψ:
(6)
Donde s, τ ЄR s≠0, es un factor de escala o dilatación que controla la anchura de la ola (el factor
s es introducido para garantizar la energía unidad ║ψτ,s║=1) y τ es el parámetro de traslación que controla la localización de la wavelet en el tiempo. Al aumentar s se amplía la wavelet en una función wavelet larga para medir ciclos de largo plazo (frecuencia baja), mientras que al disminuir s la comprime para medir ciclos de corto recorrido (alta frecuencia). Por su parte, la traslación significa simplemente cambiar su posición en el tiempo.
Dada una serie temporal x(t), su transformada wavelet continua (CWT) con respecto a la wavelet ψ, que es una función de dos variables Wx (τ,s):
(7)
Donde la barra superior denota la conjugada compleja. La transformada se considera compleja porque ψ se supone que es compleja. La transformada wavelet proyecta la variable en el dominio tiempo-escala. Se dice que el análisis wavelet se realiza en el dominio tiempo-frecuencia porque hay una relación biunívoca entre escalas y frecuencias, y ambos términos pueden ser usados en forma intercambiable.
En analogía con la terminología utilizada en el caso de Fourier, el espectro de energía wavelet, a veces llamado escalograma o periodograma, wavelet se define como:
(8)
Esto da una medida de la distribución de la varianza de la serie temporal en el plano tiempo/frecuencia. A diferencia del clásico espectro de energía basado en la transformada de Fourier, (WPS)x(τ,s), indica cómo la concentración de la serie temporal x(t) se distribuye en el dominio de frecuencias así como en el dominio temporal. Si se requiere información cuantitativa acerca de las interacciones de fase entre dos series temporales, la mejor elección son las wavelets continuas y complejas. Cuando escogemos una wavelet compleja, la transformada wavelet es también compleja. En este caso, la transformada puede ser separada en su parte real ℜ(Wx) y su parte imaginaria ℑ(Wx) o en su amplitud |Wx (τ,s)| y fase Φx (τ,s) con lo que:
(9)
El ángulo de fase Φx (τ,s) del número complejo Wx (τ,s) puede obtenerse de la fórmula [10].
(10)
Así, se usa la información de los signos del denominador y del numerador para determinar el cuadrante al que el ángulo pertenece. Para funciones de valor real, la parte imaginaria es cero y la fase no está definida. Por tanto, para separar la información de fase y amplitud de una serie temporal es necesario utilizar wavelets complejas. En tales casos, es conveniente escoger ψ(t) para que sea progresiva o analítica, es decir, tal que ψ̂ = 0 para f < 0. De hecho, cuando es analítica y x(t) es real, es posible reconstruir x(t) considerando solo valores positivos del parámetro escalar s. Las wavelets analíticas son ideales para el análisis de señales oscilatorias puesto que la transformada wavelet analítica continua provee un estimador de la amplitud instantánea y de las señales instantáneas en la vecindad de cada localización tiempo/escala (τ,s).
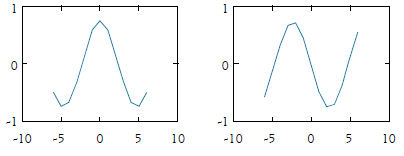
Hay varios tipos de funciónes wavelets disponibles con diferentes características tales como Morlet, Mexican hat, Haar y Daubichies. Puesto que los coeficientes de Wx (contienen una combinación de información de x and ψ(t), seleccionar la wavelet apropiada es una decisión crucial y el propósito de su aplicación debe ser tenido en cuenta. Para las aplicaciones económicas es usual utilizar la wavelet Morlet que tiene la propiedad de que su concentración tiempo-frecuencia es óptima. La wavelet Morlet se define como
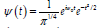donde el primer factor es el factor de normalización que asegura que la wavelet tenga energía unitaria, el segundo es una senoide compleja y el tercero es la función de densidad normal con media cero y desviación típica 1. Los dos gráficos adjuntos (gráfico 2) corresponden a la parte real e imaginaria de una wavelet Morlet.
Es usual escoger el parámetro w 0 = 6 de manera que la wavelet puede considerarse una función de la frecuencia angular w 0 = 6. Se usa la frecuencia f(s) = w 0 /2πs = 6/2πs ≈ 1/s. Por tanto, para esta elección del parámetro la conversión de escalas wavelet (s) a frecuencias es casi inmediata.
El concepto de transformada wavelet cruzada, coherencia wavelet y diferencia de fase son generalizaciones naturales de los instrumentos de análisis wavelet que nos permiten tratar con las dependencias tiempo-frecuencia entre dos series temporales. La transformada wavelet cruzada de dos series x(t) y y(t) se define como:
(11)
Donde W x y W y son las transformadas wavelet de x e y respectivamente. Se define la energía wavelet cruzada como |W xy (τ,s)|. La energía wavelet cruzada describe la covarianza local entre dos series en cada momento del tiempo y frecuencia. Por tanto, la energía wavelet cruzada nos da una indicación cuantificada de la similitud de energía entre dos series temporales.
En analogía con el concepto de coherencia utilizado en el análisis de Fourier, dadas dos series temporales x(t) y y(t) se define su coherencia wavelet como:
(12)
Donde S denota un operador de alisado en tiempo y frecuencia. Varía desde 0 (no hay coherencia) a 1 (coherencia fuerte). Esta cantidad puede interpretarse como el coeficiente de correlación local en el espacio tiempo-frecuencia. Cuando se compara con la energía wavelet cruzada, la coherencia wavelet tiene la ventaja de estar normalizada por el espectro de energía de las dos series temporales.
Como se ha visto anteriormente, una de las principales ventajas de utilizar una wavelet compleja es que podemos calcular la fase de la transformada wavelet de cada serie y así obtener información acerca de los posibles retrasos de las oscilaciones de las dos series como función del tiempo y de la escala/frecuencia. De esta manera, se calcula la diferencia de fase. La diferencia de fase se puede calcular a partir de la transformada wavelet cruzada
(13)
Y la información sobre los signos de cada parte determina completamente el valor de φxy є[- π, π]. La diferencia de fase suministra información acerca de si las variables están liderando o están retardadas en el tiempo y la frecuencia especificados. Cuando φxy € (-π/2, π/2) x y y se mueven en fase (la correlación es positiva) porque Φ x y Φ y tienen casi el mismo valor con una pequeña diferencia de fase. En particular, una diferencia de fase de 0 (es decir φ xy = 0 con lo que Φ x = Φ y ) indica que las series se mueven exactamente juntas en la frecuencia especificada y son completa y positivamente correlacionadas. Si φ xy є (0, π /2), las series se mueven en fase, pero la serie x lidera o precede21 a y porque Φ x es ligeramente mayor que Φ y y la fase de x está liderando; si φxy є (- π/2,0) entonces y precede o lidera a x. Por otro lado, cuando φ xy € (π/2, π) o φ xy € (-π, -π/2) x y y se mueven fuera de fase (es decir, hay una correlación negativa). En particular si φ xy = π o φ xy = -π se mueven en antifase. En ese caso, x y y están negativa y completamente correlacionadas; si φxy є (π /2 π), y lidera a x mientras que x lidera a y si φ xy є (-π, -π/2).
Con la diferencia de fase se puede calcular el tiempo de retardo instantáneo entre las dos series temporales
(14)
Donde ω(s) es la frecuencia angular correspondiente a la escala s.
Se ha realizado el análisis wavelet de forma separada para la relación entre LnGP/PIB-LnPIB y LnGP/PIB-LnPIBpc. Para utilizar este análisis para estudiar el rechazo o no de la ley de Wagner se deben considerar tanto la coherencia wavelet como las diferencias de fase. La coherencia wavelet entre las variables indica que la relación entre ambas es fuerte. Además, suponiendo que LnPIB (o bien LnPIBpc) determina LnGP/PIB, tal como se modeliza en las ecuaciones [1] y [2], LnPIB deberá estar positivamente correlacionado con LnGP/PIB y deberá liderar a LnGP/PIB (es decir φ xy є(- π/2,0))22. Además, si la ley de Wagner es relevante para explicar el crecimiento a largo plazo en el gasto público, entonces las regiones significativas de φ xy con LnPIB liderando coinciden con las regiones significativas del espectro de energía wavelet (WPS) de LnGP/PIB en el espacio tiempo frecuencia (gráfico 3).
Fuente: elaboración propia.
Gráfico 3 Espectro de energía wavelet de LnGP/PIB y coherencia wavelet entre LnGP/PIB y LnPIB
En la gráfica anterior se tiene, en el eje de abscisas, el número de años considerados (1850-2016) mientras que en el eje de ordenadas tenemos las frecuencias o períodos de tiempo en años. De esta forma, se puede realizar el análisis en el dominio tiempo-frecuencia. Las zonas amarillas denotan una fuerte correlación entre las dos variables mientras que las zonas verdes y azules denotan una correlación más baja. La línea blanca muestra el cono de influencia. Las áreas de alta frecuencia que se producen fuera o solapándose con el cono de influencia deberán interpretarse con precaución. Se puede considerar la coherencia wavelet como un coeficiente de correlación a lo largo del tiempo y a lo largo de la frecuencia. Por ello, se puede usar para detectar oscilaciones comunes localizadas en el tiempo en señales (series temporales) no estacionarias. En situaciones donde es natural ver que una serie temporal está influyendo en la otra, podemos usar las fases del espectro cruzado para identificar el retardo relativo entre las dos series. En la gráfica 3 se puedo observar cómo existe alta coherencia en el periodo entre uno y cuatro años en toda la muestra. Lo mismo ocurre entre cuatro y ocho años. Teniendo en cuenta este resultado se han calculado las fases y las diferencias de fase para las dos bandas de frecuencia en las que existe mayor coherencia entre las series temporales: la banda de frecuencia entre uno y cuatro años y la banda de frecuencia entre cuatro y ocho años. La gráfica 4 muestra los resultados.
Fuente: elaboración propia.
Gráfica 4 Fases y diferencias de fase para bandas de frecuencia entre uno y cuatro años y cuatro y ocho años
Tal como se ha analizado anteriormente, la diferencia de fase es φ xy є [−п, п]. Una diferencia de fase de cero, φ xy = 0 indica que las series se mueven juntas en la frecuencia especificada, es decir, están completa y positivamente correlacionadas; si φ xy є (0, π/2), las series se mueven en fase, pero la serie x precede a y; φ xy є (−π /2,0) entonces y precede a x. Una diferencia de fase de π (o -π) indica una relación antifásica; si φ xy є (π/2,π), y precede a x mientras que x precede a y si φ xy є (−π,−π/2)23. En la banda de frecuencia entre uno y cuatro años se producen pequeñas diferencias de fase entre las dos variables, aunque están en fase durante todo el período muestral. Observamos que la variable x (LnGP/PIB) lidera a y (LNPIB) entre 1850 y 1860, 1895 y 1905 y algunos pequeños intervalos. Solo se tiene un intervalo significativo entre 1960 y 1980 y de nuevo 1990 y 2016. Con esos resultados podemos rechazar la ley de Wagner para España en el período muestral considerado y la formulación dada.
En segundo lugar, se utiliza el análisis wavelet para estudiar la segunda ecuación. En este caso, las variables son LnGP/PIB y LnPIBpc. En el gráfico 5 se estudia la coherencia wavelet entre ambas variables
Al igual que en el caso anterior, tenemos fuerte coherencia entre las variables para las frecuencias entre 1 y 4 años y entre 4 y 8 años (gráfico 6). Teniendo en cuenta este resultado se han calculado las fases y las diferencias de fase para las dos bandas de frecuencia.
El resultado para la variable LnPIBpc es análogo al anterior. En la banda de frecuencia entre 1 y 4 años x lidera a y entre 1850-1865, 1895-1905, 1960-1985 y 1990-2016, con lo que solo tenemos períodos muy cortos en los que la variable x lidera a la variable y. Por tanto podemos rechazar, al igual que en el caso anterior, la ley de Wagner para el período completo. En consecuencia, usando esta metodología, podemos rechazar la ley de Wagner para España en el período y las formulaciones consideradas.
5. CONCLUSIONES
En este articulo se revisa brevemente la formulación original de la ley de Wagner. Aunque en su origen la ley parece de fácil comprensión, se ha producido, y aún se sigue produciendo, una gran controversia acerca de lo que dijo o quiso decir Wagner. Además, tomando como punto de partida la argumentación de Wagner se han formulado teorías alternativas tales como la hipótesis del efecto desplazamiento de PW y la de disparidad de Baumol.
El articulo realiza una doble contrastación empírica de la ley. Por una parte, se realiza la ya conocida contrastación de raíces unitarias y cointegración con rupturas estructurales y, por otra, la menos conocida metodología wavelet que se utiliza por primera vez en el contexto español. Ambas metodologías son bastante diferentes. En la primera podemos considerar un número limitado, y conocido de antemano, de cambios estructurales en los datos, mientras que la segunda metodología no limita el número de rupturas y se obtienen las mismas simultáneamente a los resultados.
El contraste se realiza utilizando un largo período muestral, 1850-2016. Al utilizar la primera metodología, no se pudo rechazar el cumplimiento de la ley en el largo plazo, mientras que la metodología wavelet encuentra numerosos puntos de ruptura y alternativas de precedencia del gasto público sobre el PIB y a la inversa, con lo que, aunque la ley se cumpla en pequeños intervalos, debe rechazarse de forma general. El resultado obtenido con la primera metodología está en la linea del de otros autores españoles (Díaz-Fuentes y Revuelta, 2013; Jaén-García, 2017 y 2018).
El resultado, utilizando raíces unitarias y cointegración, supone una relación entre crecimiento económico y gasto público. Una subida en el crecimiento económico implica una subida en el gasto público. Las razones pueden ser variadas. Un aumento en la población, en la necesidad de educación o salud supone un crecimiento en el gasto público. Esta relación puede ser directa pero también puede ser indirecta, pues una subida en los ingresos públicos, por ejemplo una subida en los ingresos impositivos, puede implicar una subida en el gasto utilizando la relación impuesto- gasto (Friedman, 1978).
