Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Cuadernos de Economía
versão impressa ISSN 0121-4772
Cuad. Econ. vol.32 no.spe61 Bogotá dez. 2013
A CHARACTERIZATION OF HEIGHT-BASED EXTENSIONS OF PRINCIPAL FILTRAL OPPORTUNITY RANKINGS
Stefano Vannucci1
1 Professor Stefano Vannucci, Department of Economics and Statistics, University of Siena, Piazza S.Francesco 7, Siena (Italy).
Abstract
A parameterized characterization of height-based total extensions of principal filtral opportunity rankings is provided and shown to include, as a special case, a version of the well-known Pattanaik-Xu characterization of the cardinality-based ranking.
Keywords: Opportunity sets, height, inequality.
JEL: D71, 025.Abstract
Se presenta una caracterización parametrizada de las extensiones totales basadas en altura, de los ordenamientos de oportunidad de filtro principal, y se demuestra que incluye, como caso especial, una versión de la reconocida caracterización de Pattanaik-Xu sobre el ordenamiento basado en la cardinalidad.
Palabras clave: conjuntos de oportunidad, altura, desigualdad.
JEL: D71, 025.
Résumé
Est présentée une caractérisation paramétrique des extensions totales, basées sur la hauteur, des ordonnancements d'opportunité de filtre principal, et il est démontré que cela inclut, comme cas spécial, une version de la fameuse caractérisation de Pattanaik-Xu sur l'ordonnancement basé sur la cardinalité.
Mots-clés : ensembles d'opportunité, hauteur, inégalité.
JEL : D71, 025.
Este artículo fue recibido el 6 de junio de 2013, ajustado el 12 de diciembre de 2013 y su publicación aprobada el 15 de diciembre de 2013.
INTRODUCTION
In the last two decades, a considerable amount of work has been devoted to the analysis of opportunity inequality and related issues concerning rankings of opportunity sets (see e.g. Alcalde-Unzu & Ballester, 2005; Alcalde-Unzu & Ballester, 2010; Arlegi & Nieto, 1999; Barberà, Bossert & Pattanaik, 2004; Dutta & Sen, 1996; Herrero, 1997; Herrero, Iturbe-Ormaetxe & Nieto, 1998; Kolm, 2010; Kranich, 1996; Kranich, 1997; Ok, 1997; Ok & Kranich, 1998; Pattanaik & Xu, 1990; Pattanaik & Xu, 2000; Savaglio & Vannucci, 2007; Savaglio & Vannucci, 2009; Sen, 1991; Xu, 2004, among many others). In particular, Savaglio and Vannucci (2007) suggest the introduction of minimal opportunity thresholds, modelling them by set-inclusion filtral preorders.
A set-inclusion filtral preorder on a finite set X of basic opportunities amounts to the standard set-inclusion partial order as augmented with a minimal opportunity threshold which is induced by an order-filter (to be defined below). Under the threshold, opportunity sets are indifferent to each other and to the null opportunity set, whereas, over the threshold the set-inclusion partial order is simply replicated. Therefore, the behaviour of a set-inclusion filtral preorder (henceforth SIFP) over the threshold is arguably non-controversial, at least in the following sense: if over the threshold, plausible preferences on opportunity sets are taken to be monotonic with respect to set-inclusion, SIFPs include their common core. On the other hand, since the threshold itself can be chosen in many different ways, SIFPsâunlike e.g. the cardinality preorderâalso accommodate a non-negligible diversity of judgments concerning the most appropriate ranking of opportunity sets. Thus, SIFPs can be regarded as a format for opportunity rankings that, building upon a common and essentially `objective' basis, gives some scope to a modicum of diversity in judgments, and therefore strikes a balance between any such judgment and the former common basis. Distinct choices of the relevant threshold enable an assessment of the extent of opportunity deprivation as seen from different perspectives. Furthermore, SIFPs are amenable to nice and strategy-proof aggregation methods including majority voting (see Savaglio & Vannucci, 2012; Vannucci, 1999). Therefore, even the threshold of any given SIFP may be possibly regarded as the outcome of a fair amalgamation of reliable information on private judgments of experts and/or stakeholders concerning the most appropriate choice of minimal living standards. Indeed, under a judicious selection of the set of basic opportunities, SIFPs arguably embody valuable information that is both reliable and comparatively easy to collect. That information can be deployed to assess several aspects of extant inequality and its social perception e.g. by majorization criteria. The implied assessments of the relevant opportunity distributions in terms of inequality and deprivation may in turn help diagnose those critical situations of severe inequality and polarization that could strain and erode several key social networks, and undermine social cohesion. All in all, carefully constructed SIFPs may arguably provide a key source of reliable and comparatively affordable information to several public and private agencies.
However, when it comes to using SIFPs as a key input for the assessment of opportunity inequality and polarization, one has to reckon with the central role of majorization rankings in the analysis of inequality. Hence, if inequality of opportunity profiles is to be assessed relying on a suitable majorization preorder, the very fact that a SIFP is, in general, a non-total preorder is undoubtedly a rather fastidious inconvenience. Two basic strategies may be devised to escape the foregoing difficulty while sticking to the notion of a majorization preorder, namely α) reformulating (and generalizing) the majorization construct in order to adapt it to the general case of arbitrary non-total preorders, or β) extending SIFPs to total preorders in a suitably 'natural' manner.
Strategy (α) is quite radical a move. Indeed, the main problem here is that majorizationâas it is usually conceivedârelies on comparisons between suitable sequences of pairs of partial numerical sums running over pairs of (α) equally sized subpopulations, each of which (β) forms a maximal chain with respect to the ranking of population units as induced by their respective individual endowments. Now, if the underlying preorder in endowment space is partial a typical joint effect of requirements (α) and (β) will consist in singling out distinct numbers of relevant partial sums at different opportunity profiles. But then, which partial sum of one opportunity profile should be compared to which partial sum of another one? It can be shown that, essentially, such a situation demands some special principled tactics to cope with pairs of non-isomorphic lattices of order filters as defined below. Thus, such an approach runs deep to the very foundations of the majorization construct.
By comparison, strategy (β) namely extending SIFPs to total preorders is much more conservative. One way to pursue strategy (β) is implicitly proposed and explored in Savaglio and Vannucci (2007). It consists in relying on the height function of a SIFP in order to extend the latter to a total preorder, resulting in the 'higher than' relation. Now, the height of an element x counts the size of the longest strictly ascending chain having x as its maximum. Does this notion qualify as a 'natural' extension of the underlying SIFP?
In general, the answer is admittedly bound to be disputable. In fact, the main problem here is that, generally speaking, SIFPs admit maximal strictly ascending chains of different sizes having the same minimum and the same maximum, i.e. SIFPs do not satisfy the so called Jordan-Dedekind chain condition, hence are not graded i.e do not have any rank function for their elements (see e.g. Barbut & Monjardet, 1970, for a general review of the foregoing notions as defined below in the text). Thus, reliance on height functions, which provide an instance of rank functions in the graded case, but are well-defined anyway, is a second-best choice of sorts. However, it turns out that in order to remedy that inconvenience, one may select a suitably defined well-behaved class of SIFPs. In the present paper, I focus on principal SIFPs, namely on those SIPFs whose threshold consists of precisely one minimum living standard (as opposed to a set of several mutually non-comparable minimal living standards). The reasons for doing so are the following. First, it is shown below that principal SIFPs are indeed graded and their height functions do amount to rank functions. This implies that in the principal case, heights provide a much more reliable numerical scale to rank the elements of a SIFP, than they do in the general case. Therefore, height-based extensions are arguably more 'natural' and strongly grounded for principal SIFPs than they are for general SIFPs. Second, Savaglio and Vannucci (2007) prove that principal SIFPs do support an opportunity-profile counterpart to the classic characterization theorems of the majorization preorder on real sequences due to Hardy, Littlewood and Pólya (1952).
Starting from the foregoing background and motivation, a simple characterization of height-based extensions of principal SIFPs is provided below. Our characterization relies on conditions that use the relevant filter as a fixed parameter. Indeed, it is quite clear that over the filtral threshold height-based extensions of principal SIFPs behave, essentially, as the cardinality-based preorder. Therefore, one should expect that a suitable reformulation of standard characterizations of the cardinality-based preorder would also work for height-based extensions of SIFPs. As a matter of fact, we show that SIFPs can indeed be characterized by a suitably adapted version of the axiom set employed by Pattanaik and Xu (1990) to obtain their well-known characterization of the cardinality-based preorder. We also show that in our setting a version of the Pattanaik-Xu characterization mentioned above is essentially recaptured as a special case which arises from a particular choice of the relevant filtral parameter. Arguably, that result highlights the significance of the cardinality-ranking as a benchmark and a limiting case within the larger family of SIFP-rankings, while confirming, at the same time, the remarkable scope and flexibility of SIFPs themselves.
MODEL AND RESULTS
Let (X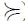 ) be a preset (i.e.
) be a preset (i.e. 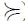 is a preorder, namely a reflexive and transitive binary relation on set X). We shall denote by
is a preorder, namely a reflexive and transitive binary relation on set X). We shall denote by 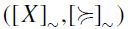 its quotient partially ordered set or quotient poset w.r.t. the symmetric component
its quotient partially ordered set or quotient poset w.r.t. the symmetric component 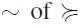 , namely the antisymmetric preset on the set
, namely the antisymmetric preset on the set 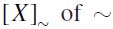 -equivalence classes as defined by the rule
-equivalence classes as defined by the rule 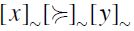 if and only if
if and only if  . If in particular
. If in particular  is antisymmetric then preset (X
is antisymmetric then preset (X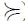 ) itself is a partially ordered set or poset. A (non-empty) antichain of (X
) itself is a partially ordered set or poset. A (non-empty) antichain of (X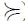 ) is a (non-empty) set
) is a (non-empty) set 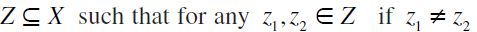 then
then 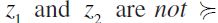 -comparable. For any (non-empty) antichain Z of a finite non-empty preset (X
-comparable. For any (non-empty) antichain Z of a finite non-empty preset (X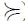 ) an order filter of
) an order filter of 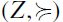 with basis Z is the minimal set
with basis Z is the minimal set 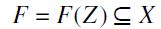 such that
such that 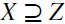 and for any
and for any 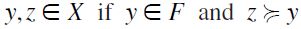 then
then 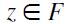 .
.
Thus, whenever X is finite, an order filter F of preset 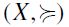 is uniquely defined by a finite set Z=Z(F) ={z1,...,zl} such that
is uniquely defined by a finite set Z=Z(F) ={z1,...,zl} such that 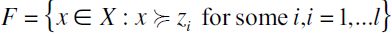 is also denoted as the basis of F.
is also denoted as the basis of F.
In particular, if Z is a singleton i.e. l=1 then F is said to be a principal order filter of 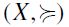 . It should be remarked that if
. It should be remarked that if 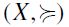 is a lattice (namely, if
is a lattice (namely, if 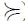 is antisymmetric and for any
is antisymmetric and for any 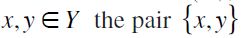 has both a least upper bound w.r.t.
has both a least upper bound w.r.t. 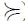 , and a greatest lower bound w.r.t.
, and a greatest lower bound w.r.t. 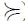 , denoted by
, denoted by 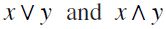 , respectively) then a principal order fillter of
, respectively) then a principal order fillter of  is also ∧-closed or equivalently a latticial filter, namely
is also ∧-closed or equivalently a latticial filter, namely 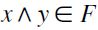 whenever both
whenever both 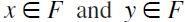 (it can also be shown that the converse also holds for any finite lattice).
(it can also be shown that the converse also holds for any finite lattice).
A chain of 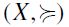 is a subset
is a subset 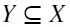 which is totally (pre)ordered by
which is totally (pre)ordered by 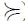 and such that for
and such that for 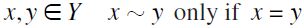 : by definition, the length of chain Y is
: by definition, the length of chain Y is 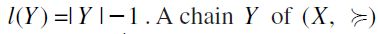 is maximal if there is no chain U of
is maximal if there is no chain U of 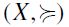 such that
such that 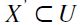 . If
. If 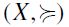 has a minimum or bottom element ⊥, one may define its height function
has a minimum or bottom element ⊥, one may define its height function 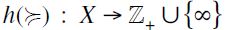 by declaring the height
by declaring the height 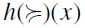 of any
of any 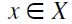 to be the lowest upper bound of the set of the lenghts of all (maximal) chains Y of
to be the lowest upper bound of the set of the lenghts of all (maximal) chains Y of 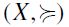 having x as their maximum.
having x as their maximum.
A preset 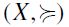 is said to satisfy the Jordan-Dedekind chain condition if for any
is said to satisfy the Jordan-Dedekind chain condition if for any 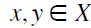 ,ï and any pair of maximal chains Y,Z of
,ï and any pair of maximal chains Y,Z of 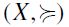 having x as their common minimum and y as their common maximum, l(Y)=l(Z) i.e. equivalently
having x as their common minimum and y as their common maximum, l(Y)=l(Z) i.e. equivalently 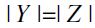 . Furthermore, a preset
. Furthermore, a preset 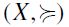 is graded if it admits a rank function i.e. an integer-valued function
is graded if it admits a rank function i.e. an integer-valued function 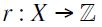 such that for any
such that for any 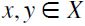 :
:
i) if 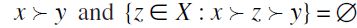 whenever x covers y i.e.
whenever x covers y i.e. 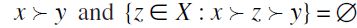 .
.
We are now ready to turn to set-inclusion filtral preorders. We shall confine ourselves to a finite set X, and its power set P(X). For any order filter F of poset 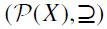 the F-generated set-inclusion filtral preorder (SIFP) is the binary relation
the F-generated set-inclusion filtral preorder (SIFP) is the binary relation 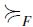 on P(X) defined as follows: for all
on P(X) defined as follows: for all 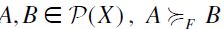 if and only if
if and only if 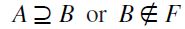 .
.
Let F be an order filter of 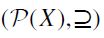 and
and 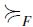 the (set-inclusion) filtral preorder induced by F.
the (set-inclusion) filtral preorder induced by F.
Then, the 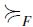 -induced height function
-induced height function 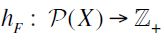 is defined as follows: for any
is defined as follows: for any 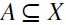 ,
,
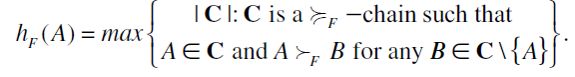
The height-based (total) extension of 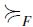 is the total preorder
is the total preorder 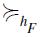 defined as follows: for any
defined as follows: for any 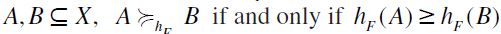 .
.
As mentioned in the Introduction, the main aim of the present paper is to provide a characterization of the height-based total preorder 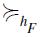 when the relevant order filter F is principal. Indeed, it turns out that in the latter case the SIFP
when the relevant order filter F is principal. Indeed, it turns out that in the latter case the SIFP 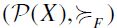 is graded, hence the height function hF is a well-defined rank function which provides an unambiguous criterion to assess the comparative 'status' of opportunity sets according to
is graded, hence the height function hF is a well-defined rank function which provides an unambiguous criterion to assess the comparative 'status' of opportunity sets according to 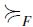 . This claim is made precise by the following
. This claim is made precise by the following
Proposition 1. Let F be a principal order filter of 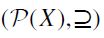 . Then, the F -generated SIFP
. Then, the F -generated SIFP 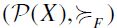 is a graded preset.
is a graded preset.
Proof. It is a well-known fact that a finite posetâhence indeed any finite preset, by definitionâis graded if and only if it satisfies the Jordan-Dedekind condition as defined above (see e.g. Barbut & Monjardet, 1970, chpt. 1, p. 39). Thus, it suffices to show that 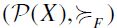 does satisfy the latter condition. Indeed, suppose it does not. Then, by definition there exist
does satisfy the latter condition. Indeed, suppose it does not. Then, by definition there exist 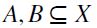 and maximal chains
and maximal chains 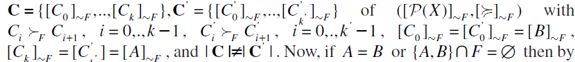 construction
construction 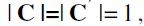 , a contradiction. Hence, A≠B and either
, a contradiction. Hence, A≠B and either 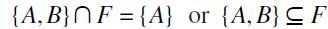 holds. If in fact,
holds. If in fact, 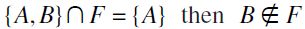 hence, by definition of
hence, by definition of 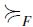 and maximality of chains C,C', it must be the case that both C1 and C'1 belong to the basis of F and for any
and maximality of chains C,C', it must be the case that both C1 and C'1 belong to the basis of F and for any 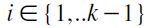 ,
, 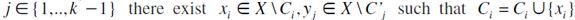 ,
, 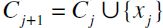 . But then, since F is principal, C1=C'1. It follows that, by construction,
. But then, since F is principal, C1=C'1. It follows that, by construction, 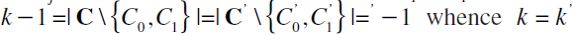 , a contradiction. Finally, if
, a contradiction. Finally, if 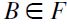 as well then again, by definition of
as well then again, by definition of  and maximality of chains C,C' it must be the case that for any
and maximality of chains C,C' it must be the case that for any 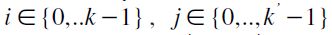 there exist
there exist 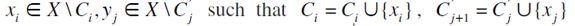 whence by the same argument presented above k=k', a contradiction, and the thesis is established.
whence by the same argument presented above k=k', a contradiction, and the thesis is established.
Remark. Of course, a general SIFP need not be graded. To check this fact, consider the following elementary example: let X={x,y,z}, F the order filter of 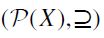 having {{x},{y,z}} as its basis, and
having {{x},{y,z}} as its basis, and 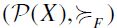 the resulting SIFP. Then consider
the resulting SIFP. Then consider 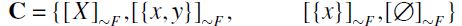 . Notice that C and C' are two maximal chains of
. Notice that C and C' are two maximal chains of 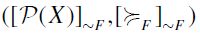 of different size (and length), having
of different size (and length), having 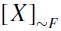 as their common maximum and
as their common maximum and 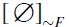 as their common minimum. Thus,
as their common minimum. Thus, 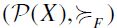 does not satisfy the Jordan-Dedekind chain condition and as a consequence -being finite- is not graded.
does not satisfy the Jordan-Dedekind chain condition and as a consequence -being finite- is not graded.
Let us now proceed to the announced characterization of 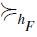 . In order to accomplish that task, a few more definitions are needed.
. In order to accomplish that task, a few more definitions are needed.
Let F be any (non-empty) principal order filter of the (finite) poset 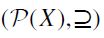 , i.e. equivalently a (non-empty) latticial filter of the (finite) lattice
, i.e. equivalently a (non-empty) latticial filter of the (finite) lattice 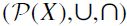 . Then, for an arbitrary binary relation
. Then, for an arbitrary binary relation 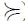 on P(X) (with asymmetric and symmetric components denoted as usual by
on P(X) (with asymmetric and symmetric components denoted as usual by 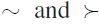 respectively) the following F-parameterized properties can be defined:
respectively) the following F-parameterized properties can be defined:
F-Restricted Indifference between Singletons (F-RIS):
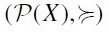 satisfies F-RIS if for all
satisfies F-RIS if for all 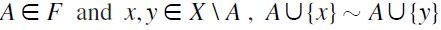 .
.
F-Restricted Strict Monotonicity (F-RSM):
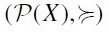 satisfies F-RSM if for all
satisfies F-RSM if for all 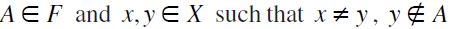 entails
entails 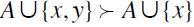 .
.
F-Restricted Independence (F-RIND):
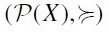 satisfies F-RIND if for all
satisfies F-RIND if for all 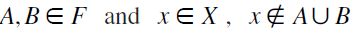 and
and 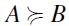 if and only if
if and only if 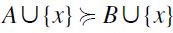 .
.
F-Threshold Effect (F-TE):
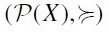 satisfies F-TE if
satisfies F-TE if 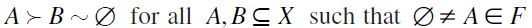 .
.
It turns out that, in general, the foregoing properties are not mutually independent. Indeed, we have the following:
Proposition 2. Let F be a principal filter of 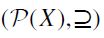 and
and 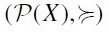 a preset which satisfies both F-RIS and F-RSM. Then
a preset which satisfies both F-RIS and F-RSM. Then 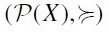 satisfies F-RIND as well.
satisfies F-RIND as well.
Proof. Let us assume that 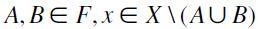 . Since, by definition of F, there exists Y
. Since, by definition of F, there exists Y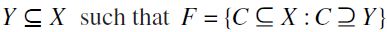 , it follows that there also exist non-negative integers h,k and
, it follows that there also exist non-negative integers h,k and 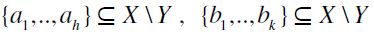 such that
such that 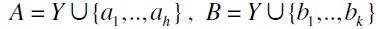 .
.
Now, suppose 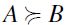 . If h < k then
. If h < k then 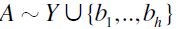 by a repeated application of F-RIS. Therefore, by a repeated application of F-RSM,
by a repeated application of F-RIS. Therefore, by a repeated application of F-RSM, 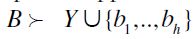
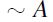 A whence, by transitivity of
A whence, by transitivity of 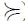 ,
, 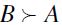 , a contradiction. Let us then assume without loss of generality that
, a contradiction. Let us then assume without loss of generality that 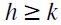 . Thus, by a repeated application of F-RIS to
. Thus, by a repeated application of F-RIS to 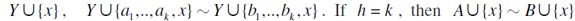 follows immediately. Otherwise,
follows immediately. Otherwise, 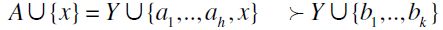 follows by a repeated application of F-RSM, and by transitivity of
follows by a repeated application of F-RSM, and by transitivity of 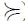 .
.
Conversely, let us assume that 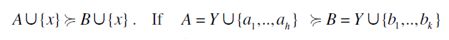 does not hold, then it must be the case that
does not hold, then it must be the case that 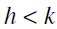 . But then, it follows by a repeated application of F-RIS to
. But then, it follows by a repeated application of F-RIS to 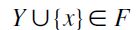 that
that 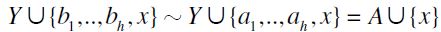 . Thus, by a repeated application of F-RSM and by transitivity of
. Thus, by a repeated application of F-RSM and by transitivity of 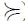 it also follows that
it also follows that 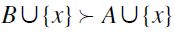 , a contradiction. Hence
, a contradiction. Hence 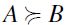 , and F-RIND holds.
, and F-RIND holds.
We are now in a position to state and prove the main characterization result of the present paper.
Theorem 3. Let F be a principal filter of 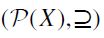 and
and 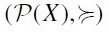 a preset. Then,
a preset. Then, 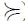 is the height-based (total) extension
is the height-based (total) extension 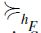 of the set-inclusion principal filtral preorder
of the set-inclusion principal filtral preorder 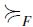 if and only if
if and only if 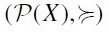 satisfies F-RIS, F-RSM and F-TE.
satisfies F-RIS, F-RSM and F-TE.
Proof. It is straightforward to check that 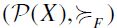 is in fact a totally preordered set that satisfy F -RIS, F -SM, and F -TE. Indeed, let
is in fact a totally preordered set that satisfy F -RIS, F -SM, and F -TE. Indeed, let 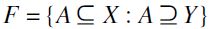 where
where 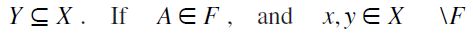 then by definition
then by definition 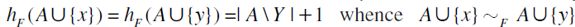 . Moreover,
. Moreover, 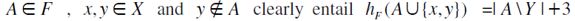 and
and 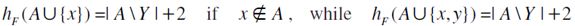 and
and 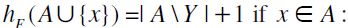 in any case, by definition,
in any case, by definition, 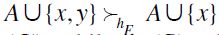 . Finally, for all
. Finally, for all 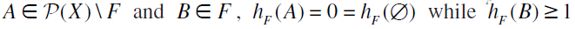 i.e.
i.e. 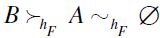 .
.
Conversely, let  be a preset that satisfies F-RIS, F-RSM and F-TE (hence in particular F-RIND by Proposition 2. To begin with, we define an auxiliary function
be a preset that satisfies F-RIS, F-RSM and F-TE (hence in particular F-RIND by Proposition 2. To begin with, we define an auxiliary function 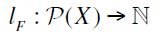 as follows: for any
as follows: for any 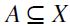 ,
, 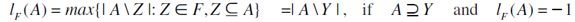 otherwise (i.e.
otherwise (i.e. 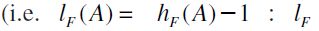 is the so-called length function of
is the so-called length function of 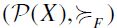 >.
>.
Next, we show that since 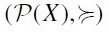 satisfies F-RIS and F-RIND it follows that for any A,B ∈ F:
satisfies F-RIS and F-RIND it follows that for any A,B ∈ F:
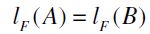 entails
entails 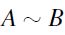 (or equivalently
(or equivalently 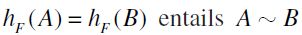 ).
).
We proceed by induction on lF(A). The case 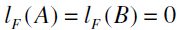 is trivial in that it entails - by definition - A=Y= B whence
is trivial in that it entails - by definition - A=Y= B whence 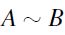 .
.
Let us now suppose by inductive hypothesis that for any nonnegative integer m not larger than n, 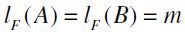 entails
entails 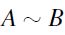 . Then, take a pair
. Then, take a pair 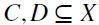 such that
such that 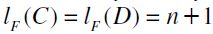 . If C=D there is nothing to prove. If C≠D then there exist
. If C=D there is nothing to prove. If C≠D then there exist 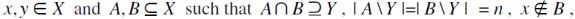 ,
, 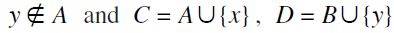 . It follows that
. It follows that 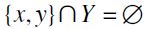 hence, by definition,
hence, by definition, 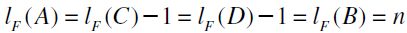 , which entails
, which entails 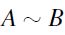 , by the inductive hypothesis. Moreover, if
, by the inductive hypothesis. Moreover, if 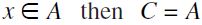 , a contradiction since
, a contradiction since 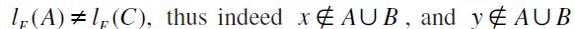 by a similar argument. Therefore,
by a similar argument. Therefore, 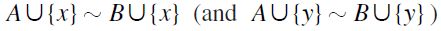 by F-RIND. Furthermore,
by F-RIND. Furthermore, 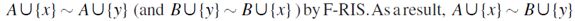 i.e.
i.e. 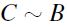 , by transitivity of
, by transitivity of 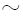 , and the inductive thesis follows.
, and the inductive thesis follows.
Now, take any pair 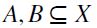 such that
such that 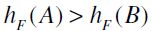 or equivalently
or equivalently 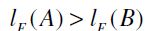 . Two cases should be distinguished, namely: i)
. Two cases should be distinguished, namely: i) 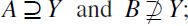 ; ii)
; ii)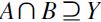 . If case 1) obtains, then, by definition of F, A
. If case 1) obtains, then, by definition of F, A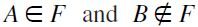 hence
hence 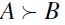 by F-TE. Under case 2) both
by F-TE. Under case 2) both 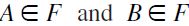 , and there exist
, and there exist 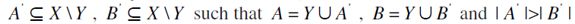 . Then, there also exists
. Then, there also exists 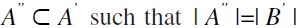 . We also posit
. We also posit 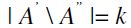 and
and 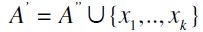 . Therefore,
. Therefore, 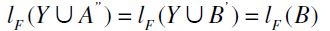 whence
whence 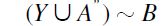 by the first part of this proof. Since
by the first part of this proof. Since 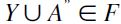 , it follows from F-RSM that Y
, it follows from F-RSM that Y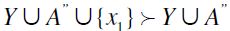 . By a repeated application of a similar argument - and by transitivity of
. By a repeated application of a similar argument - and by transitivity of 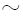 - we can eventually establish that
- we can eventually establish that 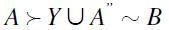 whence
whence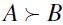 .
.
Thus, we have just shown that for any 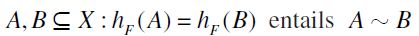 and
and 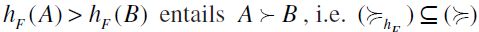 . Hence, in particular,
. Hence, in particular,  is a total preorder. But notice that if there exist
is a total preorder. But notice that if there exist 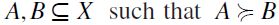 and not
and not 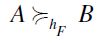 , then -since
, then -since 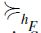 is also a total preorder by definition - it must be the case that
is also a total preorder by definition - it must be the case that 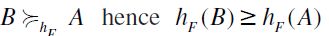 and therefore
and therefore 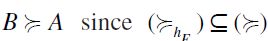 . Moreover, not
. Moreover, not 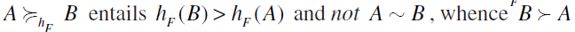 , a contradiction. It follows that
, a contradiction. It follows that 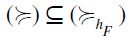 as well, so that
as well, so that 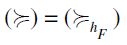 and our thesis is thus established.
and our thesis is thus established.
The foregoing characterization is tight. To see this, consider the following list of examples.
Example 1. Take a principal order filter F of 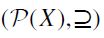 and the corresponding set-inclusion filtral preorder
and the corresponding set-inclusion filtral preorder 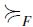 on P(X) defined as follows: for any
on P(X) defined as follows: for any 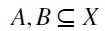
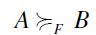 if and only if
if and only if  (see Vannucci, 1999; Savaglio & Vannucci, 2007). It is easily checked that
(see Vannucci, 1999; Savaglio & Vannucci, 2007). It is easily checked that 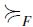 is indeed a preorder, and satisfies F-RSM and F-TE. Moreover, let
is indeed a preorder, and satisfies F-RSM and F-TE. Moreover, let 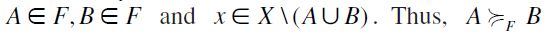 . Thus,
. Thus, 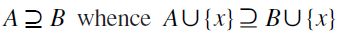 which in turn entails
which in turn entails 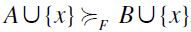 . Conversely, since obviously
. Conversely, since obviously 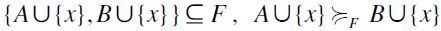 entails
entails 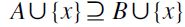 . Then
. Then 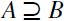 as well, hence by definition
as well, hence by definition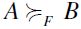 . It follows that
. It follows that 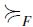 also satisfies F-RIND. However, for any
also satisfies F-RIND. However, for any 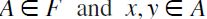 , such that
, such that 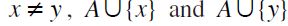 are not
are not 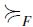 -comparable, hence F-RIS fails.
-comparable, hence F-RIS fails.
Example 2. Let us consider again a principal order filter F of 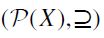 , and the binary relation
, and the binary relation 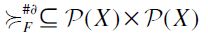 defined as follows: for any
defined as follows: for any 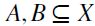
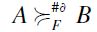 if and only if [either
if and only if [either 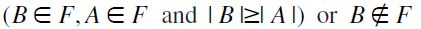 ]. Notice that
]. Notice that 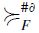 is indeed a preorder: to check this, first observe that reflexivity of
is indeed a preorder: to check this, first observe that reflexivity of 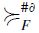 follows trivially from the definition, and assume that
follows trivially from the definition, and assume that 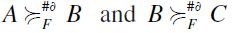 . The following mutually exclusive and jointly exhaustive cases should be distinguished:
. The following mutually exclusive and jointly exhaustive cases should be distinguished:
1) 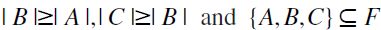 : in this case
: in this case 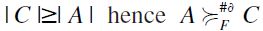 by the first clause; 2)
by the first clause; 2) 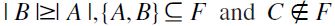 : in this case
: in this case 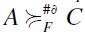 by the second clause; 3)
by the second clause; 3) 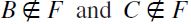 : here again
: here again 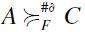 follows immediately from the second clause. Thus,
follows immediately from the second clause. Thus, 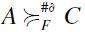 is transitive. Also, if
is transitive. Also, if 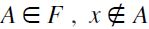 and
and 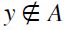 , then clearly
, then clearly 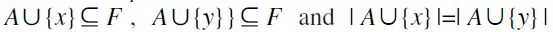 whence by definition
whence by definition 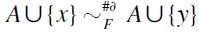 i.e. F-RIS is satisfied. Similarly, if
i.e. F-RIS is satisfied. Similarly, if 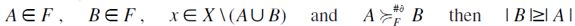 and
and 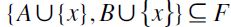 . Thus,
. Thus, 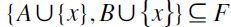 whence by definition
whence by definition 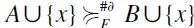 ". Conversely, if
". Conversely, if 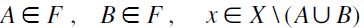 then, by definition
then, by definition 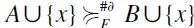 : it follows that
: it follows that 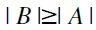 as well hence by definition
as well hence by definition 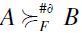 . Therefore, F-RIND is also satisfied by
. Therefore, F-RIND is also satisfied by 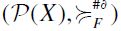 . Finally, F-TE follows immediately from the definition. However, F-RSM is definitely not satisfied by
. Finally, F-TE follows immediately from the definition. However, F-RSM is definitely not satisfied by  : indeed, if
: indeed, if 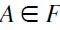 ,
,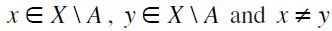 then, by definition,
then, by definition, 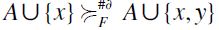 hence F-RSM is violated.
hence F-RSM is violated.
Example 3. Fix a principal order filter F of 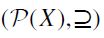 and take the binary relation
and take the binary relation 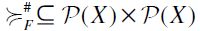 defined as follows: for any
defined as follows: for any 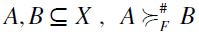 if and only if either
if and only if either 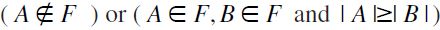 . It can be readily checked that
. It can be readily checked that 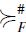 is a preorder: to see this, observe that reflexivity follows immediately from the definition. As for transitivity, if
is a preorder: to see this, observe that reflexivity follows immediately from the definition. As for transitivity, if 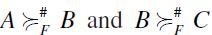 then the following two mutually exclusive and jointly exhaustive cases are to be distinguished: i)
then the following two mutually exclusive and jointly exhaustive cases are to be distinguished: i) 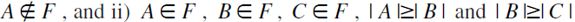 . In both cases,
. In both cases, 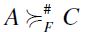 follows immediately from the definition. Furthermore, F-RIS and F-RSM of
follows immediately from the definition. Furthermore, F-RIS and F-RSM of 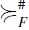 are also easily seen to follow trivially from the definition. On the other hand,
are also easily seen to follow trivially from the definition. On the other hand, 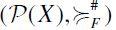 obviously fails to satisfy F-TE since by definition not
obviously fails to satisfy F-TE since by definition not 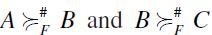 for any
for any 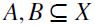 such that
such that 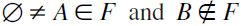 .
.
It should be emphasized here that the axioms used by Pattanaik and Xu (1990) in their well-known, and seminal, characterization of the cardinality-based preorder -namely Indifference between Singletons, Strict Monotonicity, and Independence- are implied by the corresponding axioms in our list when the reference filter F is taken to be the trivial or maximum filter P(X). Moreover, it is immediately visible that for F= P(X) the fourth axiom of our list i.e. F-Threshold Effect, which has no counterpart in the Pattanaik-Xu list, is, in fact, trivially satisfied when restricted to the original Pattanaik-Xu domain, which only includes non-empty opportunity sets. The remarkable flexibility and scope of SIFPs is thereby confirmed.
CONCLUDING REMARKS
As mentioned in the Introduction, the characterization of height-based extensions of principal filtral opportunity preorders provided in the present paper does not extend to the general case of arbitrary filtral opportunity preorders. This is due to the fact that when an order filter is not principal, the height function of the corresponding SIFP may exhibit a highly irregular behaviour.
Therefore, the height-based extension of a SIFP does not mimic the behaviour of the cardinality-based preorder over the filtral threshold. A simple example may help clarify this point.
Example 4. Let 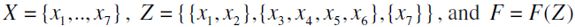 (notice that Z is indeed an antichain of
(notice that Z is indeed an antichain of 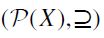 . Then, consider the height-based extension
. Then, consider the height-based extension 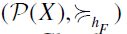 of the F-induced SIFP
of the F-induced SIFP 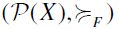 and take
and take 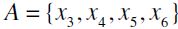 . Clearly,
. Clearly, 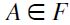 . However,
. However, 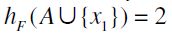 while
while 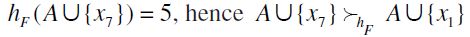 and F-RIS fails.
and F-RIS fails.
By contrast, our characterization is, in fact, amenable to a simple generalization in another direction. Indeed, a counterpart to Theorem 3 for arbitrary (finite) lattices of sets is readily available provided that the axioms are suitably reformulated by replacing join-irreducibles (elements that cover precisely one element) for singletons/atoms. The details of that extension, however, are best left as a topic for future research.
REFERENCES
[1] Alcalde-Unzu, J., & Ballester, M. (2005). Some remarks on ranking opportunity sets and Arrow impossibility theorems: Correspondence results. Journal of Economic Theory 124, 116-123. [ Links ]
[2] Alcalde-Unzu, J., & Ballester, M. (2010). On ranking opportunity distributions. Social Choice and Welfare, 34, 3-31. [ Links ]
[3] Arlegi R., & Nieto, J. (1999). Equality of opportunity: Cardinality-based criteria. In H. Swart (Ed.), Logic, game theory and social choice (pp. 458-481). Tilburg: University Press. [ Links ]
[4] Barberà, S., Bossert, W., & Pattanaik, P. K. (2004). Ranking sets of objects. In S. Barberà, P.C. Hammond & C. Seidl (Eds.), Handbook of Utility Theory, vol.II Extensions (pp. 893-977). Dordrecht: Kluwer Academic Publishers. [ Links ]
[5] Barbut, M., & Monjardet, B. (1970). Ordre et classification: Algèbre et combinatoire (Vol. I). Paris: Hachette. [ Links ]
[6] Dutta, B., & Sen, A. (1996). Ranking opportunity sets and Arrow impossibility theorems: Correspondence results. Journal of Economic Theory, 71, 90-101. [ Links ]
[7] Hardy, G., Littlewood, J. E., & Pólya, G. (1952). Inequalities (2nd Ed.). Cambridge: Cambridge University Press. [ Links ]
[8] Herrero, C. (1997). Equitable opportunities: An extension. Economics Letters, 55, 91-95. [ Links ]
[9] Herrero, C., Iturbe-Ormaetxe, I., & Nieto, J. (1998). Ranking opportunity profiles on the basis of the common opportunities. Mathematical Social Sciences, 35, 273-289. [ Links ]
[10] Kolm, S. C. (2010). On real economic freedom. Social Choice and Welfare, 35, 351-375. [ Links ]
[11] Kranich, L. (1996). Equitable opportunities an axiomatic approach. Journal of Economic Theory, 71, 131-147. [ Links ]
[12] Kranich, L. (1997). Equitable opportunities in economic environments. Social Choice and Welfare, 14, 57-64. [ Links ]
[13] Ok, E. (1997). On opportunity inequality measurement. Journal of Economic Theory, 77, 300-329. [ Links ]
[14] Ok, E., & Kranich, L. (1998). The measurement of opportunity inequality: A cardinality-based approach. Social Choice and Welfare, 15, 263-287. [ Links ]
[15] Pattanaik, P. K., & Xu, Y. (1990). On ranking opportunity sets in terms of freedom of choice. Recherches Economiques de Louvain, 56, 383-390. [ Links ]
[16] Pattanaik, P. K., & Xu, Y. (2000). On ranking opportunity sets in economic environments. Journal of Economic Theory, 93, 48-71. [ Links ]
[17]. Savaglio, E., & Vannucci, S. (2007). Filtral preorders and opportunity inequality. Journal of Economic Theory, 132, 474-492. [ Links ]
[18] Savaglio, E., & Vannucci, S. (2009). On the volume-ranking of opportunity sets in economic environments. Social Choice and Welfare, 33, 1-24. [ Links ]
[19] Savaglio, E., & Vannucci, S. (2012). Strategy-proofness and unimodality in bounded distributive lattices. Quaderni DEPS, 642. University of Siena. [ Links ]
[20] Sen, A. K. (1991). Welfare, preference and freedom. Journal of Econometrics, 50, 15-29. [ Links ]
[21] Vannucci, S. (1999). "Freedom of choice" and filtral opportunity rankings: Representation and aggregation. Quaderni DEPS, 274. University of Siena. [ Links ]
[22]. Xu, Y. (2004). On ranking linear budget sets in terms of freedom of choice. Social Choice and Welfare, 22, 281-289. [ Links ]













