Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.72 no.158 Medellín May/Aug. 2009
MODELACIÓN DE LA DISTRIBUCIÓN DE VIAJES EN EL VALLE DE ABURRÁ UTILIZANDO EL MODELO GRAVITATORIO
TRIP DISTRIBUTION MODELING AT ABURRA VALLEY USING THE GRAVITY MODEL
CARLOS GONZÁLEZ
Profesor Escuela Ambiental, Programa de Ingeniería Civil, Universidad de Antioquia, gonzalez@udea.edu.co
IVÁN SARMIENTO
Profesor Escuela de Ingeniería Civil, Universidad Nacional de Colombia Sede Medellín, irsarmie@unal.edu.co
Recibido para revisar marzo 13 de 2008, aceptado septiembre 24 de 2008, versión final octubre 10 de 2008
RESUMEN: El presente artículo se basa en los últimos estudios de transporte que se realizaron en el Área Metropolitana del Valle de Aburrá: Encuesta Origen/Destino 2005 y Estudio de rutas de buses, Modelación de la Red Vial del Valle de Aburrá, y Plan Maestro de Movilidad. Se realiza el análisis y desarrollo del modelo de distribución de viajes para el Área Metropolitana del Valle de Aburrá utilizando el software TransCAD con los datos del año 2005, utilizando el modelo gravitatorio, el cual determina los viajes que existen entre una y otra zona de acuerdo con la generación y la atracción de viajes que existen entre las zonas relacionadas y una función de impedancia que depende del tiempo de viaje entre zonas. Se analizó el modelo para diferentes períodos y motivos y se encontró que la función de impedancia que mejor se adapta al modelo estudiado es la exponencial negativa.
PALABRAS CLAVE: Modelación, Distribución de viajes, Modelo Gravitatorio.
ABSTRACT: This paper is based on recent studies of transportation which took place in the Metropolitan Area of the Aburra Valley: Survey Origin/Destination 2005 and Study of bus routes, the Road Network Modeling of the Aburra Valley, and Mobility Master Plan. The analysis and development of trip distribution model in the Metropolitan Area of Aburra Valley is done by using the software TransCAD for the database of 2005, using the gravitational model which determines the trips between two zones in accordance with the generation and attraction of trips between related zones and a impedance function that depends on the distance between zones, travel time or travel cost between zones. The model was analyzed for different periods and purposes and it was found that the negative exponential is the impedance function which adapts best to the studied model.
KEYWORDS: Modelation, Trip distribution, Gravity model.
1. INTRODUCCIÓN
Es esencial estudiar el transporte urbano como un componente de la ciudad y una función de ella. Éste debería garantizar que la accesibilidad de las personas a las distintas actividades se cumpla eficazmente a través de una adecuada movilidad ( en términos de tiempo y de costo monetario), por lo que es necesario que exista la adecuada conectividad físico-espacial que la haga posible, neutralizando el efecto negativo de la distancia. Para materializar estas funciones, el transporte debe auxiliarse al menos de dos instancias físicas principales: por una parte, de un sistema vial que asegure la conectividad entre los distintos espacios o zonas de la ciudad, y por otra, de un sistema de transporte que utilizando la infraestructura vial, permita el desplazamiento de las personas, entre sus lugares de origen y de destino.
Tradicionalmente se han considerado como variables que determinan el patrón geográfico de la movilidad de las personas en las ciudades a: los viajes generados por cada zona origen; los viajes atraídos por cada zona destino; y las resistencias dadas para la movilidad entre cada par de zonas (impedancias o funciones de desutilidad), empleando diversas formas funcionales que relacionan tales variables. La distribución de viajes es el proceso mediante el cual se determinan las zonas de origen de los viajes relacionados con un destino, y los destinos de los viajes generados en un origen.
En otras palabras, la distribución de viajes explica hacia qué zonas se dirigen los viajes producidos en cada zona. El objetivo del procedimiento de la distribución de viajes es sintetizar los enlaces de viajes entre orígenes y destinos, es decir, determinar cómo estos viajes se van a distribuir entre las diferentes zonas, para esto es necesario la distribución actual de viajes que se puede obtener por medio de encuestas origen destino y así obtener las matrices O/D.
Una vez conocida la matriz del año base, el problema principal radica en la utilización de esta matriz, para un año futuro de planeamiento cuyos viajes Pi (viajes producidos en la zona i) y Aj (viajes atraídos por la zona j) son conocidos. (Tij son los viajes de la zona i a la zona j) [1]. Por lo tanto, de lo que se trata es de llenar la matriz cuyos elementos deben cumplir:
 ;
; 
Para esto se han utilizado muchos modelos de distribución, los cuales se pueden agrupar en dos grandes grupos:
a) Modelos análogos o de factor de crecimiento:
- Método de factor uniforme
- Método del factor promedio
- Método Fratar
- Método Detroit
- Método Furness
Estos modelos son de poco uso en la actualidad, tienen su fundamento en el supuesto que la distribución de viajes futura será similar a la actual, siendo afectada por unos factores que representan el crecimiento previsto para las diferentes zonas, con el fin de obtener el número futuro de viajes entre ellas con base en la información de la matriz O-D del año base [2]. Sin embargo, tienen una gran utilidad en el ajuste de matrices sobre todo cuando se tiene información incompleta.
b) Modelos sintéticos:
- Modelo de gravedad
- Modelo electrostático
- Modelo de oportunidades
- Modelo de regresión lineal múltiple
Estos modelos sintéticos obtienen de las matrices O-D actuales, una serie de características de los viajes, a partir de los cuales puede predecir la distribución futura de ellos.
En general, todos los modelos se basan en el hecho de que el número de viajes entre zonas aumenta con el incremento de atracciones de dichos viajes, y se disminuye con el aumento de la resistencia dada entre ellos [2].
Los modelos de Distribución de Viajes, además de las variables explicativas de la movilidad, exigen la determinación de factores de ajuste asociados a cada zona Origen y a cada zona Destino de viajes, así como la calibración de parámetros que permiten determinar patrones geográficos de movilidad que parezcan razonables. Los valores de los factores de ajuste se hallan mediante procesos iterativos, partiendo de constantes iniciales, normalmente arbitrarias [3].
2. MODELO DE DISTRIBUCIÓN DE VIAJES
Un modelo de distribución trata de estimar el número de viajes en cada celda de la matriz, según la información disponible.
El proceso de modelación de la demanda de viajes en su etapa de distribución de viajes está condicionado a las demás etapas que la conforman ya que se puede plantear como un proceso iterativo simultáneo que se da debido a que el costo generalizado para viajar entre zonas está dado por la utilidad de viajar en cierto modo de transporte y depende además de la asignación del tráfico existente y de la red vial (tiempos y distancias), pero al tener en cuenta estas variables la distribución de viajes se puede modificar y por lo tanto las demás etapas también, repitiéndose el ciclo con base en los resultados encontrados en el reparto modal y la asignación de tráfico, devolviéndose a la distribución de viajes y repitiendo el proceso hasta encontrar el equilibrio en los viajes entre zonas.
El proceso de modelación de la distribución de viajes, es decir, el proceso que define cómo se van a distribuir los viajes de cada origen a cada destino de acuerdo a la impedancia que existe entre estas zonas, puede realizarse de varias maneras: por períodos y propósitos, por categorías socioeconómicas, por viajes motorizados, o combinaciones de ellos, entre otros. Esto depende de la necesidad de precisión que se tenga para el estudio y del objetivo del mismo.
Por otra parte, el procedimiento metodológico constituye una herramienta operativa que permite construir escenarios de desarrollo coherentes con los objetivos que impone el uso de modelos de transporte. Para poder modelar y evaluar distintas alternativas de proyectos de transporte es indispensable estimar la demanda que existirá por viajes en el mediano y largo plazo.
Para desarrollar la modelación de la distribución zonal de viajes en una ciudad sin más información que la que se tiene para el año base en la encuesta origen destino, se deben realizar los siguientes pasos teniendo previamente la información de la encuesta ya depurada, expandida y organizada [4].
- Clasificación de la información
- Calibrar el modelo
- Evaluar el modelo
El modelo gravitatorio es el más usado para modelar la distribución de viajes y supone que el número de viajes entre una zona i y un destino j es proporcional al número de viajes generados en la zona i, al número de viajes atraídos por la zona j y a una función de impedancia o de costos relativa a las zonas. Esta función de costos está relacionada con variables tales como: el tiempo de viaje, la distancia, el costo de viaje, etc. [5]. El modelo gravitatorio está representado mediante la ecuación:
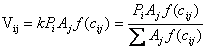 (1)
(1)
Donde,
: Viajes entre un origen i y un destino j
: Total de viajes producidos en el origen i
: Total de viajes atraídos en el destino j
Factor de fricción del viaje entre i y j k es una constante de proporcionalidad
Las funciones de impedancia (resistencias dadas para la movilidad entre cada par de zonas) mostradas en la tabla 1 pueden ser de los siguientes tipos: exponencial negativa, potencial inversa, gamma o funciones discretas [4].
Tabla 1. Funciones de impedancia
Table 1. Impedance functions
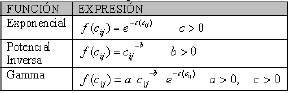
Donde a, b y c son constantes que deben calibrarse y cij es el valor de la impedancia en términos de la distancia, el tiempo o el costo de viaje entre la zona i y la zona j. 2.2 Información Necesaria Para La Calibración Del Modelo
Se debe tener la siguiente información básica para hacer la distribución de viajes:
- Un mapa con la zonificación de la ciudad
- Definir unos períodos y propósitos de modelación
- Matrices Origen Destino según período y propósito con todas las zonas de la ciudad (deben ser cuadradas)
- La red vial de la ciudad y velocidades medias de viaje
Se deben obtener de la base de datos del año base de donde se hizo la matriz diaria, otras matrices por período y por motivo (propósito), lo mismo que la matriz de tiempo entre centroides de las zonas, las cuales serán las futuras impedancias con las que se trabajará en el modelo. Con esta información se debe proceder así:
- Separar los viajes Basados en el Hogar (HB) de los viajes No Basados en el Hogar (NHB), por motivo y período.
- Obtener las matrices de viajes y de costos utilizando la información de las encuestas OD para cada uno de las clasificaciones efectuadas anteriormente. Esta matriz se considerará como referente de comparación para la modelación.
- Si no se cuenta con una matriz de tiempos se podría construir a partir de una matriz de distancias se puede obtener como la distancia entre centroides de cada zona y la matriz de tiempos se puede calcular como el tiempo promedio de viaje en todos los modos de zona a zona utilizando velocidades medias por modo.
- Por lo general los costos intrazonales son tomados por el software como cero, para ello se debe calcular una distancia intrazonal que es proporcional al área de la zona y tiempos de recorrido mínimo dentro de ellas.
Una vez obtenida la información para el año base se procede a la calibración del modelo mediante el siguiente procedimiento (con la ayuda de un software especializado como EMME/2 o TransCAD) [4]:
- Se elaboran las gráficas de las frecuencias de los costos medios para cada clasificación de viajes efectuada (en un caso urbano se utilizaría por ejemplo el tiempo de viaje) con el fin de tener una idea inicial del tipo de función de impedancia (gamma, exponencial, exponencial inversa, función discreta) que puede ajustarse a la distribución de costos para dicha clasificación, como se muestra en la figura 1.
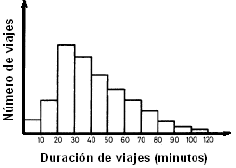
Figura 1. Distribución de tiempos de viaje
Figure 1. Trip Lenght Distribution
- Utilizando las matrices de viajes y de costos medios (tiempos medios) para el año base y la posible función de impedancia, se efectúan las iteraciones necesarias para obtener los coeficientes de calibración de la función de impedancia. En muchos casos el modelo no converge y por tanto, se hace necesario utilizar las funciones discretas, las cuales tiene una convergencia rápida. En estas se definen intervalos de costos (tiempos) y se obtiene una frecuencia de viajes para cada uno de ellos.
- El modelo puede converger para dos o más funciones de impedancia por lo que se debe elegir con base en la evaluación del modelo que se comenta a continuación.
Una vez calibrado el modelo se puede evaluar en condiciones presentes y/o futuras, para lo cual se requiere de los siguientes pasos:
- Obtener las generaciones y atracciones para el año base y para el año horizonte de planificación en cada una de las zonas definidas con los modelos de generación previamente calibrados.
- Calcular las matrices de costos medios (tiempos medios) para el año base.
- Efectuar la distribución de los viajes con la Ecuación del modelo gravitatorio para obtener la matriz de los viajes utilizando la función de impedancia (continua o discreta) obtenida de la calibración.
- Se debe obtener la matriz de viajes BH del período, sumando las matrices distribuidas de cada una de las clasificaciones realizadas para los viajes que son HB. Luego se obtiene la transpuesta de los viajes HB, la cual corresponde a los viajes de regreso a casa.. Una vez obtenidos los viajes de regreso a casa se suman con las matrices de viajes HB.
- Para obtener la matriz de viajes totales se suma la matriz de viajes HB obtenida en el paso anterior con la matriz NHB (suma de las matrices NHB).
- Obtener parámetros estadísticos como el R2 o para ver si la modelación es significativa comparando los viajes observados y modelados entre zonas y correlacionándolos. En este tipo de modelo no se alcanzan R2 muy altos, es decir, un valor adecuado podría ser por lo general mayor a 0.4.
3. MODELACIÓN DE LA DISTRIBUCIÓN DE VIAJES EN EL VALLE DE ABURRÁ
3.1 Definición del área de estudioEl área de estudio está dada por la Región Metropolitana del Valle del Aburrá. Ésta comprende los 10 municipios: Caldas, La Estrella, Sabaneta, Itagüí, Envigado, Medellín, Bello, Copacabana, Girardota y Barbosa y las subregiones vecinas. El Valle de Aburrá cuenta con una extensión total 184 km2 de área urbana y 965 km2 de área rural, donde se asientan aproximadamente 3.317.000 habitantes [6]. 3.2 Definición De La Zonificación
Considerando la Encuesta Origen destino de Hogares 2005 desarrollada por la Universidad Nacional de Colombia Sede Medellín para el Área Metropolitana, se definió una zonificación para el Valle de Aburrá: la zonificación interna abarca 409 zonas compatibles con las zonas SIT de la EOD-H 2005, incluyendo en zonas distintas los sectores urbanos y rurales de cada uno de los 10 municipios del Valle de Aburrá. La zonificación externa abarca 10 zonas, incluyendo en zonas separadas los municipios de Oriente y Occidente más cercanos y en forma agregada los municipios más lejanos. Sumando zonas internas y externas la zonificación a utilizar en el estudio comprende en total a 419 zonas [7]. En la figura 2 se muestra la zonificación.

Figura 2. Zonificación del área de estudio
Figure 2. Zoning of the study area
Es muy costoso simular todas las horas de un día en un sistema de transporte, dado que los modelos urbanos se calibran a nivel horario, es necesario conocer las horas del día donde se producen los comportamientos más representativos en términos de volúmenes de viajes, los cuales se denominan períodos de modelación; es decir, las horas pico o valles en los días representativos de los usuarios del sistema durante la semana. Para la modelación de la distribución de viajes en el Valle de Aburrá se definió el horario en las horas pico de la mañana y de la tarde ya que en estos períodos se presentan las horas más críticas del día en términos de congestión vial. En la tabla 2 se muestra la distribución horaria de viajes del Valle de Aburrá incluyendo los viajes a pie [4].
Tabla 2. Distribución horaria de viajes
Table 2. Distribution time travel

Observando los datos anteriores se puede inferir que los períodos pico representativos más críticos del día (aproximadamente el 40% de los viajes del día) los cuales se van a modelar son:
- Pico Mañana: de 6:00 a 8:00 hrs.
- Pico Tarde: de 17:00 a 19:00 hrs.
Existe una gran cantidad de viajes a la hora de almuerzo (12:00-14:00) que es una porción significativa de los viajes del día (15%). Sin embargo se trabajaron los dos períodos más críticos del día: el de la mañana y el de la tarde ya que son, por lo general, los horarios en los que la mayoría de las personas se desplaza en modos motorizados causando mayor congestión de tránsito vehicular: salen por la mañana de su hogar y regresan en la noche a él.
3.4 Definición De Propósitos De ViajesCon el fin de caracterizar apropiadamente los distintos tipos de viajes, se analizan de la Encuesta OD los motivos por los cuales estos se realizan y que inciden en la modelación del mismo.
Los propósitos más habituales de viajes son: Trabajo, Estudio y Otros y serán por lo tanto los considerados en el estudio.
El propósito de viaje Otros incluye todos aquellos viajes que no sean por motivo trabajo o estudio; es decir, de compras, por trámites, turísticos, recreacionales y de salud, por nombrar algunos.
3.5 Tipología De Viajes Por Propósito
Una forma frecuente de tipificar los viajes para efectos de sus análisis es el lugar donde se inician y donde se terminan; de esta manera se definen los viajes Basados en el Hogar como aquellos que el inicio o el término de viaje se da en el hogar, denominándose como Basados en el Hogar de Ida (BHI) los primeros o Basados en el Hogar de Retorno (BHR), los segundos. Los viajes cuyo origen o destino no es el hogar se denominan viajes no Basados en el Hogar (NBH). Cada una de estas tipificaciones tiene distintas especificaciones matemáticas para representarlos en el modelo de demanda de viajes. Así, los viajes basados en el hogar BHI ó BHR se dan principalmente en los períodos pico donde los usuarios del sistema salen de o llegan a sus hogares.
En el período pico de la mañana se modelaron sólo los BHI para el propósito estudio, trabajo y otros ya que representan el 97% de los viajes del período.
En el período pico de la tarde se modelaron sólo los viajes HBR al propósito Otros, en donde está el regreso a casa desde el estudio, trabajo y otros, ya que representan aproximadamente el 88% de los viajes del período.
El resto de viajes de cada período requiere de otro tipo de modelos de tipo regresión lineal relacionada con variables de atracción de las zonas y que están fuera del objeto de este estudio.
3.6 Red Vial Actual
La red vial actual de los municipios constituye un insumo fundamental en los análisis de transporte que se quieran hacer, por lo que ésta debió ser estudiada y evaluada para el Valle de Aburrá. En la figura 3 se muestra la red vial actual del Área Metropolitana [7].

Figura 3. Representación de la red vial para la modelación
Figure 3. Road network for modeling
La red incluye la numeración de zonas y nodos considerando una codificación que distinga entre municipios y otros criterios espaciales que permitan su fácil comprensión posterior, incluye además el tiempo a flujo libre para cada arco que corresponde a los resultados obtenidos directamente de terreno y tiempo a capacidad para cada arco que corresponde a los resultados obtenidos directamente de terreno [7].
Esta red vial principal define los caminos y rutas por los cuales se puede acceder a cada una de las zonas en las que se ha dividido el área de estudio, y debe ser complementada con enlaces entre ésta y el centro de las zonas, de forma que se cumplan los requisitos de los programas de computador que ayudan en la aplicación de los diferentes modelos de transporte. Estos enlaces son llamados conectores y complementan la relación entre las zonas y la red vial teniendo en cuenta la distancia de recorrido por las calles locales de cada zona.
3.7 Calibración del modelo de distribución de viajes en el área de estudio
Considerando que los viajes urbanos son dados por la distribuci ón espacial de los lugares de vivienda, trabajo, estudio, etc., así como los conceptos referidos en los numerales anteriores, el modelo de gravedad resulta ser el más apropiado para la distribución de viajes en el área de estudio.
Como se mencionó anteriormente, el modelo de gravedad determina los viajes que existen entre una y otra zona de acuerdo con la generación y la atracción de viajes que existen entre las zonas relacionadas y una función de impedancia que depende de la distancia de viaje entre las zonas, el tiempo de viaje o el costo del viaje.
De acuerdo con la experiencia en la estimación de modelos de transporte, las funciones de impedancia que normalmente se utilizan, y fueron utilizadas en la modelación se presentan en la tabla 1.
Gracias a los programas de computador que ofrecen una gran ayuda para la modelación del transporte, se consigue calibrar cada uno de las tres funciones: exponencial negativa, potencial inversa o gamma, entre las que se elige la mejor, para posteriormente determinar el modelo de gravedad que represente de la mejor forma la distribución de los viajes en la ciudad.
Se entiende entonces que es necesario conocer las distancias que existen entre las zonas en las que se ha dividido la ciudad y a partir de ellos obtener, el tiempo de viaje entre ellas o el costo del viaje. El procedimiento descrito anteriormente, permitió contar con esta información.
Se halló el TLD (Trip Lenght Distribution) para el área de estudio, los cuales fueron, en minutos:
- Minimum Trip Length : 0.431
- Maximum Trip Length : 104.255
- Average Trip Length : 12.118
- Standard Deviation : 11.810
En la figura 4, se muestra la curva de la distribución diaria de viajes por duración en el Valle de Aburrá en el 2005 a partir de la información hallada del TLD, la cual corresponde a la gráfica de una función exponencial negativa, la cual fue la función de impedancia elegida [4].

Figura 4. Distribución de viajes por duración en el Valle de Aburrá 2005 (Cada 5 min.)
Figure 4. Distribution of travel time in the Aburrá Valley 2005 (each 5 min.)
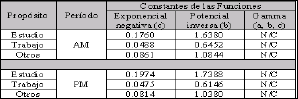
Se calibraron las tres funciones de impedancia descritas anteriormente por períodos y propósitos y se obtuvieron los valores de las constantes de las funciones respectivas, las cuales se muestran en la tabla 3. La función Gamma no converge (N/C) [4].
Tabla 3. Calibración de las funciones de impedancia por periodo y propósito
Table 3. Impedance functions calibrated by period and purpose
3.8 Evaluación del modelo de distribución de viajes en el área de estudio
Una vez calibrado el modelo se puede evaluar en condiciones presentes para lo cual se siguieron los siguientes pasos:
- Se obtuvieron las generaciones y atracciones para el año base en cada una de las zonas definidas con los modelos de generación.
- Se calcularon las matrices de costos medios (tiempos medios) para el año base.
- Se efectuó la distribución de los viajes a partir de la ecuación del modelo gravitatorio para obtener la matriz de los viajes presentes utilizando la función de impedancia obtenida de la calibración. Para un mejor ajuste se introducen factores kij para tratar de reproducir lo mejor posible las celdas de la matriz observada y no sólo el TLD.
- Se obtuvieron los parámetros estadísticos como el R2 para ver si la modelación es significativa comparando los viajes observados entre zonas y los viajes modelados entre zonas y correlacionándolos, como se muestra en la figura 5.

Figura 5. Correlación entre viajes Modelados Vs. Observados
Figure 5. Correlation between modeling trips Vs. Observed trips
Se evaluó el modelo para cada propósito y período con cada de las correspondientes funciones de impedancia que estaban calibradas y se compararon los viajes observados con los viajes modelados obteniendo el R2, los cuales se muestran en la tabla 4:
Tabla 4. Modelos según tipo de viajes evaluados por periodo y propósito
Table 4. Models based on type of travel evaluated by period and purpose

Se propone, en consecuencia con los resultados encontrados, efectuar la modelación de la distribución de los viajes, utilizando las matrices de impedancia de tiempos de viaje y la función de impedancias exponencial, con el parámetro de calibración (c), incluidos en los cuadros anteriormente indicados ya que convergen rápidamente y tienen mejor R2 que en la función potencial inversa [4]. Los valores de correlación obtenidos, permiten asegurar que el modelo encontrado, compuesto por los valores del parámetro c para la función exponencial, es adecuado para realizar la distribución de viajes en períodos pico en el Valle de Aburrá, a partir de los vectores de generación y atracción, proyectados en los diferentes escenarios de desarrollo futuro. El modelo elegido, con la función exponencial negativa, es el siguiente:

Donde,
: Viajes entre el origen i y el destino j
: Total de viajes producidos en el origen i
: Total de viajes atraídos en el destino j
:Factor de fricción del viaje entre i y j, de tipo exponencial negativo k es una constante de proporcionalidad
De esta forma se obtuvo la familia de modelos para los casos de los viajes mencionados al trabajo, al estudio y a otros para las dos (2) horas pico de la mañana y de la tarde, calibrados a partir de las matrices de viajes actuales observadas y en las referidas horas pico, obteniéndose así las matrices O/D modeladas.
Se encontró que en el modelo gravitatorio las impedancias dan una idea matemática mas no ingenieril de hacia dónde se realizan los viajes ya que depende de factores socioeconómicos y culturales de estas zonas además del propósito con que se esté viajando, es decir, el costo generalizado entre dos zonas lejanas, por ejemplo en el caso de Bello y Sabaneta, el costo es muy alto por la distancia entre ellos, el modelo hace que los viajes entre estas zonas sean mínimos y los ajusta con viajes de zonas cercanas como La Estrella, mas sin embargo para el propósito trabajo esto no se cumpliría, ya que si un grupo grande de personas viven en Bello y les toca ir a trabajar a Sabaneta, y lo seguirán haciendo aunque el modelo matemáticamente diga que no, por lo que siempre hay que usar constantes de ajuste k aplicados al modelo [4].
4. CONCLUSIONES
Las funciones de impedancia son fundamentales para el desarrollo de una buena distribución de viajes, éstas en lo posible se busca que empleen el costo generalizado. Sin embargo en este artículo se utilizó el tiempo de viaje como costo del viaje, lo cual es una buena aproximación a lo que percibe el usuario.
Para el Valle de Aburrá la función de impedancia que mejor se ajusta al modelo estudiado es la función exponencial en la cual se obtuvieron buenos valores de R2 (algunos R2 del orden de 0.9) que representan una buena relación entre viajes observados vs. viajes modelados en las horas picos de la mañana y de la tarde. La función potencial inversa también converge pero el ajuste no es tan bueno como el que presenta la exponencial. La función Gamma no converge en estos períodos.
Si se tiene la suficiente información de todas las etapas de la modelación, la metodología más avanzada es la de relacionar todas las etapas de viaje ya que es un modelo equilibrado con la demanda y la oferta y además validado con el resto de la información. Sin embargo, una modelación aislada de la distribución es aceptable cuando no se esperan grandes cambios en los usos del suelo de una ciudad.
Los factores k de ajuste para el modelo gravitatorio son fundamentales en el desarrollo de la aplicación del modelo ya que se basan en la matriz base para asemejar lo mayor posible los viajes modelados a los observados, de ahí un buen coeficiente R2.
REFERENCIAS
[1] ORTÚZAR, JUAN DE DIOS. Modelos de Demanda de Transporte. 2ª Edición. México. Ediciones Universidad Católica de Chile. Alfaomega. 2000. [ Links ]
[2] RAMÍREZ, O.F., SIERRA, N.L. Distribución de viajes en el proceso tradicional de planteamiento de transporte urbano. [Tesis de Grado]. Medellín. Universidad Nacional de Colombia. 1989. [ Links ]
[3] CÁRDENAS, D, COLOMER, J. Modelo de distribución geográfica de viajes, basado en el peso relativo de los atractores. Memorias VI Simposio de Ingeniería de Tránsito y Transporte. Universidad del Cauca. Popayán. Colombia. 2003. [ Links ]
[4] GONZÁLEZ, CARLOS. Modelación de la distribución de viajes en el Valle de Aburrá 2005. [Tesis de Maestría]. Medellín. Universidad Nacional de Colombia. 2007. [ Links ]
[5] ORTUZAR, J. WILLUMSEN, L. Modelling Transport. Second Edition. London. Jhon Wiley & Sons. U.K 1994. [ Links ]
[6] DANE. Censo Nacional de Población. Colombia. 2005. [ Links ]
[7] ÁREA METROPOLITANA DEL VALLE DE ABURRÁ. Formulación del Plan Maestro de Movilidad para la Región Metropolitana del Valle de Aburrá. Medellín. 2007. [ Links ]














