UN MECANISMO PARA LOCALIZACIÓN EFICIENTE Y EQUITATIVA DE NIMBY

A MECHANISM FOR EFFICIENT AND FAIR NIMBY LOCATION

 

FERNANDO A. CRESPO
Pontificia Universidad Católica de Chile, Profesor Departamento Ingeniería Industrial Universidad del Norte, facrespo@puc.cl

RICARDO D. PAREDES
Departamento de Ingeniería Industrial y Sistemas, Pontificia Universidad Católica de Chile, rparedes@ing.puc.cl

 

Recibido para revisar diciembre 28 de 2008, aceptado marzo 19 de 2009, versión final abril 14 de 2009

 

---

RESUMEN: Los NIMBY (Not In My BackYard) son localizaciones que por ser socialmente necesarios por una parte, pero indeseables por las localidades que los hospedan por otra, tienden a ser rechazados, los costos verdaderos son escondidos por las comunidades y finalmente, son asignados en base de presiones corporativas, sin criterios técnicos y con sesgos en contra de las localidades más pobres. En este trabajo proponemos un mecanismo de localización de NIMBY descentralizado, y que cumple con los objetivos de: asignar a las comunidades de menor costo (eficiente), ser equitativo (compensa a la comunidad afectada), presupuesto balanceado, y cumple con las condiciones de racionalidad individual.

PALABRAS CLAVE: NIMBY, diseño de mecanismo, localización de instalaciones, subastas.

ABSTRACT: Whilst NIMBY (Not In My BackYard) are facilities necessary to society, are rejected for communities that host them. Thus, in contexts where bad compensation mechanisms exist, communities do not reveal the cost of hosting and social evaluation is severely limited. That explains why NIMBYs are finally located in base of corporate pressures, without technical criteria and with bias against the poorest localities. We propose decentralized mechanism to locate a NIMBY that I efficient (the NIMBY goes to the lowest cost location), and fair (all communities, including the host, are not worse off). The mechanism has balanced budget, and it fulfill the conditions of individual rationality.

KEYWORDS: NIMBY, mechanism design, localization, auctions.

---

 

1. INTRODUCCIÓN

Se entiende por NIMBY ('Not In My BackYard') aquellas instalaciones que son consideradas socialmente necesarias, pero que son rechazadas por las comunidades potencialmente hospedadoras [1]. Ejemplos de NIMBY son los vertederos, cárceles, aeropuertos, centrales de energía nuclear, y centrales termoeléctricas. La relevancia de los NIMBY como materia de análisis se ha intensificado en los últimos años como consecuencia de los problemas asociados al cambio climático, a las políticas ambientales, y a la localización de desechos, entre otros [2].

Debido a esta doble particularidad, ser necesarios socialmente pero indeseables localmente, el problema de localización es pertinente. Ellos son habitualmente resistidos y en particular, en lugares socialmente adecuados. Más aún, las decisiones de localización se toman bajo ambientes de presión y lobby ([3],[4]), y raramente cuentan con un apoyo en criterios técnicos. Con ello, no sólo se compromete la eficiencia, sino que también la equidad.

La literatura se ha concentrado, original y preferentemente en la razón política de la resistencia de las comunidades para aceptar hospedar un NIMBY (véase, por ejemplo, [3], [[6], [7], [8] y [9]). Desde luego, ello es predecible cuando, como habitualmente ocurre, no hay compensaciones a las comunidades huéspedes. Sin embargo, aún en contextos de compensación, la resistencia suele permanecer. El pago de compensaciones y su forma son determinantes para que las decisiones de localización sean percibidas como justas [5], [7].

Por su impacto social, los NIMBY pueden concebirse parcialmente como un bien público, donde si bien los consumidores no pueden ser excluidos del servicio, si generan externalidades negativas a quién lo aloja [10], lo que restringe dicho planteamiento.

Por cierto, las compensaciones pueden ser una solución al problema de aceptación, pero persiste la necesidad de la asignación. Idealmente, una asignación eficiente requeriría conocer el costo que el NIMBY tiene para la comunidad que lo aloja. Si tal costo es información que sólo la comunidad conoce, entonces se requiere que existan incentivos a revelar los costos. Consecuentemente, un mecanismo eficiente requiere ser incentivo compatible para que la solución sea Pareto eficiente ([11], [12], [13]). Por otra parte, los beneficiados del NIMBY, como en la provisión de bienes públicos, deben participar en el pago de transferencias, de modo de evitar free-riding (véase, [12] y [14] para compatibilidad de incentivos en equipos).

La literatura muestra que un mecanismo que obtiene la revelación de los costos verdaderos de las comunidades, requiere transferencias y compensaciones del tipo Groove ([11], [12], [14], [15], [16], [17]). De aplicarse el resultado al NIMBY, impone que las transferencias y la compensación dependen de los costos declarados por las demás comunidades pero no del costo declarado propio. En este contexto, la fórmula de compensación es difícil de entender, lo que la limita en una aplicación real.

Además, las transferencias tipo Groove, que han alimentado modelos propuestos para resolver la asignación del NIMBY (e.g., [1], [18], [19], [20]), tienen el problema de que generan presupuestos desbalanceados ([12], [14]). El principal problema de los presupuestos desbalanceados es que inducen a la colusión por algunas de las partes. Más aún, en el caso de un déficit financiado por el planificador central, la necesidad de financiamiento requeriría levantar impuestos que también generan una pérdida social.

En el caso que la información de costos provenga fundamentalmente de las comunidades y ella deba ser obtenida a partir de sus propias declaraciones, una forma natural de aproximarse al problema es que los mecanismos de localización se diseñen sobre la base de subastas.

Pero se tiene evidencia empírica que el NIMBY es un bien cuya disposición a pagar (willingness to pay, WTP) no está alineada con la disposición a aceptar tenerlo (willingness to accept, WTA) ([19], [9]), lo que requiere formular la consulta en términos de la disposición a no alojar el NIMBY.

Kunreuther y Kleindorfer [19] proponen un mecanismo que requiere que el Planificador Central conozca los costos de cada comunidad de tener un NIMBY, más el beneficio cruzado, para cada comunidad, de que lo tengan las otras comunidades. Resuelven la localización mediante una solución max-min, pero el mecanismo genera un superávit al planificador. La falla más obvia de esta solución, aparte que genera un superávit, es que el problema del NIMBY es precisamente que induce a las comunidades a no revelar los costos, información que es privada.

En Sullivan [21] el Planificador decide la localización por lotería, lo que no sólo aumenta potencialmente la probabilidad de rechazo, sino que no resuelve el problema de equidad asociado. En O´Sullivan [22] se plantea un mecanismo con compensación y transferencia, donde se asigna al mínimo costo declarado y se compensa con el promedio de las declaraciones. El mérito del mecanismo es el único que a nuestro conocimiento que resuelve el problema de asignación de NIMBY concompensación y transferencia, sin traspasar superávit al planificador. Un problema, sin embargo es que su diseño es para el caso de dos comunidades, lo que reduce el alcance práctico y la generalidad del resultado. En esta línea, está también el mecanismo propuesto en Jean-Marie et al. [23].

Los mecanismos propuestos en Coursey y Kim [1] y Kim [18], resuelven la asignación del NIMBY a través de una subasta tipo Vickrey, donde el valor es asignado al menor costo pero se compensa con el segundo mayor valor. Cada parte paga una transferencia constante que es proporcional al mínimo valor propuesto. Sin embargo, como se demuestra en [24], este tipo de asignación es ineficiente e implica un déficit del planificador, lo que lo hace, además, susceptible de colusión.

El mecanismo de Minehart y Neeman [20] es similar al presentado en [1] y [18], con la diferencia que las transferencias son proporcionales al valor mínimo. En este caso, sin embargo, el factor de proporcionalidad necesita información externa que, para los objetivos de nuestro análisis, no abordan el problema básico de la falta de revelación de información al planificador.

Así, la literatura muestra que no hay un mecanismo que reúna las condiciones de ser eficiente, incentivo compatible (que se requiere la revelación de costos verdaderos por parte de las comunidades), que tenga condiciones de racionalidad individual y que conserve el presupuesto balanceado [25]. Dado que el resultado de [25] imposibilita un mecanismo con dichas propiedades, la idea es encontrar uno que aproxime las propiedades ideales. Este mismo problema es tratado en otro contexto [26], donde también se plantea un mecanismo que aproxima las condiciones de un mecanismo ideal.

El mecanismo que proponemos en este artículo cumple con tres de las condiciones necesarias. Concretamente, el mecanismo consiste de un juego de dos etapas. Por una parte el planificador pone las reglas de asignación, de pago de compensación y transferencias. Con ellas, las comunidades declaran en cuanto valoran un NIMBY. Con los costos declarados, y según las reglas de asignación previamente establecidas, el planificador asigna el NIMBY.

En lo que sigue, describimos el mecanismo, y mostramos que logra la eficiencia, mantiene el presupuesto balanceado, y cumple con las condiciones de racionalidad para garantizar que los individuos no rechacen las asignaciones. Aunque en general el mecanismo no permite una revelación del verdadero costo para cada comunidad, permite al planificador obtener el ranking de los verdaderos costos, lo que es una condición suficiente para la asignación eficiente.

 

2. MECANISMO DE LOCALIZACIÓN DEL NIMBY Y COMPENSACIÓN

En términos simples, el mecanismo que analizamos opera en dos etapas. En primer lugar, las comunidades declaran sus disposiciones a recibir el NIMBY a cambio de una compensación (lo que denominamos costo declarado), en un proceso análogo a una subasta y el planificador central asigna el NIMBY a la que declara menor costo. En segundo lugar, la comunidad alojadora es compensada en la cantidad que ha declarado, recurriendo a un fondo generado por el aporte de cada una de las otras comunidades que pagan una fracción del costo mínimo y que es proporcional a su propia oferta.

En lo que sigue, analizamos este mecanismo en función de su capacidad para generar un equilibrio eficiente ([14], [27]).

2.1 Supuestos del Mecanismo
Siguiendo parcialmente a [1], suponemos:

A1. El objetivo del Planificador Social es maximizar el bienestar social, medido como la suma de las utilidades esperadas de todas las comunidades.

A2. El costo de construir el NIMBY, es independiente de su localización, y no forma parte de los costos que deben evaluar las comunidades.

A3. Todas las comunidades son neutrales al riesgo y cada comunidad tiene una utilidad:

donde es 1 si la comunidad i aloja el NIMBY y 0 si no, es el costo que declara la comunidad i cuando participa del mecanismo para la localización del NIMBY (). es el costo verdadero. es la transferencia que pagaría i a la comunidad que recibe el NIMBY, y es la compensación que recibiría la comunidad i si ella aloja el NIMBY.

Agrupando los valores constantes, se obtiene:

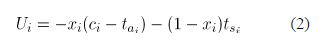
donde (2) =(1)+, y esta última parte es constante, y el costo declarado se supone definido en un conjunto , donde en otras partes se denomina a dicho conjunto como ([1], [18]).

A4. Todas las comunidades conocen sus costos y las reglas del mecanismo, pero no conocen los costos de las otras comunidades.

A5. No hay colusión entre las comunidades.

A6. Las comunidades no pueden salirse del juego.

De (2) se puede deducir las condiciones de racionalidad, de acuerdo a [28]. Despejando (2) se obtiene:

Matemáticamente, el modelo de maximización del Planificador y sus restricciones son:

Modelo 1 OP:

donde (OP.1a) implica presupuesto balanceado; (OP.1b) indica que el NYMBY se instalará en una sola comunidad; (OP.1c) indica que la localidad que aloja el NIMBY no transfiere fondos, y las que transfieren cumplen la condición de racionalidad (3); (OP.1d) indica que la localidad que aloja el NIMBY es la única que recibe compensación y mayor o igual que su oferta; (OP.1e) implica una solución factible al problema, y (OP.1g) indica que la variable de localización es binaria, y tendrá un valor 1 para la comunidad i que aloje el NIMBY, y 0 para las demás.

Notamos los costos ordenados como .

El Teorema 1 establece las condiciones a las cuales al planificador le va a convenir plantear la asignación del NIMBY.

Teorema 1: Solución de maximización del Modelo 1 OP. Para el Modelo 1 OP entendemos el dominio D como todos los puntos que cumplen las restricciones (OP.1a)-(OP.1g). Como D es cerrado y acotado, con entonces el Modelo 1 OP tiene solución óptima, y la solución óptima es:

Dem: Para ver que , un punto factible es asignar al mínimo, y que pague solamente el de mayor oferta. Si la suma a maximizar de (OP) se descompone y se reemplaza (OP.1a) en la función objetivo, sólo quedaría maximizar sobre la suma negativa de costos, en un conjunto con puntos finitos que elegir. Entonces, lo más eficiente es asignar en la comunidad de mínimo costo declarado. 

Una conclusión del Teorema 1, es que para el planificador, la función objetivo del modelo es una decisión de localización que depende siempre del costo que declaren las comunidades, y que es eficiente si la asigna al mínimo costo declarado, con una regla que mantenga el presupuesto balanceado, y las condiciones de racionalidad individual.

Es necesario notar, que los costos que declaren las comunidades dependen de la regla de compensación y transferencia, donde descubrir los costos que declararán las comunidades constituye la segunda etapa en la demostración, pero es la primera en términos temporales, dado las reglas que establezca el planificador condiciona las declaraciones de las comunidades. Otra conclusión es que para el planificador, hay infinitas combinaciones de indemnización posible, que mantienen el presupuesto balanceado, y que asignan al costo mínimo. Para el mecanismo de este artículo, escogimos una regla particular.

2.2 Equilibrio de Nash
En esta etapa, se estudiará el efecto del mecanismo sobre las declaraciones de costos por parte de las comunidades, cuando el planificador toma la decisión de localización de acuerdo al Modelo 1 OP.

Definición 1: Definimos equilibrio de Nash no cooperativo como , tal que:

donde son los espacios de estrategias.

2.2.1 Comunidades sin conocimiento del costo del resto

Teorema 2: Existencia de un equilibrio de Nash cuando las comunidades no tienen ninguna información acerca de los costos de otras comunidades.

En primer lugar, cada comunidad i declara un costo , donde es la verdadera disposición real a pagar por no alojar el NIMBY. Para la comunidad i, definimos la función de utilidad con :

En segundo lugar, el planificador central resuelve el problema de optimización del Modelo 1 OP.

Cabe remarcar que los vectores de variables de decisión los hemos expresado en función de los costos declarados, de manera que se tiene que , y .

Conservando las condiciones establecidas en [1], en un juego en el cual establecemos la siguiente política de solución:

existe un equilibrio de Nash como el enunciado en la Definición 1.

Dem: Del Teorema 1, sabemos que el modelo 1 OP tiene solución óptima en el mínimo cuando se tiene presupuesto balanceado con condiciones de racionalidad individual, y que las condiciones impuestas en (7) las cumplen, por lo que son solución del Modelo 1 OP. La siguiente etapa es demostrar que las funciones de utilidad (6) con el dominio expresado en (5) son cóncavas para . Las reglas para asignar y son:

Reemplazando (8) en (6), requerimos demostrar que (6) es cóncava bajo . Como varía de acuerdo a los , reemplazamos por:

(9) Corresponde a la regla de asignación del NIMBY, ya que en i cuando es máximo, entrega la misma solución del Modelo 1 OP, y la función (9) tiene la característica de que cuando , es decir, el mínimo es descubierto desde los valores.

Reemplazando (8) y (9) en (6) se tiene:

con .

Con ello se observa que y que <0, luego es cóncava [29]. Consecuentemente, como el Modelo 1 OP tiene solución, y es cóncava, existe al menos un equilibrio de Nash [30].

Teorema 3: Estrategias óptimas cuando las comunidades no tienen ningún conocimiento sobre los costos de otras. Asumiendo que , donde , y bajo los mismos supuestos del Teorema 2, la estrategia óptima de las comunidades es:

esto es, el mecanismo de localización bajo neutralidad al riesgo es eficiente y compatible de incentivos, ya que todas las comunidades revelarían sus verdaderos costos.

Dem: Para cada comunidad el problema de maximización es:

Planteando las condiciones de Karush-Kuhn-Tucker [29] tenemos:

Como la solución simultánea de la N ecuaciones depende de , que es positiva, el máximo se alcanza cuando (despejar de (13)(ia)), y ello ocurre donde .

Necesitamos encontrar el del costo declarado, para saber la diferencia entre ese costo y el costo verdadero para cada comunidad, para ello planteamos el siguiente modelo:

Modelo 2 DM:

donde (DM.i) es la condición de Nash.

Aplicando las condiciones de Karush-Kuhn-Tucker para el Modelo 2 DM tenemos:

Como , en (14)(ia) se tiene que , luego para que , entonces .

Resolviendo para las N comunidades, concluimos que . 

Consecuentemente, los Teoremas 1, 2 y 3 demuestran que el mecanismo propuesto, cuando las comunidades no tienen información de los costos de las otras comunidades, declararían su verdadero costo o disposición a recibir el NIMBY.

2.2.2 Comunidades con algún conocimiento sobre la distribución de los costos
El caso analizado en 2.2.1 no es totalmente realista, porque si bien en la práctica, cada comunidad puede desconocer el costo de otras, sí puede tener una idea, un orden de magnitud, de tales costos. Consecuentemente, una pregunta que surge naturalmente es cómo cambian los resultados previos cuando las comunidades, desconociendo la disposición específica a alojar el NIMBY de las otras comunidades, sí cuentan con alguna información que les permite tener una idea de ese costo. A modo de ejemplo, el costo de alojar un NIMBY pueda ser proporcional al valor de la tierra (conocido), más un componente aleatorio, desconocido para las otras comunidades.

Suponemos aquí que cada comunidad conoce su propio costo y que en relación al resto, le atribuye un valor asociado a una probabilidad. Este caso generaliza el supuesto A4, ya que el desconocimiento en juegos se puede representar mediante distribuciones de probabilidad. Específicamente, suponemos que cada comunidad diferente de , estima que la distribución de costo de la comunidad es .

Definición 2: Equilibrio de Nash Bayesiano. Siguiendo [15], dado los espacios de estrategias y , un equilibrio de Nash Bayesiano No Cooperativo es definido como:

donde 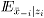es la esperanza condicional de los costos de todas las comunidades excepto i, dado el costo declarado por la comunidad i.

Teorema 4: Existencia de equilibrio de Nash cuando las comunidades tienen conocimiento incompleto y común sobre los costos de las otras.

Como señalamos, en la primera etapa, cada comunidad i declara un costo , y el resto de las comunidades visualiza para esa comunidad una distribución con densidad . Para la comunidad i, definimos la función de utilidad con :

donde es la esperanza condicional que cada comunidad asume, e es la función indicadora en el segmento escogido.

En la segunda etapa, el planificador resuelve el problema de optimización del Modelo 2 OP:

donde es el costo declarado por la comunidad i. Nótese que el Modelo 2 OP es el mismo que el Modelo 1 OP, porque el planificador sólo puede asignar de acuerdo al costo declarado. es la distribución conjunta respecto de todas las comunidades de que sea mayor que el valor mínimo, y es la que se usa para calcular la función esperada de utilidad (17). Su densidad se nota .

De acuerdo con las condiciones establecidas para que exista un equilibrio de Nash según [30], existe un equilibrio de Nash como el enunciado en la Definición 2 en un juego en el cual establecemos la siguiente política de solución:

Dem: Del Teorema 1, sabemos que el modelo 2 OP tiene solución óptima en el mínimo, y que las condiciones impuestas en (18) mantienen el presupuesto balanceado y respetan las condiciones de dicha solución óptima, por lo que son solución del Modelo 2 OP. Por otra parte la distribución conjunta de la comunidad dado los probables costos declarados por las demás comunidades es:

De (19) se puede obtener su densidad

con (20) la función de utilidad (17) se puede expresar como:

Del Teorema 2 se sabe para (que está dentro de la integral) que y que es negativa, luego el índice de aversión al riesgo es positivo por lo que las comunidades son estrictamente adversas al riesgo, por lo tanto existe al menos un equilibrio de Nash, que cumple con la Definición 2. Conjuntamente que con los costos declarados y las reglas establecidas en (18) el Modelo 2 OP tiene solución. 

Es necesario conocer cuales son los costos que las comunidades declararán dados los supuestos que a ella se les asignan.

Teorema 5: Estrategias óptimas cuando las comunidades tienen conocimiento incompleto sobre los costos. Asumiendo que , donde , y los mismos supuestos del Teorema 4, la estrategia óptima de las comunidades es:

esto significa que cada comunidad cuando tiene un conocimiento incompleto de los costos de las otras comunidades, con el mecanismo de asignación del Teorema 4, declararía una disposición a recibir el NIMBY que es mayor que su verdadero costo. Es importante destacar que la sobredeclaración depende de las distribuciones que la comunidad supone para cada una de las comunidades restantes, o que es lo mismo, de las creencias que ella tiene sobre las comunidades restantes.

Dem: Para cada comunidad el problema de maximización es:

Planteando las condiciones de Karush-Kuhn-Tucker tenemos:

Encontrar el equilibrio de Nash, requiere resolver las ecuaciones simultaneas de mejor respuesta de cada comunidad. La función es negativa, por tanto el máximo se alcanza cuando , ya que el caso negativo estricto condiciona alcanzar el extremo del intervalo (despejar de (24)(ia)), y ello ocurre en algún valor de .

Para obtener una expresión aproximada del valor óptimo del costo declarado , dado que la ecuación es no lineal, entonces podemos aproximar la solución mediante las expresiones de Taylor:

Reemplazando (25) en , se tiene

de donde se despeja una ecuación cuadrática de .

Luego la solución de (26) que es una solución aproximada del costo declarado óptimo, tenemos que .

Es decir, la declaración de disposiciones a recibir el NIMBY mantiene la relación de orden con los verdaderos costos.

 

3. CONCLUSIONES

En este artículo propusimos un mecanismo de asignación de NIMBY con compensaciones para comunidades con neutralidad al riesgo. Hallamos que cuando las comunidades desconocen completamente los costos del resto, la estrategia óptima es declarar sus verdaderos costos, con lo que el mecanismo resuelve perfectamente el problema de eficiencia, aumentando el bienestar de todas las comunidades, excepto la hospedadora, que lo mantiene.

Cuando las comunidades tienen conocimiento incompleto del costo del resto de las comunidades, el mecanismo no induce a la revelación de los verdaderos costos, habiendo sobredeclaraciones sistemáticas, pero los costos declarados resultan proporcionales a los verdaderos costos. En tal caso, también el mecanismo de asignación es eficiente, además, todas las comunidades aumentan su bienestar.

 

4. TRABAJOS FUTUROS

Sin duda que este trabajo es sólo un eslabón más para la comprensión y aplicación del problema de localización de NIMBY. La posibilidad de implementar un mecanismo como el propuesto, para verificar la robustez a funciones de utilidad más generalizables, a distintos grados de aversión al riesgo, y de distintas soluciones tecnológicas para los NIMBY, incluyendo su división, son desarrollos más promisorios a partir de los resultados que hemos derivado en este trabajo.

 

5. AGRADECIMIENTOS

Agradecemos los comentarios de Sigifredo Laengle, Vladimir Marianov, Jorge Vera, a los dos jurados anónimos de la Revista y el financiamiento del proyecto Fondecyt, 1050670. Las disculpas usuales se aplican.

 

REFERENCIAS

[1] COURSEY, D AND KIM, S. An Examination of compensation Mechanisms to Solve the NIMBY Problem, Working Paper Series: 97.5, The Harris School, University of Chicago, 1997. http://harrisschool.uchicago.edu/About/publications/working-papers/abstract.asp?paper_no=97%2E05 [citado Diciembre 2008] .         [ Links ]
[2] Pew Center On Global Climate Change, http://www.pewclimate.org/ [Revisado Diciembre 2008] .         [ Links ]
[3] HEIMAN, M. Waste Management and Risk Assessment: Environmental Discrimination through Regulation, Special Issue of Urban Geography, December 19, 1999, http://www.ejnet.org/ej/wmra.html [citado Diciembre 2008] .         [ Links ]
[4] “Kennedy faces fight on Cape Wind, Key lawmakers oppose his bid to block project”, Disponible en: http://www.boston.com/news/nation/washington/articles/2006/04/27/kennedy_faces_fight_on_cape_wind/ [citado Diciembre 2008] .         [ Links ]
[5] FREY, B. S., OBERHOLZER-GEE, F. AND EICHENBERGER, R. The Old Lady Visits Your Backyard: A Tale of Morals and Markets, The Journal of Political Economy, Vol. 104, Nº 6, 1297-1313, 1996.         [ Links ]
[6] GERRARD, M., Whose Backyard, Whose Risk: Fear and Fairness in Toxic and Nuclear Waste Siting, The MIT Press, Cambridge, 1994.         [ Links ]
[7] KUNREUTHER, H. AND EASTERLING, D. The Role of Compensation in Sitting Hazardous Facilities, Journal of Policy Analysis and Management, Vol. 15, No. 4, 601-622,1996.         [ Links ]
[8] KUNREUTHER, H., LINNEROOTH-BAYER, J. AND FITZGERALD, K. Sitting Hazardous Facilities: Lessons from Europe and America, Risk Management and Decision Processes Center working paper, 96-08-22, 1996. Disponible en: http://opim.wharton.upenn.edu/risk/downloads/archive/arch101.pdf . [citado Diciembre 2008]         [ Links ]
[9] MITCHELL, R. C. AND CARSON, R. T. Property Rights, Protest, and the Sitting of Hazardous Waste Facilities, The American Economic Review, Papers and Proceedings of the Ninety-Eighth Annual. Meeting of the American Economic Association, Vol. 76, Nº 2, 285-290, 1986.         [ Links ]
[10] BALIGA, S. AND MASKIN, E. Mechanism Design for the Environment. In K.G. Mäler, and J. Vincent (eds.), Handbook of Environmental Economics, Elsevier Science/North Holland, 1, pp.306-324, 2003.         [ Links ]
[11] D’ASPREMONT, C., CRÉMER, J. AND GÉRARD-VARET, L.-A. Incentives and the Existence of Pareto-Optimal Revelation Mechanism, Journal of Economic Theory, 51, 233-254, 1990.         [ Links ]
[12] GREEN, J. AND LAFFONT, J.-J. Characterization of Satisfactory Mechanisms for the Revelation of Preferences for Public Goods, Econometrica, 45 , Nº 2, 427-438, March 1977.         [ Links ]
[13] HURWICZ, L. The Design of Mechanisms for Resource Allocation, The American Economic Review, Papers and Proceedings of the Eighty-fifth Annual Meeting of the American Economic Association, Vol. 63, No. 2, 1-30, 1973.         [ Links ]
[14] GREEN, J. AND LAFFONT, J.-J. On the Revelation of Preference for Public Goods, Journal of Public Economics, Vol. 8, Nº 1, 79-83, 1977.         [ Links ]
[15] D’ASPREMONT, C. AND GÉRARD-VARET, L.-A. Incentives and Incomplete Information, Journal of Public Economics, 11, 25-45, 1979.         [ Links ]
[16] GROVES, T. Incentives in Teams, Econometrica, Vol. 41, Nº 4, 617-631, 1973.         [ Links ]
[17] GROVES, T. AND LEDYARD, J. Optimal Allocation of Public Goods: A Solution to the ’Free Rider’ Problem, Econometrica, Vol. 45, No. 4, 783-810, 1977.         [ Links ]
[18] KIM, S. An Almost Ideal Solution to the Siting Problem of Publicly Provided Indivisible Goods, International Tax and Public Finance, Vol. 10, Nº 4, 357-375, 2003.         [ Links ]
[19] KUNREUTHER, H AND KLEINDORFER, P. A. Sealed-Bid Auction Mechanism for Sitting Noxious Facilities, The American Economic Review, Papers and Proceedings of the Ninety-Eighth Annual Meeting of the American Economic Association, Vol. 76, No. 2, 295-299, 1986.         [ Links ]
[20] MINEHART, D. AND NEEMAN, Z. Effective Siting of Waste Treatment Facilities, Journal of Environmental Economics and Management, 43, 303-324, 2002.         [ Links ]
[21] SULLIVAN, A. Sitting noxious facilities: A sitting lottery with victim compensation, Journal of Urban Economics, Vol. 31, Issue 3, 360-374, 1992.         [ Links ]
[22] O’ SULLIVAN, A. Voluntary Auctions for Noxious Facilities: Incentives to Participate and the Efficiency of Sitting Decisions, Journal of Environmental Economics and Management, Vol. 25, Issue 1, pp. S12-S26, 1993.         [ Links ]
[23] JEAN-MARIE, A., MARCHETTI, N. AND TIDBALL, M. Low-bid Auction Versus High-bid Auction For Sitting Noxious Facilities in a Two-city Region: an Exact Approach, CIRANO Scientific Publications, 2004s-52, http://www.cirano.qc.ca/en/, 2004, [citado Diciembre 2008] .         [ Links ]
[24] CRESPO. F. AND PAREDES, R. Localización de NIMBY mediante subasta tipo Vickrey como un problema de asignación cuadrática, Memorias XIV Latin Ibero-American Congress on Operations Research (CLAIO 2008) - Book of Extended Abstracts, Septiembre 2008.         [ Links ]
[25] MYERSON, R. AND SATTERTHWAITE, M. Efficient mechanisms for bilateral trading, Journal of Economic Theory, 29, 265–281, 1983.         [ Links ]
[26] BABAIOFF, M. AND WALSH, W. E. Incentive Compatible Supply Chain Auctions, en: Multiagent based Supply Chain Management (Eds. B. Chaib-draa, J. P. Müller), Springer-Verlag Berlin Heidelberg, pp.315-350, 2006.         [ Links ]
[27] HURWICZ, L. AND REITER, S., Designing Economic Mechanisms, Cambridge University Press, New York, 2006.         [ Links ]
[28] BINMORE, K., Teoría de Juegos, McGraw-Hill/Interamericana de España, S. A., Madrid, 1994.         [ Links ]
[29] MANGASARIAN, O., Nonlinear Programming, McGraw-Hill Book, Company, New York, 1969.         [ Links ]
[30] AUBIN, J.-P., Optimal and Equilibria: An Introduction to Nonlinear Analysis, Second edition, Springer-Verlag, Berlin, Heidelberg, 1998.         [ Links ]