Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.77 no.162 Medellín Apr./June 2010
MODELO PRIMITIVO MEJORADO PARA IONES HIDRATADOS CERCA DE UNA SUPERFICIE METÁLICA: SIMULACIONES MONTE CARLO
AN IMPROVED PRIMITIVE MODEL FOR HYDRATED IONS NEAR A METAL SURFACE: MONTE CARLO SIMULATIONS
JUAN CARMONA
Escuela de Procesos y Energía, Universidad Nacional de Colombia, Medellín, Colombia. jccarmon@unal.edu.co
BIBIAN HOYOS
Escuela de Procesos y Energía, Universidad Nacional de Colombia, Medellín, Colombia. bahoyos@unal.edu.co
Recibido para revisar Febrero 5 de 2009, aceptado Abril 3 de 2009, versión final Mayo 17 de 2009
RESUMEN: La estructura de la doble capa eléctrica (EDL) formada por iones solvatados cerca de una superficie metálica fue estudiada mediante simulaciones Monte Carlo usando un modelo primitivo mejorado. El modelo propuesto, que incluye radios y potenciales de adsorción diferentes para las atmósferas solvatantes, se aplicó al sistema interfacial Ni(111)-NiCl2(Acuoso). Los resultados del modelo muestran oscilaciones en los perfiles de densidad y de potencial, así como la separación e inversión de la carga en la EDL. Adicionalmente, el modelo muestra un predominio del efecto de tamaño de los iones sobre el efecto de la asimetría de la carga, produciendo un potencial de carga cero (PZC) positivo para el sistema estudiado, a pesar de que la adsorción de la atmósfera hidratante de los aniones es más favorable que la de los cationes. Estas características estructurales de la EDL son muy diferentes a las encontradas con modelos primitivos más simples, restringidos o no.
PALABRAS CLAVE: Doble Capa eléctrica, Modelos Primitivos, Simulación Monte Carlo, Electroquímica.
ABSTRACT: The structure of the electrical double layer (EDL) formed by solvated ions near a metal surface was studied by Monte Carlo simulations using an improved primitive model. The proposed model, which includes different radius and adsorption potentials for each solvating atmosphere, was applied to the interfacial system Ni(111)-NiCl2 (aqueous). Model results show oscillations in the profiles of density and potential, and the separation and reversal of the charge in the EDL. Additionally, the model shows a prevalence effect of ions size over the asymmetric charge effect, producing a positive potential of zero charge (PZC) for the studied system, although the adsorption of the hydrating atmosphere of anions is more favorable than that of cations. These structural characteristics of the EDL are very different from those found with simple primitive models, restricted or not.
KEYWORDS: Electrical double layer, Primitive models, Monte Carlo simulations, Electrochemistry.
1. INTRODUCCIÓN
La estructura de la doble capa eléctrica (EDL) que se forma cuando dos fases se ponen en contacto es determinante en los fenómenos cinéticos y en las propiedades de equilibrio asociados con esta zona. De esta manera las energías de activación para los procesos de transporte de iones y de transferencia de carga están determinadas en gran medida por la estructura de la EDL [1-2], así como la capacidad de almacenamiento de carga en esta región y su relación con el potencial aplicado. Estos hechos convierten a la EDL en un área de estudio crucial para cualquier campo de aplicación particular de la electroquímica debido a que en la mayoría de los casos los fenómenos controlantes en este tipo de procesos ocurren en la interfase electrodo-electrolito.Estos hechos han derivado en un exhaustivo y continuo intento de profundizar teóricamente en la estructura de la EDL.
La primera forma de hacerlo fue mediante la ecuación de Poisson-Boltzmann (PB) para iones considerados como cargas puntuales, inmersas en un medio con permitividad constante, con distancia de máximo acercamiento (DCA) al electrodo igual a cero (modelo de Gouy-Chapman) y diferente de cero (modelo de Gouy-Chapman-Stern). Sin embargo, estos modelos clásicos, que funcionan bien cerca del potencial de carga cero para electrolitos simétricos monovalentes con concentraciones bajas [3], no dan una descripción completa de los fenómenos de doble capa que aparecen asociados a los diferentes tamaños iónicos, a la polarización interna de las especies, a la solvatación o la estructura superficial del metal. Esto propició la generación de nuevos modelos teóricos (basados principalmente en la ecuación de PB y en la integral de Orstein-Zernike), llamados modelos primitivos (PM), los cuales consideran los iones como esferas duras inmersas en un medio continuo.
Las ecuaciones integro-diferenciales de los acercamientos teóricos se han resuelto con algunas aproximaciones y métodos que se listan en extensas revisiones sobre el tema [4-5] y algunos resultados de capacitancia para los diferentes modelos se encuentran resumidos en una recopilación reciente [6]. Pero esos modelos clásicos, y sus extensiones, aún conservan limitaciones en cuanto a la descripción del solvente: en algunos trabajos se considera el solvente como un continuo [7-11], y en otros, llamados modelos primitivos de solvente (SPM), como esferas neutras duras [12-14] o como dipolos [15-16] sin interacciones de dispersión con los iones y con el metal.
La necesidad de validación y la dificultad que presentan los desarrollos teóricos para incluir características más realistas a los modelos, propiciaron el extensivo desarrollo de simulaciones moleculares de la EDL como una herramienta poderosa aplicable a modelos de diferente complejidad, desde los más simples como los PM hasta los más explícitos [1,17-23] en los cuales se consideran todas las especies, iones y solvente, como entidades discretas e inclusive con distribución de cargas en las moléculas de solvente.
A pesar de las ventajas de los modelos más explícitos, estos presentan un alto costo computacional y aumentan la dificultad de simular electrolitos con baja concentración por requerir cálculos con cantidades prohibitivas de moléculas de solvente. Por esta razón y por el éxito de las primeras simulaciones Monte Carlo [24-25] que emplearon los PM para identificar fenómenos que ocurren en la EDL inaccesibles desde los modelos teóricos [3], los modelos primitivos continúan sirviendo como base para ese tipo de simulaciones [6-9,13-14,26-28].
Por la utilidad de los modelos PM y la influencia de las interacciones de dispersión en las propiedades de las EDL [29], en este trabajo se presenta un modelo primitivo que incluye este tipo de interacciones. En esta propuesta se considera que tanto los cationes como los aniones permanecen siempre solvatados cerca de la superficie del electrodo, de tal manera que cada ión y sus aguas de hidratación presentan interacciones de dispersión con los otros iones y con sus respectivas aguas de hidratación. Adicionalmente, en este modelo se consideran las interacciones de adsorción de las atmósferas hidratantes de cada ión con el electrodo.La suposición de que los iones permanecen hidratados cerca del PZC se basa en resultados de simulaciones del tipo explícitas, en las cuales se encontró que los iones monovalentes permanecen hidratados cerca del electrodo [1]. En el caso de los cationes divalentes se supone, por las fuerzas electrostáticas, que la solvatación es inclusive más fuerte. El modelo propuesto se aplica en la determinación de los perfiles de potencial y de densidad de iones para el sistema Ni(111)- solución de NiCl2, considerando que el níquel es uno de los metales más empleados en los procesos de electro depositación para la formación de nano estructuras [30].
2. MODELO
El modelo de interacciones propuesto para llevar a cabo las simulaciones moleculares consiste en un mejoramiento de los modelos primitivos no restringidos, que consideran los iones solvatados como esferas duras sin interacciones Van der Waals entre ellas y sin interacciones de corto alcance con la pared metálica. A diferencia de los anteriores, el modelo propuesto en esta investigación sí considera interacciones de dispersión entre los iones solvatados e interacciones de adsorción de la atmósfera solvatante de cada ión con la pared metálica.
2.1. Interacciones ión solvatado - ión solvatado
El modelo propuesto representa cada ión como su correspondiente carga embebida por dos esferas blandas concéntricas: la esfera interna (el núcleo) representa la nube electrónica del ión no solvatado y la externa (la coraza) representa el cubrimiento correspondiente a las aguas de hidratación de cada ión. Estos iones solvatados están inmersos en un medio con permitividad relativa εr.
Sobre cada ión hidratado actúa la fuerza electrostática de largo alcance y cuatro interacciones de corto alcance: dos corresponden a la interacción de los otros núcleos sobre el núcleo del ión y sobre su coraza y las otras dos corresponden a la interacción de la atmósfera de hidratación de los otros iones sobre el núcleo del ión y sobre su coraza (figura 1).

Figura 1. Representación esquemática de las interacciones electrostáticas (q-q), núcleo-núcleo (N-N), núcleo-coraza (N-C), coraza-núcleo (C-N) y coraza-coraza (C-C).
Figure 1. Schematic representation of electrostatic interactions (q-q), nucleus-nucleus (N-N), nucleus-shell (N-C), shell-nucleus (C-N) and shell-shell (C-C).
Las interacciones electrostáticas y núcleo - núcleo actúan entre los centros de la esfera donde se ubica la carga; las interacciones núcleo - coraza están desplazadas hasta el radio de solvatación del ion que tiene la coraza y las interacciones entre las atmósferas de hidratación (coraza - coraza) están desplazadas hacia la suma de los radios de hidratación de los dos iones.
Para este modelo de iones solvatados el potencial de interacción es:

Las interacciones electrostáticas de largo alcance entre las cargas qi y qj separadas por una distancia rij, están dadas por:

En la cual εr y ε0 son la permitividad relativa del medio y del vacío, respectivamente.
Las interacciones núcleo - núcleo corresponden a potenciales Lennard-Jones (LJ) actuando entre los centros de los núcleos:
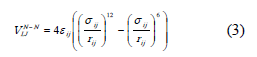
El término debido a las interacciones coraza-coraza es también un potencial LJ actuando entre los radios de hidratación de los iones (rsolv):

Finalmente, los dos términos debidos a las interacciones núcleo - coraza están dadas por:

Los parámetros de los potenciales LJ que representan las interacciones entre los núcleos de los iones (σij, εij), entre el núcleo de un ión y la atmósfera de solvatación del otro (σi-H2O, εi-H2O), y entre las atmósferas de solvatación de los dos iones (σH2O-H2O, εH2O-H2O), se tomaron de la simulación de soluciones acuosas de NiCl2 en la que se consideraron a los iones y al agua como moléculas discretas [31]. Estos parámetros, con σi-H2O, εi-H2O obtenidos mediante las reglas de Lorentz-Berthelot, se muestran en la tabla 1.
Tabla 1. Parámetros de los potenciales Lennard-Jones empleados en el modelo [31].
Table 1. Lenard-Jonnes potential parameters used in the model [31].

2.2. Interacciones ión solvatado - pared metálica
El metal se modela como una superficie lisa que interacciona mediante dos contribuciones con las esferas que representan los iones solvatados: las fuerzas electrostáticas imagen asociadas a las cargas de los iones y las fuerzas de adsorción asociadas a las corazas. Para el cálculo de las primeras, el metal actúa como un espejo a través del cual existe una carga artificiosa de igual magnitud y signo contrario asociada a cada carga real localizada en los centros de los iones en la solución.
Para calcular las interacciones de adsorción de las atmósferas solvatantes con la pared, se usaron potenciales LJ desplazados hasta los radios de solvatación y con parámetros propios para cada ión. Estos potenciales, que dependen de la distancia zi de los iones al metal, fueron ajustados mediante un experimento computacional que se describe más adelante y tienen la forma:

3. DETALLES DE SIMULACIÓN
3.1 Clusters de agua cerca de la pared metálica
Además de las fuerzas imagen, para las interacciones de los iones solvatados con la pared se tiene en cuenta el potencial de adsorción de la atmósfera hidratante de cada ión. Para cada ión, el potencial de adsorción de su atmósfera solvatante sobre la pared, se construye mediante el siguiente experimento computacional: se forma un cluster de seis moléculas de agua localizadas simétricamente en la superficie de una esfera, con radio igual al de solvatación de cada ión y se calcula su energía conforme cambia la distancia del cluster a la pared.
Las moléculas de cada cluster de agua se localizaron, cada una, con su oxígeno en los centros de las seis paredes del cubo que circunscribe a la esfera del ion y con los hidrógenos apuntado hacia dentro del cubo para el cluster correspondiente al Cl-, y apuntando hacia afuera para el Ni+2. Cada cubo se orientó con sus paredes paralelas a los planos coordenados.
El metal consistió de tres capas de 13x14 átomos cada una, paralelas al plano x-y, localizadas en z=-(p-1)*a/√3 con p = 1, 2, 3 (numero de capas de átomos de la pared) y a=3.52Å (parámetro de red del níquel). La disposición de los átomos en las capas de la pared reprodujo una estructura de níquel fcc con orientación (111) en la superficie.
Cada cluster de agua se movió en la región positiva del eje z, con su centro localizado sobre un átomo de la capa superficial del metal. Para calcular la energía entre el cluster de agua y los átomos del metal se usaron condiciones periódicas en x-y, simulando una superficie infinita. Los perfiles se obtuvieron sumando las contribuciones de cada una de las seis moléculas de agua a la energía total, calculadas con un potencial tipo Stilliger-Weber (SW) desarrollado para simulaciones de adsorción de agua sobre diferentes metales, incluido el níquel [32].

Aquí rij es la distancia entre el oxígeno de una molécula de agua i y un átomo metálico j, y φi j es el ángulo entre el vector dipolar de la molécula i y el vector rij. Las letras mayúsculas y los superíndices indican parámetros ajustables que se tomaron, así como las funciones f2 y Φ, de [32].
Finalmente, se ajustaron los parámetros de un potencial tipo LJ (ecuación 7) de tal manera que se reprodujera la energía de adsorción calculada con el método SW. Los potenciales LJ ajustados fueron los usados posteriormente en las simulaciones de la doble capa debido a la simplicidad de su estructura matemática y a la mayor facilidad de incluirlos posteriormente en modelos teóricos.
3.2 Iones solvatados de NiCl2 en medio de dos paredes metálicas
Las simulaciones MC se realizaron posteriormente en ensambles NVT. El número de iones N=N+2+N- se determinó de modo que la concentración en el seno de la solución fuera de 68 mM (N+2=36 y N-=2N+2, para cero carga sobre el metal). El volumen de la caja fue V=WxWxL con el ancho de caja W=31.6Å (10σH2O) y la longitud L=88.5Å (28σH2O). El sistema de iones se confinó entre dos paredes metálicas localizadas en z=0Å y z=88.5Å que interaccionan con los iones mediante los potenciales de adsorción LJ ajustados con la ecuación (7) y mediante las fuerzas electrostáticas de las cargas imagen. Se emplearon condiciones periódicas en 2D con el método de la mínima imagen para las interacciones de corto alcance (LJ) y, para el cálculo de las interacciones electrostáticas, se implementó el método de sumas de Ewald 2D [33], con los iones inmersos en un medio con permitividad relativa igual a la del agua en condiciones estándar (εr = 78.5).
Para simular el exceso de cargas sobre el metal se usó el método de desigualar el número de las cargas positivas y negativas en la solución (N-≠2N+2), lo cual induce, por fuerzas imagen, una carga de igual magnitud y signo contrario sobre la superficie del metal. Para simular los excesos positivos de carga en el metal se adicionaron 4, 8, 12 y 16 iones Cl- a la cantidad inicial N-=72. Los excesos negativos en el metal se simularon con la adición de 2, 4, 6 y 8 iones Ni+2.
Para todas las simulaciones se realizaron 3x106 ciclos de equilibración e igual número de ciclos de producción, partiendo de una configuración inicial previamente equilibrada. Todas las simulaciones se realizaron a 298K.
4. RESULTADOS
4.1 Potenciales LJ para clusters de agua cerca de la pared metálica
Los resultados del ajuste del potencial LJ a los cálculos SW, empleados posteriormente como potenciales de adsorción de los iones solvatados sobre la pared, se presentan en la Fig. 2 y en la Tabla 2. En esta figura, con la superficie metálica localizada en el origen del eje z, los símbolos sólidos corresponden a los potenciales de adsorción calculados usando SW para los clusters asociados a las atmósferas de solvatación de Ni+2 y Cl-, respectivamente. Las líneas corresponden a los potenciales tipo LJ que se ajustaron a los resultados SW. Puede observarse que en la mayor parte de las curvas estos ajustes son buenos en cuanto a forma y magnitud, con unas pequeñas desviaciones cerca de los puntos de inflexión (mayor en valor absoluto para el Cl-) que se consideran poco influyentes debido a que estas zonas son de menor probabilidad de localización de los iones en comparación con la zona del pozo energético.

Figura 2. Resultados del ajuste de parámetros del potencial LJ para las interacciones agua de hidratación- pared. Se grafica la energía de cada cluster en unidades reducidas E/εH2O-H2O
Figure 2. Results of the adjustment of LJ potential parameters for hydration water-wall interactions. Cluster energy is plotted in reduced units E/εH2O-H2O
Tabla 2. Parámetros de los potenciales LJ ajustados a los resultados del potencial SW.
Table 2. LJ potential parameters adjusted to the SW potential results

La diferencia en la localización de los mínimos de potencial se debe a los diferentes radios de solvatación considerados para cada ión, y la diferencia en las magnitudes de estos mínimos se debe a que una molécula de agua cuyo vector dipolar apunta hacia afuera de la superficie (hacia el centro del ión Cl-) se adsorbe más fácilmente que una en la que el vector apunta hacia adentro de la superficie (hacia afuera del ión Ni+2). Esto hace que la capa de solvatación del Cl- se adsorba más fuertemente que la del Ni+2, pero con una distancia de máximo acercamiento también mayor, lo cual influirá en la forma de los perfiles de densidad y en el signo del PZC.
4.2 Simulaciones MC de iones solvatados de NiCl2 en medio de dos paredes metálicas
Mediante las simulaciones MC se obtuvieron los perfiles de distribución axial gi(z) de las especies Ni+2 y Cl-. Con estos perfiles se puede calcular el potencial interfacial ψ(z) mediante (9), el cual representa la diferencia de potencial eléctrico entre un plano ubicado en z y el seno de la solución, donde el potencial es homogéneo y se le asigna el valor de cero.
 (9)
(9)
En la ecuación (9) qi representa la carga de cada ión y ρi es el número de iones por unidad de volumen en el seno de la solución, el cual se ubica en L/2 para el caso práctico del sistema con volumen W2xL.
Debido a que los perfiles de distribución axial y de potencial son simétricos respecto al centro de la caja de simulación, solo se presentaran los resultados correspondientes a la región z<L/2.
Como el potencial SW fue desarrollado para moléculas de agua en equilibrio con un metal y con otras moléculas circundantes, incluidas las del seno, los potenciales ajustados para las interacciones entre la pared y las atmósferas solvatantes presentan un grado de sobre estimación de la adsorción. Esto se debe a que en los experimentos computacionales no fueron consideradas moléculas de agua adicionales a las seis de cada cluster. Sin embargo, como esto ocurre tanto para la atmósfera del catión como para la del anión, las cantidades relativas de estos cerca del metal, y por tanto los perfiles de potencial, deben estar poco afectados por esa restricción.
En la Figura 3 se observan los perfiles de distribución axial y de potencial para el PZC. Se puede ver que se produce una primera capa de iones níquel adsorbidos sobre el metal (debido principalmente a su menor tamaño), seguida por una capa de iones Cl- que sobre balancea a la primera capa (como se puede apreciar en la reversión de la carga mostrada en la figura 3b). Este sobre balance de las cargas positivas puede deberse a tres factores: la asimetría de valencia entre los iones, que ha sido identificada como causante del sobre apantallamiento mediante simulaciones MC [26,34]; la consideración de diferentes tamaños reportada con modelos teóricos [35]; y, finalmente, a que el potencial de adsorción del Cl- es más negativo que el del Ni+2. De la Figura 3 se puede inferir el elevado campo eléctrico que se genera cerca de la superficie por la reversión de la carga.

Figura 3. Perfiles de distribución axial (a) y potencial interfacial (b), con σM = 0 mC/m2 (condición de PZC)
Figure 3. Axial distribution profile (a) and interfacial potential (b), with σM = 0mC/m2 (PZC condition).
El balance en exceso de la segunda capa debe ser compensado por dos capas difusas adicionales de Ni+2 y Cl-, respectivamente. Lo cual produce oscilaciones en los perfiles de carga y potencial. En este último se pueden identificar tres regiones: las dos primeras corresponden a perfiles lineales debidos a la localización fija de la primera y segunda capa, y una tercera región curva y oscilante correspondiente a las capas difusas. La primera región lineal es un potencial constante debido a que la carga neta en la EDL es justamente cero.

Figura 4. Perfiles de distribución axial (a) y potencial interfacial (b), con σM = +64.4mC/m2.
Figure 4. Axial distribution profiles (a) and interfacial potential (b), with σM = +64.4 mC/m2.
Diferentes estudios para modelos primitivos sin adsorción han mostrado que el signo del PZC depende de la influencia relativa de dos efectos contrapuestos: la asimetría en la valencia y la diferencia de tamaño entre los iones [34]. Para electrolitos 2:1, el primer efecto tiende a generar un PZC negativo mientras que el menor tamaño del catión lo conduce hacia la región positiva [24-25].
Para el caso del electrolito considerado en esta investigación, los modelos primitivos que no consideran la adsorción de la atmósfera hidratante producen un PZC negativo [34] mostrando predominio del efecto de la asimetría de la valencia. Por el contrario, el modelo presentado aquí predice un incremento de la concentración de ambos iones en la zona cercana a la superficie con predominio del efecto del tamaño (lo cual genera un PZC positivo).

Figura 5. Perfiles de distribución axial (a) y potencial interfacial (b), con σM = -64.4mC/m2.
Figure 5. Axial distribution profiles (a) and interfacial potential (b), with σM = -64.4 mC/m2.
Al aplicar una carga al electrodo, las simulaciones MC realizadas por otros autores, reportan que la especie predominante en la primera capa es el contra-ión [24-26]. Sin embargo, los resultados de esta investigación, al incluir los potenciales de adsorción de la atmósfera solvatante, muestran que la primera capa de iones siempre es de Ni+2 (inclusive cuando se aplica una carga positiva al electrodo), produciendo perfiles de distribución de iones cualitativamente similares al encontrado para el PZC (Figuras 4 y 5). Para los casos en que se aplica una densidad de carga al electrodo de 64.4mC/m2, tanto positiva como negativa.
(figuras 4 y 5, respectivamente), se presentan diferencias cuantitativas en la concentración de iones en las diferentes capas: cuando la carga es positiva (figura 4), aumenta la concentración de iones de cloro y disminuye la concentración de iones de níquel. Cuando la carga sobre el electrodo es negativa (figura 5), ocurre el efecto contrario.
En todos los perfiles de potencial se observa un domo en la zona positiva, producido por la segunda capa de contra-iones, la cual se generada en todos los casos por el sobre balance, ya discutido, que siempre ocurre con la primera capa. La principal discrepancia entre las Figuras 4 y 5 es la diferencia entre los signos de las pendientes de la primera zona lineal de los perfiles potencial, que corresponden a la diferencia de polaridad entre la carga aplicada en la superficie y la primera capa de iones que siempre es de Ni+2. Estos perfiles pronunciados de potencial tienen un importante efecto en la transferencia de iones a través de la EDL y en la velocidad de reacción de éstos sobre el metal [1-2].
Al duplicar las densidades de carga sobre el electrodo (los datos no se muestran), los resultados obtenidos son similares a los discutidos, solamente que tanto los perfiles de distribución como de potencial se desplazan en la dirección respectiva del signo de la carga aplicada. Estudios recientes de la estructura de la EDL para el caso en el que se aplica una carga positiva en el metal en condiciones similares a las estudiadas en esta investigación (electrolito 2:1, ~10-2M, ~10-2C/m2), y los cuales consideran iones solvatados con igual tamaño del anión y del catión y no incluyen los potenciales de adsorción, reportan perfiles de distribución monótonos [9,36], diferente a los resultados discutidos en párrafos anteriores, en los que se observan inversiones de carga y potencial. En otra investigación reciente, para condiciones iguales a las anteriores pero con mayor concentración de electrolito (1M), se obtienen perfiles de distribución oscilantes [26]. Sin embargo, no se observa la separación entre las dos primeras capas de iones, sino que se presentan distribuciones con un solo domo relativamente amplio para el co-ión.
5. CONCLUSIONES
La inclusión del fenómeno de adsorción de la atmósfera solvatante en modelos primitivos para la descripción de la EDL de electrolitos 2:1, muestra la modificación de la importancia relativa del efecto de la asimetría en la carga y del tamaño de los iones en el signo del PZC. En el caso del sistema Ni(111)- solución de NiCl2, esta inclusión predice un predominio del efecto de tamaño, produciendo un PZC positivo. Además, produce una similitud cualitativa entre los perfiles de distribución iónica correspondientes a las diferentes densidades de carga aplicada en el electrodo.
La consideración de diferentes tamaños iónicos y de potenciales de adsorción en modelos primitivos para simular la estructura de las EDL con iones solvatados, revela características como la separación e inversión de carga, el sobre apantallamiento y las oscilaciones del potencial que no son identificables, son subestimadas e inclusive opuestas a las encontradas con modelos más simples. La combinación de esos dos factores produce un cambio abrupto de potencial (de positivo a negativo) cerca de la superficie metálica, lo cual puede tener una gran influencia en la cinética de electrodepositación de níquel debido al campo eléctrico generado en la zona de reacción.
Estos resultados pueden servir de base para una futura validación de modelos teóricos para iones solvatados que incluyan potenciales tipo LJ. Asimismo, el modelo presentado es fácilmente transferible a electrolitos con valencias y tamaños diferentes, siempre que se quiera incluir la solvatación de los iones y la naturaleza metálica de la pared sólida.
Este modelo puede combinarse con los que consideran el cambio de la permitividad del medio en las diferentes regiones de los sistemas electrodo-electrolito para obtener simulaciones más realistas.
AGRADECIMIENTOS
Este trabajo se pudo llevar a cabo gracias a la financiación de la Vicerrectoría de investigación (código del proyecto: 308051015) y de la Dirección de investigación de la sede Medellín (DIME) (código: 050501004) de la Universidad Nacional de Colombia y al apoyo de la Unidad de Calculo Numérico Avanzado (UNICA).
REFERENCIAS
[1] SPOHR, E., Molecular dynamics simulations of water and ion dynamics in the electrochemical double layer, Solid State Ionics, 150, 1-12, 2002. [ Links ]
[2] ZHDANOV, V. P. AND KASEMO, B., Role of the field fluctuations in electrochemical reactions, Surf. Sci., 521, L655-L661, 2002. [ Links ]
[3] TORRIE, G. M. AND VALLEAU, J. P., Electrical double layers. 4. Limitations of the Gouy-Chapman theory, J. Phys. Chem., 86, 3251-3257, 1982. [ Links ]
[4] GUIDELLI, R. AND SCHMICKLER, W., Recent developments in models for the interface between a metal and an aqueous solution, Electrochim. Acta, 45, 2317-2338, 2000. [ Links ]
[5] PARSONS, R., Electrical double layer: recent experimental and theoretical developments, Chem. Rev., 90, 813-826, 1990. [ Links ]
[6] VALISKÓ, M., HENDERSON, D. AND BODA, D., The capacitance of the electrical double layer of valence-asymmetric salts at low reduced temperatures, J. Mol. Liq., 131-132, 179-184, 2007. [ Links ]
[7] BHUIYAN, L. B., OUTHWAITE, C. W. AND HENDERSON, D., Some simulation and modified Poisson-Boltzmann theory results for the contact values of an electrolyte near a charged electrode, J. Electroanal. Chem., 607, 54-60, 2007. [ Links ]
[8] BHUIYAN, L. B., OUTHWAITE, C. W. AND HENDERSON, D., Planar electric double layer for a restricted primitive model electrolyte at low temperatures, Langmuir, 22, 10630-10634, 2006. [ Links ]
[9] MARTÍN-MOLINA, A., QUESADA-PÉREZ, M. AND HIDALGO-ÁLVAREZ, R., Electric double layers with electrolyte mixtures: Integral equations theories and simulations, J. Phys. Chem. B, 110, 1326-1331, 2006. [ Links ]
[10] LAMPERSKI, S. AND OUTHWAITE C. W., Exclusion volume term in the inhomogeneous Poisson-Boltzmann theory for high surface charge, Langmuir, 18, 3423-3424, 2002. [ Links ]
[11] FAWCET, W. R. AND SMAGALA, T. G., New developments in the theory of the diffuse double layer, Langmuir, 22, 10635-10642, 2006. [ Links ]
[12] LAMPERSKI, S. AND POSPIESZNY, K., Influence of the discreteness-of-charge effect on the anion adsorbability at the electrode/electrolyte interface. A Monte Carlo simulation analysis, J. Electroanal. Chem., 541, 193-199, 2003. [ Links ]
[13] HENDERSON, D., GILLESPIE, D., NAGY, T. AND BODA, D., Monte Carlo simulation of the electric double layer: dielectric boundaries and the effects of induced charge, Mol. Phys., 103, 2851-2861, 2005. [ Links ]
[14] LAMPERSKI, S. AND ZYDOR, A., Monte Carlo study of the electrode/solvent primitive model electrolyte interface, Electrochim. Acta, 52, 2429-2436, 2007. [ Links ]
[15] BODA, D., CHAN, K. Y. AND HENDERSON, D., Monte Carlo simulation of an ion-dipole mixture as a model of an electrical double layer, J. Chem. Phys., 109, 7362-7371, 1998. [ Links ]
[16] LAMPERSKI, S. AND OUTHWAITE, C.W., A non-primitive model for the electrode/electrolyte interface based on the Percus-Yevick theory. Analysis of the different molecular sizes, ion valences and electrolyte concentrations, J. Electroanal. Chem. 460 (1999) 135-143. [ Links ]
[17] SPOHR, E., Computer simulation of the structure of the electrochemical double layer, J. Electroanal. Chem., 450, 327-334, 1998. [ Links ]
[18] SPOHR, E., Molecular simulation of the electrochemical double layer, Electrochim. Acta, 44, 1697-1705, 1999. [ Links ]
[19] PHILPOTT, M. R., GLOSLI, J. N. AND ZHU, S. B., Molecular dynamics simulation of adsorption in electric double layers, Surf. Sci., 335, 422-431, 1995. [ Links ]
[20] PHILPOTT, M. R. AND GLOSLI, J. N., Molecular dynamics study of interfacial electric fields, Electrochim. Acta, 41, 2145-2158, 1996. [ Links ]
[21] PHILPOTT, M. R. AND GLOSLI, J. N., Electric potential near a charged metal surface in contact with aqueous electrolyte, J. Electroanal. Chem., 409, 65-72, 1996. [ Links ]
[22] DIMITROV, D. I. AND RAEV, N. D., Molecular dynamics simulations of the electrical double layer at the 1 M KCl solution/Hg electrode interface, J. Electroanal. Chem., 486, 1-8, 2000. [ Links ]
[23] DIMITROV, D. I., RAEV, N. D, SEMERDZHIEV, K., Molecular dynamics simulations of the electrical double layer at 1 M potassium halide solution/Hg electrode interfaces, Phys. Chem. Phys., 3, 448-452, 2001. [ Links ]
[24] TORRIE, G. M. AND VALLEAU, J. P., Electrical double layers. I. Monte Carlo study of an uniformly charged surface J. Chem. Phys., 73, 5807-5816, 1980. [ Links ]
[25] TORRIE, G. M., VALLEAU, J. P. AND PATEY, G. N., Electrical double layers. II. Monte Carlo and HNC studies of image effects, J. Chem. Phvs., 76, 4615-4630, 1982. [ Links ]
[26] MADURGA, S., MARTÍN-MOLINA, A., VILASECA, E., MAS, F. AND QUESADA-PÉREZ, M., Effect of the surface charge discretization on electric double layers: A Monte Carlo simulation study, J. Chem. Phvs., 126, 234703, 2007. [ Links ]
[27] VALISKÓ, M., BODA, D. AND GILLESPIE, D., Selective adsorption of ions with different diameter and valence at highly charged interfaces, J. Phys. Chem. C, 111, 15575-15585, 2007. [ Links ]
[28] LAMPERSKI, S. AND OUTHWAITE, C. W., Monte-Carlo simulation of mixed electrolytes next to a plane charged surface, J. Colloid Interface Sci., 328, 458-462, 2008. [ Links ]
[29] WERNERSSON, E. AND KJELLANDER, R., On the effect of image charges and ion-wall dispersion forces on electric double layer interactions, J. Chem. Phvs., 125, 154702, 2006. [ Links ]
[30] MOTI, E., SHARIAT, M. H. AND BAHROLOLOOM, M. E., Electrodeposition of nanocrystalline nickel by using rotating cylindrical electrodes, Mat. Chem. Phys., 111, 469-474, 2008. [ Links ]
[31] CHIALVO, A. A. AND SIMONSON, M., The structure of concentrated NiCl2 aqueous solutions: what is molecular simulation revealing about the neutron scattering methodologies? J. M., Mol. Phys., 100, 2307-2315, 2002. [ Links ]
[32] SIEPMANN, J. I. AND SPRIK, M., Influence of surface topology and electrostatic potential on water/electrode systems, J. Chem. Phys., 102, 511-524, 1995. [ Links ]
[33] GRZYBOWSKI, A., GWÓZDZ, E. AND BRÓDKA, A., Ewald summation of electrostatic interactions in molecular dynamics of a three-dimensional system with periodicity in two directions, Phys. Rew. B, 61, 6706-6712, 2000. [ Links ]
[34] VALISKÓ, M., HENDERSON, D. AND BODA, D., Competition between the effects of asymmetries in ion diameters and charges in an electrical double layer studied by Monte Carlo simulations and theories, J. Phys. Chem. B, 108, 16548-16555, 2004. [ Links ]
[35] JIMÉNEZ-ÁNGELES, F. AND LOZADA-CASSOU, M., A model macroion solution next to a charged wall: overcharging, charge reversal, and charge inversion by macroions, J. Phys. Chem. B, 108, 7286-7296, 2004. [ Links ]
[36] QUESADA-PÉREZ, M., MARTÍN-MOLINA, A. AND HIDALGO-ÁLVAREZ, R., Simulation of electric double layers with multivalent counterions: Ion size effect, J. Chem. Phvs., 121, 8618-8626, 2004. [ Links ]














