Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.77 no.163 Medellín July/Sept. 2010
HOTELLING'S T2 CONTROL CHARTS BASED ON ROBUST ESTIMATORS
CARTAS DE CONTROL T2 DE HOTELLING BASADAS EN ESTIMADORES ROBUSTOS
SERGIO YÁÑEZ
Escuela de Estadística, Universidad Nacional de Colombia, Medellín, Colombia, syanez@unalmed.edu.co
NELFI GONZÁLEZ
Escuela de Estadística, Universidad Nacional de Colombia, Medellín, Colombia, ngonzale@unalmed.edu.co
JOSÉ ALBERTO VARGAS
Departamento de Estadística, Universidad Nacional de Colombia, Bogotá, Colombia, javargasn@unal.edu.co
Received for review February 24th, 2009, accepted June 2th, 2009, final version June, 22th, 2009
ABSTRACT: Under the presence of multivariate outliers, in a Phase I analysis of historical set of data, the T2 control chart based on the usual sample mean vector and sample variance - covariance matrix performs poorly. Several alternative estimators have been proposed. Among them, estimators based on the minimum volume ellipsoid (MVE) and the minimum covariance determinant (MCD) are powerful in detecting a reasonable number of outliers. In this paper we propose a T2 control chart using the biweight S estimators for the location and dispersion parameters when monitoring multivariate individual observations. Simulation studies show that this method outperforms the T2 control chart based on MVE estimators for a small number of observations.
KEYWORDS: Multivariate Control Charts, MVE Estimators, Outliers, S Estimators.RESUMEN: En presencia de outliers multivariados, durante la Fase I de análisis de datos históricos, la carta de control T2 , basada en los estimadores usuales del vector de medias y de la matriz de varianzas - covarianzas, se comporta de manera deficiente. Varias alternativas se han propuesto. Entre otras, estimadores basados en el elipsoide de mínimo volumen (MVE) y en el determinante de minima covarianza (MCD) son potentes para detectar un número razonable de outliers. En este artículo proponemos una carta de control T2 usando los estimadores S biponderados para los parámetros de localización y dispersion cuando se monitorean observaciones multivariadas individuales. Estudios de simulación muestran que este método supera las cartas T2 basadas en los estimadores MVE para un número pequeño de observaciones.
PALABRAS CLAVES: Cartas de Control Multivariadas, Estimadores MVE, Outliers, Estimadores S.
1. INTRODUCTION
Hotelling's T2 control chart is a widely used tool for monitoring simultaneously several related quality characteristics of a process. See for example [1, 2]. Recently, it has been used for monitoring quality profiles [3, 4].
Following the terminology of [5], in the Stage 1 of Phase I, historical data are studied for determining whether the process was in control and to estimate the in-control parameters of the process. Sometimes is not possible to group these data into rational subgroups [6, 7], so charts are based on individual multivariate observations.
In a Phase I analysis of historical data set, the usual estimates of the process parameters are the sample mean vector and the sample variance-covariance matrix. It is well known that these estimators are sensitive to outlying observations. As a result, statistics plotted on T2 control charts, based on these estimators, perform poorly when there are several outliers [7, 8, 9]. Alternative estimation methods have been proposed in the literature. One approach consists of calculating the T2 statistic based on successive differences variance-covariance matrix estimator. See for example, [7, 10, 11]. Though this method is effective in detecting sustained shifts in the mean vector, it fails to detect outliers as is shown in [7, 9]. Another approach uses robust estimators of the process parameters. In [9] is proposed the use of high breakdown estimation methods based on the minimum volume ellipsoid (MVE) estimators of [12] and the minimum covariance determinant (MCD) method of [13]. He showed that a T2 control chart using MVE estimators was the most effective method to detect out of control signals due to several outliers. In a large simulation study, [14] showed that a T2 control chart based on MVE estimators performs better than a chart based on MCD estimators when the number of observations is small, but the opposite occurs when the number of observations increases. In [15] three multivariate control charts are compared: the S chart, the MVE chart and the Usual chart. They did it just for the case p=2 and m=30. In this paper we generalize these results by extending our simulations to several values of p and m. We also extend the types of contamination of parameters. It is our purpose to give conclusions under a more general framework.
2. ROBUST ESTIMATORS
Let  be a set of m observations selected from a p-multivariate normal distribution. The MVE estimator of location and variance-covariance matrix is the pair (t, C) that minimizes the determinant of C, subject to
be a set of m observations selected from a p-multivariate normal distribution. The MVE estimator of location and variance-covariance matrix is the pair (t, C) that minimizes the determinant of C, subject to

where the symbol # means the number of points which satisfies the condition, and is the 0.5-quantil of the chi-square distribution with p degrees of freedom. The values, t and C estimate the center of the smallest ellipsoid containing at least half of the observations and the inverse of the shape matrix of the ellipse, respectively. The cov.mve function of S-PLUS calculates these estimators based on a genetic algorithm.
is the 0.5-quantil of the chi-square distribution with p degrees of freedom. The values, t and C estimate the center of the smallest ellipsoid containing at least half of the observations and the inverse of the shape matrix of the ellipse, respectively. The cov.mve function of S-PLUS calculates these estimators based on a genetic algorithm.
The biweight S estimator of location and shape is defined as the pair (t, C) that minimizes the determinant |k2C|, subject to

where r is Tukey's biweight function. An algorithm proposed by [16] to calculate these estimators is outlined in the Appendix.
MVE and S estimators are good candidates to estimate process parameters because they are affine equivariant and have high breakdown points [16, 17]. The breakdown point is the smallest fraction of contamination that causes an estimator to take on values arbitrarily far away [17]. S estimators properties has been widely studied as a high-efficiency robust estimators. See for example, [16, 18, 19, 20, 21].
3. THE T2 CONTROL CHART
We assume that the data set from Phase I analysis consists of m statistically independent observations xi,  such that xi~Np(m, S), where p represents the number of quality characteristics being monitored. The usual estimators of m and S are
such that xi~Np(m, S), where p represents the number of quality characteristics being monitored. The usual estimators of m and S are

respectively. The T2 statistics based on the usual estimators are

Those based on MVE and S estimators are

respectively.
Upper control limits (UCL) for the three charts were calculated from 5000 simulations with an overall false alarm probability of 0.05. Once control limits were calculated, the  (the . should be replaced by U, MVE, or S) were plotted on the chart.
(the . should be replaced by U, MVE, or S) were plotted on the chart.
4. SIMULATION SCHEMES
Sets of m=30, 40 and 50 observations were generated from multivariate normal distributions. Without loss of generality, we assume that the in-control distribution is multivariate normal with mean m0=0 and covariance matrix S0=I, the identity matrix. Let  denote the non-centrality parameter, which measures the shift from m0 to an out-of-control mean vector m1. To generate outliers that contaminated the in-control distribution, k < m observations were randomly generated as follows:
denote the non-centrality parameter, which measures the shift from m0 to an out-of-control mean vector m1. To generate outliers that contaminated the in-control distribution, k < m observations were randomly generated as follows:
- Shift the mean vector: k observations were generated from Np(m1, S0) distributions, for d2=5, 10, 15, 20, 25, p=2, 3, 5, 10, and k=1, 2, ¼, 7.
- Change in the variance-covariance matrix or symmetric contamination: k observations were generated from Np(m0, lS0) distributions, for l=1.5, 2, 2.5, 3.5, 4.5, 8, 10, 12, 16 , p=2, 3, 5, 10, and k=1, 2,¼, 7
- Crossed contamination: k observations were generated from Np(m1, lS0) distributions, for d2=5, 10, 15, 20, 25, l=1.5, 4.5, 8.5, 12.5, p=2, 3, 5, 10, and k=1, 2, ¼, 7.
To evaluate control chart performance, N=1000 replicates were generated for each combination of the above schemes. The control charts, ,
,  and
and  were then compared by estimating the average proportion of outliers detected (APOD). The APOD is a comparison criterion suggested by [22], which is defined as follows
were then compared by estimating the average proportion of outliers detected (APOD). The APOD is a comparison criterion suggested by [22], which is defined as follows

where  is 1 if
is 1 if  and 0 otherwise, and
and 0 otherwise, and  if
if  . Thus, for example, if a data set of size m has 4 outliers and APOD=0.5, then it is expected, on the long run, that the control chart will detect an average of two outliers.
. Thus, for example, if a data set of size m has 4 outliers and APOD=0.5, then it is expected, on the long run, that the control chart will detect an average of two outliers.
Though the signal probability is the usual criterion for comparing multivariate control charts in Phase I analysis [7, 9], we used the APOD because the expected proportion of the exact number of outliers simultaneously detected seems to be more informative than a signal probability, mainly under the presence of multiple outliers. Moreover, limited simulations, not presented here, showed that plots of APOD and signal probabilities exhibit similar patterns when comparing T2 control charts.
5. RESULTS
Figure 1 shows APODs under shifts in the mean vector for different non-centrality parameters, p=2, m=30, and k=1, 4, 7 respectively. For these values of p and m, upper control limits were 10.5123, 24.9336 and 20.2441 for the Usual, MVE and S methods respectively. The Usual T2 control chart performed poorly except when there was just one outlier. For 2 £ k £ 7, estimated APODs for  control charts were consistently superior to those for
control charts were consistently superior to those for  and Usual charts. For instance, in the presence of k=4 outliers and d2=15, the APODs for the
and Usual charts. For instance, in the presence of k=4 outliers and d2=15, the APODs for the  ,
,  and
and  charts were 0.2515, 0.1835 and 0.0275, respectively.
charts were 0.2515, 0.1835 and 0.0275, respectively.

Figure 1. Average proportion of outliers detected under shifts in the mean vector for p=2, m=30, with k=1, 4 and 7 outliers
Table 1 shows estimated APODs for MVE and S methods for p=3, 5, 10, m=30, 40, 50 and k=2, 4, 7. Similar patterns are observed for  and p=2. Otherwise, MVE and S methods had a similar performance.
and p=2. Otherwise, MVE and S methods had a similar performance.
Table 1. Estimated Average proportions of outliers detected by  and
and  under shifts in the mean vector, for p=3, 5, 10, m=30, 40, 50 with k=2, 4 and 7 outliers and several values of the non-centrality parameter d2
under shifts in the mean vector, for p=3, 5, 10, m=30, 40, 50 with k=2, 4 and 7 outliers and several values of the non-centrality parameter d2


Figure 2 shows estimated APODs under symmetric contamination for different values of l, p=2 and m=30, and k=1, 4, 7 respectively. In the presence of a single outlier  control charts are most powerful, but their estimated APODs are smallest when there are several outliers. For multiple outliers, estimated APODs for
control charts are most powerful, but their estimated APODs are smallest when there are several outliers. For multiple outliers, estimated APODs for  are consistently higher than those for
are consistently higher than those for  control charts.
control charts.

Figure 2. Average proportion of outliers detected under symmetric contamination for p=2, m=30, with k=1, 4 and 7 outliers
Table 2 exhibits estimated APODs under symmetric contamination for and
and  control charts and p=3, 5, 10, m=30, 40, 50 and k=2, 4, and 7. Interestingly, estimated APODs increased with p. For instance, for m=50, k=4, and l=8 APODs for the MVE method were 0.433 for p=3, 0.598 for p=5 and 0.794 for p=10. For the S method the values were 0.454, 0.639 and 0.879, respectively. Under this type of contamination the S performs slightly better than the MVE method. Notice that for m=30, regardless of p, estimated APODs for
control charts and p=3, 5, 10, m=30, 40, 50 and k=2, 4, and 7. Interestingly, estimated APODs increased with p. For instance, for m=50, k=4, and l=8 APODs for the MVE method were 0.433 for p=3, 0.598 for p=5 and 0.794 for p=10. For the S method the values were 0.454, 0.639 and 0.879, respectively. Under this type of contamination the S performs slightly better than the MVE method. Notice that for m=30, regardless of p, estimated APODs for  are consistently higher than those for
are consistently higher than those for  control charts.
control charts.
Table 2. Estimated average proportions of outliers detected under symmetric contamination, for p=3, 5, 10, m=30, 40, 50 with k=2, 4 and 7 outliers and several values of l

Under cross contamination, for different combinations of non-centrality parameters and ls, was observed a similar pattern that in Figures 1 and 2 for d2 and l fixed, respectively. Simulation results, not shown here, produce similar results for the combinations of p= 3, 5, 10, m= 30, 40, 50 and k= 2, 4, 7.
6. EXAMPLE
Next we illustrate the comparison of the three types of T2 control charts. We consider the example presented by [23]. The original data set contains 11 quality variables measured on 30 products. Here we consider only the first three variables, whose values are reproduced in the table 3.
Table 3. Variables 1, 2 and 3 of [23] data set
Figure 3 shows the obtained charts. The UCLs for the  ,
,  and
and  charts were 12.275, 30.660, and 25.552, respectively. The Usual and S methods signaled the second observation as out-of-control. In contrast, the MVE method did not.
charts were 12.275, 30.660, and 25.552, respectively. The Usual and S methods signaled the second observation as out-of-control. In contrast, the MVE method did not.
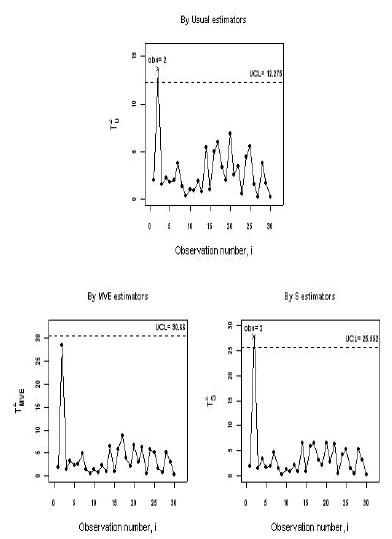
Figure 3. T2 control charts for the first three variables of [23] data set, using Usual, MVE and S estimators
Next, we replaced the 10th and 25th observations by two outlying observations generated artificially, (0.280, 55.640, 21.2) and (0.485, 55.600, 21.7) respectively. Figure 4 presents the three control charts for the modified data set. The Usual method detected only the 10th observation, whereas the MVE method detected the 10th and 25th observations and the S method detected the 2nd, 10th and 25th observations as out-of-control.

Figure 4. T2 control charts for the modified data using Usual, MVE and S estimators
During a Phase I analysis of a historical data set, T2 control charts based on the Usual estimators of the mean vector and covariance matrix of the in-control distribution perform poorly under the occurrence of multiple outliers. We have proposed a T2 control chart that relies on S estimators. Three control charts were compared via simulation: The usual T2 control chart, the T2 control chart with MVE estimators and T2 control chart with S estimators. Our results show that for a small number of observations, control charts with S estimators perform uniformly better than the other two charts. As the number of observations increases, T2 control charts based on S and MVE estimators perform similarly. In any case, under the presence of outliers, robust control charts should be used instead of the Usual T2 control chart.
APPENDIX
Following [16], this appendix describes an algorithm that computes S estimators. S estimators correspond to the global minimum of the objective function using MCD estimators as initial solutions, t(0) and C(0). The intermediate steps of the algorithm are as follows:
(a) Set j=j+1.
(b)Compute
 .
.
(c) Find  as a solution of
as a solution of  , where
, where
 is the Tukey's biweight function.
is the Tukey's biweight function.
(d) Compute  .
.
(e) Set  .
.
(f) Set  ,
,
where

and
 .
.
The constants b0 and c are set such that the breakdown point of S estimators is close to 0.5 [17].
At the end of the iterative process (after j steps, according to some convergence criterion) the pair t(j), C(j) is obtained. Following [24], the following reweighting is done:
(a) Compute  .
.
(b) Compare each  with
with  , where
, where  and
and  are the 0.95 and 0.5 quantiles of a chi-square distribution with p degrees of freedom and
are the 0.95 and 0.5 quantiles of a chi-square distribution with p degrees of freedom and  is the median of the
is the median of the  distances.
distances.
(c) If  then we assign it a weight
then we assign it a weight  . Otherwise,
. Otherwise,  .
.
(e) The final estimators are calculated as

and
 .
.
REFERENCES
[1] LOWRY, C. A, AND MONTGOMERY, D. C. A review of Multivariate Control Charts. IIE Transactions, 27, pp. 800-810, 1995. [ Links ]
[2] MASON, R. L, AND YOUNG, J. C. Multivariate Statistical Process Control with Industrial Applications. SIAM, Philadelphia, P.A, 2002. [ Links ]
[3] KIM, K.; MAHMOUD, M. A, AND WOODALL, W. H. On the Monitoring of Linear Profiles. Journal of Quality Technology, 35, pp. 317-328, 2003. [ Links ]
[4] MAHMOUD, M. A.; AND WOODALL, W. H. Phase I Analysis of Linear Profiles with Calibration Applications. Technometrics, 46 (4), pp. 380-391, 2004. [ Links ]
[5] ALT, F. B, AND SMITH, N. D. Multivariate Process Control. In: Handbook of Statistics, vol. 7, edited by P. R. Krishnaiah and C. R. Rao North-Holland, Amsterdam, pp. 333-351, 1988. [ Links ]
[6] RYAN, T. P. Statistical methods for quality improvement, 2nd ed., John Wiley & Sons, Inc, 2000. [ Links ]
[7] SULLIVAN, J. H.; AND WOODALL, W. H. A Comparison of Multivariate Control Charts for Individual Observations. Journal of Quality Technology, 26, pp. 398-408, 1996 [ Links ]
[8] SULLIVAN, J. H.; AND WOODALL, W. H. Adapting Control Charts for the preliminary Analysis of Multivariate Observations. Communications in Statistics - Simulation and Computation, 27, pp. 953-979, 1998. [ Links ]
[9] VARGAS, J. A. Robust Estimation in Multivariate Control Charts for Individual Observations. Journal of Quality Technology, 35, pp. 367-376, 2003. [ Links ]
[10] HOLMES, D. S.; AND MERGEN, A. E. Improving the Performance of the T2 Control Chart. Quality Engineering, 5, pp. 619-625, 1993. [ Links ]
[11] WILLIAMS, J. D.; WOODALL, W. H.; BIRCH, J. B, AND SULLIVAN, J. H. On the distribution of Hotelling's T2 statistic based on the successive differences covariance matrix estimator. Journal of Quality Technology, 38, pp.217-229, 2006. [ Links ]
[12] ROUSSEEUW, P. J.; AND VAN ZOMEREN, B. C. Unmasking Multivariate Outliers and Leverage Points. Journal of the American Statistical Association, 85, pp. 633-639, 1990. [ Links ]
[13] ROUSSEEUW, P. J.; AND VAN DRIESSEN, K. A fast Algorithm for the Minimum Covariance Determinant Estimator. Technometrics, 41, pp. 212-223, 1999. [ Links ]
[14] JENSEN, W. A.; BIRCH, J. B.; AND WOODALL, W. H. High Breakdown Estimation Methods for Phase I Multivariate Control Charts. Quality and Reliability Engineering International, 23 (5), pp. 615-629, 2007. [ Links ]
[15] YAÑÉZ, S.; VARGAS, J. A. AND GONZÁLEZ, N. Carta T2 con base en estimadores robustos de los parámetros, Revista Colombiana de Estadística, 26(2), pp. 159-179, 2003. [ Links ]
[16] WOODRUFF, D. L.; AND ROCKE, D. M. Computable Robust Estimation on Multivariate Location and Shape in High Dimension Using Compound Estimator. Journal of the American Statistical Association, 89, pp. 888-896, 1994. [ Links ]
[17] ROUSSEEUW, P. J.; AND LEROY, A. M. Robust Regression and Outlier Detection. John Wiley & Sons, Inc, 1987. [ Links ]
[18] DAVIES, P. L. Asymptotic Behaviour of S Estimates of Multivariate Location Parameters and Dispersion Matrices. The Annals of Statistics, 15, pp. 1269-1292, 1987. [ Links ]
[19] LOPUHAÄ, H. P. On the Relation Between S - Estimators and M - Estimators of Multivariate Location and Covariance. The Annals of Statistics, 17, pp. 1662-1683, 1989. [ Links ]
[20] ROCKE, D. M. Robustness Properties of S Estimators of Multivariate Location and Shape in High Dimension. The Annals of Statistics, 24, pp. 1327-1345, 1996. [ Links ]
[21] ROCKE, D. M.; AND WOODRUFF, D. L. Identification of Outliers in Multivariate Data. Journal of the American Statistical Association, 91, pp. 1047-1061, 1996. [ Links ]
[22] KOSINSKI, A. S. A Procedure for the Detection of Multivariate Outliers. Computational Statistics & Data Analysis, 29, pp. 145-161, 1999. [ Links ]
[23] QUESENBERRY, C. P. The Multivariate Short-Run Snapshot Q Chart. Quality Engineering, 13, pp. 679-683, 2001. [ Links ]
[24] MARONNA, R. A.; AND YOHAI, V. J. The Behavior of the Stahel - Donoho Robust Multivariate Estimator. Journal of the American Statistical Association, 90, pp. 330-341, 1995. [ Links ]














