MODEL BASED PREDICTIVE CONTROL OF A ROUGHER FLOTATION CIRCUIT CONSIDERING GRADE ESTIMATION IN INTERMEDIATE CELLS

CONTROL PREDICTIVO DE UN CIRCUITO DE FLOTACIÓN ROUGHER CONSIDERANDO ESTIMACIÓN DE LEYES EN CELDAS INTERMEDIAS

 

DANIEL ROJAS
Electrical Engineering Department, Pontificia Universidad Católica de Chile, dorojas@uc.cl

ALDO CIPRIANO
Electrical Engineering Department, Pontificia Universidad Católica de Chile, PhD, aciprian@ing.uc.cl

 

Received for review February 9^th, 2010, accepted March 14^th, 2010, final version May, 24^th, 2010

 

---

ABSTRACT: Effective control of rougher flotation is important because a small increase in recovery results in a significant economic benefit. Although many flotation control strategies have been proposed and implemented over the years, none of them incorporate concentrate grade measurements at intermediate cells because these data are not usually available. On the other hand, there is much research on characterizing concentrate froth on the cell surface by image processing in order to extract information on froth color, bubble size, and speed that can then be used for developing expert control strategies, and some works have shown the possibility of estimating the concentrate grade. This work presents two multivariable model based predictive control (MPC) strategies for a rougher circuit. The first strategy is based only on general tailings and concentrate grade measurements while the second one includes, beside these data, the intermediate cell grade estimates. Both strategies are compared with a fixed control strategy. Simulation tests show that the recovery can increase by 1.7%, compared to the fixed control strategy.

KEYWORDS: Rougher flotation, grade estimation, dynamic modeling, predictive control.

RESUMEN: En flotación de minerales, pequeños incrementos en la recuperación resultan económicamente muy significativos, por lo que el control automático del proceso ha pasado a ser indispensable. En esta área se han desarrollado varios trabajos en los que usualmente no se consideran leyes de concentrado en celdas intermedias. Por otra parte, se han realizado varios trabajos para caracterizar la espuma de concentrado por medio de procesamiento de imágenes para extraer color, velocidad y tamaño entre otros y unas pocas investigaciones han mostrado la factibilidad de estimar la ley de concentrado. Este trabajo dos estrategias de control predictivo multivariable La primera estrategia está basada sólo en la información entregada por los sensores de cola y concentrado generales mientras que la segunda incluye, además de esta información, estimación de leyes de concentrado en celdas intermedias. Ambas estrategias son comparadas con una estrategia que considera controles fijos. Los resultados por simulación muestran que la recuperación puede ser incrementada hasta en un 1,7% con respecto a la estrategia con controles fijos.

PALABRAS CLAVE: Flotación rougher, Estimación de leyes, modelación dinámica, control predictivo.

---

 

1. INTRODUCTION

Rougher flotation is the first stage in the concentration of low grade minerals and its goal is to maximize recovery, keeping the concentrate grade within acceptable ranges. Good control at this stage is important because it directly affects the performance of the concentrate operation, and small increases of even 0.5% recovery in rougher flotation result in significant economic benefit [8].

Control of the flotation operation is complicated by its non-linear nature, the presence of disturbances, the lack of instrumentation, and other factors that have led to the search for control techniques more advanced than the classic PID, such as expert and predictive control. Regarding instrumentation, existing work falls into two categories: control strategies that use conventional sensors (level, pH, flow, X-ray analyzers) are in the first category, and those based on froth concentrate appearance as detected by visual sensors are in the second category.

On the other hand, systems using image processing have been proposed to capture features such as color, speed, and bubble size [4]. Developed ACEFLOT, a real-time analyzer that determines characteristics of the froth and detects the operation states of each flotation cell by means of a knowledge base [2] reported that froth speed can be used in a supervisory control strategy. Similar work has been done by [1] and [12], achieving significant improvements in zinc concentration plants.

In the first category, various works have been developed. Expert control strategies based on operation zones are proposed and evaluated by simulation in [20] and [15]. The same plant [16] developed a multivariable predictive controller. A global predictive controller consisting of three controllers for a rougher flotation circuit was proposed in [6]. A GPC controller that reduces grade variation was implemented in [19]. A predictive controller using Volterra models was evaluated by simulation [5]. An optimal controller based on dynamic programming was developed in [14], and a hierarchical optimal control strategy was proposed in [17].

Because of the serial structure of the flotation circuit, usually only feed grade, general tailings and concentrate grade are measured on-line, and the concentrate grade in the intermediate cells remains unknown. For that reason the strategies mentioned above use a single pulp level reference for different cells [14].

On the other hand, systems using image processing have been proposed to capture features such as color, speed, and bubble size. ACEFLOT, a real-time analyzer that determines characteristics of the froth and detects the operation states of each flotation cell by mean of a knowledge base, is developed in [4]. In [2] it is reported that froth speed can be used in a supervisory control strategy. Similar work has been done in [1] and [2], achieving significant improvements in zinc concentration plants.

In this field some researchers have succeeded in estimating concentrate grade using image processing. Concentrate grade is predicted by means of image processing and partial least squares regression, with a prediction error of 1.4% in [10]. An empirical model that correlates concentrate grade and froth color using multivariate image analysis MR-MIA is built in [7]. Moreover, in [21] the scores of MR-MIA analysis are used to get a static model of froth concentrate and by means of an inverse model controller that has an input image, it is possible to control the froth appearance. However there is not additional information about the circuit layout and the strategy does not take a dynamic model into consideration; in addition, the performance index is based on the similarity between two images and not on the concentrate grade or recovery.

This paper presents a multivariable model predictive control for rougher flotation, using general tailings and concentrate grade, and an estimation of concentrate grade in intermediate cells, with the aim of achieving high recovery in the presence of different disturbances over time. Control performance is compared with fixed controls and with a model based predictive controller that considers only general tailings and concentrate grade.

 

2. DYNAMIC MODEL OF ROUGHER FLOTATION

There have been numerous developments with flotation models that depend on application and specific purpose. In general, they can be grouped into microscale and macroscale models. Microscale models identify all the subprocesses using chemical and physical relationships, and they are highly complex. Macroscale models can be divided into phenomenological or empirical, dynamic, or static models. Phenomenological models are mass balances that can be kinetic or probabilistic, and they describe particle-bubble behavior. Empirical models are tuned using process data. Static models allow designing plant layouts, but a dynamic model is needed to study control strategies [3].

Flotation can be described with different difficulty levels. Some works consider only a hydraulic model for evaluating regulatory control strategies [11], [13], [18]. Other works incorporate mineral recovery using mass balance equations that may consider pulp and froth phases, or a single mixture. If only one phase is considered, the mathematical complexity is significantly reduced [3], but the model obtained is less precise [5]. We developed a simulator based on the previous work of [9], [14], and [16], based on the following assumptions:

• Constant air flow
• Two mineralogical classes: rich mineral (class i: 1, mainly chalcopyrite) and poor mineral (class i: 2, mainly gangue)
• Each phase in the cell is perfectly mixed.
• Material transfer takes place between phases in both directions, depending on the flotation rate in the pulp and the drainage rate in the froth.
• Array of serial circular cells 2-2-3 (see figure 1)

Figure 1. Rougher flotation circuit diagram

Noise was also added to the measured variables to obtain more realistic results. The equations governing the dynamics of the process are:

Mass balance in froth and pulp phases:

(1)

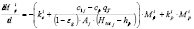(2)

Xa1 is generally known, and the concentration of class 2 is calculated by:

(3)

For the other cells j:

(4)

Concentrate grade in cell j:

(5)

General concentrate grade:

(6)

General tail grade:

(7)

(8)

Where:

Mineralogical class [1, 2]
Cells arrange [1, 2, 3]
Sectional area j
Pulp level j
Total height j
Flotation rate
Drainage rate
Pulp mass
Froth mass
Holdup constant
Heuristic parameters
Feed flow j
Tail flow j
Concentration of mineralogical class in cell j
Concentrate grade in cell j
General concentrate grade
General tail grade
Mineral recovery
Feed mineral grade

Additionally, the flotation and drainage rates depend on collector 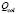and frother .

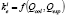
The rougher flotation circuit layout is shown in Figure 1, whose instrumentation considers Courier analyzers for feed, general, and concentrate grade. Additionally, PI level controllers are considered. The manipulated variables are the pulp level references, the measured disturbances are the feed flow, chemical reagents, and feed mineral grade. The sample time considered for the Courier analyzers is 5 minutes. The manipulated variables are the pulp level references in the flotation cells.

Table 1. List of parameters used for simulation

An operation zone for getting a mineral recovery over 80% and a concentrate grade over 15%, which is desirable in a rougher flotation process, is chosen. The steady states values of the dynamic model are listed in Table 2, these points are considered for further linearization of the models used in control strategies.

Table 2. Steady state values of dynamic model

Figure 2 shows how a feed flow increase in minute 50, arising from 17 to 20 [m3/min], causes an increase of the general tail and concentrate grades, therefore decreasing the mineral recovery due to a higher tail grade.

Figure 2. Dynamic response to a feed flow increase

Regarding the noise for measured variables, it corresponds to white noise w(k) with zero mean (E) and variance σ2, satisfying equation 9, which is added to measured disturbances, and tail and concentrate grades.

(9)

 

3. CONTROL STRATEGIES

The aim of control in rougher flotation is to maximize the recovery, keeping the concentrate grade over a minimum. In this paper, three different control strategies are compared from the perspective of their performance and economic benefits. Firstly, we consider a non reactive strategy with a fixed control that does not react to input disturbances. Moreover, we consider two model predictive control strategies, the first one named OPT1, considering general tail and concentrate grades and the other one, named OPT2, considering additional estimation of concentrate grade in intermediate cells.

The MPC strategies presented in this work consider linear models in state space; therefore equations 1, 2, 5, and 6 are linearized around the operating point shown in Table 1. We need to obtain a model representation:

(10)

Where the states input and output vectors for the OPT1 strategy are given by:

Where i = 1, 2 y j = 1, 2, 3. Additionally, according to equations 1 and 2 we define F(x,u):

Considering the general tail and concentrate grades, G(x,u) is defined:

Where are considered as additional parameters in steady state, therefore we calculate A, B, and C matrices:

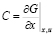
The additional parameters are listed below:

For strategy OPT2, which also takes into account estimations of concentrate grade in intermediate cells, the states, input and output vectors are given by:

Where F(x,u) is kept and G(x,u) is modified to:

With j = 1, 2, 3. The A, B, and C matrices are obtained in a similar way.

Control OPT1 Strategy
Figure 3 describes the OPT1 strategy, where the references for tail and concentrate grade are given by the operator and the MPC algorithm seeks to meet the desired operation conditions by minimizing equation 11: (11)

Where:

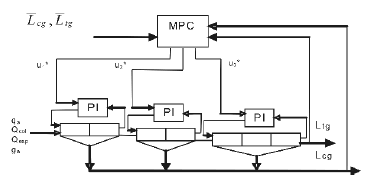
Figure 3. OPT1 control strategy schematic

OPT2 Control Strategy
Figure 4 describes the OPT2 strategy, in which (unlike OPT1) the references are given by intermediate concentrate grade set-points, which are determined by the operator. The cost function is given by equation 11, where:

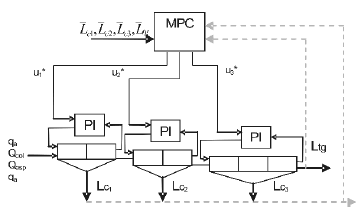
Figure 4. OPT2 control strategy schematic

It is important to mention that the use of linear models may lead to a suboptimal representation of the real process, and hence to suboptimal performance. Nevertheless, the use of linear models is useful for formulating a convex problem of the control law, which ensures a global solution for the optimization problem. This is a practical approach for a real implementation of the strategies presented in this work. Meanwhile, the use of more accurate nonlinear models does not ensure the convexity of the optimization problem.

The results obtained by simulation are shown below.

 

4. SIMULATION RESULTS

Two operating scenarios are simulated, as shown in Figures 5 to 10, and the results obtained with fixed controls, OPT1 and OPT2 strategies are compared. The operating scenarios start from steady state points used for the linearization of models (see Table 2 and 3), which also is considered for assigning the desired set-points for tail and concentrate grades, as shown below.

Table 3. Operational variable values for linearization

Table 4. Reference set-points

For evaluating the performance of control strategies, the mineral recovery and cost function are considered. Therefore, the throughput, concentrate grade, and copper price are merged according to equations 12 and 13:

(12)

(13)

Where

P_Cu: Copper concentrate price (US$3)

Regarding intermediate grade estimations, a sample time of 0.5 min is assumed, which is considered to be the sample time for the OPT2 strategy as well; Meanwhile, the OPT1 strategy considers a sample time of 5 min, according to the references of the layout previously described.

Scenario 1:

An increase in feed flow is simulated in min 50, which rises from 17 to 20 m3/s, as shown in Figure 5. This causes an increase in the grades for the fixed control strategy, as shown in Figure 6 where it can also be seen that OPT1 and OPT2 are able to keep the general tail grade, but with a small increase in the general concentrate grade.

Figure 5. Feed flow increase

Figure 6. Process response

Figure 7 shows how the feed flow affects the intermediate concentrate grades. It can be seen that while grades are increased with the fixed control strategy, the grades are kept with the OPT2 strategy and show a small increase with OPT1 strategy.

Figure 7. Intermediate cell grades for the strategy

Regarding mineral recovery (see Figure 8), this decreases with the fixed controls strategy, which is a not desirable behavior. Meanwhile, the OPT1 and OPT2 strategies are able to keep the desired concentrate grade. However, the OPT2 strategy shows a minor oscillation.

Figure 8. Calculated recoveries

Figure 9 shows the benefits obtained with the OPT1 and OPT2 strategies in comparison with the fixed control strategy. It is shown that OPT1 and OPT2 get benefits and it can be seen how the benefits obtained with OPT2 are greater than OPT1 in transient response. The results are comprised in Table 5.

Figure 9. Profit obtained with regard to the fixed control strategy

Table 5. Comparison of results

Scenario 2:

A feed flow increase at min 50 and a decrease in mineral feed grade at min 150 is simulated, as shown in Figure 10. The feed flow increase (17 to 20 m3/s) causes an increase in the general tail and concentrate grade and after a decrease in the mineral feed grade (1.2 to 0.8%) causes a decrease in the grades as shown in Figure 11, where it can be seen that the OPT1 and OPT2 strategies are able to keep the tail grade near the target and with a small oscillation in general concentrate grade.

Figure 10. Feed flow increase and feed grade decrease

Figure 11. Process response

Figure 12 shows the effect on the concentrate grade in intermediate cells, getting an oscillation with the fixed control strategy. Meanwhile, the OPT1 and OPT2 strategies are able to keep the grades near the target.

Figure 12. Intermediate cell grades for the control strategy

In Figure 13 it can be seen that mineral recovery with fixed controls decreases with the increasing feed flow, and is even lower with the decreasing feed mineral grade. This effect is also appreciated with the OPT1 and OPT2 strategies, which try to keep the general concentrate grade while decreasing the mineral recovery.

Figure 13. Calculated recoveries

Finally, Figure 14 shows how the OPT1 and OPT2 strategies obtain economic benefits over the fixed control strategy, and OPT2 is the strategy with the highest benefits along the simulation.

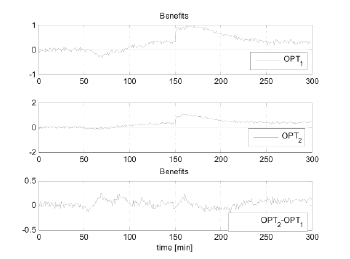
Figure 14. Profit obtained with regard to the fixed control strategy

Table 5 shows a summary of the performance obtained with every strategy in the simulated scenarios. We appreciate the fact that mineral recovery obtained with the OPT1 and OPT2 strategies are similar. Meanwhile, the economic benefits obtained with OPT2 are greater. This is because the benefits are obtained in a transient state, which shows that if a control strategy considers the estimations of concentrate grade in intermediate cells, it is possible to achieve a more stable concentrate grade and mineral recovery.

It is important to mention that the results obtained in this work are only valid within an operation zone, because the MPC algorithm takes linear models into consideration.

 

5. CONCUSIONS AND FUTURE WORK

This work shows that the model based predictive control strategies OPT1 and OPT2 are able to maintain higher performance in the presence of disturbances in the process, getting a 1.7% higher recovery than a process with fixed control. Also, we show that the OPT1 and OPT2 strategies get a similar calculated mineral recovery in a steady state, but the economical benefits considering the transient response are higher with the OPT2 strategy. This suggests that if it were possible to get reliable concentrate grade estimations in intermediate cells, then it would be possible to enhance the process performance in comparison with a model based predictive control strategy that considers only general tailing and concentrate grade and a fixed control strategy.

The next stage in this research ought to consider the development end evaluation of algorithms for concentrate grade estimations.

 

6. ACKNOWLEDGEMENTS

Daniel Rojas acknowledges Conicyt for financing his PhD studies.

 

REFERENCES

[1] BARTOLACCI, G., PELLETIER, P. TESSIER, J., DUSCHESNE C., BOSSÉ, P., FOURNIER, J. "Application of numerical image analysis to process diagnosis and physical parameter measurement in mineral process - Part I: Flotation control based on froth textural characteristics". Minerals Engineering 19 (2006) 734-747.         [ Links ]
[2] BROWN, N., BOURKE, P., RONKAINEN, S., VAN OLST, M. "Improving flotation plant performance at Cadia by controlling and optimizing the rate of recovery using Outokumpu FrothMasterTM". Proceedings of the 33rd Annual Meeting of Canadian Mineral Processors, CIM, Ottawa, Canada (2001) 25-36.         [ Links ]
[3] CASALI, A., GONZÁLEZ, G., AGUSTO, H., VALLEBUONA, G. "Dynamic simulator of a rougher flotation circuit for a copper sulphide ore. Minerals Engineering 15(4) (2002) 253-262"         [ Links ]
[4] CIPRIANO, A., GUARINI, M., VIDAL, R., SOTO, A., SEPÚLVEDA, C., MERY, D., BRICEÑO, H. "A real tine visual sensor for supervision of flotation cells". Minerals Engineering 11(6) (1998) 489-499.         [ Links ]
[5] DELPORT, R. "Process identification using second order Volterra models for nonlinear model predictive control design of flotation circuits". M. Sc. Thesis, Department of Chemical Engineering, University of Pretoria, 2005.         [ Links ]
[6] DESBIENS, A., HODOUIN, D., MAILLOUX, M. "Nonlinear model predictive control of a rougher flotation unit using local models". Proceedings of IFAC Symposium on Automation in Mining, Metal and Mineral Processing, Cologne, Germany (1998) 297-302.         [ Links ]
[7] DUCHESNE, C., BOUAJILA, A., BARTOLACCI, G., PELLETIER, P., BREAU, Y., FOURNIER, J., GIRARD, D. "Application of multivariate image analysis (MIA) to predict concentrate grade in froth flotation processes". Proceedings of the 35th Annual Meeting of the Canadian Mineral Processors, CIM, Ottawa, Canada (2003) 511-526.         [ Links ]
[8] FERREIRA, J. P., LOVEDAY, B. K. "An improved model for simulation of flotation circuits". Minerals Engineering 13(14-15) (2000) 1441-1453.         [ Links ]
[9] HARRIS, CC. "Multiphase models of flotation machines behavior". International Journal of Mineral Process 5(1) (1978) 107-117.         [ Links ]
[10] HATONEN, J., HYOTYNIEMI, H., MIETTUNEN, J., CARLSSOM, L. "Using image information and partial least squares method to estimate mineral concentrations in mineral flotation". Proceedings of the Second International Conference on Processing and Manufacturing Materials, Honolulu, USA (1999) 459-464.         [ Links ]
[11] JÄMSÄ-JOUNELA., S., POIKONEN, R. VATANSKI, N., RANTALA, A. "Level control strategies for flotation cells". Minerals Engineering 16(11) (2003), 1069-1074.         [ Links ]
[12] KAARTINEN, J., HÄTÖNEN, J., HYÖTYNIEMI, H., MIETTUNEN, J. "Machine vision-based control of zinc flotation - A case study". Control Engineering Practice 14 (2006) 1455-1466.         [ Links ]
[13] KÄMPJÄRVI, P., JÄMSÄ-JOUNELA., S. "Level control strategies for flotation cells". Minerals Engineering 16(11) (2003) 1061-1068.         [ Links ]
[14] MALDONADO M., SBARBARO, D., LIZAMA, E. "Optimal control of a rougher flotation process based on dynamic programming". Minerals Engineering 20(3) (2007) 221-232.         [ Links ]
[15] OSORIO, D., PÉREZ-CORREA, R., CIPRIANO, A. "Assessment of expert fuzzy controllers for conventional flotation plants". Minerals Engineering 12(11) (1999) 1327-1338.         [ Links ]
[16] PÉREZ-CORREA, R., GONZÁLEZ, G., CASALI, A., CIPRIANO A. "Dynamic modeling and advanced multivariable control of conventional flotation circuits". Minerals Engineering 11(4) (1998) 333-346.         [ Links ]
[17] SBARBARO, D., MALDONADO, CIPRIANO, A. "A two level hierarchical control structure for optimizing a rougher flotation circuit". Proceedings of the 17th IFAC International Symposium in Automation in Mining, Mineral and Metal Processing, Seoul, Korea (2008) 1018-1022.         [ Links ]
[18] STENLUND, B. MEDVEDEV, A. "Level control of cascade coupled flotation tanks". Control Engineering Practice (10) (2002) 443-448.         [ Links ]
[19] SUICHIES, M. "An implementation of generalized predictive control in a flotation plant". Control Engineering Practice 8 (2000), 319-325.         [ Links ]
[20] ZAVALA, E., PÉREZ-CORREA, R., MUÑOZ, C., CIPRIANO, A. "Heuristic and model predictive control strategies for a simulated flotation circuit". Proceedings of the 8th IFAC International Symposium in Automation in Mining, Mineral and Metal Processing (1995) 59-64.         [ Links ]
[21] LIU, J., MACGREGOR, J. "Froth-based modeling and control of flotation processes". Minerals Engineering 21(9) (2007) 642-651.         [ Links ]